基于深度學習的FDA-MIMO雷達協方差矩陣缺失數據恢復方法

丁梓航 謝軍偉 王 博

①(空軍工程大學防空反導學院 西安 710051)

②(空軍工程大學空管領航學院 西安 710051)

1 引言

頻控陣(Frequency-Diverse Array,FDA)雷達因其在發射陣列中的各個陣元間增加了一個微小的頻偏而產生了距離-角度-時間三維相關的波束[1]，相較于常規的相控陣雷達，頻控陣雷達具有更加靈活的波束調控方式。因此，頻控陣雷達這一概念自2006年被提出后[2]，便受到了廣泛的關注和研究[3–6]。但頻控陣雷達的發射能量在空間中的分布隨時間變化，這一特性導致其發射波束能量無法長時間聚焦于某個空域位置。

為了解決頻控陣雷達波束的時變性問題，一種頻控陣與多輸入多輸出(Multi-Input and Multi-Output,MIMO)技術相結合的雷達體制被提出[7]，該體制不僅會消除波束的時間相關性還能夠實現波束在角度和距離維度上的解耦合。因此，FDA-MIMO雷達具有角度-距離相關的波束性能，且通過MIMO技術擴展了該雷達系統的自由度，使其能夠在多個雷達應用領域發揮一定的優勢，如包絡距離-角度聯合估計[8,9]、有源干擾壓制[10–13]、目標檢測與跟蹤[14–16]、空時自適應處理[17–20]等。

面對日益復雜的電磁環境，有源干擾信號給雷達系統帶來了巨大的挑戰。基于FDA-MIMO雷達的自適應波束形成算法能夠有效地壓制空域內的有源干擾信號[10–12,21,22]。這些波束形成算法的實現都依賴于采集到的干擾信號協方差矩陣，因此協方差矩陣數據不完整或者缺失時，會嚴重削弱雷達系統的波束形成效果和抗有源干擾能力。而協方差矩陣數據缺失現象主要原因來自以下兩個方面：

(1) 當雷達接收系統對回波信息進行采樣時，內部的存儲設備容易受到工作條件、電磁干擾和內部器件老化的影響，從而使得采集得到協方差矩陣內的數據與真實數據存在偏差甚至造成數據的缺失；

(2) 接收陣元通道中的器件產生的噪聲信號，以及模數轉換器等發生故障，導致部分通道無法正常工作，從而造成采集協方差矩陣數據的缺失。

針對矩陣數據缺失的補全問題，很多文獻采取添加合理性判斷條件的方式以保證數據恢復的可信性。一種基于最大期望(Expectation-Maximization,EM)算法的求解技術被廣泛應用于矩陣缺失數據恢復中[23,24]。文獻[25]提出了一種利用雜波協方差矩陣的結構特點，通過改進的EM算法實現對協方差矩陣數據的恢復，并將這一技術應用于波束形成和目標信號檢測。文獻[26]提出了針對不同缺失條件矩陣的無偏協方差估計器，并推導了對應的誤差界限。一種基于不完整數據條件下穩健的低秩協方差矩陣估計方法被提出[27]，該方法主要利用EM算法和矩陣特征值分解來實現低秩協方差矩陣數據的恢復。Xu等人[28]利用遷移學習網絡實現了步進頻雷達缺失信號數據的恢復。以上研究主要集中在利用合理性判斷條件和協方差矩陣結構特點來實現對缺失數據的補全。文獻[29]利用先驗數據及經驗結合深度神經網絡以實現數據的恢復。但利用深度學習來實現協方差矩陣缺失條件下的自適應波束形成的研究仍比較匱乏。

近年來，深度學習被應用于雷達的多個領域，與傳統算法相比，一定程度上提升了雷達的工作性能。文獻[30–32]提出了基于全連接網絡的波束形成算法，將協方差矩陣作為網絡的輸入，波束形成矢量作為網絡的輸出。此外，文獻[33]提出了一種基于卷積神經網絡的波束形成算法，實驗表明該網絡形成波束的性能優于常規的全連接網絡。但以上研究內容均是在已知完整的協方差矩陣基礎上實現波束形成，并沒有考慮協方差矩陣數據缺失的情形。

基于以上分析，本文主要研究了基于隨機缺失的FDA-MIMO雷達干擾加噪聲協方差矩陣的數據恢復問題，并在此基礎上構建了協方差矩陣恢復-自適應波束形成的抗有源干擾框架。首先建立雙通道生成對抗網絡(Generative Adversarial Network,GAN)，利用先驗協方差數據對該網絡進行訓練，以實現缺失協方差矩陣數據實部和虛部的同時恢復。在完成協方差矩陣數據恢復后，利用自適應波束形成算法對FDA-MIMO雷達波束進行優化，以實現對有源干擾信號的壓制，提升雷達系統的抗干擾能力。本文的主要工作和創新點體現在以下3個方面：

(1) 提出了一種基于深度學習的FDA-MIMO雷達干擾加噪聲協方差矩陣數據恢復算法；

(2) 建立了雙通道GAN網絡，通過構建兩個相互獨立且結構相同的網絡，分別對協方差矩陣數據的實部和虛部進行恢復，從而實現了干擾加噪聲協方差矩陣缺失數據的恢復；

(3) 本文所提方法在不同的數據損失率條件下均能夠實現矩陣數據的高精度恢復。

2 數據模型

2.1 FDA-MIMO雷達信號模型

考慮一個發射和接收陣列均為均勻線性陣列的收發共置FDA-MIMO雷達。其中，該雷達發射陣列含有M個發射陣元，接收陣列包含N個接收陣元，相鄰陣元間距為d=λ/2(λ為波長)。

在FDA-MIMO雷達的發射陣列中，設置相鄰發射陣元之間的頻率增量為?f，則第m個發射陣元的總頻率可以表示為

其中，f0表示發射陣元的載波頻率。若第m個發射陣元的基帶信號為φm(t)，則第m個陣元的發射信號表達式為

Et為陣列信號發射總能量，T表示雷達脈沖持續時間。基帶信號φm(t)滿足正交條件：

其中，(·)?表示共軛操作。

假設空間中的遠場目標位于(θ,r)，經過目標反射，第n個接收陣元接收到來自第m個發射陣元發射的信號表達式為

其中，α表示目標復反射系數(由信號發射幅度、相位、目標反射系數、傳播路徑衰減等組成)，τm,n表示從第m個發射陣元到第n個接收陣元之間往返信號的時延，其表達式為

其中，c 表示電磁波傳播速度，τ0=2r/c。

在窄帶信號假設下，存在近似關系φm(tτm,n)≈φm(t-τ0)。基于以上分析，第n個接收陣元接收到目標回波信號的表達式為

當發射頻偏大小滿足M?f ?f0時，式(6)中的近似關系成立。

信號被雷達接收系統接收后，會經過一系列的信號處理過程。本文采用文獻[34]提出的一種基于多匹配濾波器的FDA-MIMO雷達的接收處理系統。當接收陣元接收到目標反射信號后，首先需要經過混頻處理，即將接收信號與e-j2πf0t混頻，得到：

其中，α0=αej2πf0τ0。接下來，將每一個接收通道的信號分別輸入M組匹配濾波器通道中進行處理。在第l個匹配濾波通道，接收信號首先在數字端與ej2π(l-1)?ft(l=1,2,...,M)進行混頻，然后將混頻后的信號與(t)進行匹配濾波，獲得第l個匹配濾波通道的輸出結果

將式(7)代入式(8)，得到：

將N個接收通道分別經過M組匹配濾波器處理后得到的輸出信號排列成一個MN ×1維的列向量

其中，a(θ,r)=ar(θ)?a1(θ,r)

2.2 干擾加噪聲協方差矩陣構造及波束形成算法

本節主要介紹FDA-MIMO雷達接收干擾加噪聲信號協方差矩陣的構造方法以及基于最小均方無畸變響應(Minimum Variance Distortionless Response,MVDR)的最優接收濾波器的設計方法。最優濾波器設計方法用來評估協方差矩陣的恢復。

假設空間中存在多個有源干擾信號，且分別位于空間位置(θp,rp) (p=1,2,...,P)，則FDA-MIMO雷達接收到的干擾加噪聲信號可以表示為

其中，αp表示第p個干擾信號的幅度，P為干擾信號總數。接收信號協方差矩陣可以表示為

其中，E{·}表示求取期望操作，(·)H表示共軛轉置操作。定義第p個干擾信號的干噪比(Interferenceto-Noise Ratio,INR)為/。

設置波束指向的期望方向和距離分別為(θ0,r0)，接收濾波器矢量為w ∈CMN，自適應波束優化問題可以描述為

采用經典的MVDR算法[35]，得到最優接收濾波器矢量

其中，(·)-1表示矩陣求逆操作。

在式(19)的基礎上，雷達系統接收信干噪比(Signal-to-Interference-plus-Noise Ratio,SINR)可以表示為

從式(20)可以看出，雷達接收SINR性能與干擾加噪聲協方差矩陣相關，若干擾加噪聲協方差矩陣出現數據缺失的情況，將極大程度影響接收SINR性能，引起雷達系統的抗干擾能力下降等諸多問題。因此，如何有效地對信號協方差矩陣缺失數據進行精準的恢復對于雷達系統穩定工作是至關重要的。

3 數據缺失機制及網絡框架構建原理

本節主要介紹了數據隨機缺失機制下基于雙通道GAN網絡的矩陣數據恢復方法。在網絡中引入生成器(G)和鑒別器(D)兩種網絡，通過兩個網絡之間的相互對抗來實現對矩陣缺失數據的恢復。特別地，在網絡構建中，考慮到協方差矩陣為復數矩陣，本文構造了兩個具有相同結構的網絡，分別實現矩陣缺失數據實部和虛部的有效恢復。

3.1 數據隨機缺失機制

考慮到雷達協方差矩陣數據丟失的隨機性，本文假設協方差矩陣滿足隨機缺失規則，即矩陣中的所有位置的元素都擁有同樣的缺失概率，該缺失機制的數學描述如下：

根據第2節對FDA-MIMO接收干擾信號協方差矩陣的建模，該協方差矩陣的維度為MN ×MN，并將協方差矩陣Rin拉伸排列成一個(MN)2維的向量，該向量表示為x=[x1,x2,...,。設置一個維度同為(MN)2的掩碼向量m=[m1,m2,...,，其中mk ∈{0,1},k=1,2,...,(MN)2服從0-1分布，且mk=0的概率為ε(ε即為數據損失概率)。若mk=0，表示xd處的數據出現缺失，反之則表示該處數據被完整保留。定義一個新的向量?x來表示x出現數據缺失后的數據向量，該向量中的元素可以被描述為

數據恢復的目的是找到數據缺失的位置并將該位置的數據恢復到和原始矩陣相一致，即將完全恢復成x。為了實現該目標，受到基于深度學習的圖像恢復方法的啟發，本文提出了一種雙通道GAN網絡來實現對協方差矩陣缺失復數數據的恢復。

3.2 雙通道GAN網絡框架與原理

本節描述了雙通道GAN網絡框架的組成部分，并對網絡中的各個組成部分的作用及原理進行了解釋和分析。FDA-MIMO雷達信號協方差矩陣中的數據均為復數類型，因此本文在GAN網絡的基礎上增加了一個通道以實現對數據實部和虛部共同處理，整體網絡框架如圖1所示。

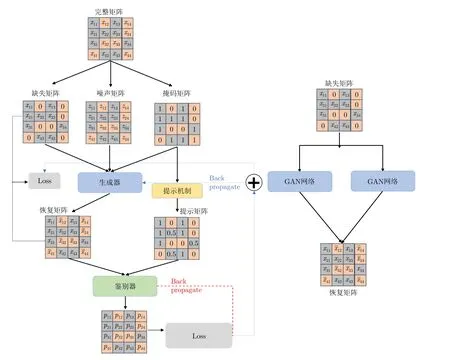
圖1 雙通道GAN網絡的框架Fig.1 The framework of dual channel GAN network

通過網絡的整體框架可以觀察到，雙通道網絡結構建立在常規GAN網絡的基礎上，分別引入了兩個相同的生成器G和鑒別器D，其分別用于數據實部和虛部的產生。下面對網絡框架中的各個組成部分的功能和原理進行詳細的分析。

A.生成器(Generator)

生成器網絡的輸入由矩陣缺失后的數據，掩碼向量m，以及設置的擾動向量z∈C(MN)2這幾部分組成，輸出為一個(MN)2維的向量。令生成器網絡函數為G，則生成器網絡的輸出xˉ可以表示為

在網絡完成訓練后，通過式(23)實現對缺失數據矩陣的恢復。

B.鑒別器(Discriminator)

在GAN網絡中，鑒別器是通過作為生成器的對手來實現對生成器網絡的訓練。而在所提網絡的框架中，D網絡并不是像常規的GAN網絡只需要判斷生成器的輸出結果是完全正確的或者是完全錯誤的，而是需要鑒別在輸出向量每個位置的真假，即輸出預測的掩碼向量。

設置鑒別器網絡函數為D，整個網絡可以表示為如下形式

其中，h為一種提示機制(Hint)生成的向量，下一部分將對網絡中的提示機制進行介紹。

C.提示機制(Hint)

引入提示機制的目的是強化生成器和鑒別器的對抗過程。向量h是由m經過人為設置的變換策略所得到的，將其作為鑒別器的一項擴展輸入，以實現對鑒別器的訓練。

h的選擇需要遵守一定的法則，文獻[36]提出了一種關于h的有效設計方法，該方法的數學描述為

D.網絡訓練目標

整個網絡框架中，通過最大化和最小化預測掩碼向量的正確率分別實現D網絡和G網絡的訓練。定義函數V(D,G)

其中，log(·)表示取以2為底的對數操作，是由G網絡輸出得到的。

GAN網絡的訓練目標可以被描述成一個minmax優化問題

定義損失函數

ai,bi分別表示a和b中的第i個元素。式(27)可以重新表示為

4 矩陣數據恢復算法

對式(29)中描述的min-max優化問題通過迭代的方法進行求解[36]。需要強調的是，生成器G和鑒別器D網絡的結構均為全連接神經網絡。兩個網絡的迭代訓練過程如下：

首先固定生成器G，對鑒別器D采用小批量數據(一個批次的樣本數量為JD)進行訓練，定義損失函數

在一個訓練批量中，D網絡參數訓練過程可以被描述為求解以下優化問題

m(j),(j),b(j)表示在一個批次中的第j個樣本，且(j)=D((j),h(j))。

當D完成一個批次的訓練時，固定D網絡的參數，隨機抽取樣本數量為JG的小批量數據對G網絡進行訓練。為了提高G網絡的訓練效率，定義兩種不同的損失函數，其中第1種的表達式為

第2種損失函數的表達式為

從兩種損失函數的定義表達式可以看出，LG是用來表征數據缺失部分，在mi=0的條件下，i的取值越接近于1，則LG的值越小。LM則是用于表征可觀測數據部分，G網絡的輸出越接近于矩陣觀測值，LM的值越小。因此，通過最小化兩種損失函數的線性組合以實現對G網絡的訓練，該優化問題可以表示為

其中，β為一個取值大于0的系數。

雙通道GAN網絡中的兩組鑒別器和生成器均采用以上步驟來完成網絡的訓練，且二者的訓練過程是相互獨立的，整個算法的偽代碼如算法1所示。

算法1 雙通道GAN偽代碼Alg.1 Pseudocode of dual channels GAN network

其中，Re(·),Im(·)分別表示取數據實部和虛部操作。

5 仿真分析

本節利用數值仿真驗證了所提FDA-MIMO雷達干擾加噪聲協方差矩陣缺失數據恢復方法的有效性。主要內容包括數據集(訓練集和測試集)的構建，雙通道GAN網絡對信號協方差矩陣的恢復效果分析，不同數據損失率及網絡層數對所提算法性能的影響，以及協方差矩陣恢復前后的波束形成性能比較，不同缺失數據恢復方法性能比較等方面進行仿真實驗。在雙通道GAN中，兩個獨立通道的網絡結構始終保持一致。其中，鑒別器和生成器網絡均為全連接神經網絡，上述兩種網絡的具體結構如圖2所示，均為6層全連接網絡。本文使用深度學習環境Pytorch1.9對雙通道GAN網絡進行搭建和訓練。

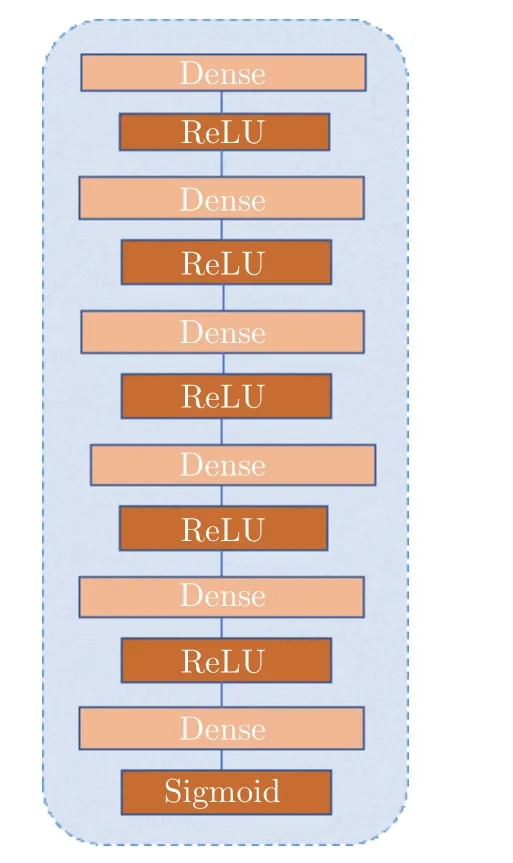
圖2 鑒別器和生成器網絡結構Fig.2 The structure of D and G network

5.1 數據集(訓練集和測試集)構建方法

本節介紹了網絡訓練所需數據集的構建方法。在數值仿真中，FDA-MIMO雷達的參數設置情況如下：發射陣元和接收陣元數量分別為M=8和N=6，發射頻偏采用線性頻偏樣式，且相鄰陣元間頻偏為?f=6 kHz，發射和接收陣列中的陣元間距均等于半波長寬度。

設置干擾信號源個數1，干噪比(INR)為5 dB。干擾信號源在空間中的角度變化范圍為[20?,50?]，角度間隔為 5?。干擾信號距離變化范圍是[20 km,50 km]，間隔為5 km。利用2.2節提出的干擾加噪聲協方差矩陣的構造方法，獲得來自不同角度和距離的干擾加噪聲信號的協方差矩陣數據(總計49個維度為MN ×MN的協方差矩陣)，并將每一個空間位置對應的協方差矩陣復制300份，得到由(49×300)個協方差矩陣構成的數據集。為了適應網絡輸入，每一個協方差矩陣都將轉化為1×M2N2的向量。因此，整個數據集的維度變為(49×300)×M2N2。接下來按照訓練集:測試集等于4:1的配比，分別對訓練集和測試集進行劃分，完成數據集的構建。需要說明的是，當該數據集用于網絡訓練時，需要對數據進行規范化處理，即將數據均映射到[0,1]取值區間內。由于G網絡和D網絡均為全連接神經網絡，因此其網絡的計算復雜度可以分別表示為BG=O(NInputGN1+N1N2+N2N3+N3N4+N4NOutputG),BD=O(NInputDN1+N1N2+N2N3+N3N4+N4NOutputD)，則所提雙通道GAN網絡總的計算復雜度為O(2BG+2BD)，其中NInputG,NOutputG表示G網絡的輸入和輸出數據維度，NInputD,NOutputD表示D網絡的輸入和輸出數據維度。Ni(i=1,2,3,4)表示第i層的神經元個數。

5.2 協方差矩陣恢復效果分析

雙通道網絡訓練參數設置情況如下：矩陣數據丟失率ε=0.3，一個批次中的樣本數為JD=JG=128，訓練過程中的迭代次數為10000，兩個網絡的學習率均設置為0.001。

當雙通道GAN網絡完成訓練后，為了驗證所提矩陣缺失數據恢復方法的有效性，隨機選擇測試集中的一組協方差矩陣數據(該樣本對應干擾信號的距離和角度分別為35 km,45?)，利用經過訓練的雙通道GAN網絡對該協方差矩陣的缺失數據進行恢復。完整的協方差矩陣，缺失后的協方差矩陣，未經過訓練網絡輸出的恢復矩陣，完成訓練后網絡輸出的恢復矩陣等4種矩陣的實部和虛部對應的灰度圖如圖3和圖4所示。

圖3 協方差矩陣實部灰度圖(單干擾源)Fig.3 The grayscale image of the real part of covariance matrix (single interference)

從圖3和圖4矩陣實部和虛部的灰度圖可以看出，矩陣數據的缺失破壞了干擾加噪聲協方差矩陣數據的結構，對雷達系統后續的處理造成很大的麻煩，影響雷達系統的工作性能。經過訓練后的雙通道GAN網絡能夠有效地對FDA-MIMO雷達干擾加噪聲協方差矩陣數據進行恢復，且恢復程度較高，而未經過訓練的網絡的恢復效果較差，仍包含較多缺失數據。

5.3 不同數據損失率及網絡層數對所提算法性能的影響

在所提矩陣數據恢復方法有效性被驗證的基礎上中，本節主要分析了不同數據損失率ε以及網絡層數k的變化對矩陣缺失數據恢復性能的影響。仿真參數與5.2節一致。為了定量地評估矩陣數據恢復性能，引入均方根誤差(Root Mean Squared Error,RMSE)，其表達式為

設置網絡層數為6，圖5表示數據損失率分別在ε=0.2,0.3,0.4,0.5的4種情況下，網絡訓練過程中矩陣數據恢復的RMSE變化情況。從圖5可以看出，對于4種不同的損失率，所提算法均能夠有效地實現網絡訓練的收斂，且具有幾乎相同的收斂速度，當網絡訓練達到收斂時，ε=0.5對應的矩陣數據恢復的RMSE最大。

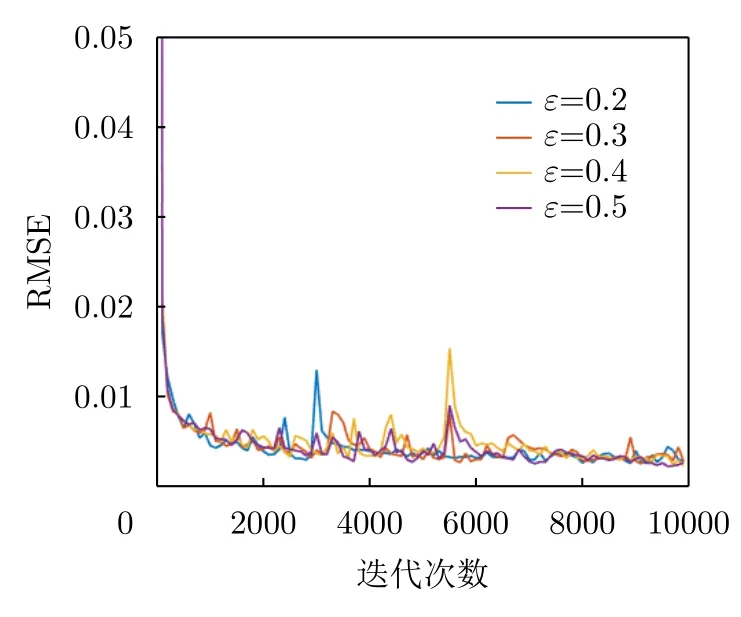
圖5 矩陣恢復數據的RMSE在訓練過程中的變化情況(不同損失率 ε)Fig.5 RMSE performance versus training process (different ε)

此外，為了定量地描述不同損失率對矩陣數據恢復算法性能的影響，將測試集中的所有樣本輸入到訓練完成后的雙通道GAN網絡中，計算整個測試集對應矩陣恢復數據的平均RMSE。不同數據損失率對應的RMSE結果如表1所示。隨著數據損失率的提高，所提矩陣數據恢復算法的性能將會出現一定程度的下降。盡管如此，所提方法仍能夠將協方差矩陣恢復數據的誤差控制在精度為1E–02的范圍內，該結果同時也驗證了所提算法的魯棒性。

表1 測試集矩陣恢復數據的平均RMSE(不同損失率 ε)Tab.1 Average RMSE of the missing data recovery (different ε)

G和D網絡結構在一定程度上將對矩陣數據恢復性能產生影響，因此考慮不同的網絡層數(k=3,6,9)對網絡訓練過程和矩陣恢復表現的影響。矩陣恢復數據的RMSE在訓練過程中的變化情況如圖6所示。在訓練開始階段，相較于3層神經網絡結構，6層和9層網絡可以在一定程度上提高訓練的收斂速度。

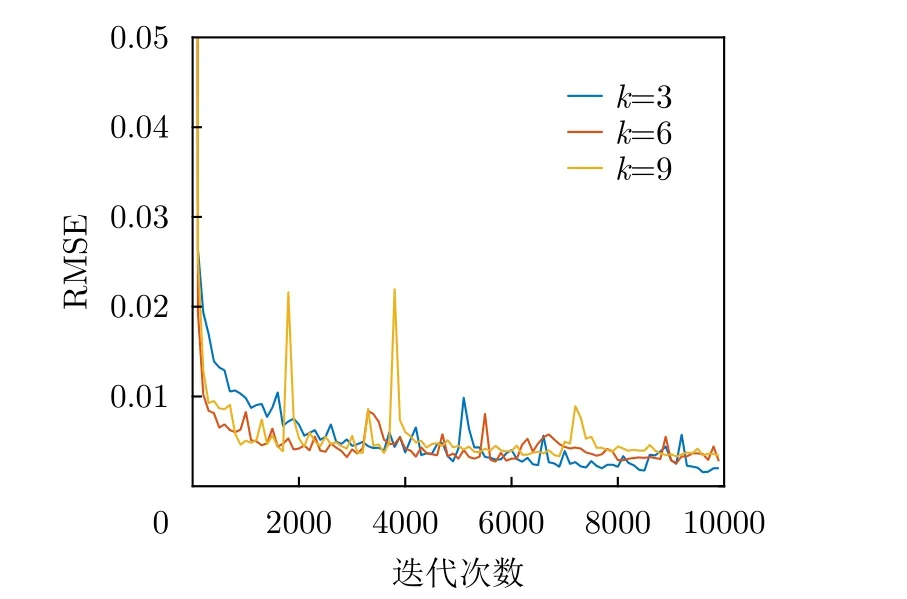
圖6 矩陣恢復數據的RMSE在訓練過程中的變化情況(不同網絡層數k)Fig.6 RMSE performance versus training process (different k)

3種結構的網絡完成訓練后，通過測試集對網絡的數據恢復性能進行評估，評估結果如表2所示。從3種網絡對應的測試集平均RMSE表現可以看出，相較于k=3,9，當k=6時，整個網絡能夠獲得最優的恢復性能，而k=3對應網絡的數據恢復性能最差。因此，需合理選取全連接網絡的層數，以獲得較好的訓練性能。

表2 測試集矩陣恢復數據的平均RMSE(不同網絡層數k)Tab.2 Average RMSE of the missing data recovery (different k)

以上仿真結果表明，所提算法通過合理設置網絡參數和結構能夠高精度地完成協方差矩陣缺失數據的恢復和補全。為了進一步闡明所提算法的優勢，分別引入EM算法[25]、隨機森林[37]、降噪自編碼器[29]等3種已被提出的缺失數據恢復方法，比較4種不同方法對缺失數據的恢復精度。利用不同方法對測試集數據進行恢復得到的平均RMSE結果如表3所示。

表3 測試集矩陣恢復數據的平均RMSE(不同方法)Tab.3 Average RMSE of the missing data recovery(different methods)

從表3結果可以看出，本文所提算法相較于其他3種方法具有明顯的缺失數據補全精度優勢，驗證了雙通道GAN網絡對缺失數據恢復的有效性。

5.4 協方差矩陣恢復前后的波束形成性能比較

協方差矩陣數據的缺失會對整個協方差的結構造成很大程度的影響，直接導致自適應波束形成算法無法準確地形成期望的波束。為了驗證所提方法對協方差矩陣的恢復效果以及FDA-MIMO雷達波束形成的性能的影響，本節重點對利用恢復后的干擾加噪聲協方差矩陣形成的波束性能進行仿真分析。仿真參數的設置與5.2節相同，設置目標信號在空間中的位置為(20?,30 km)，選取測試集中的一個樣本，該樣本對應干擾信號的空間位置為(45?,35 km)。利用2.2節所述的自適應波束形成算法，分別得到完整協方差矩陣、缺失協方差矩陣和恢復后協方差矩陣對應的FDA-MIMO雷達波束方向圖，上述3種波束方向圖如圖7所示。從仿真結果可以看出，完整協方差矩陣和恢復協方差矩陣對應形成的波束方向圖十分接近，且均能夠在干擾信號位置形成穩定的零陷，而缺失協方差矩陣對應的波束方向圖相較于其他兩種協方差矩陣產生了巨大的畸變，且無法在干擾信號位置形成有效的零陷。此外，利用完整協方差矩陣和恢復協方差矩陣得到的SINR值分別為–39.67 dB,–39.06 dB，這一結果表明本文所提算法能夠對FDA-MIMO雷達缺失信號協方差矩陣進行高精度的恢復，且極大程度保留了FDAMIMO雷達的抗干擾性能。

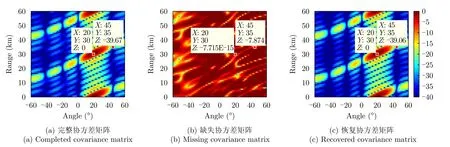
圖7 基于不同協方差矩陣的FDA-MIMO雷達波束方向圖(多干擾源)Fig.7 FDA-MIMO radar beampattern based on different covariance matrices (single interference)

5.5 多干擾源信號協方差矩陣恢復性能分析

為了驗證所提雙通道GAN網絡對多干擾信號協方差矩陣缺失數據的恢復效果，本節引入兩個位于不同空域位置的干擾信號，利用所提網絡實現對兩干擾信號的協方差矩陣進行缺失數據恢復。

首先對數據集進行構建，構建方法與5.1節類似，設置兩個干擾源信號，干擾信號1在空間中的角度變化范圍為[20?,50?]，間隔為5°，距離變化范圍是[10 km,50 km]，間隔為5 km，干噪比變化范圍為[0 dB,10 dB]，間隔為2 dB。干擾信號2在空間中的角度變化范圍為[0?,15?]，間隔為5°，距離變化范圍是[60 km,80 km]，間隔為5 km，干噪比變化范圍為[0 dB,10 dB]，間隔為2 dB。

網絡完成訓練后，隨機選擇測試集中的一組協方差矩陣數據，其中干擾信號1在空間中的位置為(20?,10 km)，干擾信號2在空間中的位置為(10?,60 km)。完整的協方差矩陣，缺失后的協方差矩陣，未經過訓練網絡輸出的恢復矩陣以及完成訓練后網絡輸出的恢復矩陣等4種矩陣的實部和虛部對應的灰度圖如圖8和圖9所示。

圖9 協方差矩陣虛部灰度圖(多干擾源)Fig.9 The grayscale image of the imaginary part of covariance matrix (multiple interferences)

以上仿真結果驗證了所提網絡能夠對多干擾信號形成的協方差矩陣缺失數據進行有效的恢復。接下來，為了進一步評估所提方法對干擾加噪聲協方差矩陣的恢復效果，設置目標信號的空間位置為(20?,30 km)。利用2.2節所述的自適應波束形成算法，分別得到完整協方差矩陣、缺失協方差矩陣和恢復后協方差矩陣對應的FDA-MIMO雷達波束方向圖，上述3種波束方向圖如圖10所示。從3個不同的波束方向圖可以看出，經過所提方法對協方差矩陣補全后的波束性能與完整協方差矩陣基本一致，且對兩個干擾位置的幅度波動均在1 dB以內，驗證了所提方法能夠有效保持在協方差矩陣出現數據缺失情況下的波束形成性能。

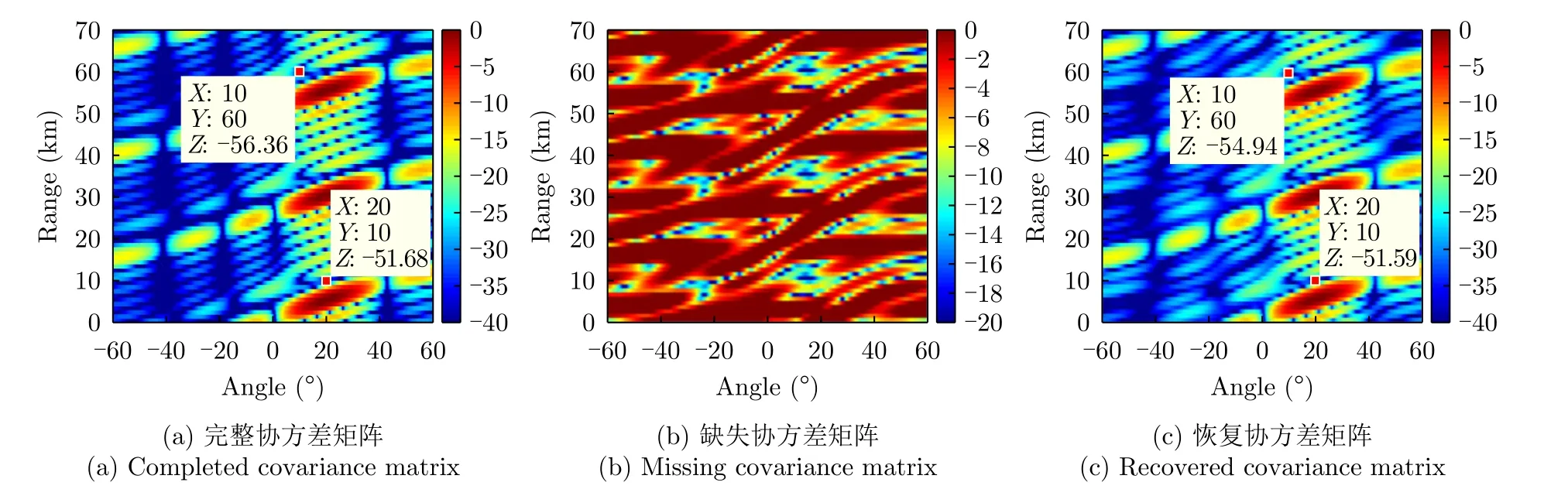
圖10 基于不同協方差矩陣的FDA-MIMO雷達波束方向圖(多干擾源)Fig.10 FDA-MIMO radar beampattern based on different covariance matrices (multiple interferences)

6 結語

本文提出了一種基于雙通道GAN網絡的FDAMIMO干擾加噪聲協方差矩陣數據恢復方法。雙通道GAN網絡能夠同時實現矩陣缺失數據實部和虛部的恢復。通過合理設計鑒別器和生成器網絡的損失函數，實現兩個網絡之間在訓練過程中的相互對抗，從而完成整個網絡的訓練。在此基礎上，引入一種提示機制，用于提高鑒別器網絡的訓練效果。在數值仿真中，經過訓練后的雙通道GAN網絡能夠有效地對缺失協方差矩陣數據的實部和虛部進行恢復。此外，該算法也適用于對不同數據損失率，且能夠將矩陣數據恢復精度控制在1E–02的量級內。本文還研究了鑒別器和生成器網絡的層數對網絡訓練結果的影響，通過比較網絡層數為3層、6層和9層3種結構，發現選擇6層的網絡結構獲得的訓練效果和矩陣數據恢復效果最優。在此基礎上還將已有缺失數據恢復方法與所提方法性能進行了比較。最后，利用自適應波束形成算法分別生成完整的協方差矩陣、缺失的協方差矩陣和恢復的協方差矩陣對應的二維波束圖，其中完整的協方差矩陣和恢復的協方差矩陣生成的波束方向圖幾乎相同，且SINR表現相差在1 dB的范圍內，驗證了本文所提矩陣數據恢復算法的有效性。