蜀南竹海大跨度人行懸索橋抗風性能分析

林智敏, 羅照鑫, 楊培森

(1.成都大學,四川成都 610106;2.四川西南交大土木工程設計有限公司,四川成都 610031)

1 橋梁概況

蜀南竹海作為4A級國家級風景名勝區,被評為中國最美的十大森林之一,但內部經營方式較單一,缺少特色體驗互動類型的旅游項目。根據景區發展需要,擬建設一座大跨度的人行懸索橋,增加游客的選擇性與趣味性。根據前期規劃及方案設計,橋梁選址距離景區游客中心約11 km,位于七彩飛瀑景區東北側,跨越深度約220 m的峽谷。

本橋采用雙索面地錨式懸索橋,主跨主纜跨度320 m,矢跨比1/10,主梁總長300 m,標準段寬度3 m。鋼箱梁采用分離式雙箱,通過橫隔梁形成縱橫相間的格子體系,上面鋪設鋼化玻璃。全橋設4個主塔,均為獨柱結構,下設樁基承臺。兩岸錨碇均為重力式錨碇[1](圖1)。

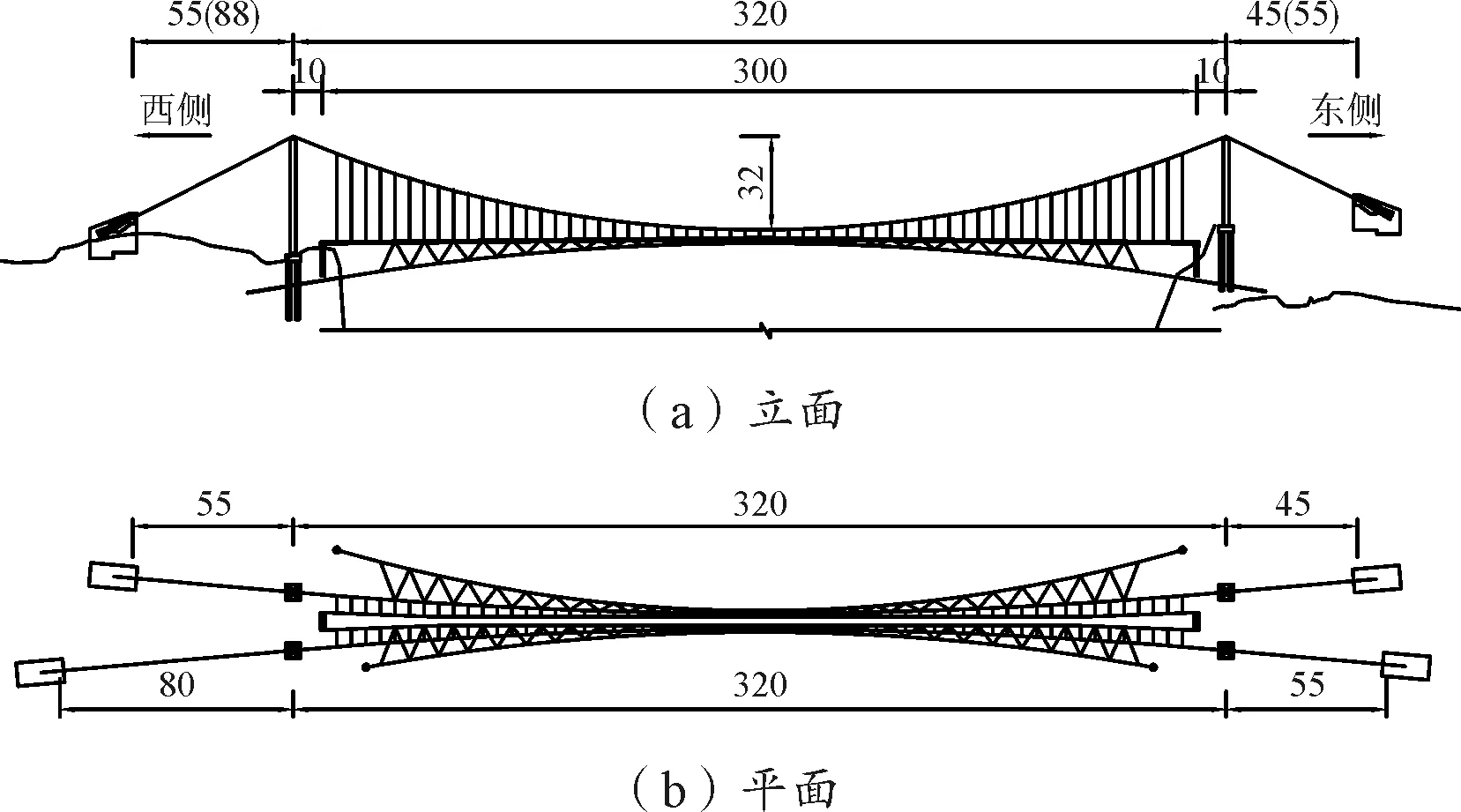
圖1 橋梁總體布置(單位:m)

由于本橋跨度大,寬度小,抗風穩定性問題較為突出。為提高橋梁的抗風性能:①主纜采用空間纜的布置形式,從跨中到邊跨逐步展開;②在橋梁兩側下方斜平面對稱布置抗風索;③主梁采用分離式鋼箱梁的形式,兩側設置風嘴。在采取了上述措施后,對橋梁的抗風性能進行計算分析,驗證其效果。

2 設計風參數的確定

橋位處于四川省長寧縣蜀南竹海景區,可以取周邊氣象站的參考數據,橋位距離宜賓氣象站較近,根據國家氣象資料,截止到2015年,可以推算到宜賓100年一遇基本風速為25.10 m/s。橋位地處山區峽谷,可以歸為D類地表,根據我國JTG/T 3360-01-2018《公路橋梁抗風設計規范》計算得到橋面設計基準風速為26.95 m/s,主梁成橋狀態顫振檢驗風速為53.42 m/s,主梁成橋狀態靜風穩定檢驗風速43.12 m/s。

3 結構動力特性計算分析

橋梁在風作用下的響應和橋梁的結構動力特性關系密切,因此結構動力特性是進行結構動力響應分析的前提。通過結構動力特性分析,可得到橋梁結構的頻率分布及振型特點,并為后續的抗風分析提供相應的計算基礎數據。在與橋跨垂直的橫向風的作用下,橋梁結構會在發生相應的平動和轉動,其位移方向體現出明顯的空間性。因此計算模型應采用三維模型,并準確地模擬橋梁剛度和質量的空間分布特點。

蜀南竹海人行懸索橋有限元模型采用雙主梁進行模擬,每隔5 m設置一道橫梁,吊桿連接點與主梁之間采用剛臂進行連接。主纜及吊桿采用空間桿單元。成橋狀態結構的邊界條件:

(1)主梁與橋臺部分,主梁豎向、橫橋向自由度均與橋臺變位主從,順橋向自由度放松。

(2)主纜及抗風索端部約束所有自由度。

(3)索塔底部約束所有自由度,不考慮樁土相互作用。

(4)主纜與索塔頂端連接部分,主纜順橋向、橫橋向、縱向均與索塔主從[2]。

各部分構成了蜀南竹海人行懸索橋結構有限元模型,整個模型共有409個節點,739個單元。圖2為采用ANSYS軟件建立的結構有限元模型。

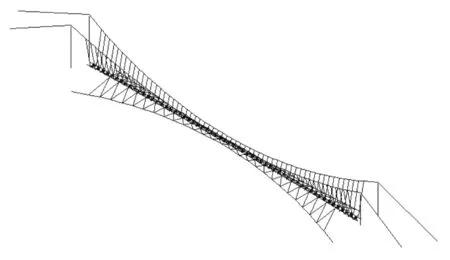
圖2 蜀南竹海人行懸索橋結構有限元離散

對蜀南竹海人行懸索橋進行成橋狀態下結構有限元模態分析,其主要自振頻率見表1。

表1 結構動力特性計算結果

橋梁一階豎彎及一階扭轉振型如圖3、圖4所示。

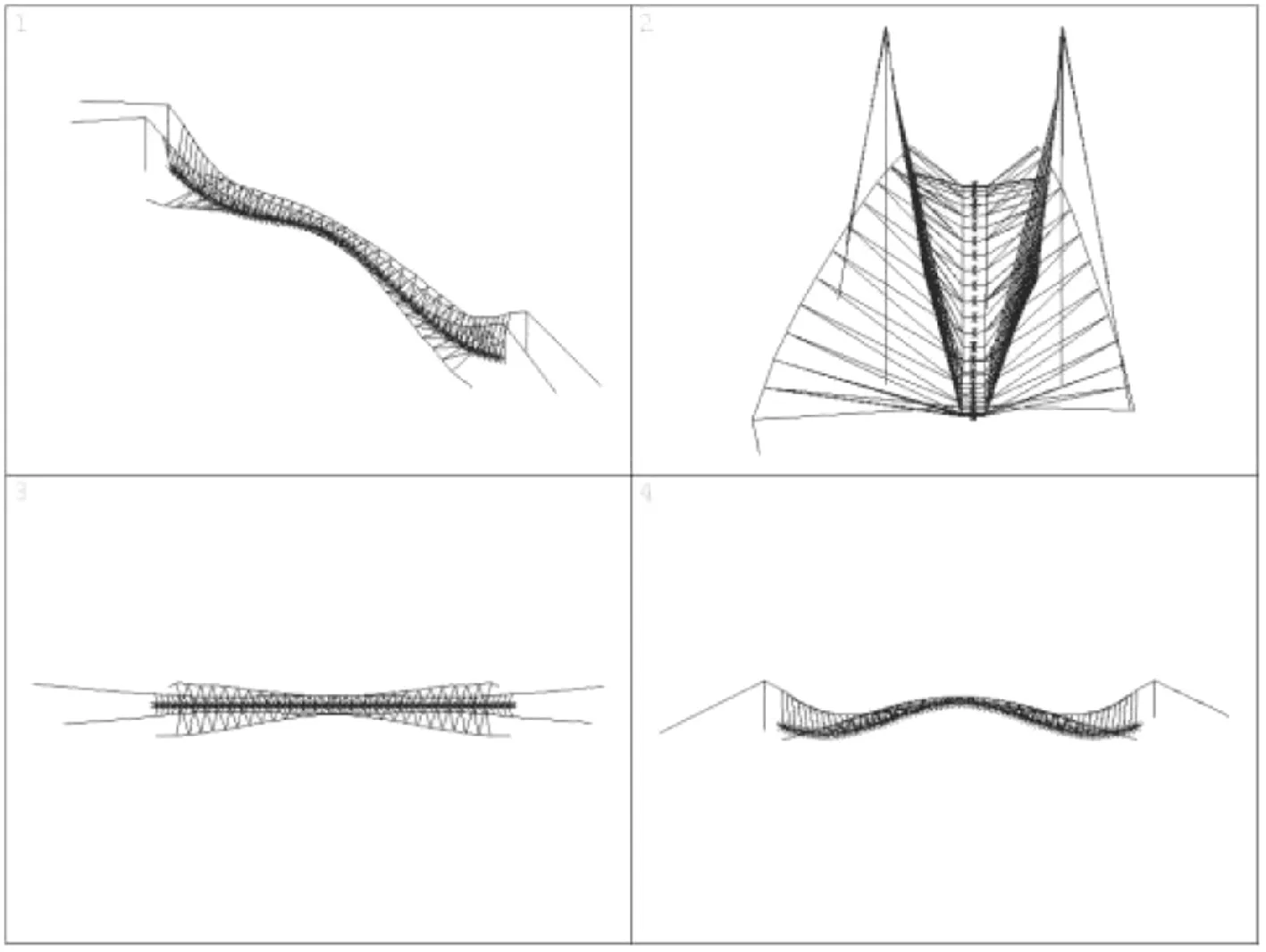
圖3 橋梁一階豎彎振型

圖4 橋梁一階扭轉振型

4 靜風穩定性分析

4.1 分析方法

橋梁結構的空氣靜力穩定性體現在兩方面,一方面考慮結構是否出現側向屈曲,另一方面考慮原結構是否扭轉發散。

當風速達到橋梁的空氣靜力失穩的臨界風速時,橋梁將產生失穩,因此導致災難性的后果。因此,對橋梁結構而言,靜風穩定性的要求表述為靜力失穩的臨界風速必須大于空氣靜力穩定性檢驗風速。

確定空氣靜力失穩臨界風速的方法有2種:全橋氣動彈性模型風洞試驗和基于靜力三分力系數的計算分析。通過全橋氣動彈性模型風洞試驗直接測量臨界風速的方法會造成模型損壞,通常不便于實施。基于靜力三分力系數的計算分析,傳統方法是基于線性理論,將側向屈曲和扭轉發散分別處理,得到的臨界風速值顯著高于真值。更為精確的方法是利用非線性有限元法對結構進行風荷載—位移非線性分析。實踐證明,這種方法具有良好的精度。因此采用該種方法進行分析。

進行非線性分析時,靜風荷載非線性是指靜風荷載作用隨著主梁斷面發生扭轉變形同步發生非線性變化的過程。隨著風速的增加,主梁將發生扭轉,結構的受力初始形態發生變化,三分力系數隨之改變,從而導致主梁上的靜風荷載發生變化。由此可見,作用于主梁上的靜風荷載是隨著主梁的位移變化而同步變化的。在進行計算分析時,應將主梁上的靜風荷載定義為以主梁位移為變量的函數[3]

在保證對結構進行合理的抽象和簡化的過程中準確反映結構質量和剛度的空間分布,以及保證所建立的邊界條件真實反映結構的工作行為的基礎上,建立三維計算模型,采用空間桿系來模擬結構行為。分析所用的計算模型及結構狀態與前面的結構動力特性分析所用者相同。

在計算發散風速時,首先假定一組基準風速,通過計算分析得到主纜拉力機主梁的扭轉角度,以此纜力及主纜扭轉角度作為新一級的初始狀態輸入模型,再重復上一次計算,反復迭代,直至模型發散為止。在計算過程中,應合理取用風速步長,以得到較為準確的計算結果。

4.2 分析結果

按照上述方法分別計算了蜀南竹海懸索橋成橋狀態0°風攻角下的靜風失穩臨界風速。圖5～圖7為0°攻角下,蜀南竹海懸索橋成橋狀態空氣靜力穩定性分析所得主梁跨中豎向位移、橫向位移及扭轉角隨風速變化情況。

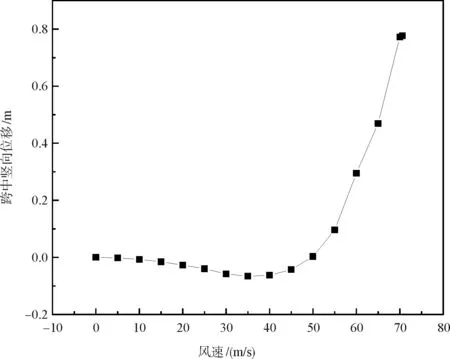
圖5 成橋狀態跨中豎向位移隨風速變化情況

圖6 成橋狀態跨中橫向位移隨風速變化情況

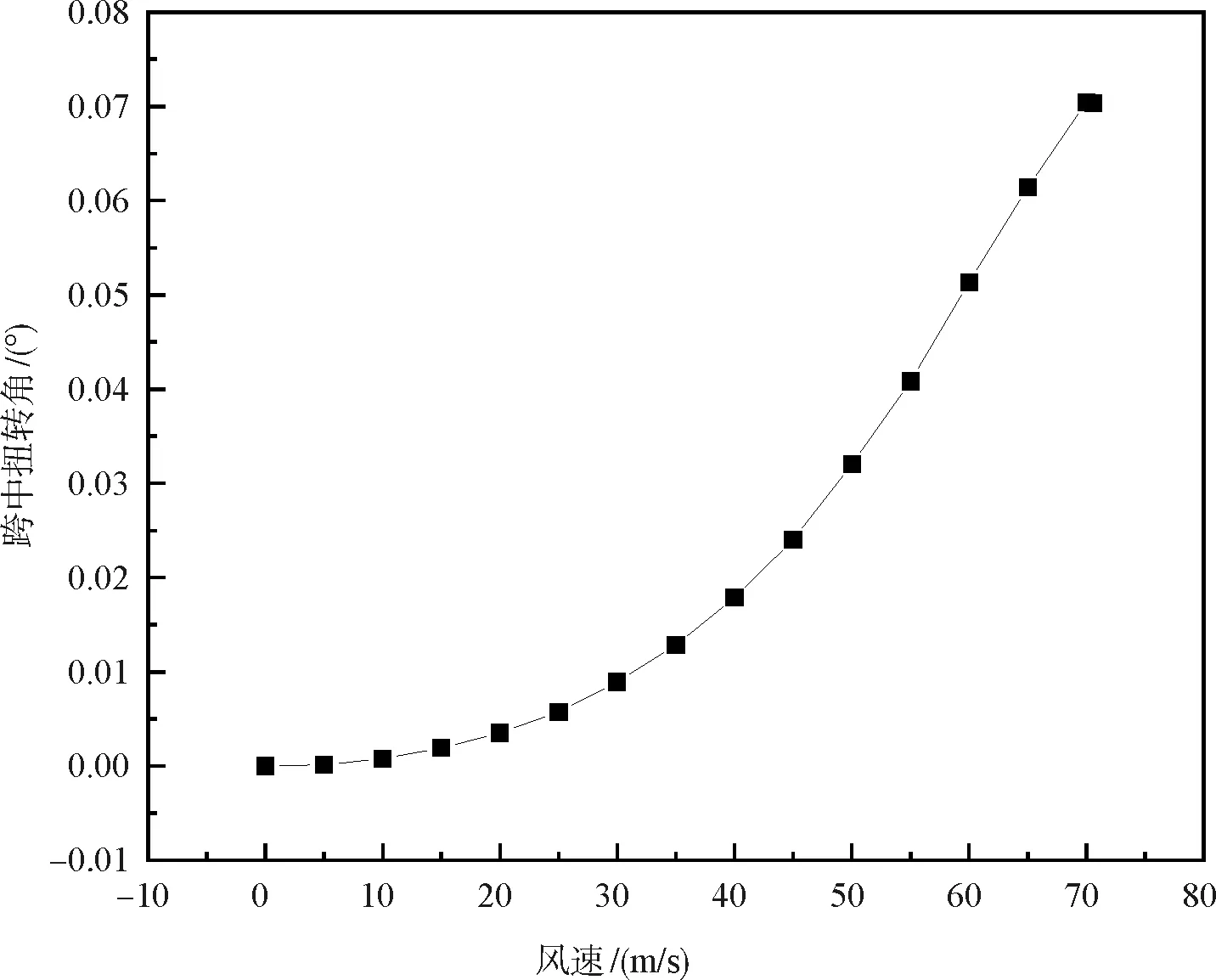
圖7 成橋狀態跨中扭轉角隨風速變化情況

計算所得蜀南竹海懸索橋成橋狀態的靜風臨界失穩風速為70.6 m/s,大于相應狀態的靜風失穩檢驗風速43.12 m/s,表明該橋的靜風穩定性滿足要求。

5 顫振穩定性分析

顫振是一種自發性的自激振動,主要是由于振動結構能夠在流動的空氣中不斷吸收能量,當橋梁所吸收的能量不能完全被結構本身的阻尼體系所消耗吸收,多余的能量會使橋梁結構的振幅逐漸增大最終引起橋梁的發散振動[4]。

本橋采用開口型的分離式雙箱斷面,這種斷面形式常用于大跨度的斜拉橋和懸索橋。但這種分離式雙箱截面氣動穩定性較差,而顫振對于主梁的氣動外形十分敏感,所以采用分離式雙箱截面的斜拉橋和懸索器常要采用額外的構造措施進行氣動性能優化。對于本橋而言,梁寬較窄,未增加額外的氣動性能優化構造措施,但必要的顫振穩定性分析必不可少[5]。

根據JTG/T 3360-01-2018《公路橋梁抗風設計規范》進行計算,橋梁的顫振臨界風速為58.56 m/s,高于53.42 m/s的顫振檢驗風速,因此橋梁顫振穩定性滿足要求。

6 渦激振動穩定性分析

渦激振動是大跨度橋梁在低風速下很容易出現的一種風致振動現象,其帶有自激性質,振動的結構反過來會對渦脫形成某種反饋作用,使得渦振振幅受到限制。來流經過橋梁斷面時,必然會發生繞流現象,其截面背后的周期性漩渦脫落將產生周期變化的作用力—渦激力。當被繞流的物體是一個振動體系時,周期性的渦激力將引起結構的渦激振動,并且在漩渦脫落頻率與結構的自振頻率一致時發生渦激共振[6]。

對于主梁,渦激振動形式主要表象為豎直方向的振動和扭轉振動。與顫振的發散性不同,渦激振動振幅有限,短時間不會對橋梁造成失穩的破壞性后果。但由于渦激振動具有時長較長的特點,對于橋梁上的行人會產生嚴重的不適感,更為嚴重的情況下甚至會導致鋼結構橋梁發生疲勞開裂。

按照JTG/T 3360-01-2018《公路橋梁抗風設計規范》對主梁的渦激振動特性作出評價。經計算,懸索橋的渦激振動性能如表2所示,結果表明蜀南竹海人行懸索橋渦激振動性能滿足規范要求[7]。

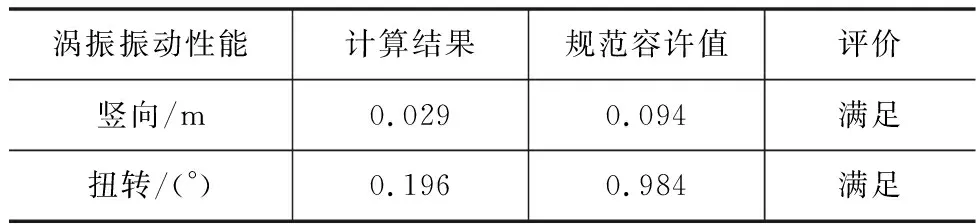
表2 成橋狀態渦激振動性能計算結果

7 結論

蜀南竹海人行懸索橋寬跨比極小,橋梁的抗風穩定性問題非常突出。經計算分析,橋梁的靜風穩定性、顫振穩定性及渦振穩定性均滿足使用要求,表明所采取的設置空間索、抗風索及分離式鋼箱等措施對改善本橋的抗風性能是有效的。