求解二階錐絕對值方程組的慣性two-sweep 迭代法

洪曉曼，唐嘉

（福建師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院，福建 福州 350007）

絕對值方程問題(AVE)是數(shù)學(xué)規(guī)劃中的一個重要的優(yōu)化問題。自從Rohn[1]于2004 年首次提出以來，此后便吸引大量的學(xué)者對其解的存在性理論、數(shù)值求解以其收斂性分析進行深入探究。目前已經(jīng)提出許多的數(shù)值求解方法，例如光滑牛頓法[2]、符號標記法[3]、松弛的非線性PHSS 類迭代法[4]等。近幾年一些學(xué)者將AVE的相關(guān)理論進行推廣，將AVE 延伸至二階錐的框架之下，提出二階錐絕對值方程（SOCAVE）問題：

式中：A∈Rn×n，b∈Rn和表示二階錐意義下的x 的絕對值(定義為x 與自身的若當乘積的二次方根)，x∈Kn。通常意義下的二階錐Kn是若干個二階錐的笛卡爾乘積:

式中：n1+n2+…+nr=n 且≤x1｝，‖·‖表示歐氏空間的2-范數(shù)，只考慮單個二階錐的情形即r=1。由于笛卡爾乘積的性質(zhì)，所有的分析同樣適用于多個二階錐的笛卡爾積的情形。

SOCAVE(1)對錐優(yōu)化這個新領(lǐng)域起到極其重要的作用。目前國內(nèi)的一些學(xué)者對SOCAVE(1)進行了相關(guān)研究，并提出很多求解SOCAVE(1)的數(shù)值方法。例如，Hu 等[5]提出求解SOCAVE(1)的廣義牛頓法，并證明該算法在一定條件下是全局收斂且局部二次收斂的。Miao 等[6]提出求解SOCAVE(1)的光滑牛頓法，證明該算法在一定條件下是局部二次收斂的。Huang 等[7]提出求解SOCAVE(1)的一種改進SOR-like 方法，在一定條件下對該算法進行收斂性分析和誤差估計。最后將該算法與二階錐上GN[5]、NSOR[8]、NINA[9]等方法進行對比，證明了所提出的迭代算法是有效的。

Zhang 等[10]在Li 研究的修正廣義牛頓迭代方法[11](MGNT)的啟發(fā)下,結(jié)合two-sweep 迭代方法[12-13]和單位矩陣方程[6，14]的思想，提出了求解AVE 的改進twosweep 迭代方法(MTS),將所提出的方法與MGNT 方法[11]和SOR-like 方法[15]進行一些數(shù)值實驗，實驗證明該方法在迭代步長和耗時方面更為有優(yōu)勢。基于此，將Zhang 等[10]的思路更進一步地擴展到求解SOCAVE(1)中去，添加一個慣性項(可見文獻[16])，提出了求解SOCAVE(1)的慣性two-sweep 迭代方法，將所提出的方法與GN 方法[5]和MSOR-like 方法[7]進行數(shù)值實驗對比，最后數(shù)值實驗證明所提出的方法可行且有效的。

其余部分組織如下：在第二節(jié)中，主要介紹本文研究內(nèi)容所涉及的基礎(chǔ)知識以及相關(guān)引理；在第三節(jié)中,我們提出了求解SOCAVE(1)的慣性two-sweep 迭代方法并分析了相應(yīng)算法的收斂性；在第四節(jié)中，給出所有相關(guān)算法的數(shù)值實驗結(jié)果；在第五節(jié)中，對本文的工作進行總結(jié)。

1 預(yù)備知識

在歐式空間Rn中，基于二階錐Kn，定義一個歐式若當代數(shù)V：＝（Rn,〈·,·〉,o），其中“o”表示若當乘積的運算符號，對于任意兩個向量x=（x1，x2）∈R×Rn-1和y=（y1，y2）∈R×Rn-1，它們的若當乘積定義為：

基于上述若當乘積的定義，可知該若當代數(shù)V 中存在的單位元e=（1，0，…，0）∈Rn，x2表示x 與自身的若當乘積，即x2=x o x，因此SOCAVE(1)中絕對值的定義為。對于任意向量x=（x1，x2）∈R×Rn-1，基于二階錐Kn的譜分解具有如下形式：

式中：λ1（x），λ2（x）稱為x 的特征值，為對應(yīng)的特征向量，它們的具體表達式如下：

式中：i=1,2,ω∈Rn-1,為滿足‖ω‖=1 的任意向量。這里稱為若當框架且有。如果x2≠0，則該譜分解表達式是唯一的。

令x+表示為x 在二階錐Kn上的投影，x-表示為-x 在二階錐Kn的對偶錐（Kn）*上的投影，結(jié)合x的譜分解(2)，可知x=x+-x-，基于文獻[9]，可知：

引理1[17]設(shè)矩陣A∈Rn×n是非奇異的，矩陣A的逆的二范數(shù)嚴格小于1，即‖A-1‖<1，則二階錐上的絕對值方程(1)對任意b∈Rn具有唯一解。

引理2[18]令

引理3[19]設(shè)向量x=（x1，x2），y=（y1，y2）∈R×Rn-1，那么

2 二階錐絕對值方程組的慣性two-sweep迭代法及其收斂性分析

在本節(jié)中，將重點討論和介紹二階錐絕對值方程組的慣性two-sweep 迭代法(ITSM) 及其收斂性分析。在此之前，首先回顧Zhang 等[18]的MTS 迭代法，該方法是結(jié)合two-sweep 迭代法和添加單位矩陣方程的思想，用于求解AVE。基于MTS 方法，我們在二階錐的框架之下，通過添加慣性項a（xn-xn-1），將所要求解的二階錐絕對值方程等價地轉(zhuǎn)化為以下迭代形式:

為了確定迭代方法(8)的收斂性質(zhì)，通過引入一個恒等式關(guān)系(Golub 和Varga[14])，將(8)轉(zhuǎn)化為下列形式:

下面，假設(shè)x*是SOCAVE(1)的唯一解，其滿足下列形式:

因此，在(10)的第一個等式減去(11)的第一個等式，同時在(10)的第二個等式減去(10)的第二個等式，可以得到

取(12)中第一個方程兩側(cè)的范數(shù):

同樣取(12)中第二個方程兩側(cè)的范數(shù):

于是

用字母G 定義不等式右側(cè)的矩陣

由此可知，若ρ（G）<1，則由迭代方程組(10)生成的迭代序列將收斂到(1)的唯一解x*。

定理1如果系數(shù)矩陣A∈Rn×n在SOCAVE(1)中滿足‖A-1‖<1，其中包含的參數(shù)θ 滿足以下不等式:

那么對于任意兩個初始向量x(0)和x(1),ITSM 算法(10)生成的迭代序列收斂到(1)的唯一解x*。

3 數(shù)值實驗

為說明二階錐絕對值方程組慣性two-sweep 迭代法的有效性，給出了兩個數(shù)值模擬例子將其與另外兩種迭代算法即GN 方法[5]和MSOR-like 方法[7]進行對比。其中n 表示矩陣階數(shù),“CPU”表示平均運行時間,“IT” 表示迭代步驟的數(shù)量,“ERR” 表示誤差且ERR:=‖x(k)-x*‖(x*是精確解)，用“RES”表示絕對殘差向量的范數(shù)，短條形符號“—”表示相應(yīng)的最佳參數(shù)不存在。在我們的數(shù)值實驗中，選取零向量為迭代初始向量，選擇作為迭代的終止條件，最大迭代次數(shù)不超過1000。

此外，MSOR-like 方法中的ω 和a 滿足:

例1[7]假設(shè)SOCAVE(1)中的系數(shù)矩陣A 和常數(shù)項b 是如下形式:

其中：x*=（-1,1,-1，1，…,-1,1）∈Rn。

在這個實驗中，考慮單個二階錐的情形即r=1，其中在MSOR-like 和ITSM 方法中滿足‖A-1‖<1 這樣的假設(shè)。首先，我們比較了文獻[5]中的GN 方法、文獻[7]中的MSOR-like 方法和ITSM 方法的數(shù)值性能，表1 列出了相應(yīng)的數(shù)值結(jié)果。從表1 可以看出，所有提到的方法都可以近似求解SOCAVE。從表1 中，我們發(fā)現(xiàn)MSOR-like 方法和ITSM 方法的CPU 所占用的時間要遠小于GN 方法。雖然GN 方法需要更多的CPU時間，但GN 方法得到的解更加精確。此外，我們發(fā)現(xiàn)ITSM 迭代方法不僅在迭代步數(shù)上低于MSOR-like 方法，而且在CPU 所占用的時間上要少于GN 方法和MSOR-like 方法。

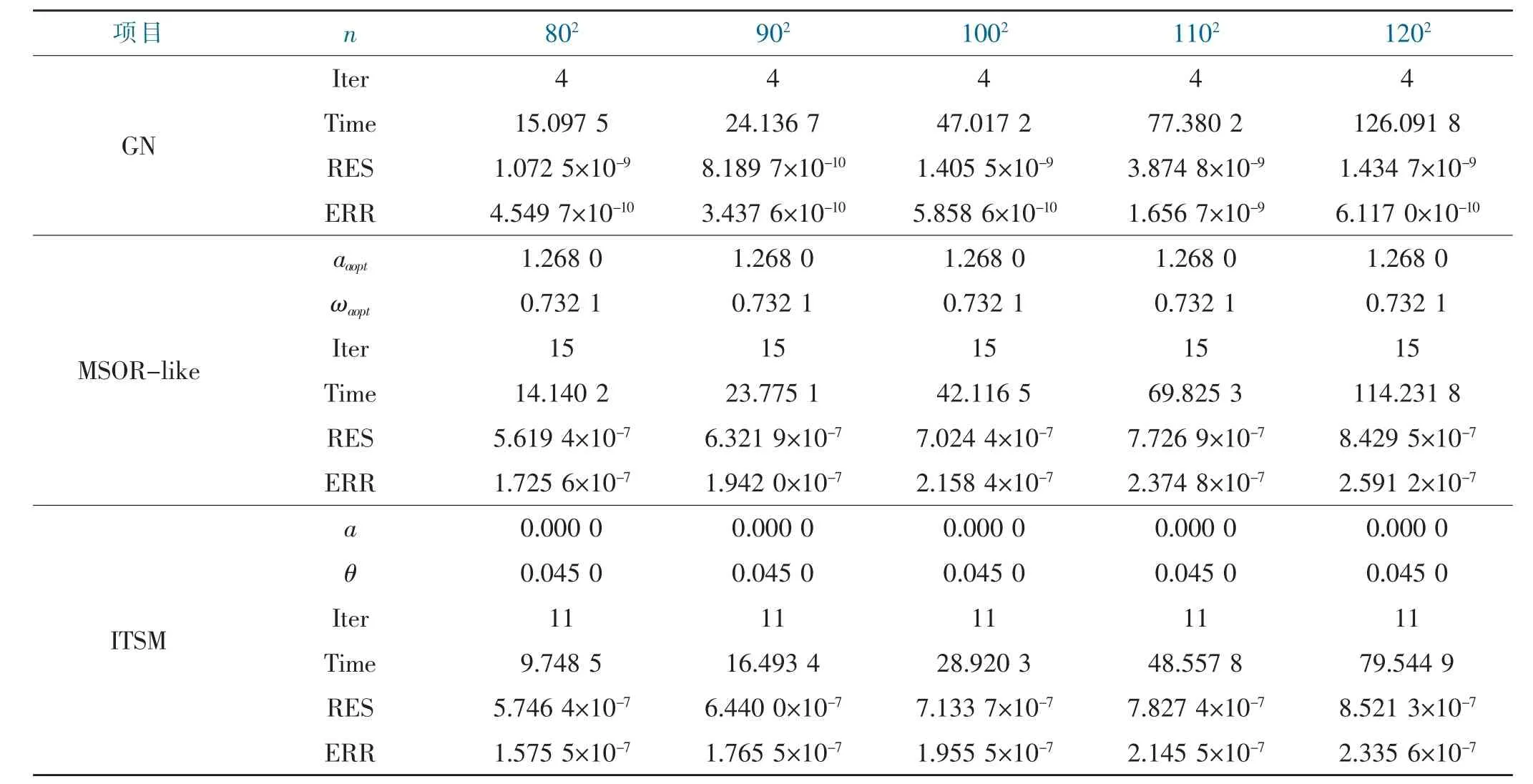
表1 GN、MSOR-like、ITSM 的比較Tab.1 Comparison between GN、MSOR-like and ITSM

例2[7]假設(shè)SOCAVE(1)中的系數(shù)矩陣常數(shù)項且b∈Rn，m 為規(guī)定的正整數(shù)且n=m2，其中:

在這個例子中，我們選擇K=Kn作為二階錐。GN方法、MSOR-like 方法和ITSM 方法這三種方法對于不同維數(shù)n 都可以有效且精確地求解。從表2 可知，GN 方法的精度都遠高于其他兩種方法。MSOR-like方法的精度幾乎與ITSM 方法相同，但ITSM 在迭代步數(shù)和CPU 時間上都要優(yōu)于MSOR-like 方法。表2 還表示，隨著n=m2的增加，MSOR-like 方法的迭代次數(shù)和CPU 時間也在增加。

表2 GN、MSOR-like、ITSM 精度比較Tab.2 Comparison of accuracy between GN、MSOR-like and ITSM

4 結(jié)論

在二階錐的框架之下引入一個慣性項和一個恒等式，提出了一種求解SOCAVE(1)的慣性two-sweep迭代方法，研究了該方法的收斂性，在適當條件下給出了保證該方法收斂的充分條件。數(shù)值結(jié)果表明該方法在迭代步數(shù)和CPU 時間方面均優(yōu)于現(xiàn)有的方法。