某型柴油機潤滑油原子發射光譜分析經驗閾值研究

吳善躍，陳 昕，任鳳華，呂 躋

（92957部隊，浙江 舟山 316000）

潤滑油原子發射光譜分析在船舶動力機械狀態監測領域得到了日益廣泛應用[1-2]。然而，在實際應用中面臨著缺乏明確判別閾值問題，極大制約了油液監測工作深入開展。針對該問題，有必要根據科學理論，利用積累的歷史數據統計經驗閾值，來指導監測工作開展。對于動力機械原子發射光譜分析監測閾值制定，現已形成多種分析方法，其中三線值法應用最為廣泛［1-5］。這些方法的使用有一基本前提，即要求樣本應符合正態分布。對于原子發射光譜分析非正態分布樣本數據應如何統計經驗閾值，文獻[5-6]對傳統方法做出了改進，但要求樣本數據符合t分布。文獻[7]所述最大熵值法實質上是一種基于分位數的閾值確定方法，雖對樣本分布沒有要求，分析簡單，但忽略了樣本分布規律，所確定閾值較粗糙。

筆者編制某型船用發電柴油機原子發射光譜分析經驗閾值時，在大樣本分析中發現多數元素樣本并不符合正態分布要求，前文所述方法均存在一定局限性。為此，本文擬以該型機為研究對象，分析樣本分布規律，探討不同分布規律樣本數據處理及閾值統計方法。

1 原始樣本分析

某型船配置有4 臺同型發電柴油機，為編制該型船發電柴油機油液光譜分析經驗閾值，收集13艘船52 臺發電柴油機油液光譜數據，共計1 741條。對上述原始樣本，采用頻數直方圖形式分析質量分數分布。繪制頻數直方圖時，先獲取樣本中最大質量分數并取整（記為Xmax），并以該整數作為樣本分組數，其分組集合為：

按以上分組繪制主要磨損元素和污染元素質量分數分布頻數直方圖，圖1～圖5為各元素質量分數分布頻數直方圖，分析直方圖可發現：①鎂元素近似正態分布，而其它元素均為非正態分布；②鐵元素近似為對數正態分布；③鋁、鉻、銅、鉛、鎳元素分布近似鐘形曲線一半；④鈉元素為不拘分布，呈明顯雙峰形態；⑤鎳、錫、銀、硼元素為不拘分布，高度集中于零值附近。上述元素質量分數分布具有明顯右拖尾現象，不僅出現零散分布，而且數值極大，尤其是鈉、鎂元素。

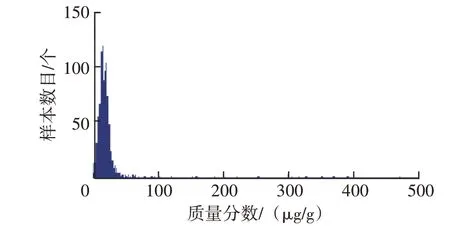
圖1 鎂元素質量分數分布頻數直方圖

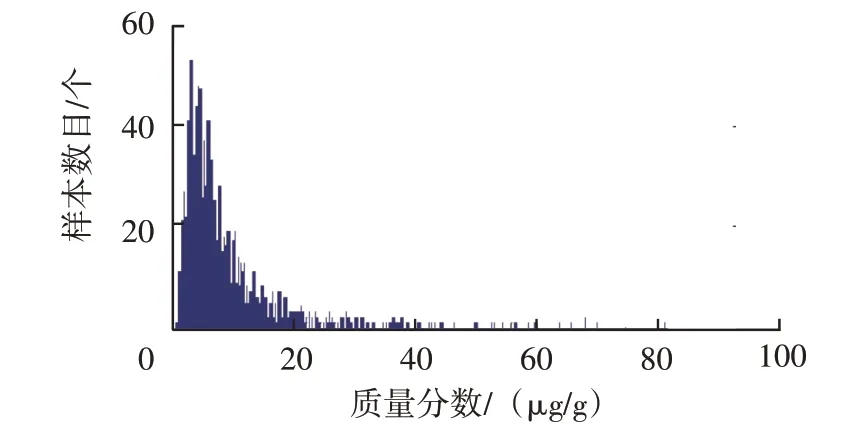
圖2 鐵元素質量分數分布頻數直方圖

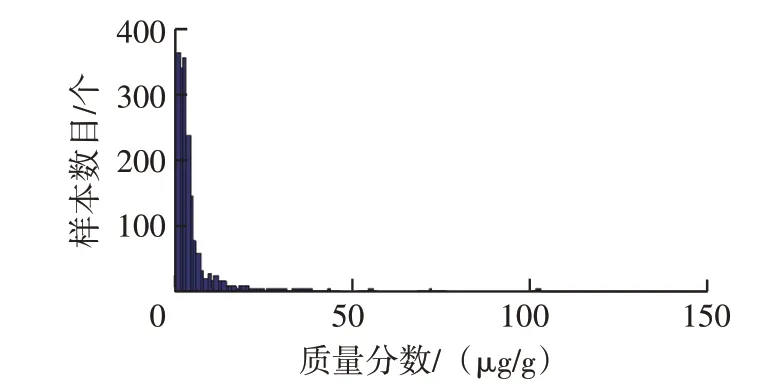
圖3 鋁元素質量分數分布頻數直方圖

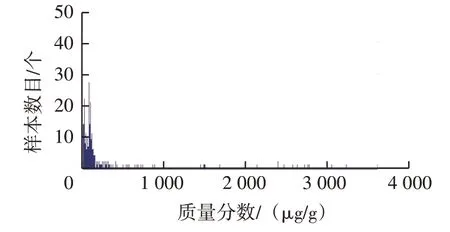
圖4 鈉元素質量分數分布頻數直方圖

圖5 鎳元素質量分數分布頻數直方圖

2 數據處理與閾值統計

圖1～圖5 代表了5 種不同分布規律原始樣本頻數直方圖，以下分別論述數據處理與閾值統計。

2.1 鎂元素

鎂元素分布基本呈正態分布，符合三線值方法使用前提。原始樣本均值（Xˉ）與均方差（S）分別為21 μg/g 和27 μg/g，以此分別作為正態分布參數μ和σ，繪制正態分布密度函數曲線，用于擬合圖1對應頻率直方圖，鎂元素原始樣本概率密度擬合曲線見圖6。由圖6 可知，該正態分布密度函數曲線并不能理想地擬合頻率直方圖，兩者之間存在較大差異。而以此正態曲線為基礎確定的三線值法預警閾值（μ+2σ）、報警閾值（μ+3σ）分別為75.0 μg/g和102.0 μg/g，數值明顯過大。

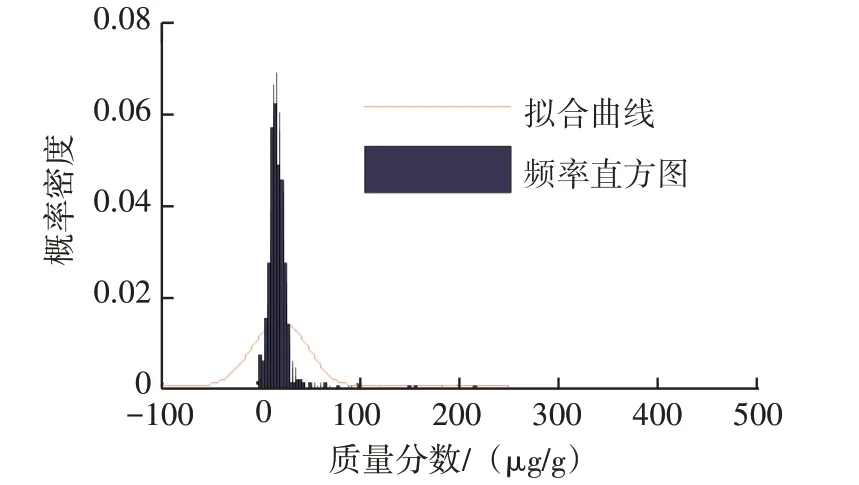
圖6 鎂元素原始樣本概率密度擬合曲線

造成以上問題的基本原因在于樣本中具有少數零散極大值數據（最大高達463 μg/g），它們對樣本均方差統計具有較大不利影響，應按一定的法則進行合理篩除。基于Xˉ+ 3S的數據篩除循環流程見圖7，本文采用圖7 篩除極大值數據，其目的是使篩除后的樣本均聚集于均值的3倍均方差范圍內，更符合正態分布。

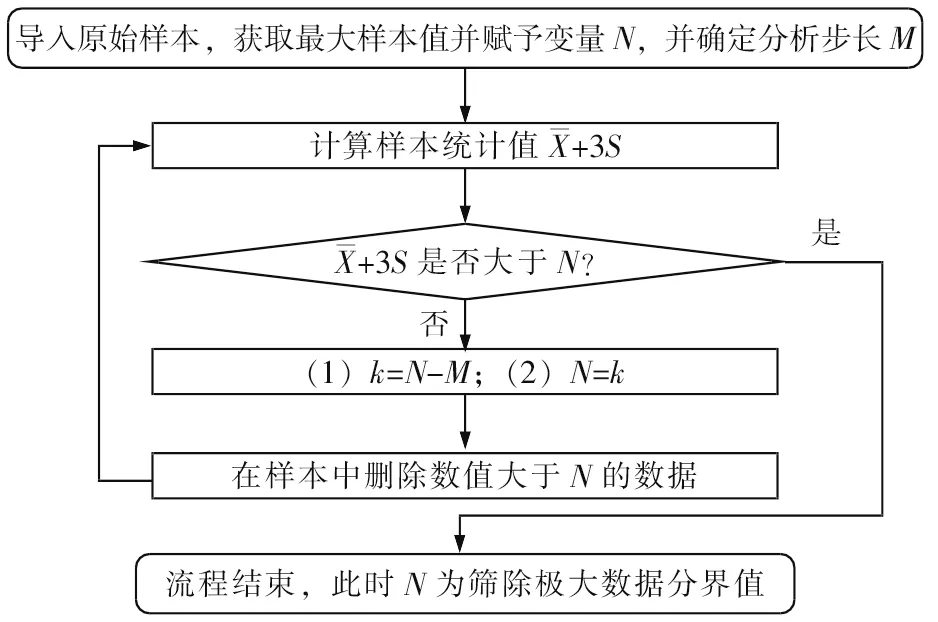
圖7 基于X+3S的數據篩除循環流程

根據圖7 篩除原始樣本中極大值數據。其中，變量賦初值情況如下：NMg為463.0 μg/g，MMg為1.0 μg/g 。流程結束時確定的篩除界限值為37.0 μg/g。篩除掉的極大值數據有64 個，約占總數的3.68%。篩除極大值數據后，計算Xˉ、S分別為17.8 μg/g 和6.4 μg/g，以此分別作為正態分布參數μ和σ，繪制正態分布密度函數曲線，就可得到篩除數據后鎂元素概率密度擬合曲線見圖8。

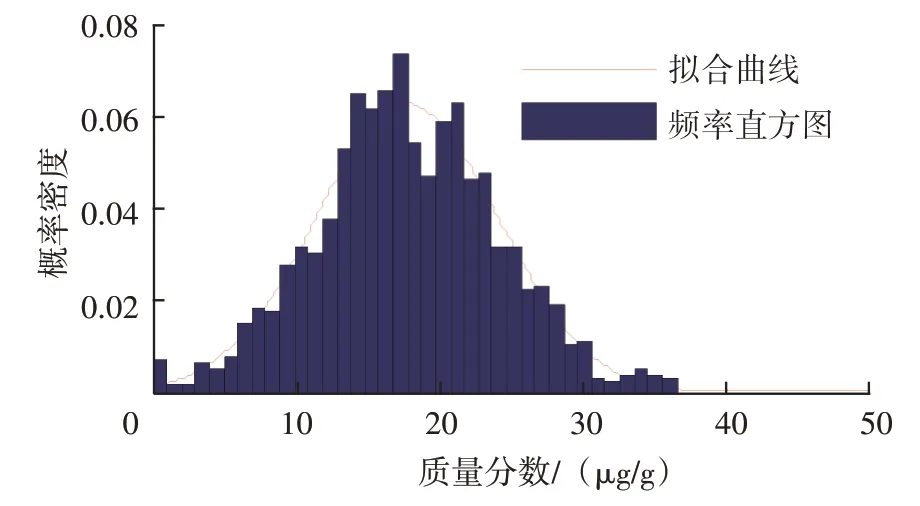
圖8 篩除數據后鎂元素概率密度擬合曲線

由圖8 可知，正態分布密度函數曲線較好擬合了頻率直方圖。根據圖8確定的正態分布概率密度曲線，可確定鎂元素質量分數預警閾值（μ+2σ）、報警閾值（μ+3σ）分別為30.6 μg/g 和37.0 μg/g，遠小于圖6的相關閾值。

2.2 鐵元素

設鐵元素質量分數原始樣本集合為{ }Xi，對該集合元素進行對數處理后變為集合{ }Yi，其中：

式中，X0為無量綱化處理的基準值，取1 μg/g。

集合{Yi}中最大值為1.96，從0～2.0 以0.05 為間隔將集合{Yi}分為40 組，并以頻數直方圖形式顯示集合{Yi}，鐵元素原始樣本對數處理后的頻數直方圖見圖9。

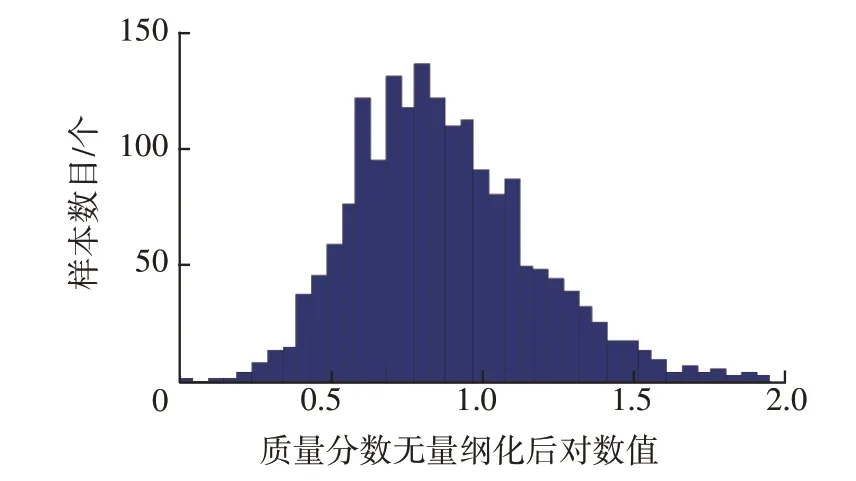
圖9 鐵元素原始樣本對數處理后的頻數直方圖

可采用正態分布密度函數曲線擬合圖9 對應的頻率直方圖。考慮到圖9 中略微存在右拖尾現象，采用圖7 中流程篩除圖9 中極大值數據。其中，變量賦初值情況如下：NFe為1.90，MFe為0.01。流程結束時確定的界限值為1.70。篩除掉的極大值數據有16個，占總數的0.92%。

篩除極大值數據后，計算Xˉ、S的值分別為0.87 和0.28，以此分別作為正態分布參數μ和σ，繪制正態分布密度函數曲線，將該曲線作為頻率直方圖的擬合曲線，對數處理和篩除數據后鐵元素概率密度擬合曲線見圖10。

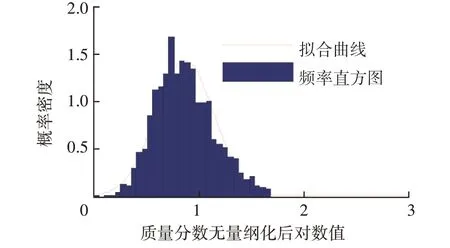
圖10 對數處理和篩除數據后鐵元素概率密度擬合曲線

由圖10 可知，正態分布密度函數曲線較好擬合了頻率直方圖，故可以由正態分布參數μ和σ確定閾值。所計算的預警閾值（μ+2σ）、報警閾值（μ+3σ）分別為1.42 和1.70，對應于對數變化前的原始值分別為26.3 μg/g、50.1 μg/g，由此最終確定這2個原始值分別為鐵元素質量分數的預警閾值和報警閾值。

2.3 鋁元素

鋁元素分布近似鐘形曲線一半（鐘形曲線左右對稱點數值為零），可考慮在正態分布密度函數曲線基礎上構建擬合分布密度函數g(x)。g(x)定義為分段函數：

式中，f(x)是均值為0的正態分布密度函數，即：

設g(x)對應的分布函數為G(x)，即：

當x→∞時，G(x) = 1。g(x)可視為f(x)負半軸部分按零軸對稱疊加到正半軸部分。由以上各式關 系 不 難 計 算G(2σ)、G(3σ) 分 別 為0.954 4 和0.997 4，可將2σ、3σ分別作為報預警閾值和報警閾值。

半鐘形分布數據篩除循環流程如圖11 所示。由于圖3樣本中存在零散極大值數據，按圖11流程篩除極大值數據。其中，變量賦初值情況如下：NAl為104.0 μg/g，MAl為1.0 μg/g。

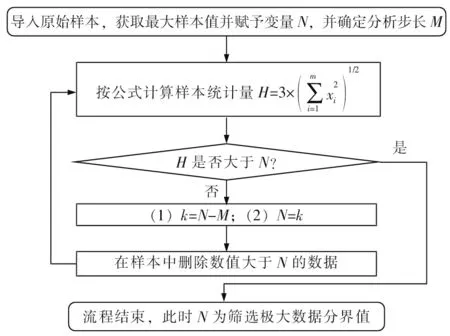
圖11 半鐘形分布數據篩除循環流程

流程結束時篩除極大值數據的界限值為11.0 μg/g。篩除掉極大值數據112 個，約占總數的6.43%。針對篩除極大值數據后樣本，計算2 階原點矩平方根為3.5 μg/g，將其作為參數σ，繪制f(x)、g(x)函數曲線，鋁元素概率密度擬合曲線如圖12 所示。由圖12 可知，g(x)能較好擬合頻率直方圖，2σ、3σ的計算值為7.0 μg/g和10.5 μg/g，把該值作為預警閾值和報警閾值。

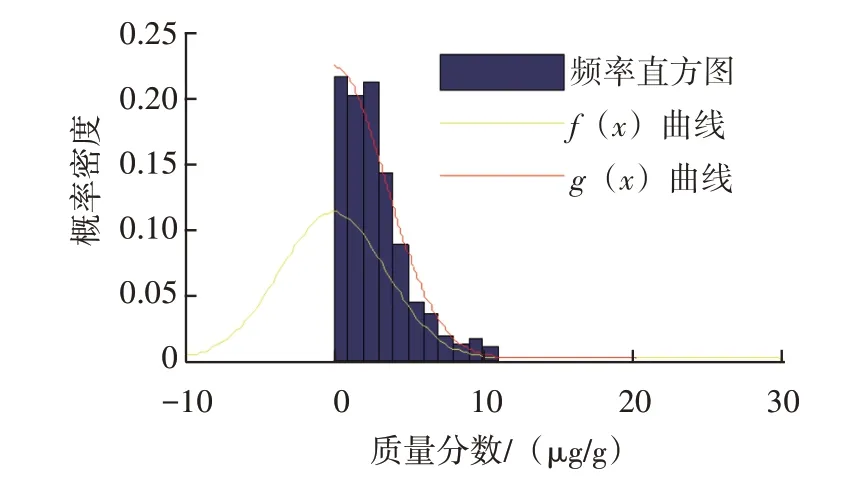
圖12 鋁元素概率密度擬合曲線

2.4 鈉元素

圖4 中鈉元素分布具有數值極大的零散數據（最大為3 479.0 μg/g），先采用圖7 流程進行極大值數據篩除。其中，變量賦初值情況如下：NNa為3 479.0 μg/g，MNa為1.0 μg/g 。流程結束時篩除極大值數據的界限值為182.0 μg/g。篩除掉的極大值數據有102 個，約占原始樣本的5.8%。篩除數據后鈉元素頻數直方圖如圖13 所示，樣本分布不僅與正態分布相差甚遠，而且具有2 個明顯聚集區域（分別為0～40.0 μg/g 和70.0～120.0 μg/g）。該樣本屬于不拘分布，無法使用常見分布密度曲線擬合頻率分布直方圖。只能直接采用分位數法確定閾值。

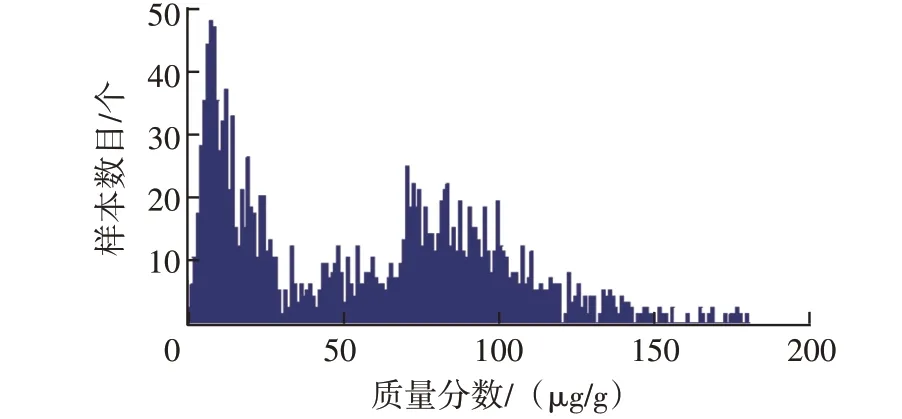
圖13 篩除數據后鈉元素頻數直方圖

考 慮 到 在 正 態 分 布 中 區 間[-∞，μ+ 2σ]、[-∞，μ+ 3σ]對應的概率為97.72%和99.87%，可將圖13樣本中97.72%、99.87%分位數設為預警閾值和報警閾值，分別對應為139.7 μg/g、182.0 μg/g。

2.5 鎳元素

考慮到圖5 樣本高度集中于零值附近，參考圖12 流程進行極大值數據篩選。變量賦初值情況如下：NNi為29.0 μg/g，MNi為0.1 μg/g。流程結束時，確定的極大值數據界限值為1.0 μg/g。篩除掉的極大值數據160 個，占總數的9.19%。篩除極大值數值后，在0～1.0 μg/g區間內以0.1 μg/g為間隔顯示樣本頻數直方圖，篩除數據后鎳元素頻數直方圖見圖14。

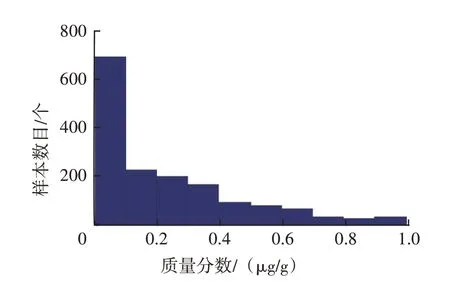
圖14 篩除數據后鎳元素頻數直方圖

該樣本屬于不拘分布，無法使用常見分布密度曲線擬合頻率分布直方圖。只能直接采用分位數法確定閾值。將97.72%、99.87%分位數設為預警閾值和報警閾值，對應數值分別為0.8 μg/g、1.0 μg/g。

3 討論分析

各元素閾值見表1。一些從事柴油機油液監測的技術人員在統計經驗閾值時，不注重考慮樣本分布是否符合正態分布及零散極大值處理，直接通過Xˉ、S確定閾值T1和T2。這一處理方式過于簡單，所確定數值與前文所述閾值（見表1 中預警值、報警值）存在較大差異。其中，鎂、鋁、鈉、鎳元素的T1 和T2 值，遠大于前文確定的預警值和報警值；鐵元素T2 值則偏低，明顯小于報警值。表1中，T1為Xˉ+ 2S，T2為Xˉ+ 3S。

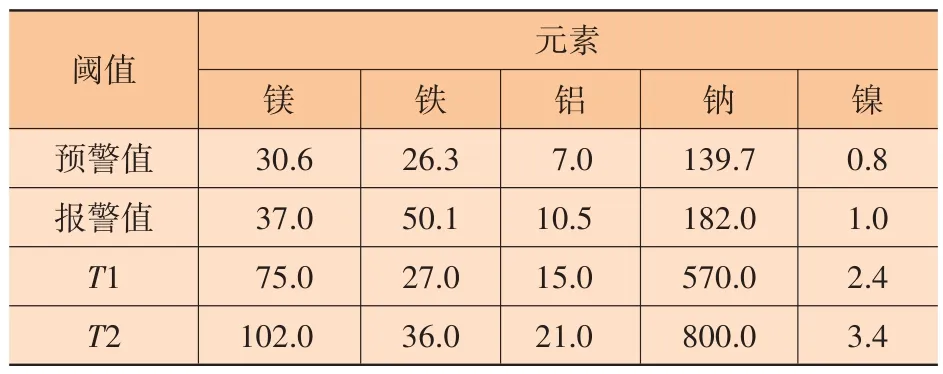
表1 各元素閾值 μg/g

閾值是否合理需通過實踐進行分析。一是以故障案例數據為基礎的參考分析。例如，我單位監測工作中曾發現潤滑油受海水污染案例，其鈉、鎂元素質量分數分別為240.0 μg/g 和38.1 μg/g，如果用表1 中T1、T2 值作隱患判別，會出現漏報情況。二是關于裝備使用及維護保養情況調研分析。例如，對鐵元素質量分數位于36.0～50.1 μg/g 之間樣本進行調研分析，了解相關船舶取樣前后一段時間內裝備維護保養情況，并未發現缸套、氣閥、傳遞齒輪等鐵元素主要來源部位存在異常問題，說明以鐵元素T2 值（36.0 μg/g）作為報警值過于保守。綜合以上分析不難看出，直接通過Xˉ與S確定閾值是不合理的。相比較而言，前文所述方法確定的預警值和報警值更符合實際。

理想的閾值應能對故障隱患及時做出報警，避免故障漏報，并盡可能減少虛報問題發生。前文確定的預警值和報警值還只能稱為經驗閾值，要達到理想閾值標準還有待在后續監測實踐中不斷檢驗和修正。

4 結束語

1）該型柴油機光譜分析數據中絕大多數元素原始樣本并不符合正態分布，并伴有明顯拖尾現象，直接采用傳統的三線值方法統計經驗閾值是不合理的。

2）應根據樣本分布特點選擇恰當數據處理方法統計經驗閾值。本文對5種典型分布采用了不同數據處理方法，可作為類似問題分析參考。

3）零散極大值數據會使統計的經驗閾值過大，分析時有必要對極大值數據做相應篩除。針對不同分布，本文采用的基于Xˉ+ 3S的篩除循環流程和半鐘形分布數據篩除循環流程，可獲得理想的數據篩選效果。

4）相比傳統方法閾值，本文方法確定經驗閾值更為合理，但還需在監測實踐中不斷檢驗與修正。