問題驅動 類比遷移 生長思維
——以“一次函數與二元一次方程”為例

王永鋒

江蘇省蘇州市吳江區盛澤第二中學 (215228)

《義務教育數學課程標準》(2022版)指出:體會數學知識之間、數學與其他學科之間、數學與生活之間的聯系,在探索真實情境所蘊含的關系中,發現問題和提出問題,運用數學和其他學科的知識與方法分析問題和解決問題．基于此,數學課堂教學要以培養學生發現、提出、分析和解決問題的能力驅動設計,體現知識的類比遷移,培養學生的生長思維．素養導向的初中數學課堂教學中,問題才應該是數學學習的生命線,以情境產生問題,以問題驅動思考,引發學生持續、深入的探究,感受數學知識生長的全過程．本文以蘇教版《義務教育課程標準實驗教科書·數學》八年級上冊“6.5一次函數與二元一次方程”為例,談談基于問題驅動,喚醒知識經驗,巧妙類比遷移,自然生長思維的教學過程．

一、于情境創設中跨學科引入,讓學生體會數學之美

教學的藝術不在于傳授,而在于激勵、喚醒和鼓舞學生的心靈．數學教學時,教師要創設真實的學習情境,這不僅可以吸引學生的注意力,而且有利于學生發現問題,探索新知．北京大學郭華教授指出:數學學科主動走出去,將其他相關學科積極請進來．在這個過程中以“我”為主、以“我”為本,同時將其他學科的知識和方法為“我”所用、助“我”成事．[1]跨學科引入的問題情境,必然是課堂教學的潤滑油與催化劑．這里講的跨學科引入,是指為學生提供恰當的學習情境,將本學科之外的學科知識置于學習情境中,從知識或方法的交叉處提煉出具有數學學科意義的關鍵概念,并對其進行思考和探索的教學過程．本課引入將語文學科的古詩詞在數學課堂中呈現,以古詩詞對仗之美烘托數學符號之美,以古詩詞的意蘊之美關聯數學本質之美,以古詩詞細膩的情感之美映射數學嚴謹的科學之美,學生美不勝收．

片斷1：課堂引入問題設計

(1)我們學過北宋詩人蘇軾的《題西林壁》,一起大聲朗讀,并請語文課代表談一下感受?

(2) 對于關系式y=-x+5,你能從不同的角度談一談對它的認識嗎?請數學課代表談一下感受?

設計意圖：唐詩宋詞是我國的文化瑰寶,傳承至此,歷久彌香．一首《題西林壁》告知我們要從不同的視角觀察問題,才能得到問題的本質．對關系式y=-x+5,從不同的視角來觀察,既是二元一次方程,也是一次函數,本質上都是表示兩個變量之間的關系,兩位課代表很好地解釋了各自表達的主旨．將語文古詩詞融入數學教學,學生于問題驅動中類比遷移,于跨學科引入之美中自然得出“一次函數和二元一次方程”這一研究主題．跨學科引入研究主題,關鍵是依托教師的引,促進學生的悟．跨學科引入實際上就是利用學科知識進行現實生活的觀察和問題解決,它以課程標準為依據,以學生的經驗為基礎,圍繞學科本質而開展．基于此,跨學科一定要讓學生自己動起來,在發展人文的基礎上增加濃厚的趣味性,選取“為我所用”的知識、材料和技能,去作出調整,既能促進學科之間的本質融合,又能感受數學的內在美．

二、于操作探究中找本質,讓學生悟出知識關聯

現代認知結構理論認為,學習不是教師向學生傳遞知識,而是學生自己建構知識和應用知識的過程．它以學生為中心,強調學生的親身體驗,強調學生對知識的嘗試發現和對所學知識意義的主動建構．數學是一門“做”的學科,學生通過動手操作和探究交流,激活已有的經驗和知識儲備,找準思維的最近發展區,厘清知識之間的內在關聯,撥開形式不同的“面紗”找準其中蘊含的本質．鄭毓信教授說:“基礎知識不在于求全,而在求聯．”“求聯”的著力點在于以問題驅動思考,讓學生親身經歷,參與實踐,以舊知喚醒新知,悟出知識關聯,形成個性化的理解．教學時,教師設計的問題以問題串形式出現,讓學生學會有條理的思考,培養學生的思維能力．

片斷2：課堂探究問題設計

(1)一次函數y=-x+5與二元一次方程x+y-5=0之間有怎樣的聯系?

(2)二元一次方程x+y-5=0的解與一次函數y=-x+5的圖像上的點有什么關系?

(3)畫出一次函數y=-x+5的圖像,在圖像上任取3個點,并寫出它們的坐標．你發現了什么?

(4)再寫出方程x+y-5=0的3個解,以這3個解為坐標,在上述直角坐標系中描出這3個點．你又發現了什么?

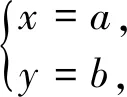
(6)把上述一次函數的關系式一般化,可得y=kx+b(k,b是常數且k≠0),相應的二元一次方程為kx-y+b=0．它們之間還滿足上述的關系嗎?

設計意圖：美國數學家布魯納指出:“數學過程是一種提出問題和解決問題的持續不斷的活動,思維永遠是從問題開始的．”問題(1)中的一次函數y=-x+5與二元一次方程x+y-5=0,可以通過移項相互轉化,它們都是表示x、y相同的數量關系．問題(2)地解決要依托解決問題(3)和問題(4)來領悟,于學生而言,這也是學習本節課的學習難點．教師需引導學生選取“兩個關鍵點”畫出一次函數的圖像,并在圖像上取出不同的點,進一步感受這樣的點有無數個,并且它們都是相應的二元一次方程的解．接下來,對二元一次方程的解進行描點,發現這些點都在一次函數的圖像上．由于這個操作只能選取有限個點,教師可結合幾何畫板加以演示,讓學生深刻領悟兩者蘊含其中的關聯．問題(5)是對問題(3)、(4)的特殊點的一般化歸納,也是對解和坐標關系的一般性詮釋．從問題(1)知曉關系式可以相互轉化,自然也就不需要將問題(5)中的坐標代入驗證了．由此可以引導學生悟出:一次函數y=-x+5圖像上點的坐標是二元一次方程x+y-5=0的解;同時,二元一次方程x+y-5=0的解是一次函數y=-x+5圖像上點的坐標．問題(6)是問題(2)的一般化歸納,它是上述5個問題的總結,在本節課起著承上啟下的作用．問題是數學的心臟,通過問題串優化問題設計,激活學生的知識積淀,優化學生的數學技能,豐富學生的情感體驗,化抽象為具體,深入淺出讓學生悟出“點的坐標”和“方程的解”的關聯．

三、于類比遷移中現靈魂,讓學生領會思想方法

《義務教育數學課程標準》(2022版)指出:通過豐富的教學方式,讓學生在實踐、探究、體驗、反思、合作、交流等學習過程中感悟基本思想、積累基本活動經驗,發揮每一種教學方式的育人價值,促進學生核心素養發展．數學思想方法是從數學內容中提煉出來的數學學科的精髓,是將數學知識轉化為數學能力的橋梁和紐帶,是數學知識本質和內在聯系的反映,是數學創造和發展的源泉,是數學學習的靈魂所在,具有高度的抽象性和概括性．數學思想方法不是解題的模型和套路,而是數學文化的本質和內核．它是動態的,發展的,是數學應用的關鍵,要從關注學生的長遠發展進行針對性的化隱為顯,逐步滲透．學生只有領會了思想方法,才能靈活運用知識,真正發展數學能力．

片斷3：課堂提升問題設計

(1)練習:已知點M(0,3)和N(1,4)在一次函數y=kx+b的圖像上,求一次函數的表達式．你這樣做的依據是什么?

(2)在同一個坐標系中畫出一次函數y=x+3的圖像,它和函數y=-x+5有怎樣的位置關系?同一平面內的兩條直線還有怎樣的位置關系?

設計意圖：數學思想是對概念、方法和理論的本質認識;數學方法是處理數學問題中所采用的各種手段、途徑和方式．設計問題(1)目的有二:一是復習求一次函數關系式的求解方法,二是解釋這樣做的依據,即“坐標是解”．問題(2)結合前面所畫的一次函數y=-x+5的圖像,直接得出這兩條直線相交(垂直),同一平面內的兩條直線的位置還可能平行,這就為解決問題(4)埋下伏筆．問題(3)是研究兩條直線的交點和對應的二元一次方程組的解之間的關系,通過類比遷移,學生自然會得出兩者之間的關系．結合教學片段2和3,學生很好地感受到點(解)的特殊到一般,函數關系式(二元一次方程)的特殊到一般,感受“形”(一次函數的圖像)與“數”(二元一次方程)的巧妙結合,感受一條直線(一個方程)到兩條直線(兩個方程)的類比與轉化．教師不斷地設問、發問、提問、追問,學生不斷地長思考、深思考、全思考、慢思考,在師生共同體驗中,積極參與數學問題生成與分析解決的全過程,透過知識這個載體,感受數學思想方法的滲透與突出,逐漸提升數學素養．

四、于歸納總結中會思考,讓學生自然生長思維

數學家康托爾說:“數學的本質在于它的自由．”這里的自由即是一種理性思維自由的創造．因此,在數學課堂上,教師不能依賴于大容量、快節奏的教學方式對學生狂轟濫炸,而是要留給學生充足的思考時間,讓學生自由地思考和表達,讓不同的人得到不同的體驗和發展．“編筐編簍,重在收口．”數學課的最后階段,留下幾分鐘讓學生暢談感受甚至是寫寫感悟,對一節課的學習過程進行歸納總結,讓學生親身體驗數學“再發現”和“再創造”的過程,獲得進一步發展所必需的數學活動經驗來發現和提出問題,用數學思維來分析問題,用數學語言來表達并解決問題,這對完善學生的認知結構,發展學生的思維大有裨益．

片斷4:課堂總結設計問題

(1)用圖像法解二元一次方程組的步驟是什么?與消元法相比,它的優缺點是什么?

(2)這節課是怎樣學習函數與方程間關系的?請畫出它的知識結構圖．

(3)在探索過程中滲透了哪些數學思想和方法?

(4)再讀《題西林壁》,你又有怎樣的感受?

設計意圖：瑞士教育家裴斯泰洛奇說:“教學的主要任務不是積累知識,而是發展思維．”本環節中,問題(1)通過觀察操作,類比抽象,總結歸納出用圖像法解二元一次方程組需“變函數——畫圖像——找交點——寫結論”四個步驟．與七年級學過的消元法相比,圖像法更為直觀,確定交點坐標便可以直接寫出相應的方程組的解,但是未知交點坐標則只能求出近似解．問題(2)是對整節課教學流程的一個回顧,教師引導學生畫出如圖1所示的思維結構圖,完善學生的知識結構體系．數學在某種程度就是一種系統和結構,結構上一以貫之,知曉通性才有通法可徇．[2]問題(3)是對知識體系形成過程的高度抽象和概括,突出強調類比、數形結合、特殊到一般等思想方法．問題(4)與課堂引入首位呼應,是本節課人文性的升華．審視本環節的學習,學生獲得“四基”的過程與結果相互交融,發展“四能”的目標層層遞進,于歸納總結中深入思考,厘清知識脈絡,提升能力,生長思維,落實素養．

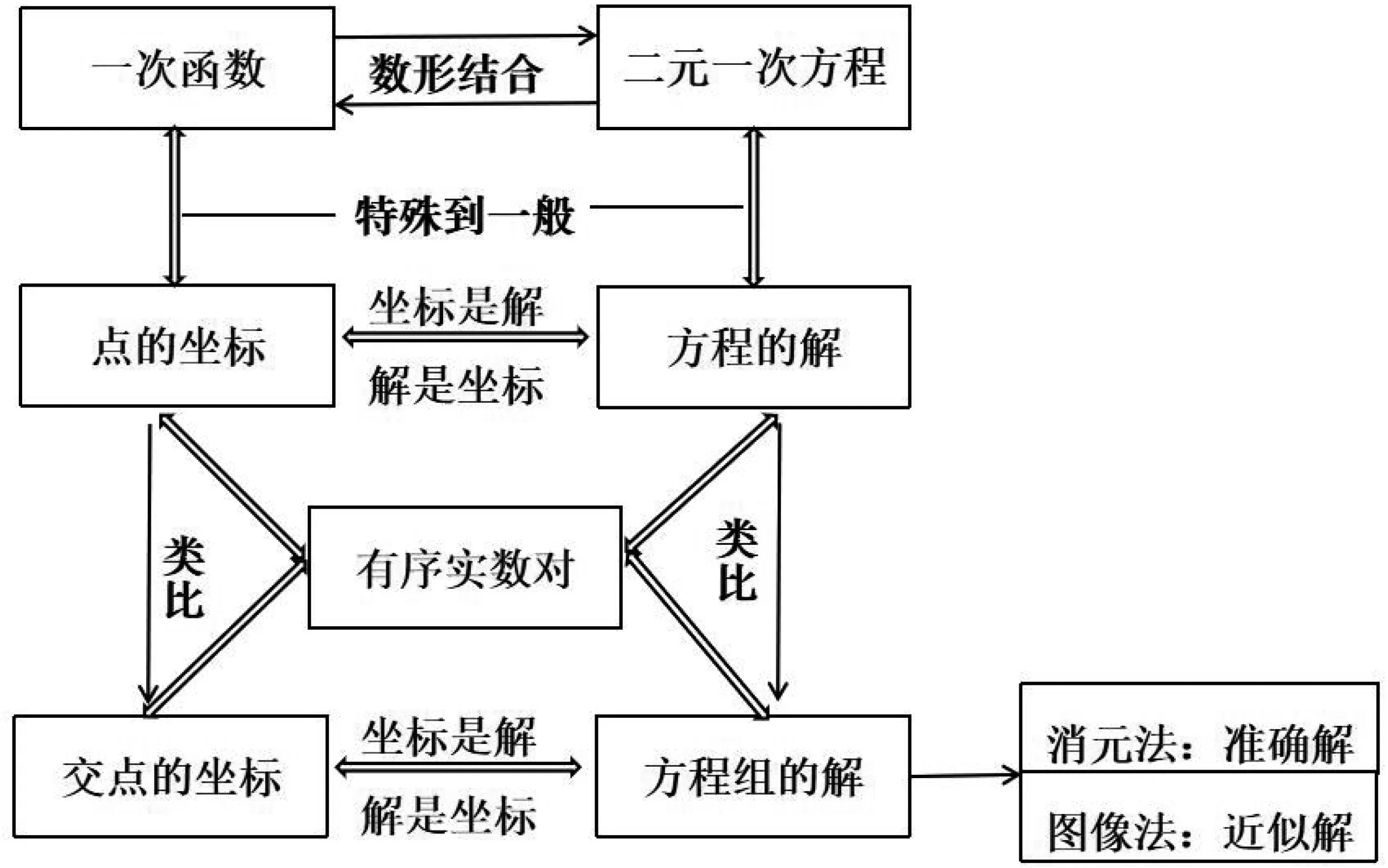
圖1

“教育的出發點和落腳點就是讓學生經歷一種成長,見證一種成長”．基于此,教師要找準生長點,以問題驅動教學,為學生創設豐富的表達個人觀點的情境,給學生知無不言、言無不盡的表述機會．只要學生敢于開口,樂于操作,勤于總結,必然優化思維品質,培養思維能力,發展數學素養．