一道2022年江西預賽試題的多解探究與變式
2023-11-10 12:10:20徐鳳旺尹正波
中學數學研究(江西) 2023年11期
成 敏 徐鳳旺 尹正波
貴州師范大學數學科學學院 (550025)
1 試題呈現
分析:這是2022年全國高中數學聯賽江西賽區的一道根式函數求最大值的試題.文[1]通過三種方法求得該函數的最大值,并對其試題進行了相應的變式,讀后深受啟發,于是對該題做進一步的探究,得到了不同于文[1]中的三種解法和試題的幾個變式,與大家一起分享.
2 試題解析
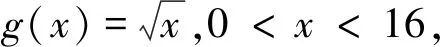
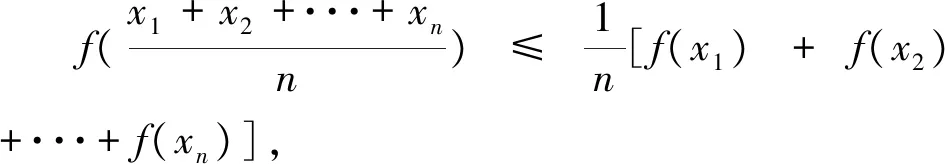
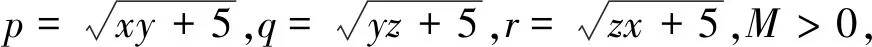
評注:此解法通過換元法,構造二次函數,將問題轉化為二次函數的Δ≤0,即可求得該函數的最大值.
解法3:(構造隨機變量X的分布列)由題意可得,可構造隨機變量X的分布列為:

Xxy+5yz+5zx+5P131313
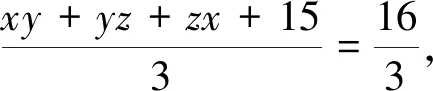
評注:此解法通過構造隨機變量X的分布列,結合(EX)2≤EX2,求得函數的最大值.
3 試題變式
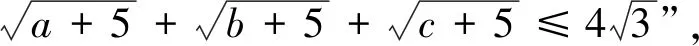
3.1 三元形式的變式
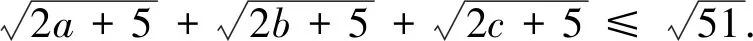

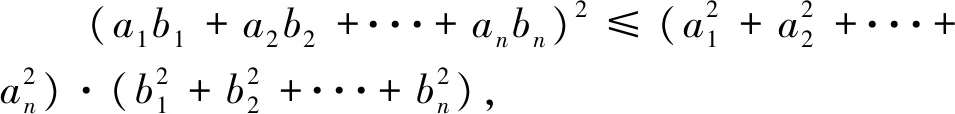
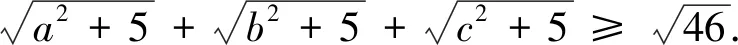
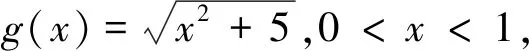
評注:此變式是將不等式每一項根號下未知數的冪從“1”變為“2”得到.
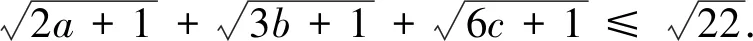

評注:此變式是將不等式每一項根號下的未知數的系數和常數項改變得到.
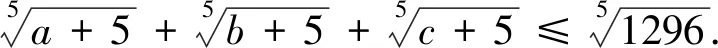
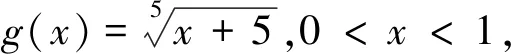
評注:此變式是通過改變不等式每一項的冪得到.
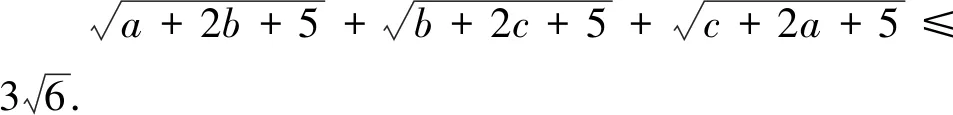
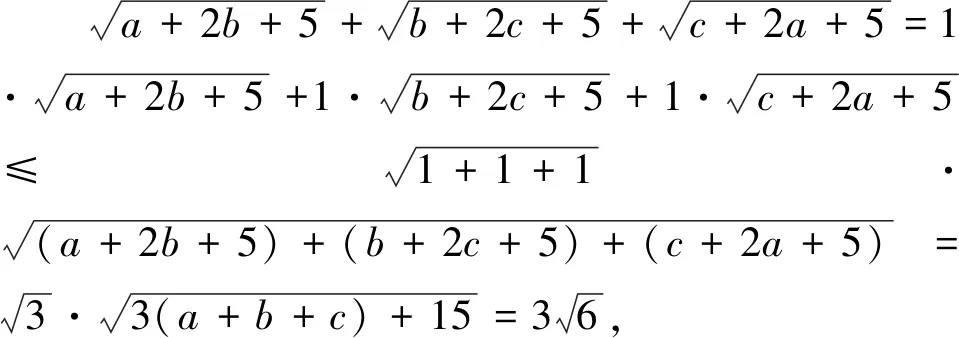
評注:此變式是通過改變不等式每一項根號下的代數式的結構得到,將每一項根號下未知數的個數從“1”元變為“2”元.
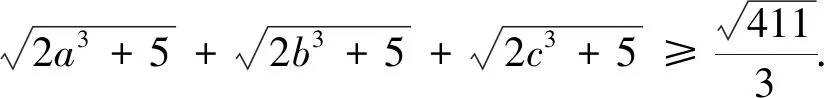
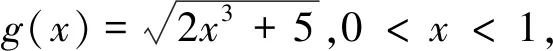
評注:此變式是通過改變不等式每一項根號下的未知數的冪和系數得到.
3.2 四元形式的變式


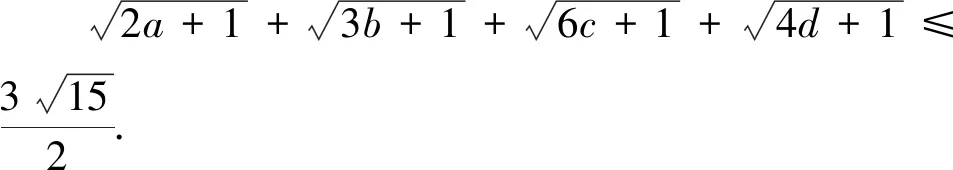
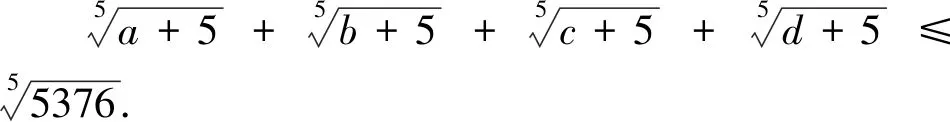
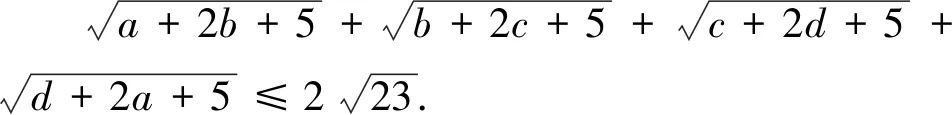

上述變式7到變式12均是在變式1到變式6的基礎上改變的,將未知數的個數從“3”元變到“4”元,變式7到變式12的證明方法分別對應變式1到變式6的證明方法,證明方法一致,此處不再敘述.
猜你喜歡
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
中等數學(2021年11期)2021-02-12 05:11:46
今日農業(2019年14期)2019-09-18 01:21:42
兒童故事畫報(2019年5期)2019-05-26 14:26:14
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

