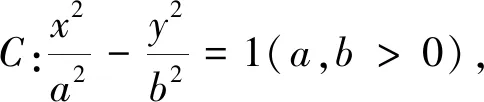橢圓曲線中斜率之積為定值的解法探究
張 侶
重慶市忠縣中學校 (404300)
圓錐曲線定點、定值問題已成為高考或模擬考試中的重點考查對象,其求解過程往往涉及豐富的知識內容和靈活運用的數學思想.試題通過具體數據的巧妙設問,獲取一些特殊結論,這些結論看似特殊,實則具有普遍性,此類試題的研究不僅能夠抓住圓錐曲線的本質,還能透過試題挖掘隱含的命題規律,更能將其拓展到一般情況.本文以一道聯考橢圓試題為例進行解法探究,幫助學生熟悉求解此類問題的常用方法,從而獲得更多解決此類問題的思考方向.
1 試題呈現
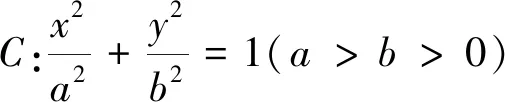
試題分析:該題主要考查橢圓的標準方程及其幾何性質、橢圓中直線斜率的幾何關系以及斜率乘積為定值問題等內容,重點考查學生的數學運算能力,推理論證能力以及綜合運用所學知識分析問題和解決問題的能力.試題結構清晰,問題設置層次分明,內容豐富,第一問較簡單,易于求解,本文嘗試對第二問從不同的角度進行求解,并探究其一般性結論.此題為階段性檢測學生的學習潛能起到了較好的引導作用.
2 解法探究
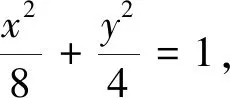

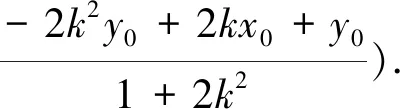
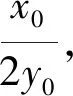
評析:通過聯立直線MP方程與橢圓方程得出點P的坐標,再根據題意,將斜率k用-k替代后得到點Q的坐標,利用兩點間的斜率公式算出k1和k2,最后解得k1·k2的值.
評析:通過聯立直線PQ方程與橢圓方程得出x1+x2與x1·x2的表達式,根據題意,結合點M在橢圓上以及kMP+kMQ=0,算出k1和k2,最后解得k1·k2的值.
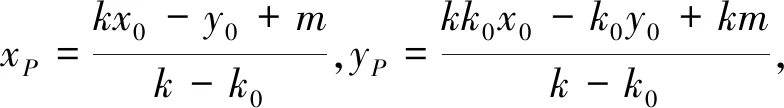
評析:通過設過點M的直線方程和直線PQ的方程,解出點P的坐標,將點P代入橢圓C方程,獲得關于kMP,kMQ為兩根的一元二次方程,結合韋達定理和題設條件,以及兩點間的斜率公式,算出k1和k2,最后解得k1·k2的值.
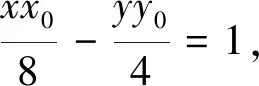
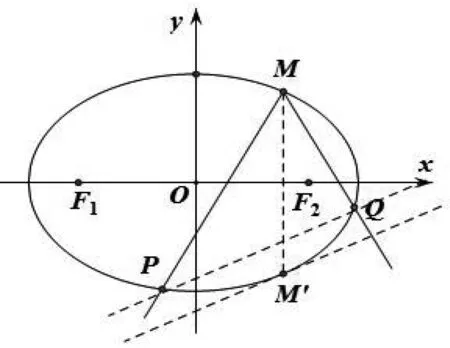
圖1
評析:利用極限思想,巧妙地將問題求斜率k1的表達式等價轉化為求過M′處切線的斜率,結合切線方程和兩點間的斜率公式,算出k1和k2,最后解得k1·k2的值.
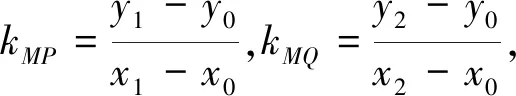
評析:通過改寫橢圓方程和巧設直線方程,獲得關于kMP,kMQ為兩根的一元二次方程,結合韋達定理和題設條件,以及兩點間的斜率公式,算出k1和k2,最后解得k1·k2的值.
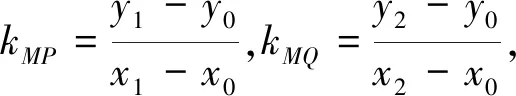
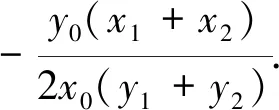
評析:根據P,Q,M三點在橢圓上,利用點差法以及題設條件kMP+kMQ=0,獲得相應等式關系,從而算出k1和k2,最后解得k1·k2的值.
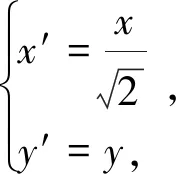
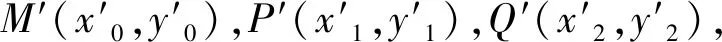
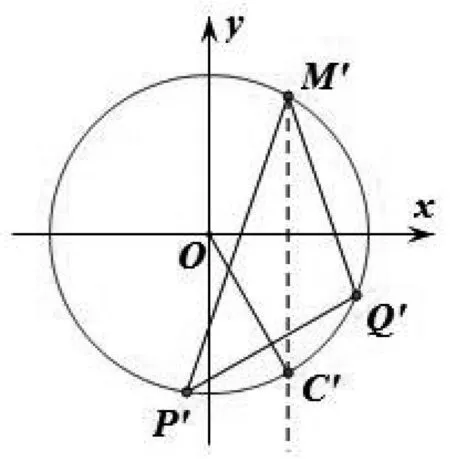
圖2
評析:此法通過伸縮變換,將橢圓方程變換為圓的方程,便將問題轉化為關于直線和圓的問題,利用圓的性質,最后解得k1·k2的值.
3 推廣探究
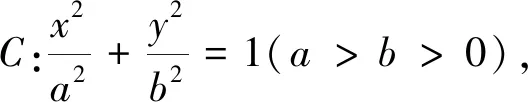
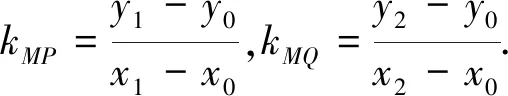
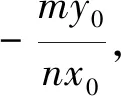
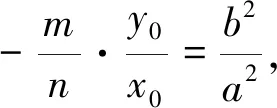
結合以上求解過程,可獲如下結論1.
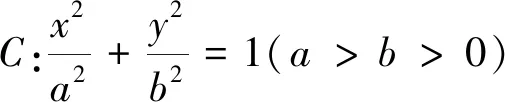
由于橢圓經過伸縮變換,可以得到以坐標原點為圓心的圓,類比可得如下結論2:
結論2 已知圓C:x2+y2=R2,若圓C上的動點M,P,Q滿足直線MP,MQ的斜率互為相反數,且點M不在坐標軸上,設直線PQ,OM的斜率分別為k1,k2,則k1k2=1.
類比可得雙曲線中的如下結論3.