例探初中生符號意識形成路徑*

劉 靜 鐘珍玖

江蘇省江陰市第一初級中學 (214432)

七年級是從小學的算術思維向用字母表示數形成代數思維的啟蒙期,八年級則是學生符號意識形成的關鍵期.從學生認知能力來看,八年級學生抽象能力迅速發展,已經基本能夠借助符號進行形式化演繹推理;從學習內容來看,軸對稱圖形(線段、角、等腰三角形)和中心對稱圖形(平行四邊形、菱形、矩形、正方形)是初中階段運用符號進行邏輯推理核心內容,也是符號意識形成的最佳素材;一次函數和反比例函數的學習豐富了符號語言的種類,用函數圖像來表達函數是符號意識形成新的突破口.在八年級的教學中有目的、有意識的加強學生的符號意識,讓學生主動理解與運用符號,從而提高數學表達的能和習慣,落實學生的核心素養.

一、 在幾何教學中運用符號推理,強化符號的思維功能,滲透符號意識

幾何演繹推理遵循著《幾何原本》的公理化思想,由已知的公理和定義,用邏輯推理的方法推導出其它數學定理和命題.教材的編寫也遵循同樣的思想,研究幾何圖形的性質都是把定義作為基本事實,然后用邏輯推理的方法得出圖形的性質及判定方法.幾何定義、公理、定理的表達和幾何推理的過程都需要較強的符號意識支撐,數學的形式化、結構化、操作化都離不開數學符號的表達[1].羅素認為:數學就是符號加邏輯.幾何圖形之間的關系包括數量關系和位置關系,應培養學生用符號刻畫這些關系的意識,符號意識的發展有利于學生理解符號的使用和進行數學思考,強化符號意識的同時,獲得知識,發展學生的邏輯推理能力.

案例1 蘇科版教材八年級上冊“2.4線段、角的抽對稱性”.

如圖1,若△ABC的角平分線AD、BE相交于點P．求證:點P在∠C的平分線上.

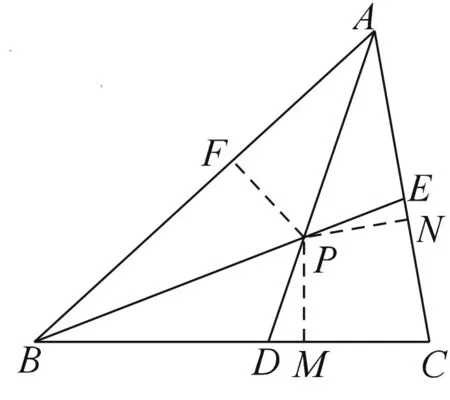
圖1

證明：過P作PM⊥CB,PN⊥CA,PF⊥AB,垂足分別為M、N、F.∵EB平分∠CBA,PM⊥CB,PF⊥AB,∴PM=PF.∵AD平分∠BAC,PN⊥CA,PF⊥AB,∴PF=PN.∴PM=PN,PM⊥CB,PN⊥CA,∴點P在∠C的平分線上.

從教學實踐來看,八年級學生對于這些圖形位置關系的問題非常陌生,不容易入手,從直觀上來說點在直線上很好理解,但是用符號語言如何表達?其中又蘊含著怎樣的圖形特征?對這些問題的追問可以幫助學生找到問題的解決方法,強化用符號推理的功能,深刻理解符號表達的思維價值.

教學策略：八年級是學生邏輯思維能力發展的關鍵學段,而符號語言是思維的載體和抓手,符號語言的靈活運用能促進思維能力發展,同時也幫助學生形成符號意識.在結構化的幾何教學中,滲透符號意識的策略:①引導學生用符號語言表達圖形的性質(結構)和圖形之間的關系,從大概念的視角審視符號語言的作用,即幾何符號語言表達的是結構和關系;②符號語言中蘊含著基本圖形語言,是進行邏輯推理的工具和抓手,實際上就體現了符號語言的可操作性,從本質上和代數推理和變形原理是一致的,強調步步有據,這樣的教學就體現了符號語言的作用,讓學生從更高的視角理解幾何推理的本質,實現知識在不同情境下的正向遷移.

二、 在函數教學中用符號描述變化,強化符號的表達功能,促進符號意識形成

七年級的符號意識形成表現為用字母表示數,完成了從算術思維到代數思維的跨越,并且把符號作為對象參與運算,實現了符號的可操作性.在實際問題中引入符號(未知數)刻畫現實世界中的等量關系和不等關系,初步體會了代數思維的特點[1].八年級數學中很重要的內容就是一次函數與反比例函數,函數模型簡明扼要的把復雜的現實情境中的一類兩個變量的關系概括的清清楚楚,利用函數的圖像、表格及表達式等符號語言表達函數關系三類符號語言的相互轉化,促進學生符號意識的形成與深化理解,發展學生的抽象能力和建模能力[2],函數內容的結構化教學方法如下所示.

1.用符號表示函數關系,描述和解釋現實世界

從具體情境中抽象出兩個變量之間的關系與規律,是列函數表達式的基礎.而函數表達式同樣深刻揭示了一類問題中的共性和普遍性,學生運用表達式或圖像或表格解決問題則提升了學生對于符號的理解,進一步發展學生的數學抽象能力和數學建模能力.

案例2 蘇科版八年級上冊“6.2一次函數”.

問題1 給汽車加油的加油槍流量為25L/min．如果加油前油箱里沒有油,那么在加油過程中,用y(L)表示油箱中的油量,x(min)表示加油時間.

(1)y是x的函數嗎?如果是,請寫出函數表達式;

變式1 油的加油槍流量為40L/min．如果加油前油箱里沒有油,那么在加油過程中,用y(L)表示油箱中的油量,x(min)表示加油時間,y與x之間有怎樣的函數表達式?

(2)如果加油前油箱里有6L油,y與x之間有怎樣的函數表達式?

變式2 如果加油前油箱里有5L油,y與x之間有怎樣的函數表達式?加油前油箱里有8L油呢?

(3)如果加油后油箱里有油40L,每行駛100km耗油10L,寫出行駛過程中油箱內剩余油量Q(L)與行駛路程s(km)的函數表達式;

問題2 這些函數表達式有什么共同特點?

歸納：一般地,如果兩個變量x與y之間的函數關系,可以表示為y=kx+b(k、b為常數,且k≠0)的形式．那么稱y是x的一次函數(linearfunction).特別地,當b=0時,y叫做x的正比例函數．所以正比例函數是特殊的一次函數.

這是八年級上冊一次函數概念教學的片段,問題的設置蘊含了豐富的符號意識,用變量表達現實世界的變化,即兩個變量之間的關系,這是學生要經歷的第一次抽象的過程,而概括這些函數表達式的共同特點是讓學生再次經歷用符號來表示一次函數模型,是學生在概念形成前的第二次抽象.這些問題及其變式就是運用符號來培養抽象能力和建模能力的生活具象,是教學中不可或缺的重要環節.

2.用多種語言表征函數,促進符號表達的深刻理解

引導學生用多種語言表示函數:一種是數學內部與外部之間的轉化,即自然語言和函數的符號語言的轉化,第二種是數學內部間的互相轉化,即函數的不同表達方式之間的相互轉化,從而提高學生的符號意識,發展學生的多元表征意識.

案例3 蘇科版八年級上冊“6.3一次函數的圖像”.

觀察如圖2的圖片,并將你獲得的信息填入下表:

點燃時間/min05101520香的長度/cm

圖2

設燃燒過程中香的長度為y,燃燒時間為x,你能寫出y與x之間的函數表達式嗎?

以x軸表示香的燃燒時間,y軸表示香的長度,建立平面直角坐標系,畫出它的圖像.

很多一線教師在進行這節課的教學中常忽視此情境.實際上此現實情境能幫助學生深入理解自然語言所蘊含的香的長度隨著燃燒時間的變化而變化的含義,用不同的方式記錄香的長度:表格、表達式、函數圖像,讓學生體會到不同的符號語言的內在一致性,同時,讓學生感受到符號語言比自然圖片語言更具有一般性與概括性,更能表述函數的本質屬性.

教學策略：函數是表達現實世界規律和數量關系的又一重要模型,函數教學是符號意識形成的又一重要契機,在函數教學中促進符號意識形成有如下策略:①強化函數三種表示方法(函數表達式、圖表法、圖像法)的教學,同時揭示不同符號表達函數在本質上的一致性;②從三種符號表示方式的差異性上,理解每種表達方式的優缺點,特別是要強化函數圖像的教學,實踐證明學生在處理函數圖像有關問題還不能靈活和創造性應用.

三、在問題解決教學中引入符號,強化符號的操作功能,深化符號意識

符號語言不僅僅是數學交流和表達的工具,更是一種思維和操作的方式,也是發現問題和解決問題的工具,是代數思維的基礎.能夠使用符號進行運算推理,實現問題解決,是提升符號意識的一種可視化表現.

案例4 甲、乙兩運動員在長為100m的直道AB(A,B為直道兩端點)上進行勻速往返跑訓練,兩人同時從A點起跑,到達B點后,立即轉身跑向A點,到達A點后,又立即轉身跑向B點…若甲跑步的速度為5m/s,乙跑步的速度為4m/s,則起跑后100s內,兩人相遇的次數為( ).

A．5 B．4 C．3 D．2

方法1：分別計算每次相遇的時間(略).

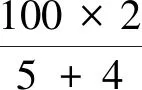
方法3：圖象法(如圖3):觀察圖象,兩人運動圖象交點有4個,兩人相遇4次.

三種解法是三種不同符號語言的表達,方法1是算術方法,方法2是構造方程模型,方法3用函數圖像來表示運動過程,直觀性強,問題解決有創新意識,是符號意識靈活運用的具體體現.這個問題還可以作變式,變化為甲乙兩人分別從A、B兩地同時起跑,這樣第一次相遇路程和為100m,問題會變得更加復雜,用圖像法來解決問題更具有優勢.

教學策略：問題解決是數學學習的重要環節,教學中要善于運用問題解決深化符號意識的形成.在問題解決中深化符號意識形成策略:①設置典型問題深化符號意識.八年級學生已經具備較強的邏輯推理能力,教學中可以設計有一定思維含量的綜合性問題,在問題解決中強化學生引入符號表達現實問題或數學問題的意識,引入參量解決問題是高中階段學習必需的技能,是符號意識形成的重要標志;②優化符號的表達方式,深化符號意識.數學表達不僅是解決問題的方式,更是認識問題的途徑,同一個問題用不同的表達方式,在最優化的符號表達中形成符號解決問題的深刻理解;③ 運用符號語言使問題解決程序化和操作化,深化符號意識.要引導學生看透形式符號背后的代數結構或者圖形結構,把解決問題的過程內化為“對象”,能對“對象”進行操作,提高解決問題的創新意識和創新能力.

在義務教育階段,數學眼光主要表現為:抽象能力(包括數感、 量感、符號意識)、幾何直觀、空間觀念與創新意識.會用數學的思維思考現實世界,表現為能夠運用符號運算、形式推理等數學方法,分析、解決數學問題和實際問題.會用數學的語言表達現實世界表現為:數據意識或數據觀念、模型意識或模型觀念、應用意識.通過經歷用數學語言表達現實世界中的簡單數量關系與空間形式的過程,學生初步感悟數學與現實世界的交流方式[3].可見學生符號意識形成與核心素養密切相關,隨著義務教育數學課程標準的頒布和實施,以核心素養立意的初中數學課堂教學改革必將向縱深的方向發展,初中生符號意識的形成其本身就是數學素養的重要組成部分,也是數學交流和表達的重要載體,初中生符號意識形成策略值得深入研究.