2023年高考三角函數經典問題聚焦
侯有岐(正高級教師 特級教師) 趙曉麗 張桃青
(陜西省漢中市四〇五學校)
2023年高考三角函數問題主要圍繞“五點法確定解析式、三角函數的定義、三角函數圖像與性質”等展開,注重考查圖像變換、單調性、奇偶性、周期性、對稱性、最值、零點等知識,并常與三角恒等變換等其他知識交會命題,難度中等.
1 “五點法”確定三角函數的解析式

圖1



總結 本題考查根據函數圖像求函數的解析式,從而解出函數值,熟練掌握三角函數的有關性質,以及特殊角的三角函數值是解題的關鍵.
1)根據y=Asin(ωx+φ)(x∈R)的圖像求函數解析式的步驟:
(1)確定振幅和周期,從而得到A與ω.
(2)A為離開平衡位置的最大距離,即最大值與最小值的差的一半.
(3)ω由周期得到:a)函數圖像在其對稱軸處取得最大值或最小值,且相鄰的兩條對稱軸之間的距離為函數的半個周期;b)函數圖像與x軸的交點是其對稱中心,相鄰兩個對稱中心間的距離也是函數的半個周期;c)一條對稱軸與其相鄰的一個對稱中心之間的距離為函數的個周期(借助圖像很好理解記憶).
(4)求φ的值時最好選用最值點,求峰點:ωx+);求谷點:(k∈Z);也可用零點求,但要區分該零點是上升零點,還是下降零點,上升零點(圖像上升時與x軸的交點):ωx+φ=2kπ(k∈Z);下降零點(圖像下降時與x軸的交點):ωx+φ=π+2kπ(k∈Z).
2)f(x)=Asin(ωx+φ)(A>0,ω>0)的圖像關于直線x=m對稱,則f(m)=±A;關于點(n,0)對稱,則f(n)=0.由函數y=Asin(ωx+φ)(x∈R)的圖像確定A,ω,φ的題型,常常以五點法中的第一零點(-,0)作為突破口,要從圖像的升降情況找準第一零點的位置,要善于抓住特殊量和特殊點.


答案 D.
2 三角函數的周期性和對稱性

方法2 因為f(x)=(x-1)2+ax+cosx=x2+(a-2)x+1+cosx為偶函數,所以a-2=0,解得a=2.
總結 關于函數奇偶性的幾個重要結論:
1)f(x)為奇函數?f(x)的圖像關于原點對稱;f(x)為偶函數?f(x)的圖像關于y軸對稱.
2)若函數f(x)是偶函數,則f(x)=f(|x|).
3)既是奇函數又是偶函數的函數只有一種類型,即f(x)=0(x∈D),其中定義域D是關于原點對稱的非空數集.
4)奇函數在兩個對稱的單調區間上具有相同的單調性,偶函數在兩個對稱的單調區間上具有相反的單調性.
5)偶函數在關于原點對稱的區間上有相同的最大(或最小)值,取最值時的自變量互為相反數;奇函數在關于原點對稱的區間上的最值互為相反數,取最值時的自變量也互為相反數.
6)設f(x),g(x)的定義域分別是D1,D2,那么在它們的公共定義域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶×偶=偶,奇×偶=奇.
7)復合函數的奇偶性可概括為:“同奇則奇,一偶則偶”.
注意 判斷分段函數的奇偶性應分別對每段函數證明f(-x)與f(x)的關系,只有當各段上的x都滿足相同關系時,才能判斷其奇偶性.
變式 (2023年天津卷5)已知函數f(x)的一條對稱軸為直線x=2,一個周期為4,則f(x)的解析式可能為( ).

答案 B.
3 三角函數的單調性和最值
例3 (2023年上海卷15)已知a>0,函數y=sinx在[a,2a]上的最小值為s,在[2a,3a]上的最小值為t,則下列不可能的是( ).
A.s>0且t>0 B.s<0且t<0
C.s>0且t<0 D.s<0且t>0
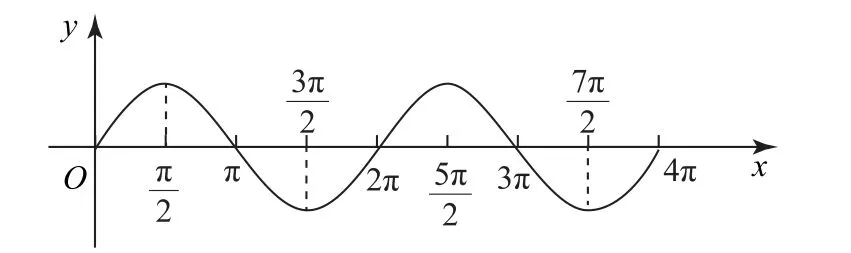
圖2

綜上,選D.
總結 要想判斷正弦函數在相鄰區間上函數值的正負,只要熟練作出函數的圖像,在給定的區間上取特殊值檢驗判斷,本題實質考查正弦函數在所給相鄰區間上的單調性和值域.
變式 (2023 年北京卷13)已知命題p:若α,β為第一象限角,且α>β,則tanα>tanβ.能說明p為假命題的一組α,β的值為α=_________,β=_________.
4 三角函數圖像變換

圖3



總結 三角函數圖像變換問題要先利用三角變換(誘導公式、降次輔助角公式等)將不同名三角函數轉換成同名三角函數.同名三角函數圖像的變換有兩種途徑:一是先伸縮再平移,二是先平移再伸縮.
特別注意:y=Asin(ωx+φ1)到y=Asin(ωx+φ2)的平移單位
當Δx>0時,是將y=Asin(ωx+φ1)圖像上所有點向左平移Δx個單位;
當Δx<0時,是將y=Asin(ωx+φ1)圖像上所有點向右平移-Δx個單位.
變式 (2022 年浙江卷6)為了得到函數y=2sin3x的圖像,只要把函數)圖像上所有的點( ).

答案 D.
5 三角函數的零點
例5 (2023年新高考Ⅰ卷15)已知函數f(x)=cosωx-1(ω>0)在[0,2π]上有且僅有3個零點,則ω的取值范圍是_________.

因為0≤x≤2π,ω>0,所以0≤ωx≤2ωπ,令f(x)=cosωx-1=0,則cosωx=1有3個根.令t=ωx,則cost=1 有3 個根,其中t∈[0,2ωπ],結合余弦函數y=cost的圖像(如圖4)及性質可得4π≤2ωπ<6π,故2≤ω<3.

圖4
總結 三角函數的零點問題常常化歸為三角函數圖像與直線的交點問題,然后利用函數圖像數形結合地探究范圍,主要考查三角函數的圖像變換、單調性、對稱性、周期性等.
1)三角函數的奇偶性:
函數y=Asin(ωx+φ)是 奇 函 數?φ=kπ(k∈Z),偶函數
函數y=Acos(ωx+φ)是奇函數(k∈Z),偶函數?φ=kπ(k∈Z).
函 數y=Atan(ωx+φ)是 奇 函 數?φ=kπ(k∈Z).
2)三角函數的對稱性:
函數y=Asin(ωx+φ)的圖像的對稱軸可由解得,對稱中心的橫坐標可由ωx+φ=kπ(k∈Z)解得.
函數y=Acos(ωx+φ)的圖像的對稱軸可由ωx+φ=kπ(k∈Z)解得,對稱中心的橫坐標可由)解得.
函數y=Atan(ωx+φ)的圖像的對稱中心的橫坐標可由解得.
變式 (2022年全國乙卷理15)記函數f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期為T,若為f(x)的零點,則ω的最小值為_________.
答案 3.
6 函數圖像與解析式的匹配
例6 (2023年天津卷4)函數f(x)的圖像如圖5所示,則f(x)的解析式可能為( ).

圖5
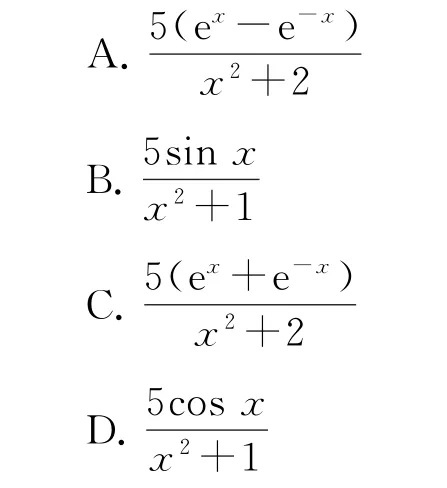

由圖像可知f(x)圖像關于y軸對稱,f(x)為偶函數,故A,B錯誤.對于選項C,當x>0時,恒大于0,與圖像不符合,所以C錯誤,故選D.
總結 本題考查了函數圖像的識別,解題的關鍵是掌握識別圖像的方法,一般可從定義域、值域、函數值的正負、特殊點、特殊值、函數的性質等方面進行判斷,考查了直觀想象能力與邏輯推理能力.
變 式 (2021 年 浙江卷7)已知函數f(x)=,則圖像為圖6 的函數可能是( ).

圖6

答案 D.
7 三角函數同數列及集合的交會


綜上,選B.
總結 本題是集合、數列、三角函數的綜合題,對等差數列、集合的概念、三角函數的周期性進行了深入的考查,同時,考查了數學抽象、邏輯推理等數學核心素養.求解通項中含有以n為變量的三角函數的數列問題,如含有等形式的數列,通常先求出三角函數的周期性,再研究數列在一個周期內的項的規律.
變式 設集合M={y|y=|cos2x-sin2x|,x∈R},,i為虛數單位,x∈R},則M∩N為( ).
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
答案 C.
8 三角換元和輔助角公式
例8 (2023年全國乙卷文11)已知實數x,y滿足x2+y2-4x-2y-4=0,則x-y的最大值是( ).
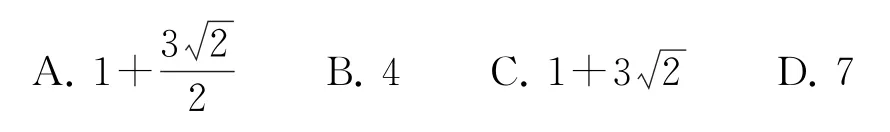

方法1 令x-y=k,則x=k+y,代入原式化簡得
因為實數y存在,則Δ≥0,即(2k-6)2-4×2(k2-4k-4)≥0,化簡得k2-2k-17≤0,解得1-3 2≤k≤1+3 2,則x-y的最大值是3 2+1,故選C.
方法2 將x2+y2-4x-2y-4=0整理得
令x=3cosθ+2,y=3sinθ+1,其中θ∈[0,2π],則
總結 本題的實質為圓上的動點的橫、縱坐標之差的最值,方法1設元構造平行的直線系與圓恒有交點,借助一元二次方程的判別式求解;方法2 通過三角換元,利用余弦函數的有界性求解;方法3 設元構造平行的直線系與圓恒有交點,利用圓心到直線的距離小于或等于半徑解出最值.方法2凸顯了三角函數的工具性,方法1和方法3凸顯了直線與圓相交的幾何性質的應用.
變式 (2022年新高考Ⅱ卷12,多選題)若x,y滿足x2+y2-xy=1,則( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1
答案 BC.
9 三角函數開放性探索問題
例9 (2023 年北京卷17)設函數f(x)=

注:如果選擇的條件不符合要求,第(2)問得0分;如果選擇多個符合要求的條件分別解答,按第一個解答計分.

(1)因為f(x)=sinωxcosφ+cosωxsinφ,所以
(2)因為f(x)=sinωxcosφ+cosωxsinφ=,所以f(x)的最大值為1,最小值為-1.
若選條件①:因為f(x)=sin(ωx+φ)的最大值為1,最小值為-1,所以無解,故條件①不能使函數f(x)存在.

三角函數是高中數學核心內容之一,也是高考重點考查的內容,此類問題大多為中檔題,難度不大.只有抓住概念的本質,回歸原點,把數學思想方法貫穿于教學始終,才能提高學生的思維水平,培養學生的能力,提升學生的素養,從而適應考試題目的創新.
(本文系陜西省第四批基礎教育教學名師培養工作專項課題?“三新”背景下農村高中生數學運算素養培養的策略研究?(編號:SJS2022RZ077)的階段性研究成果.)
(完)

