基于AHP-EWM-TOPSIS模型的電梯品牌評價方法

李 恒 趙金強 王新慧 丁彥龍 吳占穩

（中國特種設備檢測研究院 北京 100029）

根據國家市場監督管理總局特種設備安全監察局發布的關于2022年全國特種設備安全狀況的通告，截至2022年底，全國范圍內的各類電梯總數已達964.46萬臺。分析近年來的數據可知，我國的電梯數量基本上是每年以10%左右的速度增長，電梯業的高速發展給使用單位、銷售單位、安裝單位、維護保養單位以及特種設備安全監察機構等各方均帶來了新的命題[1]。雖然國內大部分省份均出臺了指導電梯選型配置的法規標準，并且部分省市公布的電梯安全管理條例或辦法也對電梯的選型做了要求，但僅僅是出于安全的考慮，對某些裝置或配件配備作出要求，不能有效地指導電梯品牌的選擇。特別是開發商在新建樓盤選擇電梯品牌時，面對質量、價格、安全系數、售后服務能力、乘坐舒適感多個影響因素時，很難找到一個能夠平衡各方需求的選擇方案[2]。

本文在綜合調研分析影響電梯品牌因素的基礎上，利用層次分析法的理念建立評價體系。同時為有效避免單一賦權法的不足，使用主觀和客觀綜合賦權的方法綜合確定各指標的權重，形成了一種基于綜合權重的評價方法，即AHP-EWM-TOPSIS法[3]。并進行實例驗證，構建評價體系，包含4個一級評價指標、20個二級評價指標，實例結果表明該評價方法可靠有效[4]。

1 基于AHP-EWM-TOPSIS模型新裝電梯品牌選擇評價方法

在綜合評價工作中，幾乎所有人員都會把指標權重的確定看作是整體過程中的核心內容，對評價的有效性起決定性作用。常見的指標權重確定方法分為兩類：1）主觀賦權法，主要包括德菲爾法、序關系分析法以及層次分析法等；2）客觀賦權法，有主要成分分析法、離差及均方差法和熵權法等。為保證評價的可靠性，采用行業內評價結果較為可靠的層次分析法確定主觀權重，利用熵權法確定客觀權重，再求得綜合權重，最后利用貼近理想解法確定方案的優劣程度，得到評價方案的綜合排序，指導實際應用[5]。

1.1 評價體系建立

調研行業內相關方的專家，綜合各方意見，確定影響評價方案的主要因素，利用層次分析法的原理及各因素之間的關聯關系，將有相關特征的因素歸納成組，并根據因素的影響關系逐級分層，確定評價的層次模型，最高層為目標層、中間為準則層、最底層為方案層[6]。

1.2 基于AHP法+EWM法指標權重確定

主觀賦權法雖然發展較早，能夠綜合考慮專家經驗和評價者的目的，但是主觀性太強，很難保證評價的科學性；客觀賦權法采用定量分析問題的方法，具有較強的數學理論依據，減少評價人員的主觀臆斷性，但是容易忽略專家的意見及使用方的需求。綜合2種方法的優缺點，平衡評價工作者的主觀偏好以及評價的目的性，采用組合賦權的方法，加強評價結果的可靠性[7]。同時考慮到AHP法和EWM法在行業內使用的普遍性及適用性，本文采用將兩者結合，確定評價指標的權重。

●1.2.1 AHP法確定主觀權重

AHP法在決策分析時，可將一個由諸多因素構成的相互關聯、相互制約的復雜方案，從不同角度進行評價，是一種定性與定量相結合的分析方法，能夠實現將復雜的決策問題簡便化[8]。其原理是對目標問題進行分解，構建層次結構模型，進而對決策問題的影響因素進行關聯比較必要性，在對各方案進行一致性檢驗之后，實現對目標問題的權重確定。具體步驟如下：

1）構建判斷矩陣

為獲得各個評價層級指標的權重，利用1-9標度法，組織涉及電梯行業的住建、制造、使用、安裝、維保、檢驗及監察等方面的專家，分別對準則層以及方案層的同階層相鄰兩個指標進行比較打分賦值，構建判斷矩陣，記為A，其中：

式中：

aij——第i個指標的重要性與第j個元素重要性的比值，賦值標準見表1。

表1 1-9標度法賦值標準[8]

2）計算特征向量和最大特征值并進行一致性檢驗

（1）利用和積法將判斷矩陣按列歸一化，得到cij：

（2）將歸一化的矩陣按行求和，得到ri：

（3）計算矩陣特征向量的近似值ωi：

（4）計算特征向量ωi的最大特征值λmax：

式中：

（Aω)i——Aω的第i個元素。

（5）判斷矩陣主要是依據專家組的評判結果構成，存在一定的主觀性，為了使判斷矩陣的元素比例分配更為合理，需對矩陣進行一致性檢驗，首先計算一致性指標CI：

其次，再計算單次一致性比率CR單，其中指標RI的數值選取見表2。

表2 隨機一致性指標RI對照表

當CR單＜0.10時，滿足一致性檢驗的要求，否則認為矩陣未通過一致性檢驗，需要重新構造判斷矩陣和打分取值，直至滿足一致性要求。

3）層次總排序及一致性檢驗

為避免評價指標各層次經過單排序一致性檢驗后，存在非一致性累加現象，層次的總排序也需要進行一致性檢驗，與層次單排序的一致性檢驗方法相同，計算層次總排序的一致性比率CR總，若CR總＜0.10，滿足一致性檢驗要求，其中：

式中：

CIj——單排序一致性指標；

RIj——相應的平均隨機一致性指標；

aj——方案層矩陣的特征向量值。

通過一致性檢驗后，然后利用方案層各個指標的權重乘以準則層的權重，可得到方案層對總目標的主觀權向量，記為ωA。

●1.2.2 EWM法確定客觀權重

EWM法，是評價工作中常用的一種客觀賦權法。按照信息論原理解釋，熵是系統無序程度的一個度量，可以利用熵值評價方案中某個指標的離散程度，其熵值越小，指標的離散程度越大，該指標對綜合評價的影響程度就越大。因此，可利用熵計算出各個指標的權重，為多指標綜合評價提供依據。具體步驟如下：

1）構建評價矩陣

假設此評估方案中包含m個樣本，分別有n個指標，建立原始評估矩陣E，記為E=（eij）mn，其中eij表示第i個樣本的第j個指標值。

2）數據歸一化處理

對評價矩陣進行無量綱化、標準化處理，效益型指標和成本型指標分別選擇正向和負向指標。如果在數據處理過程中出現數值為0，為最大限度地維護原始矩陣評價的有效性，需對數據整體向右平移，即eij＋0.000 1。

式中：

——矩陣E的正向指標；

——矩陣E的負向指標。

3）計算指標權重

（1）計算第j個樣本下第i個指標的特征比重pij：

（2）計算第j項指標的熵值qj：

（3）計算各評價指標的權重ωE：

●1.2.3 確定綜合權重

AHP法在計算權重的過程中，主要依據評價工作者的主觀經驗，得到的結果具有較強的貼合實際需求性，但是同時也會由于主觀因素的原因帶來偏差[9]。EWM法可以充分利用數據本身所包含的原始信息，得到較為客觀的評價結果，但是不能反映評價工作者的經驗和客戶的意見。組合賦權的前提是要保證單一賦權法結果的有效性，同時較好互補2個評價方法的劣勢，求得一個合理的綜合權重，本文采用拉格朗日乘子法計算組合權重ωAE，即

1.3 基于綜合權重的TOPSIS法的評價模型

TOPSIS法是評價工作中常用的一種多目標決策分析方法，原理是基于權重確定多決策目標的正理想解和負理想解的距離，然后對評價方案進行排序，若評價對象距離最優解最近又遠離最劣解即為最優方案[10]。具體步驟如下：

1）構造規范化矩陣

假設此評估方案包含m個樣本，分別有n個指標，構造原始評價矩陣，T=（tij)mn，評估中專家在確定權重時，已組織進行了打分，即可認為矩陣T=E，然后對矩陣進行加權規范化處理，得到規范化矩陣zij，即：

2）確定正負理想解

正理想解A+j和負理想解A-j的計算式如下：

3）計算歐式距離

采用空間歐式距離分別計算樣本指標與正理想解Di+及負理想解Di-的距離：

4）確定貼近度Fi

計算各方案與理想解的相對接近度，根據Fi值的大小進行排序，Fi越大，方案越優。

2 實例應用

2.1 評價指標體系構建

本文依據特種設備安全的法律法規、電梯質量安全相關的規范和質量管理的理論和要求，借鑒以往的學者對電梯品牌和質量安全研究的理論基礎，同時調研行業內相關呼聲以及使用單位的意愿，建立新裝電梯的品牌選擇的評價體系。影響電梯品牌選擇的主要因素包括制造安裝單位的綜合能力、電梯主要系統的安全水平、使用周期內使用單位需要承擔的基本費用以及電梯使用的體驗感等方面[11-12]。根據這4個模塊技術特點以及影響因子，構建評價指標體系，最終形成4個一級指標和20個二級指標，如圖1所示。

圖1 評價指標體系

為了保證評價指標的有效性和合理性，通過網絡查詢、電話訪談以及實地走訪調研行業內電梯品牌，根據市場需求，協調組織電梯制造單位、使用單位、維護保養單位、監管單位及檢驗檢測單位的相關專家組成專家團隊，按照既定的電梯品牌綜合評價結構，對常見的5個電梯品牌方案層的所有指標進行打分，結果見表3。

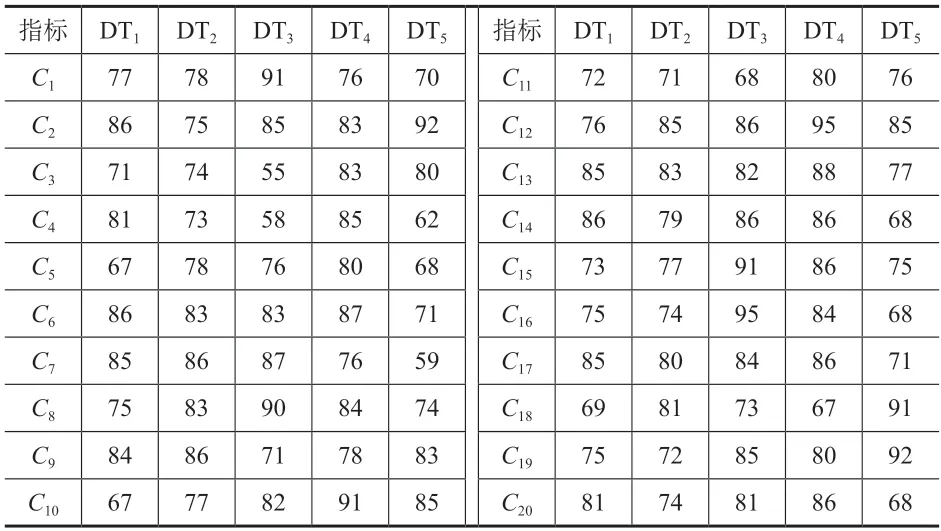
表3 不同電梯品牌評價指標打分結果

2.2 計算指標權重

1）AHP法計算指標主觀權重

組織專家分別對準則層以及方案層同階層的相鄰兩個指標進行比較打分賦值，構造目標層、準則層及方案層各因素的判斷矩陣。A-B、B1-C、B2-C、B3-C以及B4-C判斷矩陣分別如下所示。

根據式（2）～式（7）計算得到A-B矩陣的最大特征值λmax=4.046 0，CI=0.015 3，RI=0.9，CR=0.017 0＜0.1，滿足一致性檢驗，則權重矩陣ωA=（0.110 5 0.250 2 0.417 0 0.222 4)T可接受。同理可得到：

（1）B1-C矩陣：λmax,B1=4.045 8，CIB1=0.015 3，RIB1=0.9，CRB1=0.017 0＜0.1，ωB1=（0.097 2 0.183 6 0.286 7 0.432 5)T；

（2）B2-C矩陣：λmax,B2=8.215 5，CIB2=0.030 8，RIB2=1.41，CRB2=0.021 8＜0.1，ωB2=（0.051 4 0.129 7 0.059 4 0.086 1 0.112 1 0.182 2 0.136 6 0.242 6)T；

（3）B3-C矩陣：λmax,B3=4.010 4，CIB3=0.003 5，RIB3=0.9，CRB3=0.003 8＜0.1，ωB3=（0.109 3 0.189 2 0.350 7 0.350 7)T；

（4）B4-C矩陣：λmax,B4=4.096 6，CIB4=0.032 2，RIB4=0.9，CRB4=0.035 8＜0.1，ωB4=（0.100 1 0.311 1 0.182 4 0.406 4)T。

根據式（8）計算得到CR總=0.017 5＜0.1，通過一致性檢驗，然后利用方案層各個指標的權重乘以準則層的權重，得到所有方案層對總目標的權向量，記為ωA=（0.010 7 0.020 3 0.031 7 0.047 8 0.012 9 0.032 4 0.014 9 0.021 5 0.028 0 0.045 6 0.034 2 0.060 7 0.045 6 0.078 9 0.146 2 0.146 2 0.022 3 0.069 2 0.040 6 0.090 4)T。

2）EWM法計算指標主觀權重

根據式（9）～式（13）計算得到各評價方案的熵值以及權重，另外要特別說明的是，在計算正負理想解距離時，C1～C12、C18及C19為效益型指標，按照正理想解來計算；C13～C17及C20為成本型指標，按照負理想解來計算，得到各方案層指標的熵值qj及權重ωE見表4。

表4 利用EWM法計算的各方案層指標的qj及ωE值

3）確定綜合權重

通過式（14）利用拉格朗日乘子法求得組合權重ωAE，即ωAE=（0.025 2 0.029 2 0.035 3 0.053 8 0.029 4 0.034 6 0.023 9 0.039 2 0.033 9 0.044 3 0.044 4 0.052 1 0.048 9 0.096 5 0.084 6 0.079 1 0.047 3 0.074 7 0.050 7 0.072 9)T。

2.3 基于綜合權重的TOPSIS法電梯品牌選擇方法

按照式（15）對各評價方案的初始值進行規范化處理，再按照式（16）～式（20）計算各評價指標的正負理想解及歐式距離，比較其相對貼近度，結果見表5。

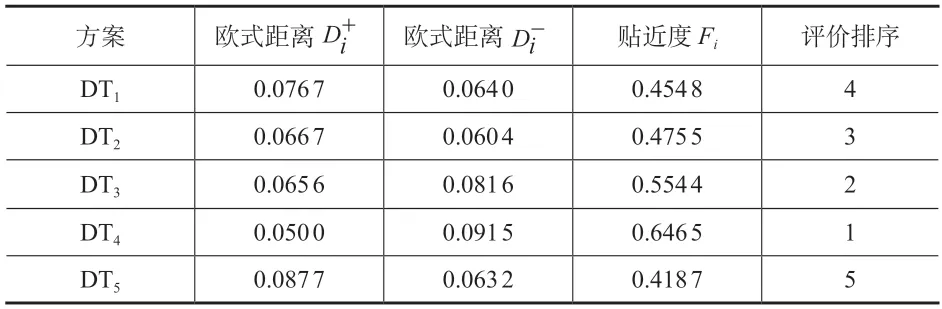
表5 正負理想解歐式距離與相對貼近度

通過比較各評價方案與正負理想解的相對貼近度，得到各電梯品牌的綜合指標的排序，依次為DT4＞DT3＞DT2＞DT1＞DT5，方案4的評價結果最優，方案5的評價結果最差。

從綜合權重可知，占比較高的幾個指標按照順序依次是年度維保費用C14（0.096 5)＞主要易損件費用C15（0.084 6)＞安裝驗收費用C16（0.079 1)＞困人停梯率C18（0.074 7)＞故障排除難易度C20（0.072 9)＞安全保護系統C12（0.052 1)＞設備使用年限C19（0.050 7)。

根據規范化矩陣的計算過程可知，方案4在上述7項占比較高的指標中有3項得分為第一，可作為新建樓盤電梯采購的備選方案；反觀方案5有4項得分倒數第一。

3 結論

1）通過AHP法的基本原理構建電梯品牌評價的指標體系，從制造安裝單位的綜合能力、電梯主要系統的安全水平、使用周期內需要承擔的基本費用以及使用的體驗感4個方面確定影響方案的20個評判指標。為保證評價結果的有效性，通過主觀權重和客觀權重結合，得出綜合權重，保證指標權重分配合理，避免僅靠少數指標進行評價的局限性。

2）通過綜合權重與TOPSIS法相結合的方法，既避免了單一因素帶來的決策失誤，也發揮了貼近理想解法能對多指標的相對優劣做出排序的優勢，做出更科學、全面、準確的評價。

3）基于AHP-EWM-TOPSIS法的電梯品牌綜合評價方法對新裝電梯的品牌選擇具有指導意義，可作為招投標或決策時的理論依據，也為其他類設備的品牌選擇提供了一種新的系統工程決策方法，同時也對住建部門以及特種設備安全監察部門對新裝電梯的安全監管工作有一定的支持。