基于自適應趨近律的對稱六相PMSM調速系統

劉陵順，李永恒，葛寶川

（1.海軍航空大學，山東 煙臺 264001；2.92781部隊，海南 三亞 572029）

0 引言

傳統PI 控制策略無法擺脫對電機模型和參數的依賴，難以滿足艦船、飛行器等軍事裝備對電機高性能控制算法的要求，因而具有一定的局限性。為提高電機控制性能，國內外學者提出諸多高性能控制算法[1]。其中，滑模變結構控制算法對外部干擾及內部參數變化具有不敏感性和極好的魯棒性，控制算法簡單，動態性能優異，能夠較好地滿足軍事裝備對電機高性能控制算法的要求。此外，它還具備動態響應速度快、諧波含量低、滑動模態下自適應性強、穩定范圍寬等優點。

這種算法自身也存在缺點。在理想狀態下，電機控制系統在結構控制力度無限強、切換頻率無限大時不會產生抖振。但實際情況下，受到切換開關不理想以及各種動作延遲等因素影響，系統切換頻率無法達到無限大，導致電機控制系統產生抖振。高為炳為克服滑模運動抖振問題，提出指數趨近律方法。通過調節趨近律參數，增強電機控制系統動態性能，減小抖振，但指數趨近律方法無法從根本上消除系統抖振[2-6]。

本文提出1種適用于九開關變換器驅動的對稱六相PMSM 調速系統的基于自適應趨近律的滑模控制方法，以此來進一步提高系統響應速度和抑制系統抖振問題。該自適應趨近律綜合冪次趨近律和變速趨近律優點，隨著系統狀態變量自適應調節滑模面參數，直至系統狀態軌跡運行到穩定點。當系統出現有界外部干擾時，系統狀態及其導數可快速收斂到平衡點附近的鄰域內。

1 基于自適應趨近律的對稱六相PMSM 調速控制器設計

1.1 對稱六相PMSM數學模型

對稱六相PMSM 物理模型中的轉子結構為表貼式，每相繞組的相位兩兩互差60°，其轉子物理模型結構如圖1所示[7]。

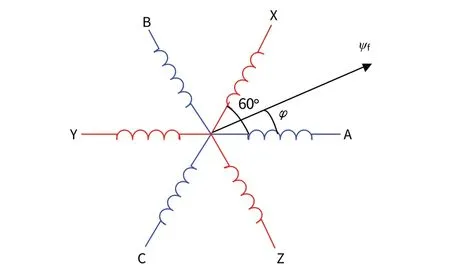
圖1 對稱六相PMSM電機結構圖Fig.1 Structure of symmetrical six-phase PMSM

為了滿足本文研究需要，作出如下假設：

1）對稱六相PMSM 電機轉子結構上沒有阻尼繞組；

2）研究過程中忽略定子、轉子鐵心磁阻；

3）研究過程中不考慮磁滯損耗和渦流損耗；

4）勵磁磁場和電樞反應磁場在氣隙中都是按照正弦規律分布的。

本文采用id=0 的轉子磁場定向控制策略，建立對稱六相PMSM 電機在dq 坐標系中的電機數學模型，可得對稱六相PMSM定子電壓方程為：

式（1）中：ud、uq為d、q 軸上的電壓分量；id、iq為d、q 軸上的電流分量；Rs為定子電阻；Ld、Lq為d、q 軸定子電感；ωe為轉子電角速度；ψf為轉子磁鏈。

本文采用磁場定向控制策略，即id=0，此時d、q坐標系下的電磁轉矩表達式為：

式（2）中：Te為電機電磁轉矩；p 為電機的極對數。

電機數學模型中的運動方程為：

式（3）中：TL為負載轉矩；J 為轉動慣量；ωm為轉子機械角速度；B 為阻尼系數。

將式（2）（3）聯立可得電機數學模型中的機械運動方程為：

1.2 控制器設計

設計滑模控制器的首要步驟在于尋找合適的滑模面；然后，在滑模面的基礎上設計控制器。

根據式（4），設計電機調速系統二階狀態空間方程為：

式（5）中：系統狀態變量x1=ωref-ωm，ωref為電機參考機械角速度；系統狀態變量x2=x˙1=-ω˙m；控制作用u=i˙q。理想條件下，一般認為負載轉矩TL為恒定值，即T˙L=0。但在實際應用PMSM時，負載轉矩TL是不斷變化的，尤其在負載突變時，不能簡單地把負載轉矩TL認定是恒值。

對于滑模控制器來說，線性滑模面是最常用的幾種滑模面之一。設計線性滑模面：

式（6）中：s 為線性滑模面函數；c 為滑模面比例系數。對式（6）進行求導，可得：

將式（7）整理，可得控制作用u 為：

對式（8）等式兩端分別求積分，可得：

在冪次趨近律[8-10]和變速趨近律[11]基礎上，提出了1種自適應趨近律[12]：

式（10）中：k1＞0 ；α ＞0 ；ε′=k2tansig |x |，k2＞0 ，

將式（10）代入式（9），得：

系統控制器輸出包含積分環節，可以消除穩態誤差，提高系統精度。但采用式（6）的線性滑模面，系統容易受到負載轉矩突變的影響。根據式（5），當負載轉矩TL突變時，負載轉矩變化量T˙L突變為較大值，進而影響調速系統二階狀態空間方程的穩定性，不利于控制器設計。

基于上述原因，設計積分滑模面：

對式（12）進行求導，可得：

將式（13）整理，可得控制器輸出iq為：

將式（10）代入式（14），得：

式（15）為基于自適應趨近律的對稱六相PMSM調速系統控制器輸出。iq作為電機q 軸電流控制器輸入的給定值，電機實際電流通過跟蹤控制器輸入給定值，進而輸出q 軸電壓uq。

設計q 軸電流控制器積分滑模面為：

式（16）中，eq=iq-iq1，iq1是電機定子六個相電流按照矢量空間解耦變換的q 軸上的電流分量，c1＞0。

對式（16）求導，并將式（1）代入，可得：

將式（10）代入式（17），可得：

由式（18）可以求得電流控制器q 軸上的輸出電壓為：

同理，設計d 軸電流控制器積分滑模面為：

式（20）中，ed=-id1，id1為電機定子的六個相電流按照矢量空間解耦變換的d 軸上電流分量，c2＞0。

對式（20）求導，并將式（1）代入求導后的式（20），可得：

將式（10）代入式（21），得：

由式（22）可以求得電流控制器d 軸上的輸出電壓為：

式（23）（19）分別為電流控制器d、q 軸上的輸出電壓。將電流控制器d 、q 軸輸出電壓由dq 變換到αβ 坐標系，可得α、β 軸電壓。

2 仿真結果分析

圖2為本文研究的九開關變換器的拓撲結構。九開關變換器的結構包含3 個橋臂，每個橋臂包含3 個IGBT開關管，共有9個開關管（S1～S9）。

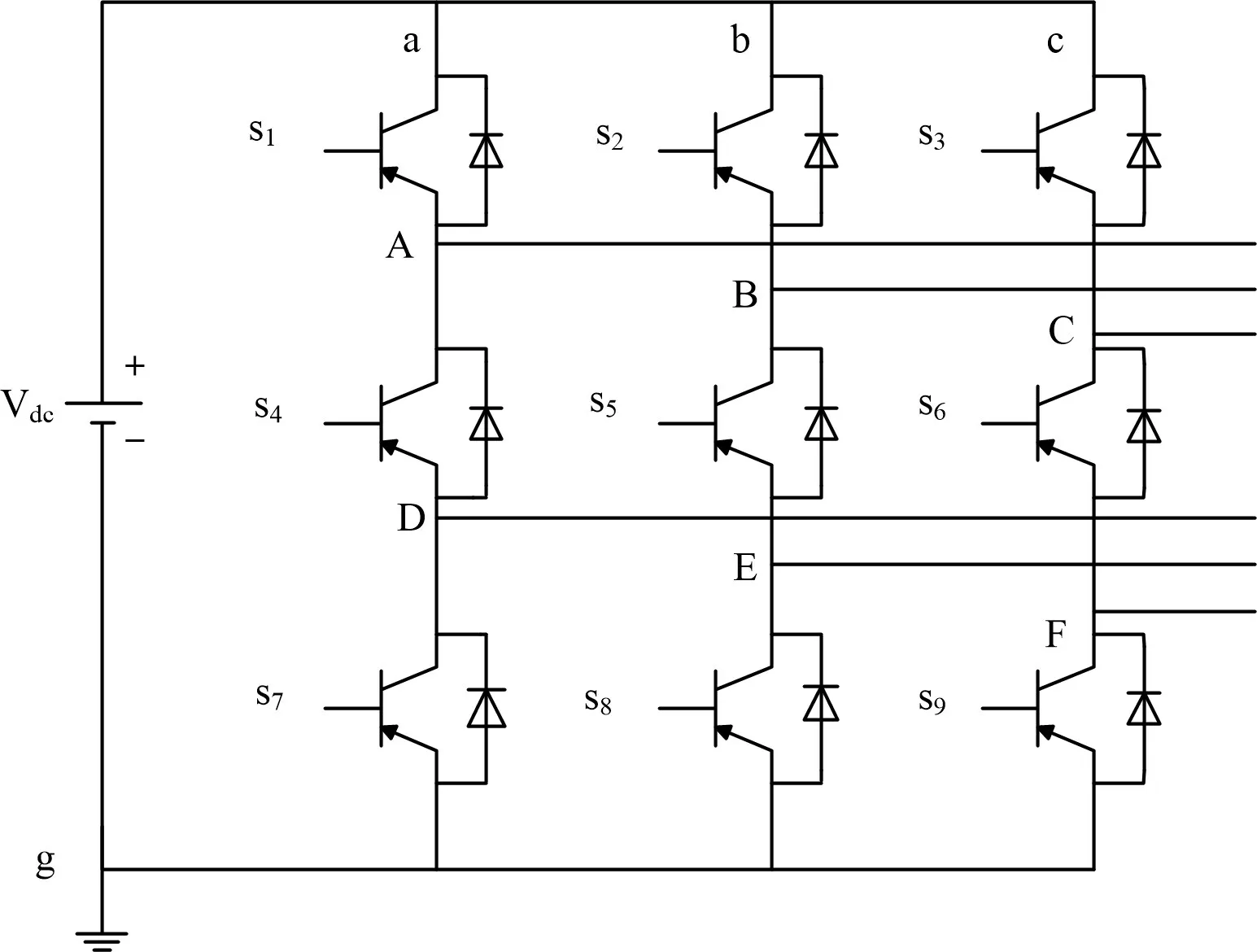
圖2 九開關變換器拓撲結構Fig.2 Nine-switch converter topology

其中：S1、S2、S3為上側開關管；S4、S5、S6為中間開關管；S7、S8、S9為下側開關管。上側開關管和中間開關管組成上側換流器；中間開關管和下側開關管組成下側換流器。九開關變換器對中間開關管進行了復用，能夠減少開關數量，減輕變換器的質量和縮小變換器的體積[13-15]。

中間開關管的通斷是由上、下側開關管決定的，并且上、下側開關管的通斷滿足異或關系：即上側開關管工作時，中間開關管工作，下側開關管不工作，此時，九開關變換器的上側換流器工作，下側換流器不工作；下側開關管工作時，中間開關管工作，上側開關管不工作，此時，九開關變換器的下側換流器工作，上側換流器不工作。為了滿足直流母線電壓不能短路的條件，有效的開關信號僅有3種，本文以a橋臂為例進行情況說明，如表1 所示。研究過程中不考慮開關的死區。本文以a橋臂來說明開關狀態與輸出電壓的情況：上側開關管S1和中間開關管S4的導通與斷開共同決定電壓UAg；中間開關管S4和下側開關管S7的導通與斷開共同決定電壓UDg。

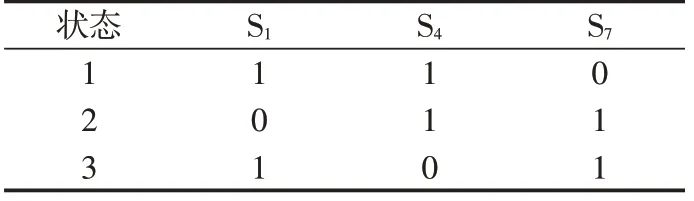
表1 九開關變換器a橋臂開關狀態Tab.1 A-phase bridge arm switch status of nine-switch converter

為了驗證基于自適應趨近律的對稱六相PMSM調速系統有效性，在MATLAB/Simulink平臺搭建電機驅動模型，如圖3 所示。對稱六相PMSM 的電參數如下所示：定子電阻Rs=1 Ω，定子漏感Ld=4.6 mH，轉子磁鏈Ψf=0.1 Wb，轉動慣量J=0.02 g·m2，極對數p=2 ，負載轉矩TL=1 N·m ，直流側母線電壓Vdc=300 V。

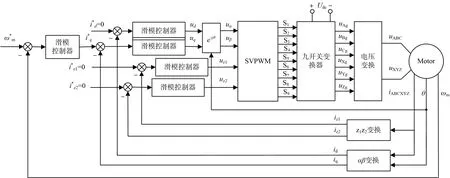
圖3 電機調速系統框圖Fig.3 Block diagram of motor speed control system

將基于自適應趨近律電機調速系統與基于指數趨近律電機調速系統[16-18]進行比較，可得系統啟動后的轉速、電磁轉矩、電流iq以及A 相電流波形，如圖4所示。系統啟動后的電壓uα、uβ以及電流iα、iβ波形如圖5 所示。其中，滑模面參數c=5，指數趨近律參數k=10，ε=5，自適應趨近律參數k1=10，k2=5，α=1.2。

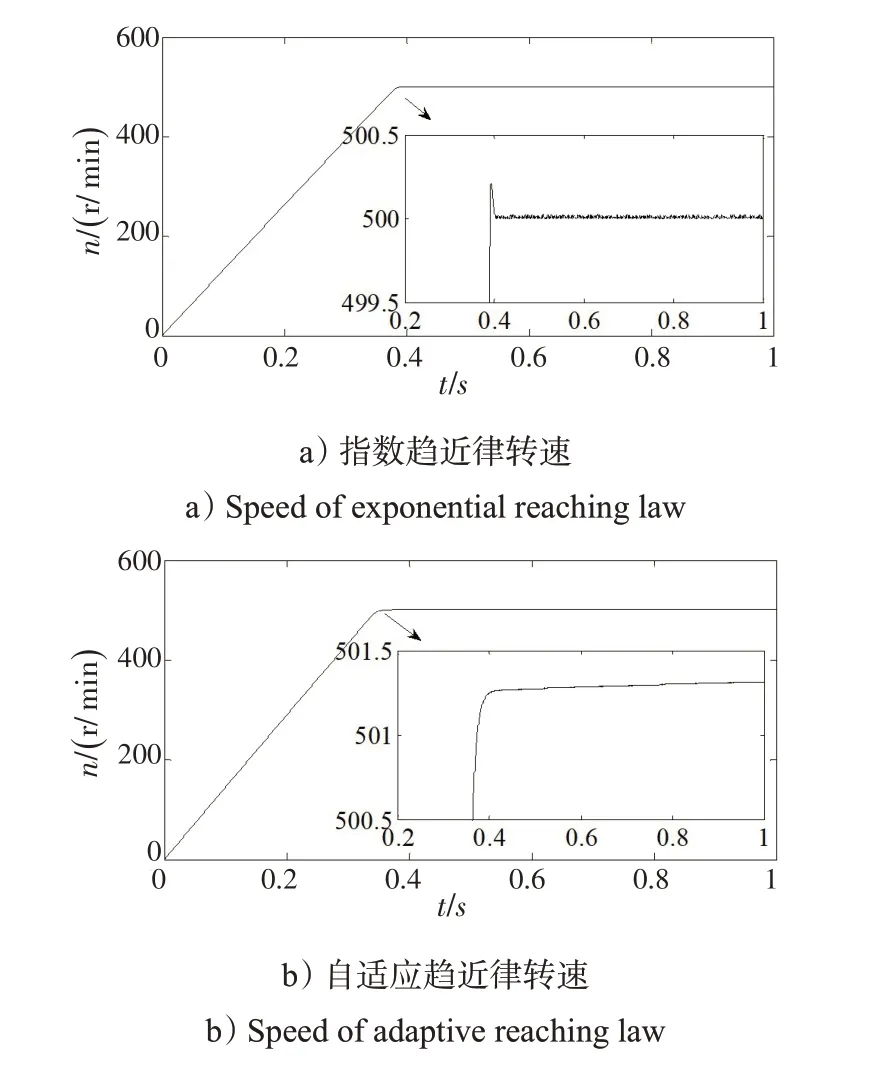
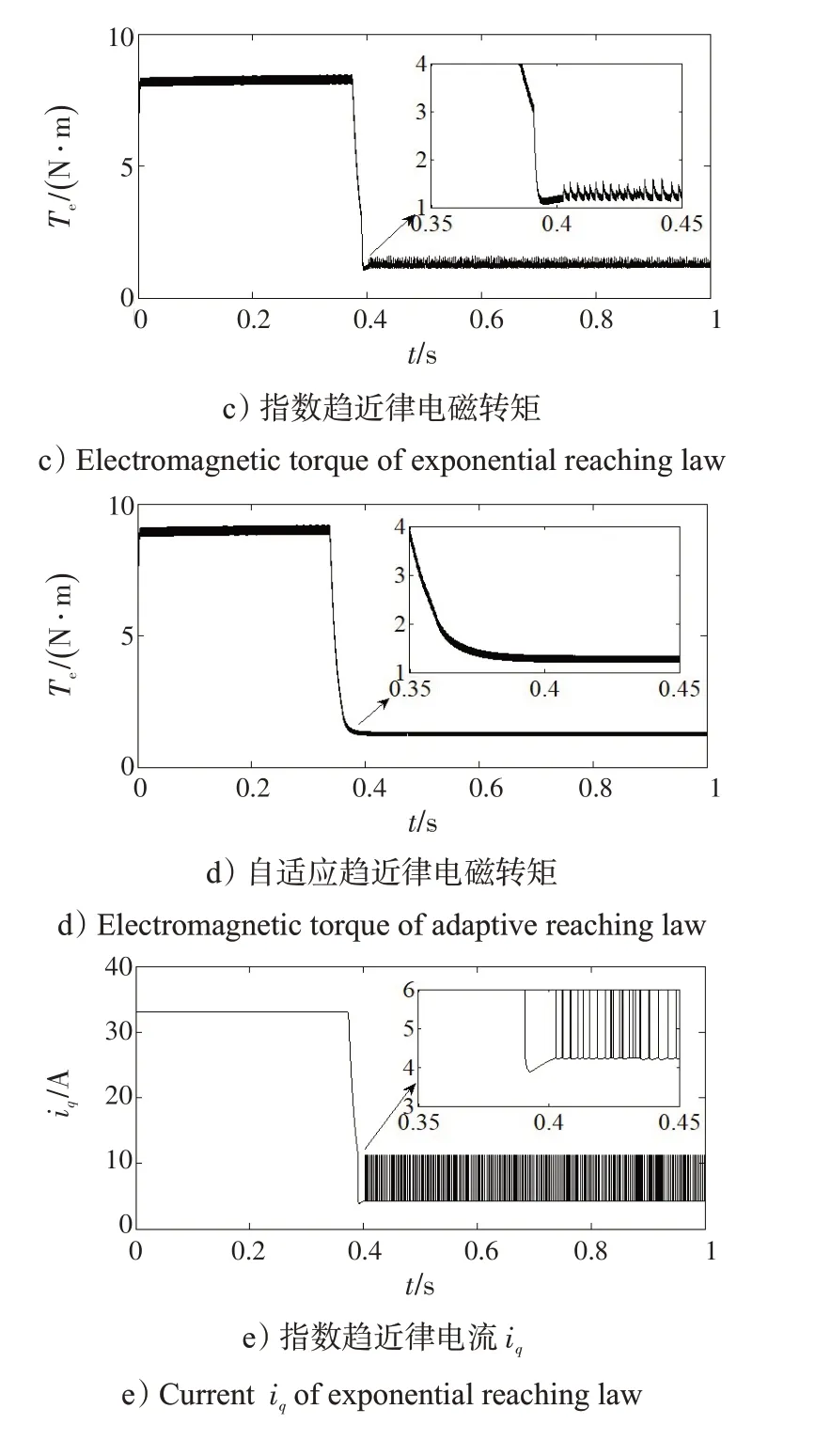
圖4 電機轉速、電磁轉矩、電流iq 以及A相電流波形比較Fig.4 Waveform comparison of motor speed,electromagnetic torque,current iq and A-phase current

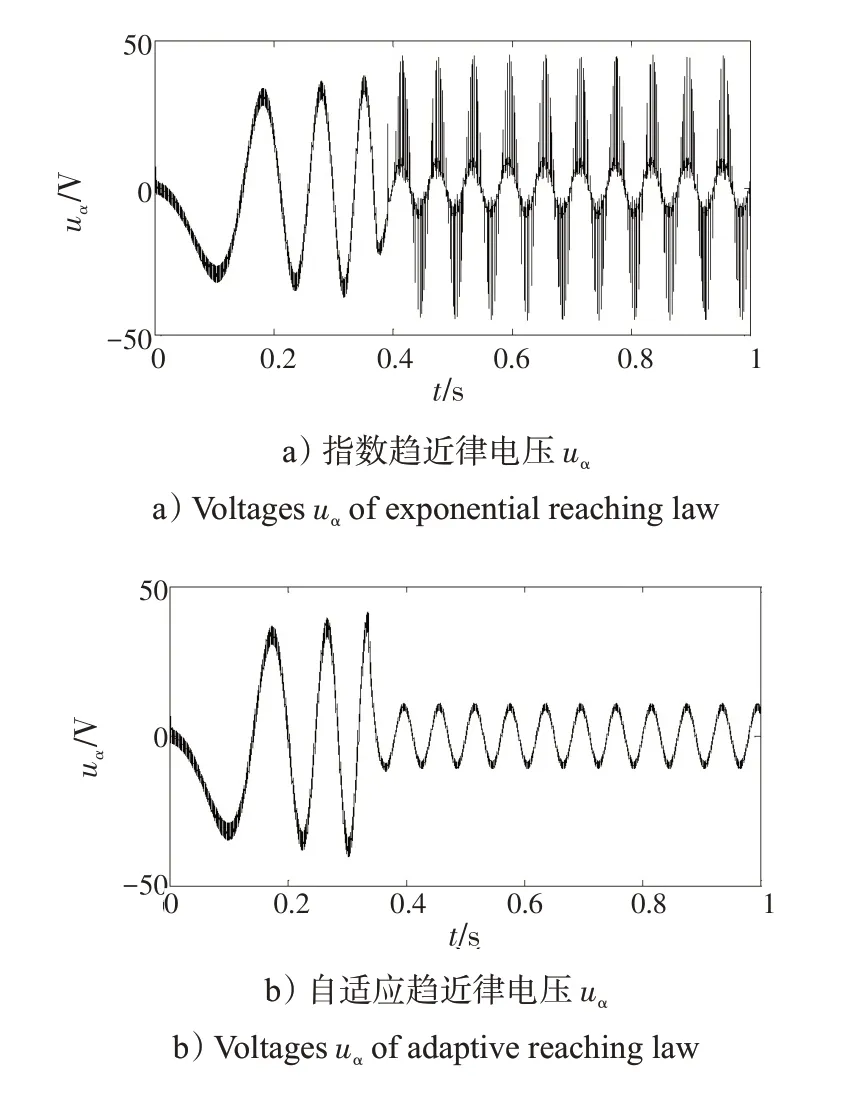
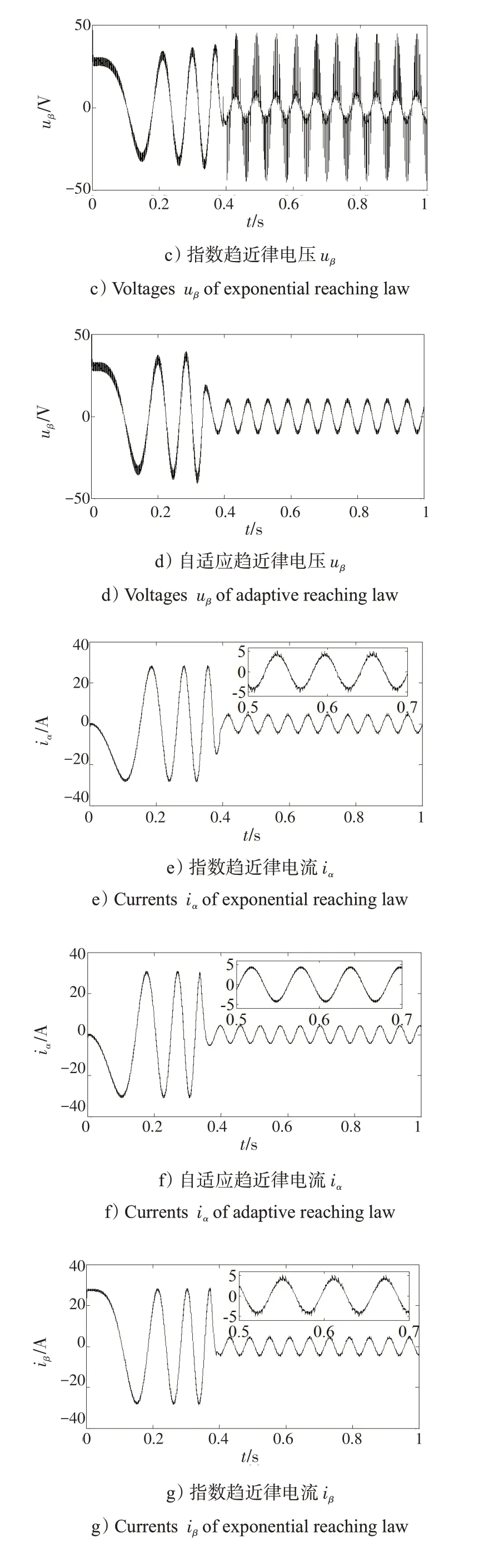
圖5 電機電壓uα、uβ 以及電流iα、iβ 波形比較Fig.5 Waveform comparison of motor voltages uα,uβ and currents iα,iβ

從圖4 可以看出，指數趨近律控制系統轉速動態調節時間較長，超調量較大，且到達穩態后轉速波動較大。電磁轉矩、電流iq超調量較大，且到達穩態后波動較大。A相電流穩態精度略顯不足。

自適應趨近律控制系統轉速動態調節時間短，超調量小，穩態性能良好。電磁轉矩、電流iq超調量較小，到達穩態時過渡光滑，波動較小。A相電流穩態性能良好。

從圖5 可以看出，指數趨近律控制系統電壓uα、uβ波動很大，導致電流iα、iβ穩態性能不足。而自適應趨近律控制系統電壓uα、uβ波動較小，電流iα、iβ穩態性能良好，這說明了電機具有良好的電磁轉矩和轉速。

3 結論

本文針對基于九開關變換器的對稱六相PMSM調速系統，提出了1 種基于自適應趨近律的滑模控制方法，建立對稱六相PMSM 調速系統數學模型，并將自適應趨近律控制方法應用于電機調速系統。仿真結果表明，相比于指數趨近律，自適應趨近律滑模控制方法能夠有效提高調速系統動態性能和穩態精度。