深部巖石爆破裂紋擴展與不耦合裝藥系數的關系

陳嘯林，張智宇，王 凱，彭 磊

（1.昆明理工大學國土資源工程學院, 云南 昆明 650093；2.昆明理工大學公共安全與應急管理學院, 云南 昆明 650093）

爆破過程中，介質最終的斷裂效果取決于裂紋的發展過程，裂紋控制是爆破控制的重要研究內容之一[1]。例如，在石油、頁巖氣開采等領域，需要采取有效的方法促進裂紋擴展。國內外相關學者開展了許多裂紋擴展研究，雖未取得重大突破，但仍有許多值得借鑒的成果。Bendezu 等[2]提出了一種基于有限元的數值方法，模擬了爆炸裂紋的傳播過程。楊仁樹等[3]通過室內模擬試驗，對高應力條件下炮孔穿透層中裂紋的起裂、擴展等動態力學性能進行了研究。田浩帆等[4]研究發現：在初始地應力條件下，巖石爆破過程中，裂紋擴展形成的壓碎區呈橢圓形，壓碎區的半徑隨地應力的增加而增大。岳中文等[5]采用一種新型激光動態焦散線試驗裝置，對單向圍壓下切縫藥包在爆破過程中爆生裂紋的力學性能進行了試驗研究。劉超等[6]利用RFPA2D-Dynamic 軟件，對不同地應力狀態下煤體中裂紋的擴展進行了研究，并對裂紋的發育、擴展及貫通情況進行數值模擬。不耦合系數指的是炮孔直徑與藥卷直徑之比，可通過改變藥卷直徑控制。徐穎等[7]分析了不耦合系數與爆破作用之間的關系，通過設計相應的試驗驗證了理論，研究結果表明，不耦合系數為1.67 時，裂紋擴展長度最長，且裂紋數與不耦合系數之間存在一種反比關系。程健[8]基于ANSYS 仿真模擬軟件，建立了煤體爆破的數值模型，并分析了不耦合系數等爆破參數，研究發現，爆破近區的破碎圈面積隨不耦合系數的減小而增大，裂紋數和密度也隨不耦合系數的減小而增大。霍曉鋒等[9]采用ANSYS/LS-DYNA 進行模擬，設計了單孔炸藥在不同不耦合系數下的破壞方案，結果表明，在不耦合系數為1.65 的情況下，炸藥破壞效率良好，保護區范圍較小，開掘區域有更多的爆裂產生，與此同時，在爆破中炸藥的能量利用率最高。對于含不同傾斜角度裂隙的介質，其裂紋的動態擴展問題十分復雜，沈世偉等[10]利用數字激光動焦散線模型試驗，在雙孔同步起爆的情況下，研究了預制不同傾斜角度裂隙的介質的爆生裂紋擴展規律。葛進進等[11]采用一種與硬巖力學特性相符的透明模型材料，進行了雙向荷載作用下的爆破試驗，研究了裂紋擴展方向與地應力的關系。

不耦合裝藥的形式被應用于許多場景[12]，不耦合系數在爆破控制中是一個關鍵參數。不耦合系數采用不合理，將會顯著影響巖石爆破效果及開采效率。數值仿真技術是一種重要的輔助研究方法，它與理論研究、試驗研究一樣，獲得了越來越多的重視，并在實際工程中得到了廣泛應用。隨著我國礦山開采深度的增加，地應力對爆破荷載的影響也逐漸增大，其作用不可忽視。然而，有些學者在研究過程中，僅考慮不耦合系數的影響，忽視了地應力的作用。本研究首先簡要回顧在數值模擬以及物理模型試驗中裂紋擴展研究的現狀和成果；其次，從數值模擬、相似試驗設計等方面研究深部巖石爆破過程中裂紋擴展與不耦合裝藥系數之間的關系；最后，基于現場獲取的相關參數，選用對應的本構方程，采用三維動力分析軟件LS-DYNA 研究初始地應力和不耦合系數對裂紋擴展的影響，以期為爆破工藝的優化和實際應用提供理論依據。

1 工程背景

以云南某礦山為例，頂部埋深800 m，礦床以花崗巖體為核心，呈東北分布。基于現場的勘察數據，對深部地區開展了成礦預測，確定了兩處重要礦業普查靶點。為此，通過研究深部巖石爆破裂紋擴展與不耦合裝藥系數之間的關系進行爆破參數設計，以達到良好的爆破效果，實現高效率的爆破開采。

2 數值模擬方法

以花崗巖為爆炸介質，開展地應力條件下不耦合裝藥系數對巖石爆破過程中裂紋擴展影響的數值模擬研究。

2.1 材料模型及參數

2.1.1 花崗巖

花崗巖的狀態方程采用線性狀態方程，本構模型采用Riedel-Hiermaier-Thomamodel（RHT）模型。

線性狀態方程的表達式為[13]

式中：p為爆壓，K為體積模量， ρ/ρ0為爆炸過程中介質當前密度與初始密度的比值。

RHT 模型考慮了應力張量的第三不變量對損傷面形狀的影響。如圖1(a)所示，其中，αvoid為孔隙度，當壓力低于孔隙壓碎壓力pcrush時，假設材料為彈性材料；之后，壓力不斷增加，當多孔材料被完全壓實時壓力為pcomp，該過程是塑性的。塑性變形過程中，對于給定的應力狀態和加載速率，只有當荷載超過其屈服極限時，材料才發生屈服。同時，該模型嵌入了與壓力相關的彈性極限面方程、失效面方程和殘余強度方程，如圖1(b)所示，其中，σ 為應力，D為損傷變量，εp為線性強化段累積等效塑性應變，具體表達式與參數見文獻[14–15]，破壞面、屈服面以及殘余面主要用于描述混凝土在沖擊荷載作用下的初始屈服強度、失效強度及殘余強度的變化規律。損傷變量的表達式為

圖1 RHT 模型Fig.1 RHT model

式中：εp為線性強化段累積等效塑性應變，為破壞時的等效塑性應變。

花崗巖的參數見表1、表2。表1 中：ρ 為密度，E為彈性模量，ν 為泊松比，σbc為巖石抗壓強度，Rm為巖石的抗拉強度，G為剪切模量。表2 中：fc為單軸抗壓強度，α0為初始孔隙度，pel為孔隙開始時的壓碎壓力，βc為壓縮應變率指數，βt為拉伸應變率指數，A1、A2、A3為Hugoniot 多項式參數，B0、B1、T1、T2為狀態方程參數， ε˙c0為參考壓縮應變率， ε˙t0為參考拉伸應變率， ε˙c為失效壓縮應變率， ε˙t為失效拉伸應變率，D1為初始損傷參數，D2為損傷參數，B為羅德角相關系數，g?t 為拉伸屈服面參數，為壓縮屈服面參數，A為失效面參數，n為失效面指數，fs?為剪壓強度比，ft?為拉壓強度比，Q0為拉壓子午比參數，ξ 為剪切模量縮減系數， εmp為最小失效應變，Af為殘余應力強度參數，nf為殘余應力強度指數，N為剩余的孔隙度指數。

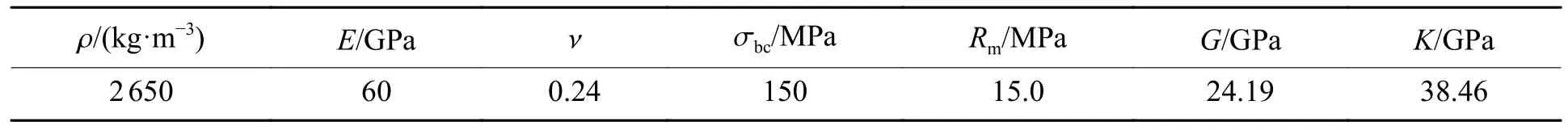
表1 花崗巖參數Table 1 Granite parameters

表2 巖石RHT 模型的部分參數Table 2 Some parameters of the rock RHT model

2.1.2 炸藥

用JWL 狀態方程描述炸藥，其表達式為[16]

式中：E0為爆炸產物的初始內能，J/m3；V為爆炸相對體積；Ae、Be、R1、R2、ω 均為常數，取值見表3。表3中，Cd為炸藥爆速。

表3 炸藥材料和JWL 狀態方程參數Table 3 Explosive materials and the JWL equation of state parameters

2.1.3 空氣

在不耦合裝藥數值模型中，藥卷四周有一層氣體，因此，在仿真模擬時，可以先使用其他關鍵詞替代藥卷周圍的氣體，如＊MAT_NULL，在建模結束后，將其參數改變為相應的氣體物料。藥卷周圍氣體采用LINEAR_POLYNOMIAL 狀態方程描述，表達式為

式中：Eair為空氣單位體積內能；μ為比體積，μ=1.4；C0～C6為方程系數，C0=C1=C2=C3=C6=0，C4=C5=0.4。

2.2 數值模型的建立

如圖2 所示，建立的模型尺寸為480 cm×400 cm×1 cm（長×寬×厚，分別對應x、y、z軸上的尺寸），兩炮孔沿中心水平軸線布置，并關于x=240 cm 對稱，孔距為80 cm，炮孔半徑為4 cm。利用LS-DYNA進行前處理建模，采用映射方法劃分模型。雙孔同時起爆，模型四周設為非反射邊界以模擬無限域巖石，求解時間設為1 000 μs。在耦合裝藥方式下，首先，在無地應力情況下觀察巖石雙孔爆破過程中裂紋擴展情況；其次，假設模型四周施加的圍壓荷載σx=σy，圍壓荷載隨著時間先線性增加后穩定至20 MPa（見圖3，加載末期，地應力的計算式見式(5)），觀察施加等圍壓荷載后地應力對巖石雙孔爆破過程中裂紋擴展的影響。此外，在施加等圍壓荷載的情況下，不耦合系數取1.2、1.4、1.6、1.8、2.0 進行裝藥，探究不耦合系數對巖石爆破過程中裂紋擴展情況的影響。

圖2 有限元模型示意圖Fig.2 Schematic diagram of finite element model

式中：σx、σy為水平應力，MPa；H為埋深，埋深約為800 m。

3 數值模擬分析

3.1 耦合裝藥方式下雙孔爆破過程中的裂紋擴展與壓力演化

3.1.1 無圍壓下巖石雙孔爆破過程中裂紋擴展與壓力的演化過程

圖4 給出了無圍壓下巖石雙孔爆破過程中裂紋擴展與壓力的演化過程。t=20 μs 時，受雙孔爆炸沖擊波作用，孔壁環向產生了范圍很小的壓碎區以及徑向微裂紋區。通過力學機制分析可知，壓碎區是由于徑向壓應力超過巖石的抗壓強度所造成的，而徑向微裂紋區是由于環向拉應力超過巖石的抗拉強度所致[17]。沖擊波向外傳播，當t=40 μs 時，巖石在拉伸應力的作用下形成徑向裂紋。隨后，徑向裂紋繼續擴展，兩壓力波相互接近，t=110 μs 時，兩壓力波相遇。當t=120 μs 時，應力波疊加處壓力增強。隨著時間的推移，應力波不斷向外傳播，可以觀察到應力疊加位置的上下移動，當t=180 μs 時，應力疊加位置見圖4 的紅色區域；當t=200 μs 時，兩孔壁周圍接近水平的徑向裂紋擴展到裂隙區，但并未相遇；t=230 μs 時，裂紋貫通兩孔；t=1 000 μs 時，裂紋擴展至整個幅面。

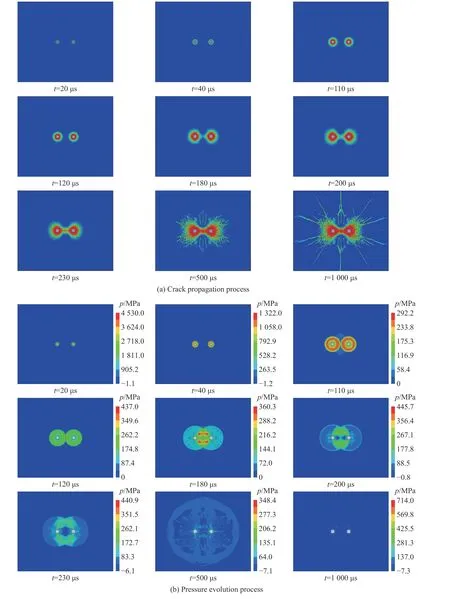
圖4 無圍壓下巖石雙孔爆破過程中裂紋擴展與壓力的演化過程Fig.4 Crack propagation and pressure evolution processes without confining pressure in rock under double-hole blasting

3.1.2 雙向等圍壓下巖石雙孔爆破裂紋擴展與壓力演化過程

圖5 給出了雙向圍壓均為20 MPa 時巖石雙孔爆破裂紋擴展與壓力的演化過程。

圖5 雙向等圍壓下巖石雙孔爆破裂紋擴展與壓力的演化過程Fig.5 Crack propagation and pressure evolution processes of rock under double-hole blasting with bidirectional constant confining pressure

比較圖4 和圖5 可以發現：地應力從零升至20 MPa 的過程中，粉碎區的形態基本保持不變，爆破粉碎區近似呈現圓形；加入地應力后，粉碎區的半徑有一定的增大趨勢；在粉碎區外側，裂紋以藥包為中心沿徑向分布，裂紋擴展演化規律在有無圍壓的情況下基本一致；相比于無圍壓的情況，施加雙向等圍壓后，在爆炸后期，徑向主裂紋的擴展長度明顯減小。

為了分析地應力對孔間環向應力的影響，圖6 給出了雙孔同時起爆條件下，無地應力和施加20 MPa 地應力時監測點A、B在爆破過程中的環向應力時程曲線。監測點A位于爆孔連線的中心，監測點B位于左側爆孔上方40 cm 處（見圖6 中的插圖）。對比圖6(a)、圖6(b)可知：無地應力條件下，A點的環向拉應力峰值和環向壓應力峰值分別為25.7 和165.0 MPa，B點的環向拉應力峰值和環向壓應力峰值分別為19.8 和137.0 MPa；當施加20 MPa 地應力時，A點的環向拉應力峰值和環向壓應力峰值分別為22.3 和281.0 MPa，B點的環向拉應力峰值和環向壓應力峰值分別為14.9 和234.0 MPa。以上結果表明，地應力的存在導致爆破環向拉應力減小，在施加地應力的方向上環向壓應力顯著增大，從而進一步抑制了裂紋的擴展[18–20]。因此，在有地應力條件下，初始地應力場的壓力效應對裂紋的產生和擴展起阻礙作用。

圖6 雙孔爆破過程中測點的環向應力時程曲線Fig.6 Hoop stress history curves of monitoring points under double-hole blasting

3.2 雙向等圍壓荷載下不耦合系數對巖石爆破裂紋擴展的影響

3.2.1 不耦合系數對孔壁應力峰值的影響

圖7 給出了不耦合系數k為1.0～2.0 的情況下孔壁應力pg時程曲線，其中，k=1.0 對應耦合裝藥，其余為不耦合裝藥。由圖7 可知：k=1.0 時，孔壁應力峰值達到最大，為2 280 MPa；k=1.2 時，孔壁應力峰值減小至1 270 MPa；k=1.4 時，孔壁應力峰值降低至621 MPa；隨著不耦合系數的進一步增大，孔壁應力峰值大幅度降低，當k為1.6、1.8、2.0 時，孔壁應力峰值分別為3 9 5、2 7 1 和191 MPa。因此，不耦合裝藥時的爆破損傷程度比耦合裝藥時的爆破損傷程度小，說明較大的不耦合系數不利于爆破破巖作業的開展[21]。

圖7 不同不耦合系數下孔壁的應力時程曲線Fig.7 Hole wall stress-time curves under different decoupling coefficients

3.2.2 不耦合系數對粉碎區、環向裂隙區半徑以及徑向裂紋擴展長度的影響

圖8 為不耦合系數k在1.2～2.0 區間時的裂紋擴展情況。由圖(8)可知，不同不耦合系數下，爆破后裂隙的發育過程類似，爆炸產生的沖擊波壓力會超過巖石的抗壓強度使其破碎，巖石形成最初裂縫，應力波以炮孔為中心向外傳播，爆生氣體在應力波的準靜態壓力作用下進入裂隙，在已有裂隙尖端形成很大的拉應力，裂紋進一步擴展[22]。k=1.2 時，強烈的爆炸沖擊波造成炮孔附近區域的巖石破碎，爆生氣體對裂紋具有明顯的驅裂作用，徑向裂紋延伸距離較遠。k=1.4 時，裂紋擴展的最大長度明顯減小。k=1.6 時，爆破損傷區域隨爆炸沖擊壓力的大幅降低而顯著減小，爆生氣體對裂紋的驅裂作用減弱，徑向裂紋擴展長度進一步縮減。k=1.8 時，僅在炮孔近區產生了極小范圍的巖層損傷，爆生氣體對裂紋擴展的影響較弱。k=2.0 時，爆炸沖擊壓力略大于巖石的單軸抗壓強度，僅引起炮孔近區花崗巖的起裂，裂紋擴展不明顯。

圖8 不同不耦合系數下裂紋的擴展情況Fig.8 Crack propagation under different decoupling coefficients

為定量分析不耦合系數對粉碎區半徑、環向裂隙區半徑以及徑向裂紋擴展長度的影響，利用軟件的測量功能對模擬結果進行測量，表4 列出了徑向裂紋擴展最大長度、粉碎區半徑以及沿著x、y、對角線方向（與x、y方向成45°夾角的方向）的環向裂隙區半徑。粉碎區屬于爆破近區，近似呈圓形，粉碎區沿x、y和對角線方向的尺寸基本相同，故只記錄一組數據。

將表4 的數據繪制成圖，得到雙向等圍壓下粉碎區半徑、環向裂隙區半徑以及徑向裂紋最大長度隨不耦合系數的變化規律，見圖9、圖10。可以看出，粉碎區半徑、最大環向裂隙區半徑、平均環向裂隙區半徑以及徑向裂紋擴展最大長度均隨不耦合系數增大而減小。原因如下：不耦合系數增大時，空氣介質對爆炸沖擊波的衰減作用增強，進而減弱應力波的作用，導致孔壁應力峰值降低，造成粉碎區半徑和環向裂隙區半徑逐漸減小；同時，此過程中爆生氣體引起的準靜態壓力效應得到增強，但是由于準靜態壓力效應往往滯后于應力波的作用，裂紋在高地應力條件下仍處于閉合狀態，在這種情況下，應力波所引起的徑向裂隙很難繼續擴展，因此，擴展裂紋的最大長度減小。

圖9 雙向等圍壓下粉碎區半徑和裂隙區半徑隨不耦合系數的變化規律Fig.9 Variation laws of radii of crushing zone and fracture zone with decoupling coefficient under bidirectional constant confining pressure

圖10 雙向等圍壓下徑向裂紋最大長度隨不耦合系數的變化規律Fig.10 Variation law of the maximum length of radial crack with decoupling coefficient under bidirectional constant confining pressure

4 動焦散相似試驗

Murphy 等[23]將均質巖石與有機玻璃（polymethyl methacrylate，PMMA）進行了等效爆破，二者在爆破荷載作用下的破壞形式基本一致。PMMA 具有良好的光學透明度，通過動焦散試驗可以準確地獲得PMMA 裂紋擴展形態。本研究通過數值模擬獲得了雙向等圍壓荷載下不耦合系數與巖石裂紋擴展特性的關系，為驗證研究結果的正確性，開展了PMMA 動焦散相似試驗。PMMA 的動態力學參數列于表5,其中：σm為有機玻璃的抗壓強度，Cp為縱波波速，Cs為橫波波速。

表5 有機玻璃的動態力學參數Table 5 Dynamic mechanical parameters of PMMA

4.1 模型試驗的相似性和相似系數

根據相似準則，模型的相似性可歸納為模型的材料相似、幾何相似和爆破動力相似[24]。因此，從這3 個方面分析此次試驗的相似性和相似系數。

4.1.1 材料相似

模型材料相似系數η 為

本研究中花崗巖的抗壓強度為150 MPa，有機玻璃的抗壓強度為130 MPa，因此，模型的材料相似系數η 為0.87。

4.1.2 幾何相似

依據原型和模型的平衡、幾何、物理方程等，各物理量之間的相似關系如下[25]

式中：α 為相似比，下標L、δ、E、ν、γ、σ 代表長度、位移、彈性模量、泊松比、容重、應力，σc為抗壓強度，σt為抗拉強度，ε 為應變，下標X、Y、Z代表體積力，C為內聚力， φ為內摩擦角，T為時間。

在盡量減小模型試驗失真程度和尺寸效應對試驗結果影響的前提下，將模型試件尺寸定為300 mm×300 mm×10 mm，得到幾何相似系數αL=16。

有機玻璃的容重γ 為11.8 kN/m3。基于容重相似關系得到容重相似比αγ=2.24，并進一步求得應力相似系數ασ=35.8。

4.1.3 爆破動力相似

試驗選用二硝基重氮酚（diazodinitrophenol，DDNP）炸藥，其密度約為1 200 kg/m3，爆速可達4.0 km/s。礦山爆破通常選用乳化炸藥，其密度為1 150 kg/m3，爆速為4.5 km/s。模型試驗與實際爆破所使用的炸藥類型不同，“炸藥爆炸能量相似”原則[26]要求模型炸藥與原型炸藥間應滿足CρCD=1（Cρ為原型炸藥與模型炸藥的密度比，CD為原型炸藥與模型炸藥的爆速比)。根據本研究中的原型炸藥和模型炸藥參數，可得CρCD=1.08，基本符合“炸藥爆破能量相似”原則。

4.2 試驗設計

采用有機玻璃板作為模型材料，根據應力相似系數ασ=35.8 以及式(5)，求得所施加的圍壓荷載為0.6 MPa。試驗在雙向等圍壓情況下開展，試件材料中心預制一個炮孔，炮孔直徑為10 mm，藥卷直徑可變，分別為8、7、6 和5 mm，相應的不耦合系數k分別為1.2、1.4、1.7 和2.0。為了減小試驗誤差，各個試件的其他參數保持一致。

4.3 試件爆后形態分析

圖11 為雙向等圍壓荷載下試件爆后的形態。圖11(a)、圖11(b)顯示，隨著不耦合系數的增大，徑向裂紋的擴展范圍逐漸減小，圖11(c)、圖11(d)顯示試件僅有少數徑向裂紋出現。由此可得，高地應力條件下，較小的不耦合系數有利于裂紋的擴展。

圖11 試件爆后的形態Fig.11 Specimen patterns after explosion

為分析徑向裂紋擴展長度與不耦合系數之間的關系，對爆后模型試件表面裂紋的擴展形態進行了復刻，如圖12 所示。通過對爆后試件進行測量，獲得了徑向裂紋擴展長度、粉碎區半徑和沿著x、y方向以及對角線方向的裂隙區半徑，結果列于表6 中。粉碎區屬于爆破近區，近似呈圓形，x、y方向以及對角線方向的尺寸基本相同，故只記錄一組粉碎區半徑數據。

圖12 爆后試件裂紋擴展形態Fig.12 Crack propagation morphology of specimen after explosion

從表6 可知，粉碎區半徑、最大環向裂隙區半徑、平均環向裂隙區半徑以及徑向裂紋擴展最大長度均隨不耦合系數增大而減小，與數值模擬結果一致，進一步證實了數值模擬結果的準確性。

裂紋擴展長度是反映巖石介質爆破效果的一個重要參數，根據表6 中模型試件的測量結果，得到了徑向裂紋長度最大值及平均值隨不耦合系數的演變規律，如圖13 所示。

圖13 雙向等圍壓下試件徑向裂紋長度隨不耦合系數的變化規律Fig.13 Variation law of radial crack length of specimen with decoupling coefficient under bidirectional constant confining pressure

由表6 可知，模型試驗中，k為1.2、1.4、1.7 和2.0 時的徑向裂紋擴展最大長度分別為9.4、7.9、5.3 和3.5 cm。為了提高模型的預測精度，將徑向裂紋擴展長度最大值lr,max與不同不耦合系數k采用冪函數擬合，擬合式為

該擬合曲線的擬合精度R2達到0.974。從式(8)能夠看出，裂紋長度隨1/k的增加而增大。式(8)對于爆破參數設計、實現爆破高效率開采具有較高的參考價值。

5 結 論

通過數值模擬研究了深部巖石爆破過程中裂紋擴展與不耦合裝藥系數的關系，并通過動焦散相似試驗驗證了關系的正確性，得到的主要結論如下。

(1) 深部巖體的巖石爆破過程中裂紋的擴展行為與地應力存在明顯的對應關系。有地應力條件下的徑向主裂紋擴展長度明顯小于無地應力條件下，因為在施加地應力的方向上環向拉應力降低，同時，壓應力效應增強，抑制了裂紋的擴展。由此可得，在地應力條件下，初始地應力場產生的壓力效應對爆破裂紋的產生和擴展起阻礙作用。

(2) 雙向等圍壓荷載下不耦合系數k為1.2～2.0 時巖石爆破過程中裂紋擴展的數值模擬結果表明：隨著不耦合系數的增大，粉碎區半徑、裂隙區半徑、徑向裂紋擴展的最大長度以及炮孔孔壁應力峰值均逐漸減小。

(3) 通過動焦散試驗建立的不耦合系數（大于或等于1.2 時）與徑向裂紋擴展長度間的關系式為lr,max=14.5(1/k)1.56，擬合精度達0.974，擬合效果較好，對于爆破參數設計具有較高的參考價值，對礦山深部開采背景下爆破開采效率的提升具有一定的指導作用。