2024鋁合金切削過程微觀力學強化機理研究

宋 徽 張國智

（1.建筑學院，新鄉職業技術學院，新鄉 453000；2.機電工程學院，新鄉學院，新鄉 453000）

1 引言

切削過程是機械制造中最為常見的過程，長期以來人們試圖在實際加工之前對這一過程進行計算機模擬和理論模型的建立[1]，以及相關刀具性能模擬[2]，提出了很多理論模型，最早提出了剪切角的理論切削模型，此外，國內外學者還提出了很多的切削過程的模擬模型，但還沒有一個準確的模擬模型。但切削過程中切削力的計算已較為成熟，提出了很多切削力的理論和經驗的計算模型[3，4]，并且與實際實驗結果吻合較好。但切削過程是較為復雜的過程，也是一個高度非線性熱結構場耦合分析[5]，因而，要想準確地對這一過程進行計算機模擬，需要在機理上研究材料在切削加工過程的力學性能的變化。在模擬切削過程中，最難解決的是兩個問題：一是切屑形成與斷裂準則；二是加工完成后工件表層力學性能的變化。但這對于預測工件加工變形及殘余應力至關重要。此外，對于機械表面失效分析也很關鍵[6]。2024鋁合金廣泛應用于航空航天、建筑裝潢中，目前，關于此材料切削強化的機理性研究還不是很深入系統。本文以有限元數值計算為仿真手段，在對切削過程進行模擬的基礎上，從微觀塑性力學的角度揭示切削過程中表層材料力學性能的變化機理。

2 基于仿真技術的切削過程機理分析方案

基于有限元仿真手段，首先建立切削過程的耦合場分析的有限元模型，在對切削過程的應力場及溫度場分析結果的基礎上，對局部切削點的組織結構在切削過程中的變化進行分析，然后，在有限元仿真分析的基礎上，基于微觀塑性力學理論，對材料在切削過程中的力學性能變化進行機理上的分析與研究。具體的分析流程如圖1所示。

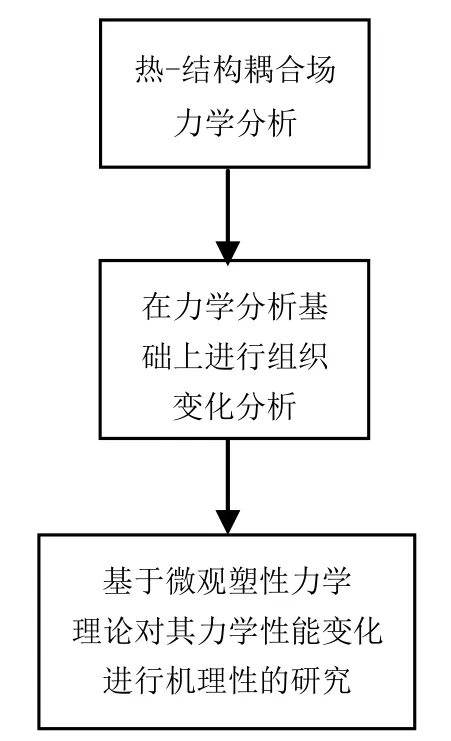
圖1 切削過程力學機理仿真分析流程

3 切削過程的有限元分析

3.1 應力及溫度分析

建立了切削過程的熱結構場耦合分析的有限元模型，有限元模型圖如圖2所示，材料選用的是2024鋁合金，初始加工溫度為20℃，選用的刀具為TNMA332，刀具參數示意圖如圖3所示，各參數分別為：IC=9.53，T=4.76mm，R=0.8mm，B=13.494mm，H=3.81mm。切削時，切削參數為：切削速度為250mm/s，進給速度為0.35mm/r，切削深度為 0.3mm。熱傳導系數為45N·s-1·mm-1·℃-1，切削長度為3.5mm，剪切摩擦系數取為0.5，計算的迭代步數為10000，在計算的過程中，使用網格重劃分技術。

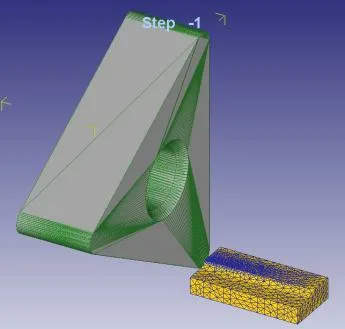
圖2 切削過程的有限元模型圖

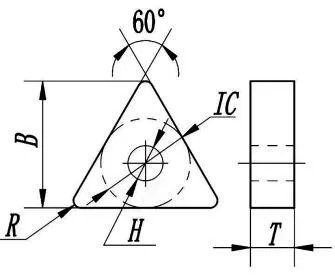
圖3 刀具參數示意簡圖

切削過程完成時的結構場的有限元分析結果如圖4所示，從圖4a 中可見，在局部切削處的等效應力很大，應力分布極不均勻，從圖4b 中可見，切削區域處的某點在切削過程中隨著切削的進行應力逐漸增大。

切削過程完成時的溫度場的有限元分析結果如圖5所示，從圖5a 中可見，在局部切削處的溫度有很大的升高，在局部最高溫度為327℃，溫度場分布極不均勻，圖4b 中的節點在切削過程中的溫度變化如圖5b所示，從圖5b 中可見，該點在切削過程中隨著切削的進行溫度逐漸升高，主要是由摩擦熱及塑性功轉化成熱能造成的。

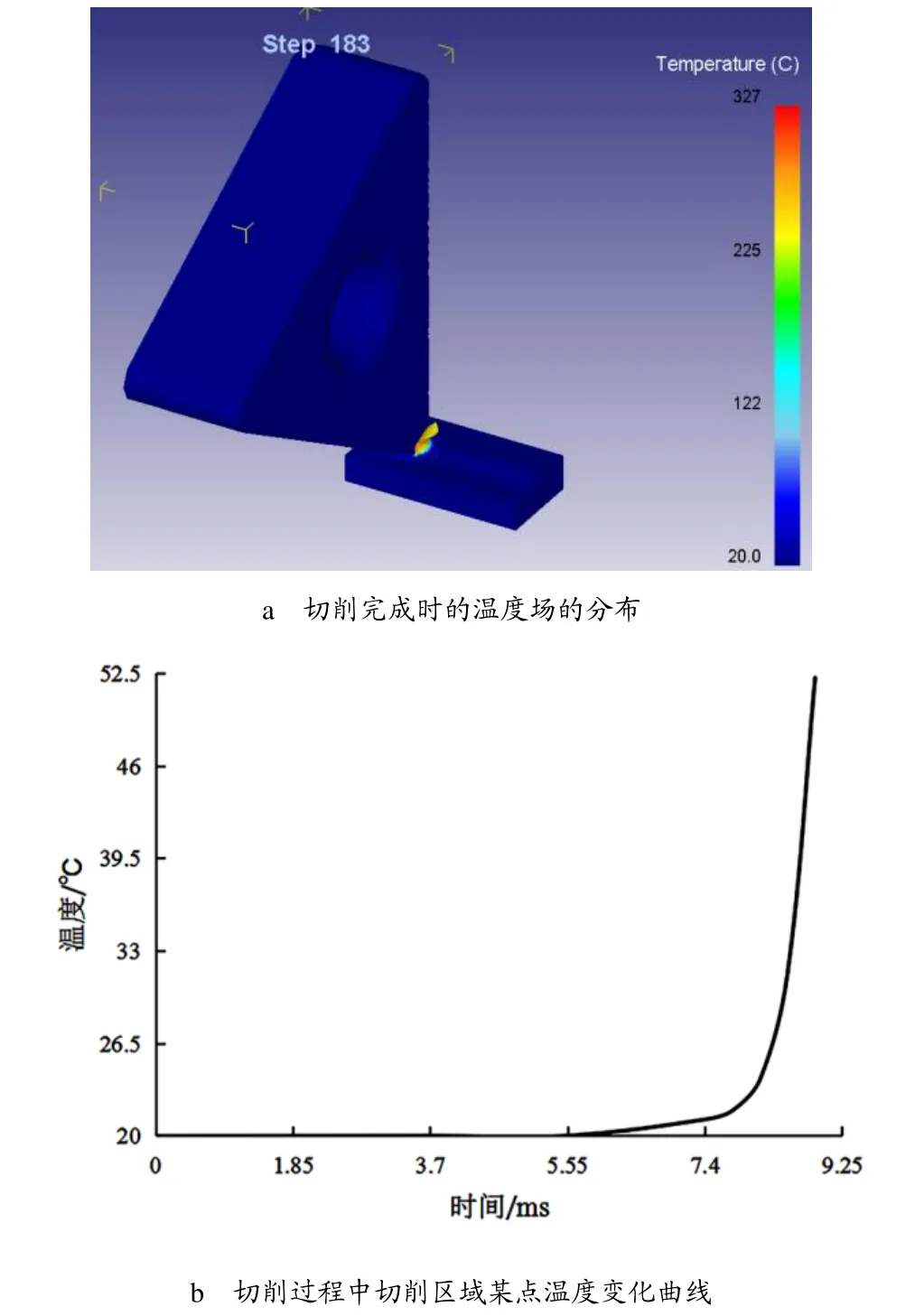
圖5 切削過程的溫度場的有限元分析結果

3.2 組織變化分析

在切削過程的熱結構耦合場分析結果的基礎上，對切削過程中組織結構的微觀變化進行了進一步計算，得出切削過程中切削區域中局部塑性變形后，在組織結構上的具體變化，如晶粒尺寸、晶界、位錯密度等。在計算過程中，選取了切削完成時刻的切削根部點作為微組織結構計算區域，并對遠離切削區域的點進行計算。如圖6所示，在計算過程中，選取的計算區域為3mm×5mm，放大因子為2。對比圖6a 和圖6b 可知，在切削過程中，切削區域組織結構發生了較大變化，晶粒尺寸和位錯密度顯著增加，所以，在切削區域發生了加工硬化現象，而遠離區域變化較小。

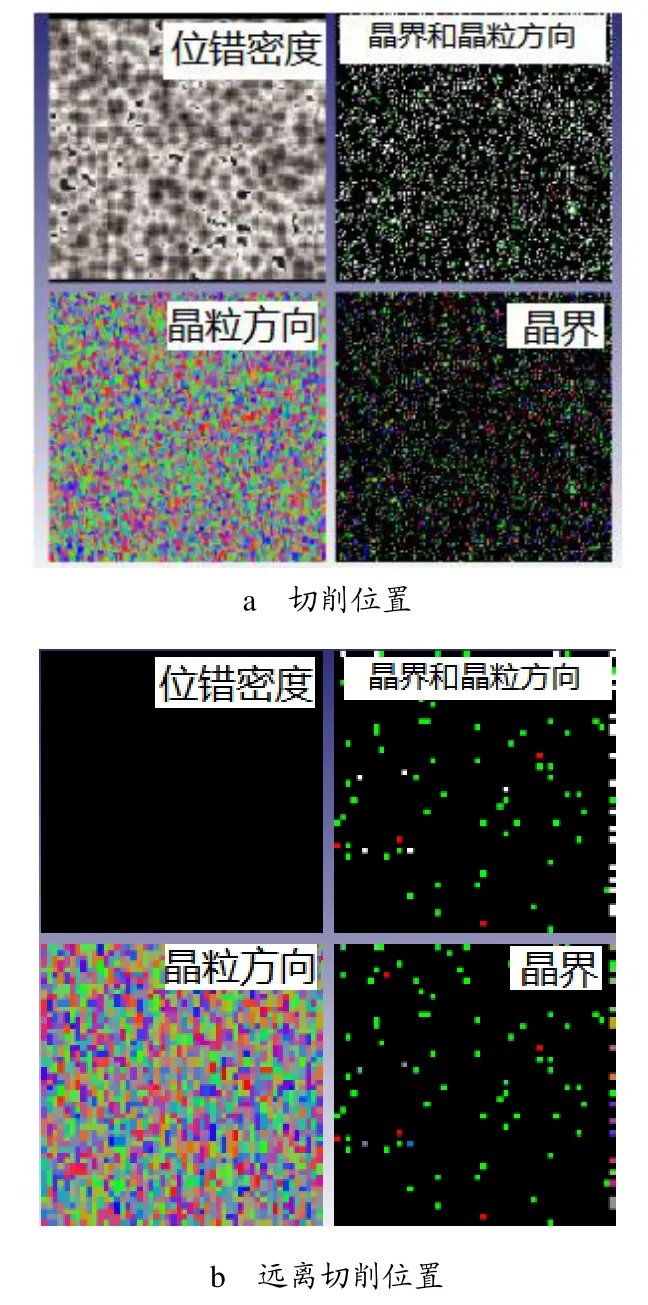
圖6 組織變化計算結果

3.3 力學機理分析

切削過程中組織結構的變化造成了對其切削表層材料力學性能主要參數的影響，如彈性模量、泊松比、屈服應力、剛性模量等。切削表層材料的力學性能變化不僅對表面的各種力學性能產生了較大影響，而且對于其工件表面的加工變形及其中的殘余應力產生了較大影響。對其工件的表面變形及其內部殘余應力的計算準確，需分析其在切削過程中表層材料力學性能的變化。

基于微觀塑性力學理論可知，彈性模量、泊松比在切削過程中受晶粒結構的變化影響較小，可近似認為不發生變化，而材料的塑性指標如屈服應力發生了較大的變化，但剛性模量，即雙線性硬化材料模型的第二條曲線的斜率幾乎不發生變化。

根據微觀塑性力學中的MSG（mechanism-based strain gradient）理論和Hall-prtch 準則，切削加工后表層材料的屈服應力可由式（1）計算：

其中，σs為材料的初始屈服應力（表層材料切削完成后的屈服應力）；G為剪切模量；b為Burgers矢量；α0為Taylor系數，其值約為0.3；ρ為位錯密度，產生于材料中的非均勻塑性變形；M為Taylor因子，對面心立方多晶體（fcc）金屬材料，M=3.06；k為Hall-prtch參數；d為平均晶粒尺寸[7]。

根據文中組織分析的有限元計算結果、相關實驗、文獻，σs=250MPa，G=27GPa，b=0.281nm，α0=0.3，M=3.06，ρ=1.4×1013m-2，k=4.8MPa/μm0.5，d=18μm，根據式（1），計算得出2024鋁合金表層材料在切削完成時的屈服應力增加了46.42MPa。拉伸實驗圖如圖7所示，圖7b為工程應變與工程應力的拉伸曲線，由圖7b可見，切削后的試件未做去除應力處理與去除應力處理后相比，強度略有提升，屈服應力處的增加值與文中計算的增加值的誤差僅為6.75%，與文中分析結果相符。當然，表層材料在切削完成時的屈服應力增加值與各種加工參數相關，如切削速度、進給量、切削深度等。由此可知，材料經過切削加工后表層材料的塑性力學性能參數發生了較為明顯的變化。

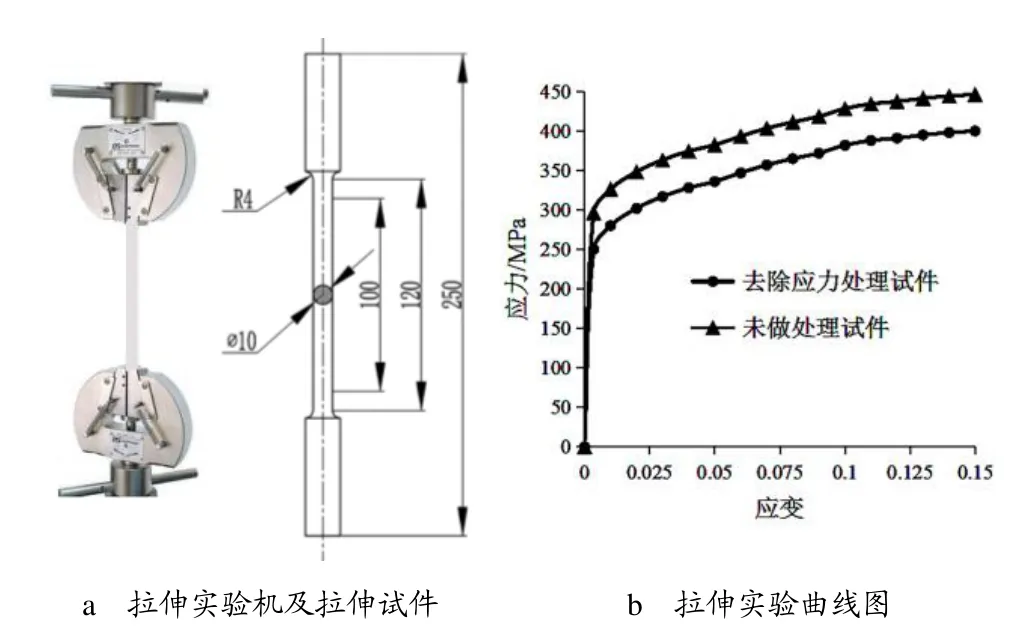
圖7 拉伸實驗圖

鋁合金布氏硬度和抗拉強度轉換關系如下：

2024鋁合金未切削試件的表面硬度實驗檢測其硬度值的布氏硬度為117，代入式（2）中得其抗拉強度為403.65MPa，切削試件的表面硬度實驗檢測其硬度值的布氏硬度為131，代入式（2）中得其抗拉強度為451.95MPa，增加了48.3MPa，與根據式（1）計算的抗拉強度增加值的理論計算值的誤差為3.89%，這個誤差比拉伸實驗的誤差小，表明表面硬度實驗更能直接反映切削后2024鋁合金的表層抗拉強度略有增加，進一步驗證了本文的仿真和理論分析的準確性。

綜上所述，經過切削加工后，實際加工表面的材料力學性能由于組織結構的變化而發生了很大變化，尤其其塑性性能指標，如屈服應力，主要是晶粒尺寸與位錯密度造成的，因而，對加工后的零件進行精確分析計算及對表面加工變形或殘余應力計算時，必須考慮晶粒尺寸與位錯密度等組織結構的變化造成的表層材料塑性性能變化，并在此基礎上建立動態的本構模型，從而對零件的工作性能及表面的摩擦磨損性能進行更精確地分析計算。

4 結束語

本文針對切削過程中表層材料力學性能的變化進行研究，首先，結合微觀塑性理論，提出了基于有限元仿真的分析方案，建立了切削過程的熱結構場耦合分析的有限元模型，并對典型參數的切削過程進行了有限元模擬，在切削局部最高溫度為327℃；其次，在此基礎上進行了切削過程中微觀組織的計算，得到了切削區域及遠離切削區域處的晶粒方向、位錯密度、晶界分布，可知，切削區域組織結構發生了較大變化，晶粒位錯密度顯著增加，其數值為1.4×1013m-2；最后，基于MSG 理論和Hall-prtch 準則，通過計算，2024鋁合金表層材料在切削完成時的屈服應力增加了46.42MPa，這與實際測試結果相符，誤差僅為6.75%，抗拉強度增加值與表面硬度實驗的檢測值誤差為3.89%。本文的研究對切削過程的精確模擬、表面加工變形的精確計算、表面摩擦磨損性能的精確分析具有工程應用和理論研究價值。