改進的Ramp孿生支持向量機聚類

陳素根，劉玉菲

1.安慶師范大學 數理學院，安徽 安慶 246133

2.安徽省大別山區域復雜生態系統建模、仿真與控制重點實驗室，安徽 安慶 246133

3.安徽省皖江流域種群生態模擬與控制國際聯合研究中心，安徽 安慶 246133

聚類分析是無監督學習問題，它考慮無標簽數據內部自身結構，將數據聚成若干類，被廣泛應用于社區檢測、圖像處理和基因分析等方面[1-2]。K-means 算法[3]是經典的基于劃分思想的聚類算法，它通過迭代尋找k個聚類中心點，使得總體誤差最小。受K-means算法的啟發，通過迭代尋找k個聚類中心平面。2000年，Bradley 等人[4]提出了k平面聚類算法（K-plane clustering，KPC），開啟了基于平面聚類算法的新思路。然而，KPC通過二次函數度量類內散度，要求數據點盡可能接近聚類中心平面，僅僅考慮了類內的數據點對聚類效果影響，從而該算法聚類效果不佳。為了克服KPC存在的問題，Liu等人[5]提出了k近端平面聚類算法（K-proximal plane clustering，KPPC），KPPC同時考慮了類內數據點和類間數據點的影響，每類數據點更加接近該類中心平面而其他類數據點盡可能遠離。為了提升KPC 和KPPC 的性能，2015年，Wang 等人[6]提出了孿生支持向量機聚類算法（twin support vector clustering，TWSVC），該算法需要求解一系列二次規劃問題，計算相對復雜。同時，TWSVC 基于Hinge 損失函數度量類間離散程度，由于Hinge 損失函數是無界函數，導致TWSVC 算法對遠離中心平面的數據點比較敏感。為了解決這個問題，2019 年，Wang 等人[7]利用有界的Ramp 損失函數代替Hinge 損失函數，提出了基于Ramp 損失的孿生支持向量機聚類算法（Ramp-based twin support vector clustering，RampTWSVC），該算法通過交替迭代求解非凸優化問題，對遠離聚類中心平面的數據點相對魯棒。然而，Ramp 損失函數是一種對稱的函數，對聚類中心平面兩邊的數據點采用相同的懲罰，沒有考慮數據分布的問題[8]。近年來，支持向量機損失函數方面的研究被廣泛關注[9-11]，且非對稱損失函數的孿生支持向量機聚類算法逐漸成為新的研究熱點[12-13]。

綜上分析，受RampTWSVC 和非對稱損失函數的啟發，本文首先構造了一個非對稱Ramp 損失函數，并在此基礎上提出了改進的Ramp損失孿生支持向量機聚類算法，簡稱IRampTWSVC。該算法有以下優點：（1）非對稱Ramp損失函數繼承了Ramp損失函數的有界性特點，可以有效降低遠離聚類中心平面數據點對聚類中心平面的影響。同時，它又具有非對稱損失函數的優點，對不同位置的數據點采用不同的懲罰，使得該算法更加魯棒。（2）參數t可以靈活調節非對稱的Ramp損失函數的表達式，以適應不同的數據分布，使得IRampTWSVC 具有更好的泛化性能。特別地，當參數t等于1 時，IRampTWSVC 退化為RampTWSVC。（3）多個UCI數據集和人工數據集上的實驗結果表明本文所提IRampTWSVC算法的有效性。

1 相關工作

對于聚類問題，本文考慮m個n維數據點{x1,x2,…,xm}，用一個矩陣表示為X=(x1,x2,…,xm)∈Rn×m，第i簇數據點構成一個矩陣Xi，其余簇的數據點構成一個矩陣。設這m個數據點屬于k簇，對應的標簽為y∈{1,2,…,k}。

對于含有k簇的聚類問題，TWSVC 尋找k個聚類中心平面，設第i簇中心平面為：

它要求第i簇數據點盡可能聚集在這一簇中心平面周圍，其余簇數據點盡可能遠離這一簇中心平面。線性TWSVC優化問題[6]如下：

其中，c表示懲罰參數，ξi是松弛向量，e表示分量全為1的適當維數向量。

經過一系列推導，優化問題（2）轉化為如下對偶問題：

受TWSVC 啟發，Wang 等人[7]利用有界的Ramp損失函數代替Hinge 損失函數，提出了基于Ramp 損失的孿生支持向量機聚類算法（RampTWSVC）。Ramp損失函數定義如下：

其中，Δ∈[0,1)和s∈(-1,0]是用于控制損失函數形式的兩個常量，|ρ|=x+bi|表示偏差，(ρ)表示類內損失函數，(ρ)表示類間損失函數。

對第i簇中心平面，線性RampTWSVC的優化問題為：

其中，f(xj;wi,bi)=+bi。

簡單起見，記ui=(wi,bi)T，將每個數據點維數增加一維且取值為1。于是，第i簇數據點記為Zi=[Xi,e]，其余簇的數據點記為=[,e]。經過一系列代數運算，式（5）可轉化為：

顯然，式（6）是一個非凸優化問題，引入輔助向量p1∈{-1,0,1}mi和p2∈{-1,0,1}m-mi，其中mi表示第i簇數據點個數，優化問題式（6）等價于下面的混合整數規劃問題：

其中，p1(j)和p2(j)分別表示p1和p2的第j個元素。

給定初始向量，通過式（7）的約束條件計算(t=1,2,…)固定時，式（7）轉化為一個無約束凸優化問題，可以通過序列最小優化（sequential minimal optimization，SMO）等算法求解。當解出之后，再通過式（7）更新和，這樣不斷交替迭代下去，直到式（7）的目標函數值不下降，終止迭代并得到最優解。對任意數據點x，按照以下規則進行聚類：

利用核技巧可將線性RampTWSVC模型推廣到非線性RampTWSVC模型，詳細內容可見參考文獻[7]。

2 IRampTWSVC

2.1 非對稱Ramp損失函數

由Ramp損失函數的定義知道，它是一種對稱的損失函數，對聚類中心平面兩側的數據點采用相同懲罰，沒有考慮數據的分布。因此，本文對Ramp 損失函數進行改進，構造一種非對稱的Ramp 損失函數，對不同位置的數據點采用不同的懲罰，具體定義如下：

其中，Δ∈[0,1)，s∈(-1,0]和t∈[0,1]是用于控制損失函數形式的3個常量，(ρ)表示類內損失函數，表示類間損失函數，|ρ|=+bi|表示偏差。

顯然，由式（9）可知，非對稱Ramp損失函數也是有界函數，保留了Ramp 損失函數有界的特性，繼承了Ramp損失函數的優勢，可以有效降低遠離聚類中心平面的數據點對聚類中心平面的影響，從而對噪聲或異常點具有較好的魯棒性。特別地，當t=1 時，非對稱Ramp 損失函數退化為Ramp 損失函數。同時，當參數t在[0,1)之間取值時，式（9）所定義的損失函數為非對稱的，它對聚類中心平面兩邊的數據點采用不同的懲罰，有利于刻畫數據的分布特征，使模型具有更好的泛化性能。

總之，式（9）所定義的非對稱Ramp 損失函數是基于數據分布的，從類內損失和類間損失兩個角度考慮給予數據點不同的懲罰。對于類內損失函數，損失函數值隨數據點到第i簇聚類中心平面的距離線性增長，距離聚類中心平面越遠，損失函數值越大，定義為ρ(xj)的一次函數。但是，當數據點到第i簇聚類中心平面的距離小于1-Δ或大于2-Δ-s時，損失函數值分別賦予常數。對于類間損失函數，距離第i簇聚類中心平面越遠，損失函數值越小，也定義為ρ(xj)的一次函數，當數據點到第i簇聚類中心平面的距離小于-s或大于1+Δ時，損失函數值分別賦予常數。同時，對于類內損失函數和類間損失函數有一個原則，也就是類內數據點的損失值不會大于類間數據點的損失值，且都保持有界性特征。

圖1分別給出了當Δ=0.3，s=-0.2，t=0,0.2 和0.4 的非對稱Ramp 損失函數的示意圖，其中圖1（a）為類內損失函數，圖1（b）為類間損失函數。從圖1可以看出，參數t對損失函數有較大的調節作用，使得損失函數表達式更加豐富，以適應不同的數據分布。參數t控制著損失函數值變化的快慢和損失函數值的上下界，保證類內損失函數值不超過類間損失函數值。

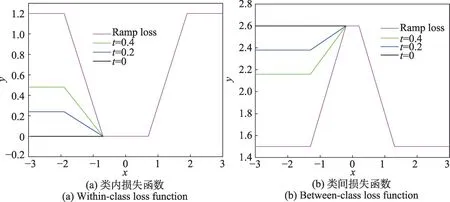
圖1 非對稱Ramp損失函數的示意圖Fig.1 Illustration of asymmetric Ramp loss function

2.2 線性IRampTWSVC

基于非對稱Ramp 損失函數，本文提出改進的RampTWSVC，記為IRampTWSVC。類似于Ramp-TWSVC，對于第i簇聚類中心平面，線性IRampTWSVC的優化問題為：

在目標函數式（10）中：第一項表示正則項，控制模型的復雜性；第二項表示類內損失，最小化這一項使得第i簇中的數據點到第i簇聚類中心平面的距離|ρi(xj)|盡可能小，從而這些數據點盡可能聚集在該類的聚類中心平面周圍；第三項表示類間損失，最小化這一項使得其余簇的數據點到第i簇聚類中心平面的距離|ρi(xj)|盡可能大，從而這些數據點盡可能遠離第i簇聚類中心平面。根據非對稱的Ramp損失函數的定義式（9）可知，類內損失函數和類間損失函數都是有界的分段函數，它們根據數據點的位置給予不同的懲罰，使得遠離聚類中心平面的數據點不會對聚類中心平面產生更大的影響，從而增強了模型的魯棒性。

簡單起見，記ui=(wi,bi)T，將每個數據點維數增加一維且取值為1。于是，第i簇數據點記為Zi=[Xi,e]，其余簇的數據點記為=[,e]。類似于RampTWSVC的推導過程，經過一系列代數運算，式（10）可轉化為：

其中，p1(j)和p2(j)分別對應的是p1和p2的第j個元素。

給定初始向量u(0)i，通過式（11）的約束條件計算(t=1,2,…)固定時，式（11）轉化為一個無約束凸優化問題，將其轉化為對偶問題：

Xi表示第i簇數據點，表示不屬于第i簇的數據點。

顯然，式（12）為有約束的二次規劃問題，可以通過SMO算法求解出。當解出之后，再通過式（11）更新和，這樣不斷交替迭代下去，直到式（11）的目標函數值不下降，終止迭代并得到最優解。對任意數據點x，再按照以下規則聚類：

綜上所述，給出線性IRampTWSVC 算法步驟如下：

算法1線性IRampTWSVC

實際上，算法1 是一個交替迭代優化算法，其求解過程與RampTWSVC類似，終止于有限步迭代，獲得模型的局部最優解，相關理論證明可參考文獻[7]。

2.3 非線性IRampTWSVC

對于非線性情形，首先選擇合適的核函數K將數據映射到高維特征空間中，然后利用核技巧推廣到非線性IRampTWSVC 模型。與線性情況類似，非線性IRampTWSVC優化問題如下：

其中，ρi(K(xj,X))=K(xj,X)Twi+bi且cw,cb>0 是參數。

類似地，記ui=(wi,bi)T，將每個數據點增加一維且取值為1。第i簇的數據點記為Ki=[K(Xi,X),e]，其余簇的數據點記為=[K(,X),e]。非線性IRamp-TWSVC模型的求解過程與線性IRampTWSVC 模型的算法步驟非常相似，唯一不同的是先選擇合適的核函數K將數據映射到高維空間，此處不再贅述。

3 實驗結果與分析

為了驗證本文所提IRampTWSVC 算法的性能，選取8 個UCI 數據集Iris、Haberman、Zoo、Wine、Glass、Blood、Seeds 和Lenses（https://archive.ics.uci.edu/ml/datasets.php）以及5 個人工數據集Flame、Compound、Simplex、Spherical_4_3 和Spherical_5_2（https://github.com/deric/clustering-benchmark/tree/master/src/main/resources/datasets/artificial）進行實驗。具體實驗環境：MATLAB R2019b，硬件配置為Windows 11操作系統，16 GB內存，2.10 GHz主頻CPU的計算機。選取KPC[4]、KPPC[5]、TWSVC[6]和RampTWSVC[7]作為實驗對比算法，與IRampTWSVC 進行實驗比較。實驗中均采用網格尋優的方法為各算法選擇最優參數，KPC、KPPC、TWSVC和RampTWSVC中的參數c、cw、cb范圍為{2i|i=-5,-4,…,5}，IRampTWSVC中的參數t的范圍設置為{0,0.1,0.2,…,1}。對于非線性情形，選擇高斯核函數K(x,y)=e-||x-y||2/2μ2，核參數μ的范圍為{2i|i=-5,-3,-1,…,5}。根據經驗，Ramp-TWSVC 和IRampTWSVC 中的參數Δ和s分別設置為Δ=0.3 和s=-0.2，所有算法均采用近鄰圖（nearest neighbor graph，NNG）[14]初始化聚類中心平面法向量和。

為了對算法性能進行評價，使用準確率（Accuracy）來衡量聚類性能。給定聚類標簽yi∈{1,2,…,k},i=1,2,…,m，其中m為數據點個數，k為簇數，計算相應的相似矩陣M∈Rm×m如下：

根據式（15），先利用數據集的真實聚類標簽計算得到相似矩陣Mt，再利用預測聚類標簽計算得到相似矩陣Mp。聚類算法的準確率定義為蘭德統計量（Rand statistic）：

其中，n00是Mp和Mt中0的個數，n11是Mp和Mt中1的個數。

為了驗證算法對噪聲的魯棒性，分別在無噪聲數據集和有噪聲的數據集上進行實驗。對于每個數據集，分別加入均值為0、標準差σ為0.05 和0.10 的兩種高斯噪聲生成帶有噪聲的數據集，σ為0表示無噪聲數據集。對于線性IRampTWSVC 算法，它在大多數數據集上均取得了較好的聚類準確率。以Spherical_5_2數據集的實驗結果為例，在無噪聲情形下，線 性KPC、KPPC、TWSVC、RampTWSVC 和IRampTWSVC的聚類準確率分別為80.20%、74.50%、85.07%、83.48%和85.58%；在標準差σ為0.05 的噪聲情形下，聚類準確率分別為78.69%、74.15%、69.09%、81.99%和85.17%；在標準差σ為0.10 的噪聲情形下，聚類準確率分別為77.59%、72.54%、75.77%、83.76%和86.44%。總體而言，線性IRampTWSVC算法在無噪聲、標準差σ為0.05 和標準差σ為0.10 的噪聲情形下，在13 個實驗數據集上分別取得了12個、11個和10個最好的聚類準確率。另外，圖2分別給出了Spherical_5_2 數據集的無噪聲、標準差σ為0.05 和標準差σ為0.10 的有噪聲數據集的真實簇類圖，圖3和圖4分別給出了線性RampTWSVC和線性IRampTWSVC在這三種情形下的聚類效果圖。圖2～圖4的效果圖進一步驗證了線性IRampTWSVC算法的性能，對噪聲具有較好的魯棒性。

圖2 Spherical_5_2數據集的真實簇類圖Fig.2 Actual clusters in dataset Spherical_5_2

圖3 線性RampTWSVC在數據集Spherical_5_2上聚類效果圖Fig.3 Formation of clusters by linear RampTWSVC on dataset Spherical_5_2

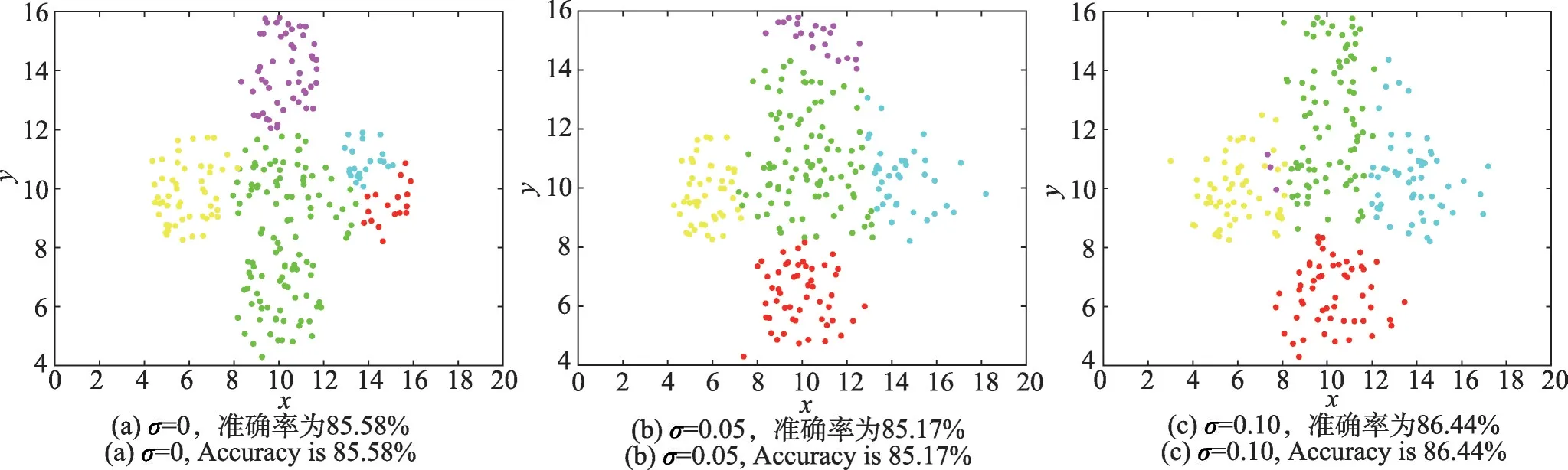
圖4 線性IRampTWSVC在數據集Spherical_5_2上聚類效果圖Fig.4 Formation of clusters by linear IRampTWSVC on dataset Spherical_5_2

表1 給出了非線性算法在所有數據集上的聚類準確率及次序，表中粗體數字表示最好的聚類準確率。從表1 的實驗結果不難發現，非線性IRampTWSVC算法在大多數數據集上取得了較好的聚類性能。對于Haberman 數據集，無噪聲情形下，非線性IRamp-TWSVC 的聚類準確率為72.57%，比KPC、KPPC、TWSVC 和RampTWSVC 分別高11.31 個百分點、11.62個百分點、11.93個百分點和6.51個百分點；在標準差σ為0.05 的噪聲情形下，非線性IRampTWSVC的聚類準確率為67.58%，比KPC、KPPC、TWSVC 和RampTWSVC 分別高6.01 個百分點、5.37 個百分點、7.24 個百分點和2.62 個百分點；在標準差σ為0.10的噪聲情形下，非線性IRampTWSVC 的聚類準確率為62.87%，比KPC、KPPC、TWSVC 和RampTWSVC分別高1.92 個百分點、1.92 個百分點、1.30 個百分點和0.98個百分點。這進一步說明了IRampTWSVC具有較好的魯棒性。根據表1中的聚類準確率的次序，計算非線性KPC、KPPC、TWSVC、RampTWSVC 和IRampTWSVC 的平均次序分別為3.76、4.12、3.59、2.19 和1.35，可以發現非線性IRampTWSVC 算法取得了最高的平均次序。為了說明各算法之間性能的差異，本文分別采用Friedman test 和Nemenyi test 方法檢驗IRampTWSVC算法與現有算法是否具有顯著性差異。根據Friedman test的定義[15]可得：

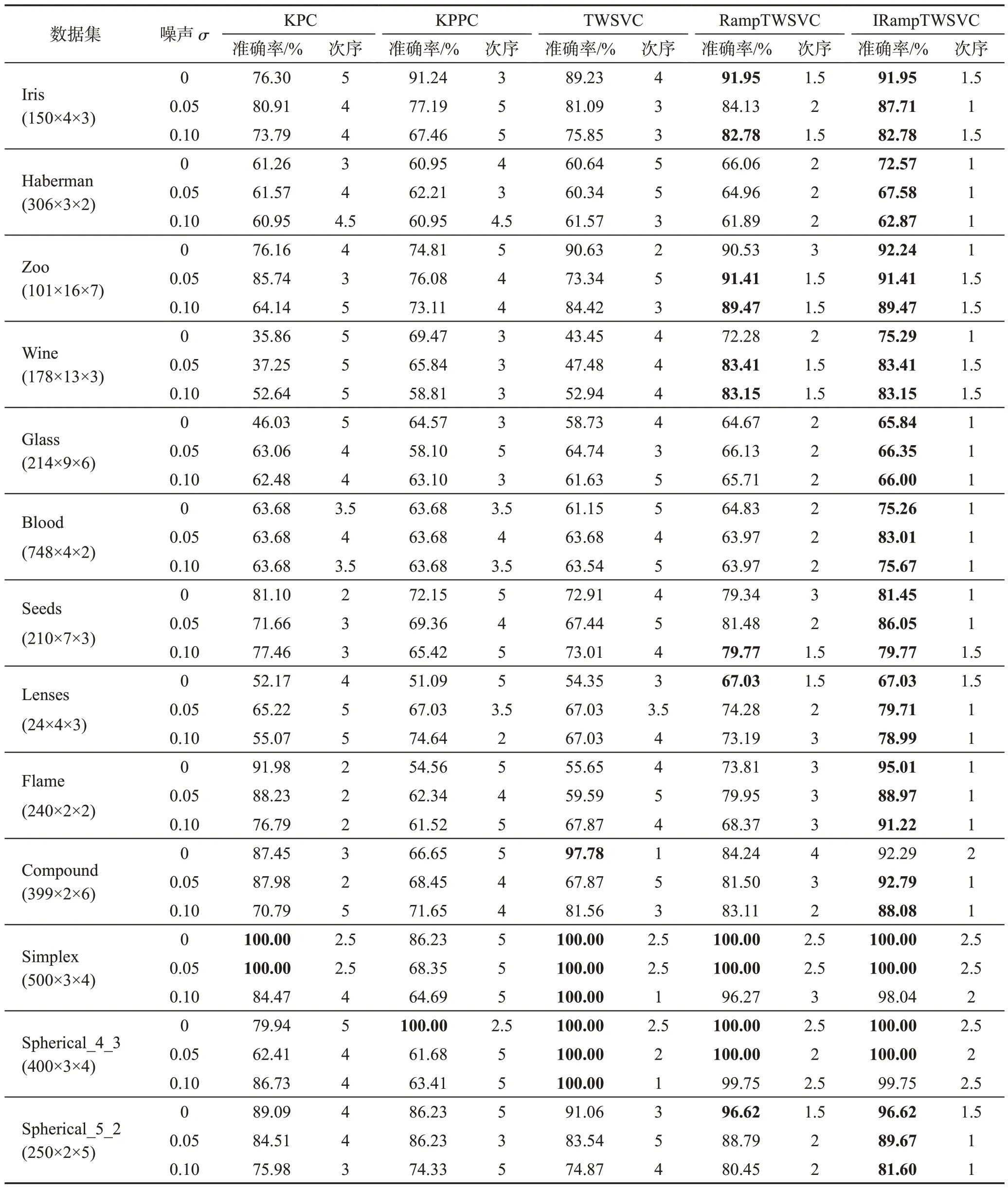
表1 非線性算法在所有數據集上的聚類準確率及次序Table 1 Clustering accuracy and rank of nonlinear algorithms on all datasets

其中，Ri是第i種算法在N個數據集上的平均排序，k表示算法的數量。于是，根據表1 知N=39,k=5，由式（17）和式（18）計算得≈87.651 7 和FF≈48.732 2。F分布的自由度為(k-1,(k-1)(N-1))=(4,152)，根據F分布臨界值統計表知，當α=0.05 時F(4,152)=2.431。因為FF=48.732 2>2.431，說明非線性IRamp-TWSVC算法優于其他算法。根據Nemenyi test的定義[15]，可得：

當α=0.05 時，qα=2.728，根據式（19）計算可得到相應的CD值為0.976 8。非線性IRampTWSVC與KPC、KPPC 和TWSVC 之間的平均次序差分別是3.76-1.35=2.41，4.12-1.35=2.77 和3.59-1.35=2.24，它們都大于CD值，這表明非線性IRampTWSVC 的性能明顯優于非線性KPC、KPPC和TWSVC；與非線性RampTWSVC 之間的平均次序差是2.19-1.35=0.84，它小于CD值，這表明非線性IRampTWSVC的性能雖然比非線性RampTWSVC 好，但它們之間的差異不夠顯著。

非對稱Ramp損失函數與Ramp損失函數的區別就在于引入了參數t，使Ramp 損失函數轉變為非對稱的形式，對位于聚類中心平面兩側的數據點采用不同的損失進行計算，使得遠離聚類中心平面的數據點對聚類中心平面的影響降低，并且通過調節參數t可以使模型具有更好的魯棒性。為了進一步分析IRampTWSVC 中所有參數對算法性能的影響（如圖5～圖7 所示），以Wine 和Spherical_4_3 數據集為例，首先討論參數t對線性IRampTWSVC 聚類性能的影響，固定參數cw和cb，參數t取值范圍為{0,0.1,0.2,…,1.0}。圖5 給出了參數t對線性IRamp-TWSVC 算法聚類準確率的影響，圖5（a）為Wine 數據集上的結果，圖5（b）為Spherical_4_3 數據集上的結果。從圖5（a）中可看出，當參數t取0.9時，聚類準確率最高；從圖5（b）中可看出，當參數t取0.6 時，聚類準確率最高。這表明了參數t對線性IRamp-TWSVC算法聚類準確率有較大的影響，充分體現了非對稱損失函數的優越性。類似地，再討論參數cw、cb對線性IRampTWSVC 算法聚類準確率的影響，此時固定參數t，參數cw和cb取值范圍為{-5,-4,-3,…,5}。圖6 給出了參數cw和cb對線性IRampTWSVC 算法聚類準確率的影響，圖6（a）為Wine數據集上的結果，圖6（b）為Spherical_4_3 數據集上的結果。實際上，參數t、cw和cb對非線性IRampTWSVC算法聚類準確率也有較大的影響，這里就不贅述了。最后，討論核參數μ對非線性IRamp-TWSVC 算法聚類準確率的影響，此時固定參數cw、cb和t，核參數μ取值范圍為{-5,-4,-3,…,5}。圖7 給出了核參數μ對非線性IRampTWSVC聚類準確率的影響。根據圖5、圖6和圖7 的結果，可以發現各參數對IRampTWSVC 聚類準確率都有較大的影響。本文采用了網格尋優的方法選擇最優參數，效率相對低下。因此，如何有效地選擇最優參數是值得進一步研究的問題。

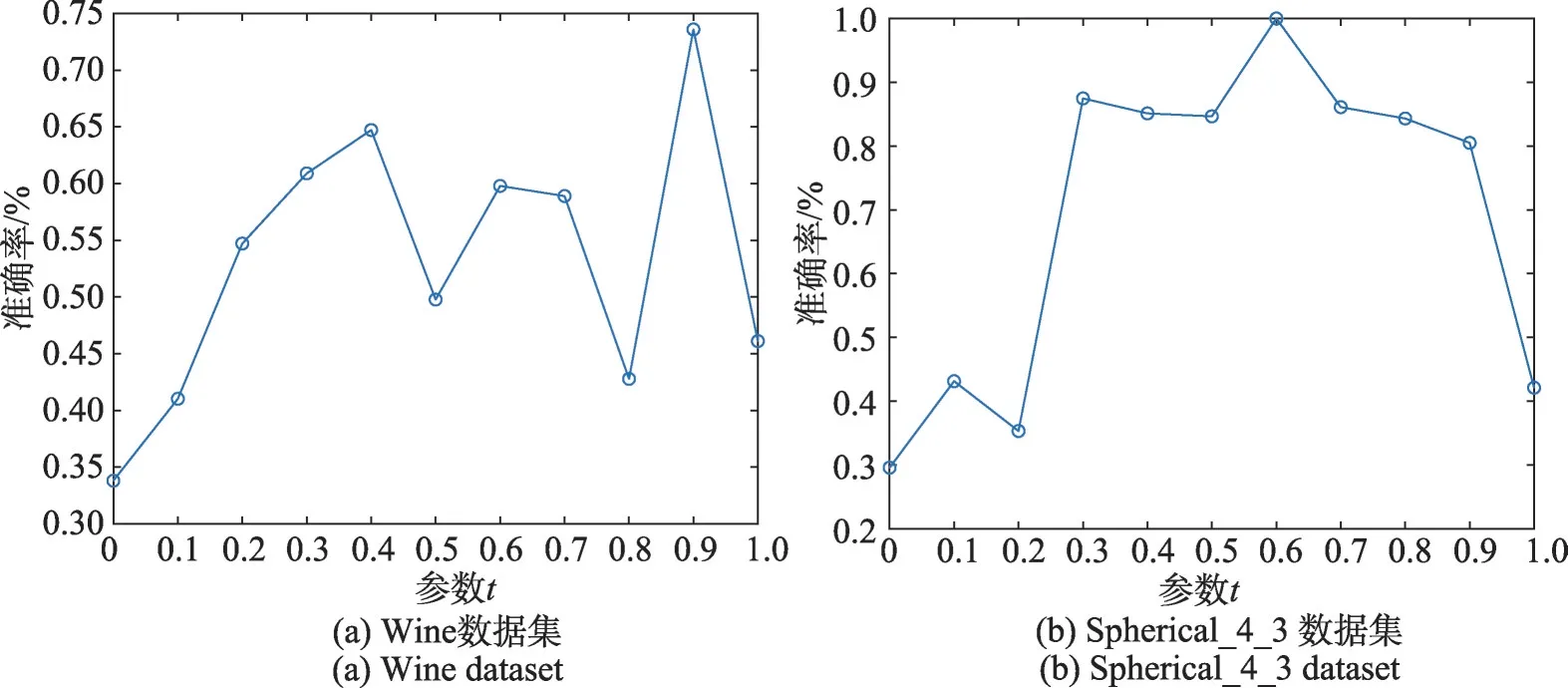
圖5 參數t 對線性IRampTWSVC算法聚類準確率的影響Fig.5 Influence of parameter t on clustering accuracy of linear IRampTWSVC

圖6 參數cw、cb 對線性IRampTWSVC算法聚類準確率的影響Fig.6 Influence of parameter cw,cb on clustering accuracy of linear IRampTWSVC

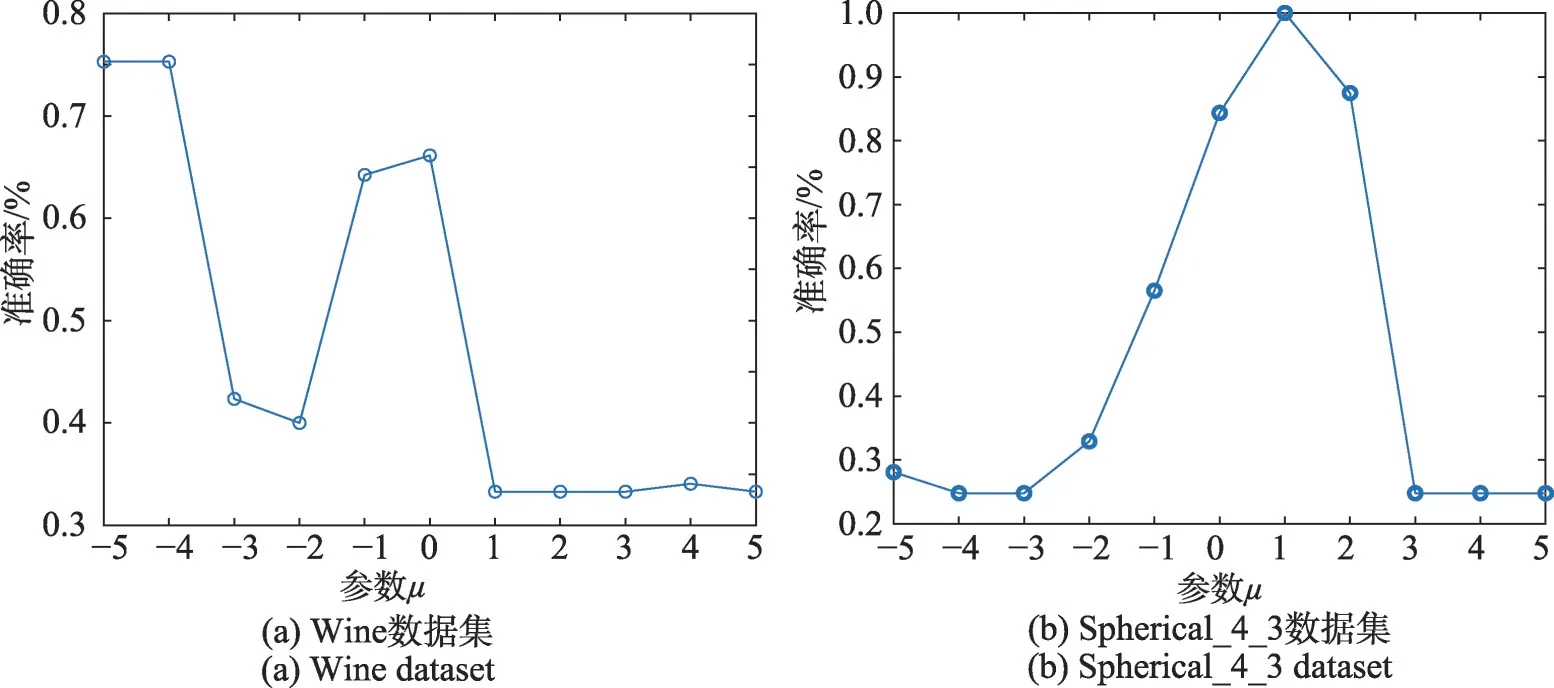
圖7 參數μ 對非線性IRampTWSVC算法聚類準確率的影響Fig.7 Influence of parameter μ on clustering accuracy of nonlinear IRampTWSVC

4 結束語

本文構造了一種非對稱Ramp損失函數，并在此基礎上提出了一種改進的Ramp 損失孿生支持向量機聚類（IRampTWSVC）。在多個UCI數據集和人工數據集上進行實驗，實驗結果驗證了本文算法的有效性。非對稱Ramp損失函數不僅繼承了Ramp損失函數的優點，而且參數t的引入使模型更加靈活，增強了IRampTWSVC 算法對噪聲的魯棒性。然而，本文算法依然存在一些不足：（1）該算法有多個參數，構建有效的最優參數選擇策略有待研究；（2）該算法通過交替迭代求解，每一個子問題都是一個二次規劃問題，本文雖然利用了SMO求解算法，但是當數據集規模較大時模型求解依然較慢，如何構建模型的快速求解算法也值得進一步研究。