基于吸脫附理論的RDX驅酸洗滌動力學模型研究

謝 強,陳厚和,李 慧

(1.安徽理工大學 化學工程學院,安徽 淮南 232001;2.南京理工大學 化學與化工學院,江蘇 南京 210094)

引 言

黑索今(RDX)是一種應用廣泛的單質高能炸藥[1-3],其生產能力與本質安全化程度直接影響著其應用。目前常用的RDX制造方法為直接硝解法與醋酸酐法。在RDX的直接硝解法生產制造過程中,由于硝化液的氧化過程與RDX的結晶過程同時進行,極易在結晶過程中于RDX晶體周圍包裹著含酸的氣泡[4-5]。此外,有學者[5-6]對RDX等一類硝胺炸藥的晶體形貌進行表征發現,其晶體存在著孔洞、凹坑麻點、溝槽、裂紋等缺陷,而且在這些缺陷中均充滿著硝酸的母液[7-8]。由此綜合導致了直接硝解法制造的RDX晶體含酸量較高。酸性粒子催化使得RDX貯存的危險性有所增加[9]。因此,研究RDX的驅酸洗滌動力學可為RDX驅酸洗滌的工藝參數優化與選擇提供理論依據。

目前針對RDX驅酸洗滌過程的研究主要集中在機理、數值模擬[10]、動力學等方面。如張幺玄等[11]對超聲波驅酸洗滌RDX的機理進行了探討,認為超聲波清洗器內的空化氣泡在RDX界面上發生了非對稱性潰滅,從而產生局部高速射流與渦流作用,強化了RDX驅酸清洗效果。2014年羅志龍等[12]基于RDX的超聲驅酸洗滌數據,假設驅酸過程符合一級動力學規律,采用最小二乘法進行了線性擬合,獲得了相關動力學參數。在此基礎上,2016年李婷婷等[13]對比分析了磁力常規清洗與超聲波清洗的動力學參數,常規清洗的表觀活化能大于超聲波清洗的表觀活化能,表明超聲洗滌更容易驅酸。然而,對其驅酸洗滌的動力學研究僅停留于假設的一級反應,由擬合效果來看,動力學模型描述的準確性不夠高。

基于此,本研究以吸附、擴散等理論為出發點,基于相應理論的動力學模型進行RDX驅酸洗滌的動力學探討,以獲得較為精確的動力學模型來較好地描述RDX驅酸洗滌過程,以期為RDX制造工藝參數優化提供較為準確的理論依據,為相關的工藝改進與連續化設計提供基礎。

1 驅酸洗滌動力學模型的建立

基于物理吸附與化學吸附的定義可知,由于RDX晶體表面存在著孔洞、凹坑麻點、溝槽、裂紋等缺陷且其晶體存在著非球形的菱與角,在含有硝酸的水溶液中RDX表面存在著不飽和力場。因此RDX表面自發地吸附硝酸與水。此外,因RDX與水、硝酸不存在化學反應,無任何形式的化學鍵,所以其吸附過程應為物理吸附,吸附力為RDX表面分子與硝酸分子、水分子間的分子間作用力。此外,陳剛[14]在對RDX表面吸附溶劑分子的研究過程中發現,溶劑分子與RDX晶面之間的吸附能主要是由靜電作用能和范德華作用能組成,且溶劑分子對RDX晶面的吸附是一個放熱過程。由于硝酸水溶液可作為RDX的溶劑,此研究結果同樣說明了RDX與硝酸水溶液之間的吸附不存在任何的化學變化。

由此可以推測,RDX表面酸脫除機制主要由兩個步驟組成:(1)RDX表面吸附的酸在吸收一定能量(能量大于吸附能)后從固體表面脫離;(2)脫離的酸由RDX晶體附近借助一定濃度梯度擴散遷移至溶液中。因此,在驅酸洗滌過程中,速率控制步驟有可能是其中一種或是兩種的綜合。

目前,國內外對固液吸附動力學模型與機理的研究有很多。在探索與實踐的歷程中,逐漸形成了6種典型且常用的動力學模型[15-17],包括基于溶液濃度的擬一階與擬二階動力學模型、Elovich方程模型、Freundlich方程模型、Avrami方程模型、H-S分數階動力學模型。結合脫附與吸附之間的可逆關系,此6種常用的脫附動力學模型如表1所示。

表1 常用的脫附動力學模型Table 1 Common desorption kinetic models

目前對質量擴散的動力學機理及其函數已有很多,如表2所示[18]。其擴散動力學模型為:

表2 常用的質量擴散動力學機理函數Table 2 Commonmass diffusion kinetic mechanism functions

(1)

(2)

式中:α為轉化率,即RDX表面酸的脫除率,見下式:

α=(qmax-qi)/(qmax-qe)

(3)

式中:qe為RDX表面吸附與脫附達到動態平衡時的酸度。

此外,不論是以脫附模型為主、還是以擴散模型為主,假設RDX的驅酸洗滌速率常數與溫度的關系服從阿倫尼烏斯方程,即:

k=Aexp(-E/RT)

(4)

式中:E為RDX表面脫酸的活化能。

在上述動力學模型進行非線性擬合的同時,需建立評選準則以選擇較優的RDX表面脫附動力學模型。因此采用全局優化的通用算法(UGO)將實驗數據與脫附動力學模型進行擬合。相關系數是選擇的首要衡量標準。其次的衡量標準為均方根誤差(RMSE)、確定系數(DC)和殘差平方和(RSS)。相關系數與DC越大,RMSE與RSS越小,則說明模型擬合程度越高。這些參數可由式(5)～(7)獲得:

(5)

(6)

(7)

式中:qexp,i為第i個實測轉化率值;qpre,i為第i個預測的轉化率值;N為觀測的樣本數。

2 實 驗

2.1 實驗材料

RDX粗品,平均粒徑1.3mm,酸度約1.072%,自制;氫氧化鈉,分析純,國藥集團化學試劑有限公司;酚酞,分析純,上海三愛思試劑有限公司。

2.2 實驗裝置

經過實驗室直接硝解法合成RDX的步驟與抽濾后,得到RDX粗品。然后將裝有一定量的RDX粗品與去離子水的燒杯放置于集熱式磁力攪拌加熱器與超聲波清洗機內,在不同的洗滌溫度下分別進行不同清洗時間的實驗。隨后將驅酸洗滌實驗后的RDX經抽濾后得到含酸濾餅。最后,將濾餅均勻分散于去離子水中,滴加酚酞指示劑,并使用裝有氫氧化鈉標準溶液的微量滴定管進行酸度測定。濾餅酸度計算公式為:

(8)

式中:q為濾餅酸度(%);c為氫氧化鈉標準溶液的濃度(mol/L);V1為空白實驗所需氫氧化鈉標準溶液的體積(L);V2為滴定濾餅所需氫氧化鈉標準溶液的體積(L);m為濾餅質量(g)。

實驗流程與裝置如圖1所示。

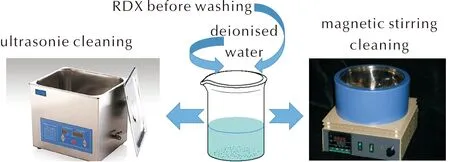
圖1 RDX驅酸洗滌動力學實驗流程與裝置Fig.1 The kinetic test process and device of washing RDX

2.3 實驗過程

為了研究RDX驅酸洗滌動力學,在20、25、30、35、40℃的洗滌溫度下分別進行不同清洗時間的實驗(超聲清洗時間分別為10、20、40、60、80min,加熱攪拌清洗時間分別為10、40、70、100、130min)。為了與李婷婷等[13]研究的結果進行對比分析,其他實驗條件均為一致:兩種清洗方式的液固比均為2∶1,超聲清洗頻率為25kHz,超聲功率為85%,攪拌速率為150r/min。然后基于不同溫度下不同清洗時間的酸度值及6個脫附模型和9個擴散模型,采用共享參數模式下非線性擬合方法進行驅酸洗滌動力學參數的求解。其中,針對脫附模型中可轉換為積分形式的模型1、2、5、6來說,采用共享參數模式下非線性擬合方法進行求解;針對不可轉換積分形式的模型3來說,可采用共享參數模式下常微分方程參數擬合方法進行求解;針對不可轉換積分形式的模型4來說,微分方程求解器無法進行計算。此外,針對9個擴散模型來說,基于不同機理函數的積分形式將實測數據進行轉化,隨后采用共享參數模式下非線性擬合方法進行求解。

共享參數模式下非線性擬合方法,即在具有共同的擬合參數且含有隨不同數據文件而變化的常數情況下采用的一種非線性擬合方法,可通過1stOpt軟件實現。以脫附模型6與磁力攪拌加熱清洗方式獲得的5種溫度條件下的數據為例進行說明,其共有4個擬合參數(脫附活化能E、指前因子A、脫附時間指數n、脫附模型常數m),洗滌溫度(20、25、30、35、40℃)即為隨不同數據而變化的常數。

3 結果與討論

3.1 脫附模型的優選

不同溫度下兩種清洗方式的脫附模型擬合狀態參數間的對比如圖2所示。基于R與DC參數均為最大且RMSE與RSS均為最小的選擇原則,黑色柱形則表示最優的模型。擬合較優模型的動力學參數見表3。

圖2 不同溫度下兩種清洗方式的脫附模型擬合狀態參數對比Fig.2 Comparison of fitting parameters of desorption models for two washing methods at different temperatures

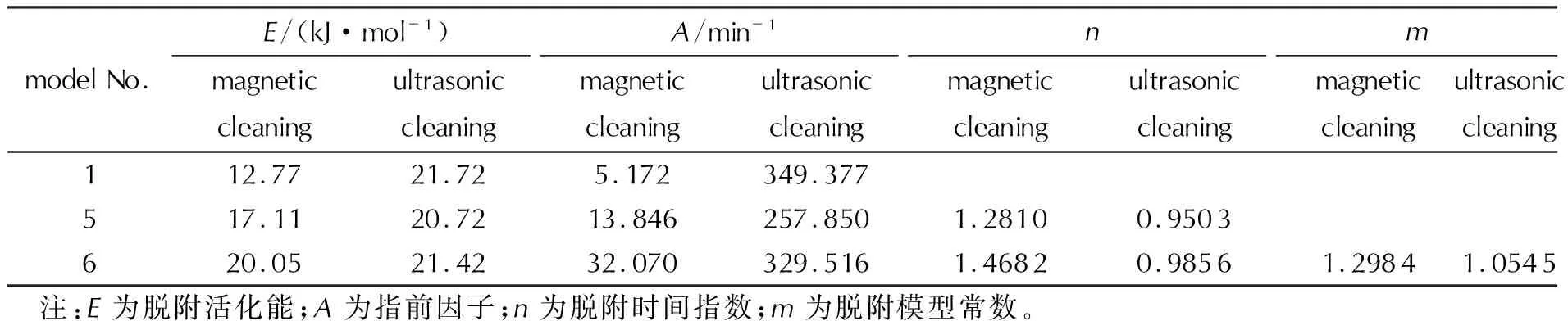
表3 兩種清洗方式的較優脫附模型擬合參數Table 3 The better fitting parameters of desorption models for two washing methods

由圖2可知,在20、25、30、35、40℃的清洗溫度下,磁力攪拌清洗的最優脫附模型分別為模型6、6、5、6、6,而超聲波清洗的最優脫附模型分別為模型1、1、1、6、6。此外,還可以看出,對磁力攪拌清洗來說,模型5、6的擬合狀態參數大都相近;而對超聲波清洗來說,模型1、5、6的擬合狀態參數大都相近,由表3可看出,模型5、6的脫附時間指數n均接近于1且模型6的脫附常數m也接近于1。綜上所述,模型6(即H-S分數階脫附動力學模型)能夠更好地、統一地描述兩種清洗方式的驅酸洗滌過程。對磁力攪拌來說,擬合決定系數R與DC均在0.999以上、RMSE均小于0.012、RSS均小于0.0008;對超聲波清洗來說,擬合的R均在0.998以上、DC均在0.993以上、RMSE均小于0.031、RSS均小于0.006。

3.2 擴散模型的優選

不同溫度下兩種清洗方式的擴散模型擬合狀態參數(R、DC、RMSE、RSS)分布云圖如圖3與圖4所示。其中模型9的機理函數積分形式將擬合的因變量進一步擴大,基于RMSE與RSS的定義與計算公式,因變量的擴大直接導致RMSE與RSS的值擴大,使得RMSE與RSS的衡量準則失效,故在圖3與圖4中,舍去模型9的RMSE與RSS值。此外,由于在擴散模型擬合中,因變量的值與機理函數的積分形式關系密切,因此擴散模型的優選性僅能使用作為相對值的R與DC來衡量。

圖3 不同溫度下磁力攪拌驅酸洗滌擴散模型的擬合狀態參數云圖Fig.3 Cloud map of fitting parameters of diffusion models for the magnetic stirring cleaning at different temperatures

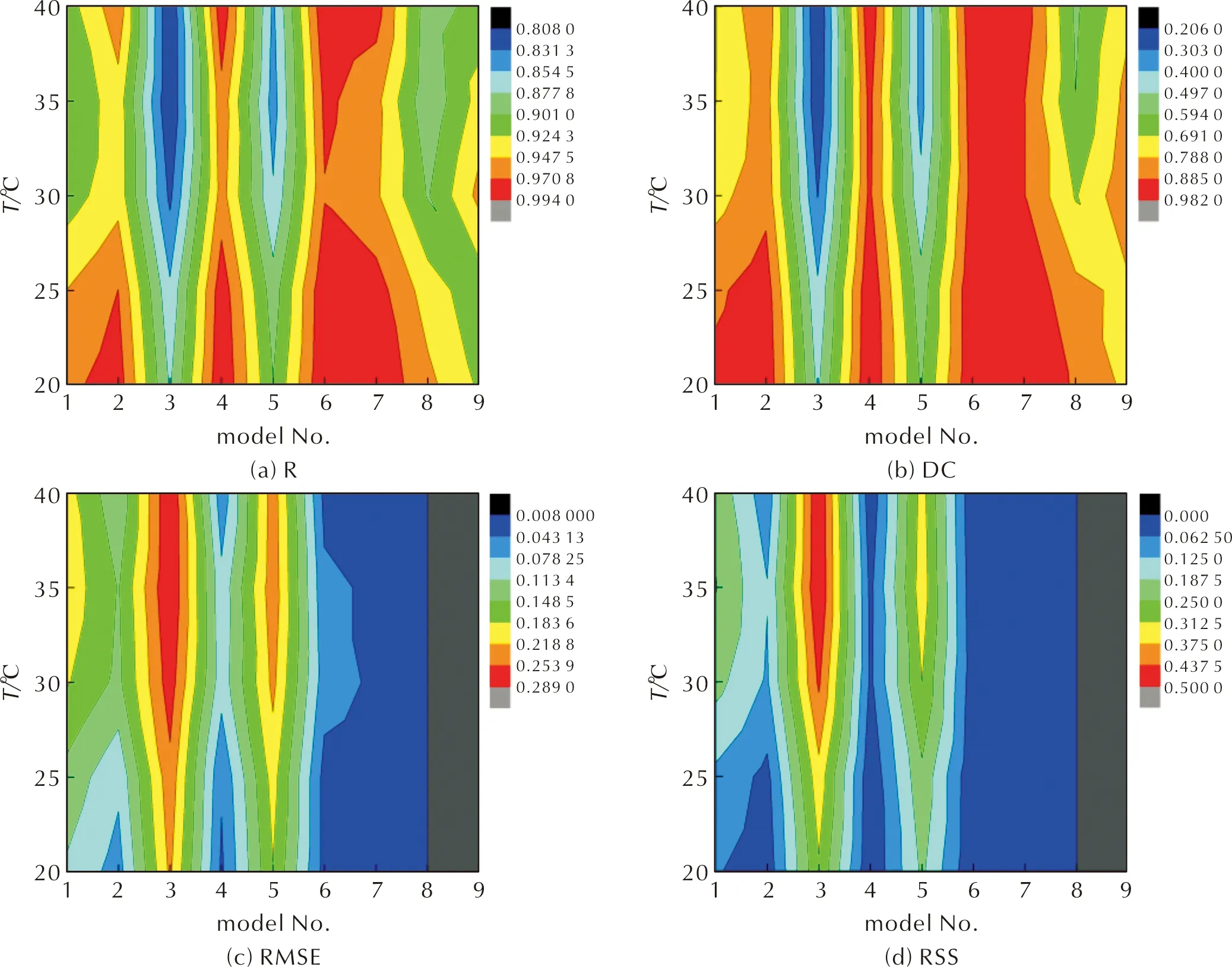
圖4 不同溫度下超聲驅酸洗滌擴散模型的擬合狀態參數云圖Fig.4 Cloud map of fitting parameters of diffusion models for the ultrasonic cleaning at different temperatures

如圖3所示,針對不同洗滌溫度下的磁力攪拌清洗來說,相關系數R的云圖中僅在模型6位置出現“紅色縱向貫穿”的現象,而在DC的云圖中出現“紅色縱向貫穿”的位置位于模型4、6、7,在RMSE、RSS的云圖中出現“藍色縱向貫穿”的位置位于模型6、7、8。因此用來描述磁力攪拌驅酸過程的最優模型為模型6。

由圖4可知,在R云圖中,雖未出現“紅色縱向貫穿”,但在模型6的位置時縱向紅色區域較多,在DC的云圖中出現“紅色縱向貫穿”的位置位于模型4、6、7,在RMSE的云圖中藍色區域的現象與圖4相應的云圖一致,在RSS云圖中,出現“藍色縱向貫穿”的位置位于模型4、6、7、8。因此,最優的超聲波驅酸洗滌擴散模型為模型6。

綜上所述,擴散模型6,即Jander方程V類,能夠更好且統一地描述兩種清洗方式驅酸洗滌過程,其動力學相關參數為:當洗滌方式為磁力攪拌時,活化能為13.49kJ/mol,指前因子為0.973min-1;當洗滌方式為超聲波清洗時,活化能為11.02kJ/mol,指前因子為0.569min-1。

3.3 最優驅酸洗滌模型的選擇

由上述對脫附模型與擴散模型的分析可得,兩種較優的動力學方程如下式所示:

(9)

(10)

將上述兩式變化為:

(11)

qi=qmax{1-[Aexp(-E/RT)t]1/2}3

(12)

基于兩種清洗方式的實驗數據,將以脫附模型6與擴散模型6得到的預測曲線進行對比分析,其結果如圖5和圖6所示。

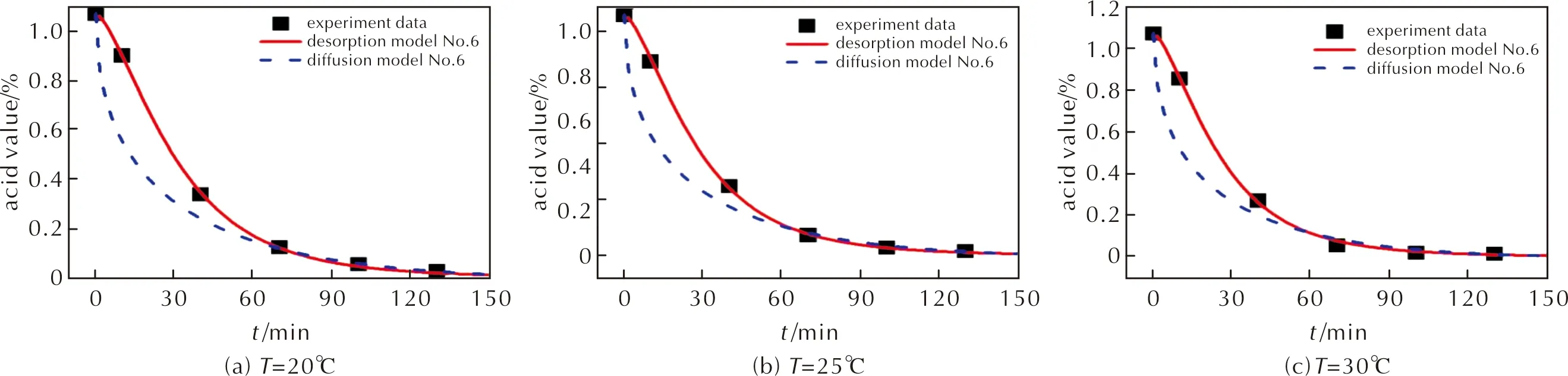
圖5 磁力攪拌清洗數據與脫附模型及擴散模型對比Fig.5 Comparison of data from experiments, the desorption model and the diffusion model for the magnetic stirring cleaning

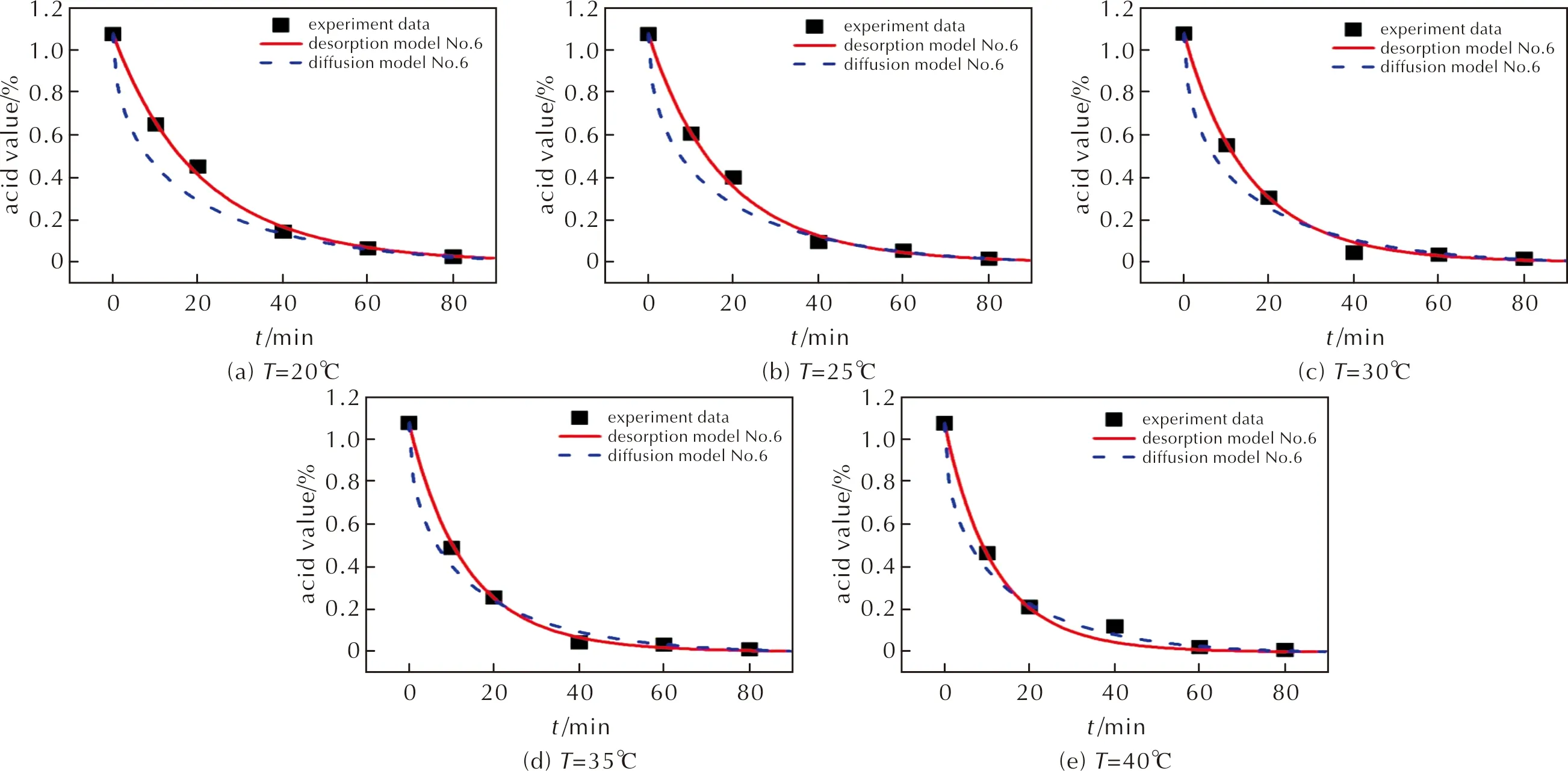
圖6 超聲波清洗數據與脫附模型及擴散模型對比Fig.6 Comparison of data from experiments, the desorption model and the diffusion model for the ultrasonic cleaning

由圖5和圖6可知,脫附模型6的預測曲線均更接近于實驗數據,且擬合的相關系數均在0.998以上,高于李婷婷等[13]的擬合結果。結果表明,用來描述的RDX驅酸洗滌過程的最優動力學模型為脫附模型6,即H-S分數階脫附動力學模型。此外,還可以看出,隨著溫度的升高,擴散模型越接近于脫附模型。這是因為洗滌溫度增加,由于脫附活化能高于擴散活化能,RDX表面脫附速率增長的幅度較大,從而導致其驅酸洗滌過程的速率控制步驟由脫附為主的綜合過程逐步轉化為酸的擴散過程。

綜上所述,RDX的驅酸洗滌動力學模型如式(13)所示:

(13)

式中:當洗滌方式為磁力攪拌時,E=20.05kJ/mol、A=32.070min-1、n=1.4682、m=1.2984;當洗滌方式為超聲波清洗時,E=21.42kJ/mol、A=329.516min-1、n=0.9856、m=1.0545。

此外,在式(13)中,脫附時間指數n體現了RDX驅酸洗滌過程中可能存在的復雜脫附機理綜合作用。

將超聲波清洗的動力學參數與磁力攪拌的情況相比(見表3),其表觀活化能的值僅增加了1.37kJ/mol,變化較小,而指前因子的值約提高了9倍。雖然超聲波清洗的脫附活化能稍高,但其指前因子的增加非常明顯,兩種清洗方式的酸脫除速率常數對比如圖7所示。

圖7 兩種清洗方式的酸脫除速率常數對比Fig.7 Comparison of rate constants of removal acid for two washing methods

由圖7可知,當洗滌溫度為20～50℃時,與磁力攪拌清洗相比,超聲波清洗時的速率常數增加了4.86～5.17倍。結果表明,雖然超聲清洗的脫附能壘稍高,但即將脫附的酸活性位點數目較大,總體來說,反應速率常數較大。此結果主要因為,超聲波的引入使其空化效應在含RDX粗品的水溶液中進行作用,從而引起溶液的湍動效應與微擾效應,即空化效應產生的聲沖擊波引起溶液宏觀湍流并于RDX晶體缺陷邊界發生氣泡破裂引起局部的微射流。而磁力攪拌僅是通過攪拌葉輪轉動引起溶液的湍流效應。兩者相比,超聲波清洗較大幅度地提高了RDX表面吸附的酸脫效率。

4 結 論

(1)H-S分數階脫附模型能夠較為準確地描述RDX驅酸洗滌過程,其擬合相關系數均在0.998以上、擬合決定系數均在0.993以上。

(2)在本研究的實驗條件下,當洗滌方式為磁力攪拌時,脫附活化能為20.05kJ/mol、指前因子為32.070min-1、脫附時間指數為1.4682、脫附模型常數為1.2984;當洗滌方式為超聲波清洗時,脫附活化能為21.42kJ/mol、指前因子為329.516min-1、脫附時間指數為0.9856、脫附模型常數為1.0545。

(3)當洗滌溫度為20～50℃時,與磁力攪拌清洗相比,超聲波清洗時RDX表面吸附的酸脫除速率約增大了4.86～5.17倍,且隨著洗滌溫度的升高,驅酸洗滌過程的速率控制步驟逐漸由脫附為主的綜合過程逐步轉化為酸的擴散過程。