大規模三維頻率域電磁積分方程法數值模擬

肖調杰,周 峰,鄭翾宇,劉 劍,陳 琳,劉 杰,易明寬, 陳旭光,龔春葉,4,楊 博,甘新標,李勝國,左 克

(1.國防科技大學計算機學院,湖南 長沙 410073;2.國防科技大學高端裝備數字化軟件實驗室,湖南 長沙 410073; 3.東華理工大學地球物理與測控技術學院,江西 南昌 330013;4.國家超級計算天津中心,天津 300457)

1 引言

地電磁學中的頻率域電磁法是一類重要的地球物理方法,其通過觀測由不同頻率天然場源或人工場源激發的電磁場在地下介質中產生的感應二次場,并分析其分布規律,進而獲得地下電性分布特征及相關電性結構參數[1-4]。頻率域電磁法種類繁多,包含大地電磁測深法、可控源音頻大地電磁法、海洋可控源電磁法等主動源方法以及大地電磁法、音頻大地電磁法、甚低頻法等被動源方法,具有探測深度大、分辨率高及抗干擾能力強等優點,在地球深部結構探測、地熱勘探、礦產與油氣勘查及環境與工程勘探等諸多領域有著廣泛的應用[5-10]。

數值方法和線性方程組求解是頻率域電磁法數值模擬的2個重要方面。一方面,有限單元法、有限差分法和積分方程法等是當前頻率域電磁法中使用最為廣泛的3種數值模擬方法[11-17]。其中有限單元法和有限差分法屬于微分方程法,基于Maxwell方程的微分形式,求解時需要將全域作為計算區域,會造成較大的未知量和計算量,當模型規模較大時,其計算自由度可迅速增加至數千萬、數億量級甚至更大。積分方程法基于Maxwell方程的積分形式,是數值模擬算法中應用得最早的一種方法。采用積分方程法計算電磁響應時,只需對目標異常體進行剖分,相比于有限單元法和有限差分法,積分方程所需求解的未知量大大減少。由于引入了格林函數,積分方程法避免了微分方程法中場值傳遞造成的累積誤差,并且不需要施加吸收邊界條件或截斷邊界條件,從而避免了截斷邊界誤差,其數值結果具有半解析解的較高精度[18,19]。另一方面,相比于迭代法獲得近似解,直接解法可以獲得精確解。在三維數值模擬中,線性方程組求解占據了大部分計算量,求解速度直接關系到三維數值模擬的計算速度。目前方程組求解可以分為直接解法和迭代解法。迭代解法通過迭代過程中的不斷修正來獲得線性方程組的近似解。相比迭代解法,直接解法計算量非常大,且需要大量存儲空間,但是對于解存在的線性方程組,直接解法總能夠在有限的時間內獲得其精確解,且具有非常高的穩定性[20,21]。

當前,頻率域電磁積分方程法數值模擬存在內存受限和計算速度慢等問題,而大規模模型多頻點、多場點的計算已成為其實際應用中的瓶頸。隨著Harrington[22]在1968年提出了矩量法,此后積分方程法在計算電磁領域得到了快速發展。而在三維地電領域,Hohmann[23]在1975年基于六面體網格闡述了奇異核積分技術,開啟了將積分方程法用于求解三維地電問題的大門,隨后Weidelt[24]推導得到了層狀介質張量格林函數的積分表達式,奠定了積分方程法在地電問題中的應用基礎。之后,諸多研究人員對積分方程法在頻率域電磁法中的應用開展了大量的研究[10,12]。積分方程法在求解過程中需要求解稠密線性方程組,若求解區域的未知量為W,則其存儲需量為O(W2),直接求解的計算復雜度為O(W3),隨著計算規模的增大,面臨著內存受限和計算速度慢等問題。在優化存儲方面,Ting等[25]提出利用格林函數的對稱性來減少系數矩陣的存儲,但是隨著模型網格數量的進一步增大,依然面臨著內存受限的問題。在提高計算速度方面,Wannamaker等[26]基于大網格單元的格林系數插值出小網格單元的格林系數來加快獲得格林系數矩陣;Aksun[27]、袁建生等[28]采用復鏡像法加快格林函數的計算。為加快方程組的求解速度,Tripp等[29]把系數矩陣拆分成了若干個小矩陣,Millard等[30]提出了穩定雙共軛梯度的快速傅里葉變換法。此外,Zhadnov等[31,32]、Abubakar等[33]、Ueda等[34]和Kruglyakov等[35]深入研究了Born近似、擬線性近似等方法,以降低求解精度為代價提高了計算速度。而隨著計算規模、場點和頻點的迅速增加,所需內存和計算量將急劇遞增。上述研究在一定程度上緩解了內存受限和計算速度慢的問題,但未能從根本上給出合理的解決方案。

因此,本文面向頻率域電磁場數值模擬,采用積分方程法、分布式存儲和直接解法等技術,設計了一種多層級多粒度混合并行策略,解決了內存受限和計算速度慢等問題,實現了頻點間并行、阻抗矩陣并行填充、方程組并行求解的快速、高精度、高可擴展性的頻率域電磁三維積分方程數值模擬方法。

2 物理模型

圖1所示為頻率域電磁法三維地電模型示意圖。在地表有一接地導線作為電性發射源(Transmitter),源的長度為L,發射電流為I。積分方程法求解范圍是電磁參數區別于背景介質的異常區域,圖1中所示背景區域是電導率為σb的均勻半空間,其中存在電導率為σ的異常區域。給定發射源、介質電性參數及空間幾何等信息,可通過數值模擬計算得到整個空間的電磁場分布。

Figure 1 Diagram of geo-electromagnetic model圖1 三維地電模型示意圖

3 積分方程法

研究任何形式的電磁場都必須從Maxwell方程組出發,電磁場通過傅里葉變換,可將時間域的電磁場轉換為一系列諧變場的組合,取時諧因子為e-iwt,在準靜態條件下,Maxwell方程組變為式(1)～式(4)[5]:

×E=iωμΗ

(1)

×H=(σ-iωε)E+Js

(2)

·εE=ρ

(3)

·μH=0

(4)

其中,E是電場強度矢量,H是磁場強度矢量,ρ是自由電荷密度,ε是介質的介電常數,μ是介質磁導率,σ是介質的電導率,Js是激發源,ω=2πf是角頻率,f是頻率,i是虛數單位。

對式(1)求旋度后,結合式(2),可得到電場雙旋度方程,如式(5)所示:

××E-iωμ(σ-iωε)E=iωμJs

(5)

根據疊加原理,將總電場分解為入射電場Einc和散射電場Esca,有:

E=Einc+Esca

(6)

采用電張量格林函數,并結合式(5),可以得到積分公式,如式(7)所示:

(7)

其中,Ωs是場源積分區域,Ω是異常體積分區域,G是并矢Green函數。當背景模型為均勻半空間時,G是均勻半空間并矢Green函數;當背景模型為層狀介質時,G是層狀介質并矢函數[25,26]。

在進行數值模擬之前,需要對式(7)進行剖分離散。本文采用四面體單元,將異常體離散成N個四面體子單元。采用適用于介質的體積分方程法,假設每個單元內部的電導率和電場保持不變,取為單元中心ri(i=1,2,…,M)處的值(如圖2所示,其中Ex,Ey和Ez分別為x,y和z方向的電場強度),可得式(8):

E(rm)=Einc(rm)+

(8)

其中,Ei為單元中心處的電場。

Figure 2 Diagram of tetrahedral element圖2 四面體單元示意圖

將式(8)寫成矩陣形式,可形成關于異常體區域3N個未知電場的線性方程組,如式(9)～式(12)所示:

A·E=Einc

(9)

(10)

(11)

(12)

求解式(8),可得到異常體區域的電場值。而最終某一點的總場由該點的入射場和散射場疊加而成,再通過式(8)即可獲取空間中任一點處的電場值。

4 并行策略

4.1 多級并行架構

在計算之前,采用國產網格剖分軟件YH-Grid或開源軟件Tetgen對模型進行網格離散,并準備好相應的輸入文件。電磁法的頻點間計算無數據依賴關系,具有天然的可并行性。對單頻點的串行算法進行計算時間占比分析,發現其阻抗矩陣填充、方程組求解和觀測點場值計算占總計算時間90%以上。圖3為本文設計的并行算法流程示意圖。首先,采取進程分組的方式將不同頻點劃分到不同的進程組。然后,各進程組的主進程讀取輸入文件并廣播給組內所有進程。接著,并行填充阻抗矩陣A,采用分布式存儲。最后加入邊界條件,對方程組進行并行求解。求解方程組之后,可進一步對觀測點的場值進行并行計算。最后進行數據收集和后處理。

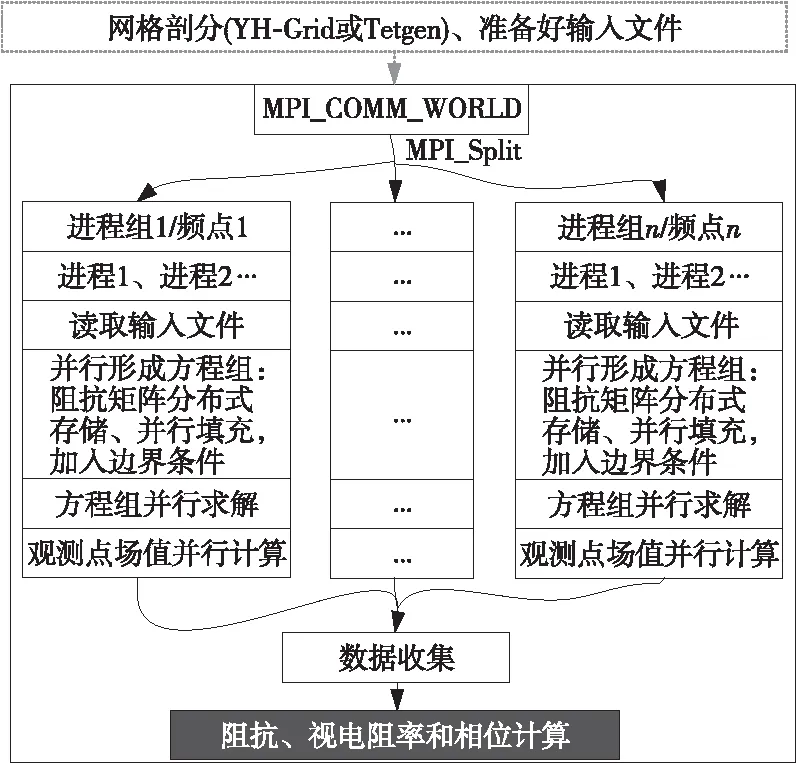
Figure 3 Flow diagram of multi-level parallel algorithm圖3 多級并行算法流程示意圖

4.2 負載均衡

為保持良好的負載均衡與可擴展性,采取分布式存儲,采用廣泛應用在ScaLAPACK、SLATE、MAGMA等稠密線性代數庫中的二維Block- cyclic數據映射方法。假設一共有N個四面體單元,則阻抗矩陣A的大小為3N×3N。將矩陣元素以塊的形式不重復地循環分配/存儲在P×Q個不同進程之中,其中P和Q分別為二維進程網格中垂直方向和水平方向的進程個數。二維進程網格如圖4所示,在邏輯上將9N2個矩陣元素分成一個個大小為mb×nb的分塊小矩陣,其中每個格子代表一個分塊小矩陣,相同顏色的分塊小矩陣存儲在同一個進程中,每個進程保存的矩陣元素個數為9N2/(P×Q),一般要求緩存M≤9N2/(P×Q)。

Figure 4 Block-cyclic mapping圖4 Block-cyclic映射

設當前進程在進程網格中的索引為(my_row,my_col),圖4a中矩陣元素的全局索引為(ig,jg),圖4b中當前進程中矩陣元素的局部索引為(il,jl),索引從0開始,則有:

my_row=(ig/mb)%P

(13)

my_col=(jg/nb)%Q

(14)

當前進程局部索引和全局索引之間的關系滿足式(15)～式(18):

il=(ig/mb)/P×mb+ig%mb

(15)

jl=(jg/nb)/Q×nb+jg/nb

(16)

ig=P×mb×(il/mb)+il%mb

(17)

jg=Q×nb×(jl/nb)+jl%nb

(18)

4.3 網格分發

根據式(10)可知,阻抗矩陣A由四面體兩兩之間的相互關系系數矩陣組合而成,如圖5所示,每個四面體單元都對應3行和3列。

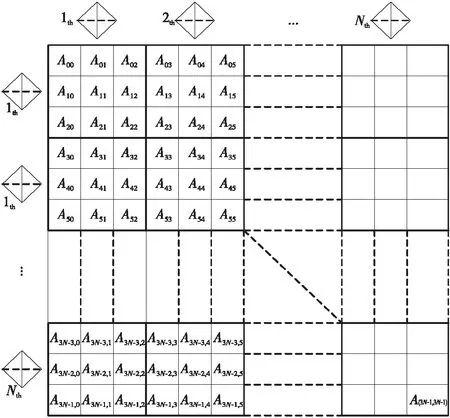
Figure 5 Impedance matrix A圖5 阻抗矩陣A

以總進程為6、P×Q=2×3、阻抗矩陣A分成9×9個分塊小矩陣Tij(i=0,…,8;j=0,…,8)為例,每個分塊小矩陣大小為NB×NB,Tij如式(19)所示:

(19)

如圖6所示,按照塊循環(block-cyclic)方式將阻抗矩陣A映射到2×3的進程網格中。

Figure 6 Impedance matrix圖6 阻抗矩陣分布示意圖

如圖7所示,將每行或每列塊(block)對應的單元網格信息存放在一個包(bucket)中,矩陣塊是方陣,第i行block和第i列block涉及到的網格單元相同,對應同一個bucket,在圖中不做展示。其中每個四面體需要保存其全局編號(index)、屬性編號(id)、4個節點位置信息(P0(x0,y0,z0),P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)),即2個整數和12個浮點數,分別為(index,id,x0,y0,z0,x1,y1,z1,x2,y2,z2,x3,y3,z3)。

Figure 7 Grid distribution圖7 網格分發

根據圖6b,進程(0,0)存儲的矩陣塊如圖8所示,進程(0,0)所存儲的矩陣塊為T0,0,T0,3,T0,6,T2,0,T2,3,T2,6,T4,0,T4,3,T4,6,T6,0,T6,3,T6,6,T8,0,T8,3,T8,6,填充Tij需要第i和第j個bucket,其中行涉及到的bucket為第0,2,4,6和8個bucket,列涉及到的bucket為第0,3和6個bucket。因此,一起需要第0,2,3,4,6和8個bucket。將行和列涉及到的bucket指針分別保存在rowGrid和colGrid2個不同的數組中。一般地,第i個bucket由進程(i%P,i%Q)進行廣播。首先,負責讀入網格和切分網格到bucket的主進程將第i個bucket發送給進程(i%P,i%Q),再由該進程在row_comm和col_comm分別廣播,行進程號等于i%P的進程將收到的bucket指針保存在rowGrid中。列進程號等于i%Q的進程將收到的bucket指針保存在colGrid中,即完成網格分發。

其中,負責廣播的進程保存的bucket指針同時保存在rowGrid和colGrid中。本文引入isBoth的哈希表進行判斷,以避免內存重復釋放。

Figure 8 Matrix block of process (0,0)圖8 進程(0,0)存儲的矩陣塊

4.4 阻抗矩陣填充

網格分發完成之后,各進程已得到所需網格信息。接下來,只需要在rowGrid和colGrid中對每個四面體分別進行計算,然后保存到本地阻抗矩陣即可。假設rowGrid有m個bucket,colGrid有n個bucket,阻抗矩陣填充如算法1所示[36]。

算法1阻抗矩陣填充

輸入：m個bucket組成的網格塊rowGrid和n個bucket組成的網格塊colGrid。

輸出：本地阻抗矩陣A。

forj=0:ndo

fori=0:mdo

Aptr=A+i*NB+j*NB*ld;/*跳轉到對應NB塊的首地址*/

nElement←colGrid的四面體個數;

mElement←rowGrid的四面體個數;

fork=0:nElementdo

計算本地填充的列方向開始位置n0和結束位置n1;

forp=0:mElementdo

計算本地填充的行方向開始位置m0和結束位置m1;

計算四面體之間產生的矩陣T;

Aptr(m0:m1,n0:n1)←

T(m0:m1,n0:n1);

endfor

endfor

endfor

endfor

4.5 復數稠密線性系統LU分解

積分方程法最終形成一個線性稠密的復數線性方程組,根據式(10)可知,采用部分選主元的LU分解進行求解[37],如式(20)所示:

(20)

其中,A11∈CNB×NB,A12∈CNB×(N-NB),A21∈C(N-NB)×NB,A22∈C(N-NB)×(N-NB)。

4.6 觀測場值并行計算

已知異常體各離散單元的場值,便可根據式(8)求得任意觀測點處的場值。各觀測點的場值為背景場與二次場之和,其中二次場為地下異常體在該處產生的感應場值,由異常體中各四面體在該處產生的場值累加組成。當模型規模較大、觀測點數較多時,觀測點處的場值計算耗時巨大。考慮到實際應用場景,進程數通常少于觀測點數,因此在各進程組/單個頻點內對觀測點處的場值進行并行計算。采用主從模式的并行加速策略,各進程組內主進程負責任務調度和結果收集,從進程負責計算并向主進程返回計算結果。計算流程如圖9所示。

Figure 9 Flow chart of parallel calculation of field at observation points圖9 觀測點場值并行計算流程圖

5 驗證與測試

5.1 正確性和準確度驗證

如圖10所示,在電導率為0.02 S/m的均勻半空間中有一個電導率為0.2 S/m的低阻體。低阻體的埋深為100 m,尺寸為120 m × 200 m × 400 m,中心坐標為(0 m,1 000 m,300 m)。偶極子源沿y方向,長度為1 m,發射電流為100 A,頻率為3 Hz,中心坐標為(0 m,0 m,0 m)。沿y軸方向在異常體上方布設間距為20 m的41個觀測點,起點位置為(0 m,600 m,0 m),終點位置為(0 m,1 400 m,0 m)。

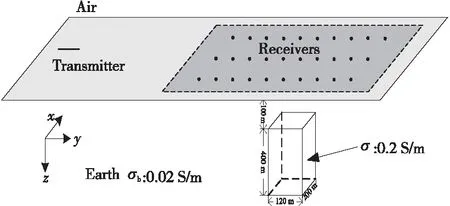
Figure 10 Testing model:There is a conductive body embedded in a half-space圖10 測試模型:均勻半空間中存在一低阻體

選取Ey的實部、虛部與前人結果[38]進行對比,如圖11所示,可以看到,實部和虛部的相對誤差在6%以內。

Figure 11 Comparison of electric field amplitudes圖11 電場振幅對比

Figure 13 Distribution of real component of Ey圖13 Ey實部分布

5.2 性能測試

以可控源為例,如圖12所示。按對數在10-1～102Hz均勻取16個頻點,共16 × 12495個未知量。若采用串行算法中的全存儲策略而不是本文中的分布式存儲,阻抗矩陣所需存儲空間大小為16×(12495×2)2×8/10243=74 GB,而隨著問題規模的增加,所需存儲空間會進一步極速劇增。因此,采用本文算法,在天河高性能計算系統上進行測試,每個節點分配32個進程,共設置861個觀測點。測試了1個節點32個進程到256個節點8 192個進程的不同規模。

Figure 12 Large-scale model for testing圖12 大規模測試模型

參考Dublin Test Model,設計組合體模型如圖12所示。在圖12中,電導率σb為0.001 25 S/m的均勻半空間存在一個埋深500 m的低阻異常組合體,組合體的電導率σ1、σ2及σ3分別為0.02 S/m,0.01 S/m和0.005 S/m,對應塊體的尺寸分別為300 m×400 m×600 m,300 m×400 m×600 m,2000 m×400 m×400 m,發射場源為沿y方向布設,長度100 m,電流大小為2 A,觀測區域位于異常體的正上方,x方向:-2 000 m～2 000 m,y方向:-1 000 m～1 000 m,x和y方向間距100 m,共布設861個觀測點。坐標系的源點O設定在異常組合體在水平面投影的中心點處。

Figure 14 Distribution of imaginary component of Ey圖14 Ey虛部分布

計算結果如圖13和圖14所示,分別展示了Ey的實部和虛部,可以看到異常體上方的電場有明顯的變化,不同頻點對異常體均有所反映。

可擴展性測試結果如表1和圖15所示。可以看到,本文開發的并行程序具有較好的可擴展性,相比1個節點32進程,當測試規模達到256節點8 192進程時,加速比為69.69,并行效率為27.22%。

Table 1 Speedup and parallel efficiency of large-scale model表1 大規模模型的加速比及并行效率

Figure 15 Speedup and parallel efficiency of large-scale model圖15 大規模模型的加速比和并行效率

6 結束語

本文詳細描述了一種頻率域電磁積分方程法大規模數值模擬程序的設計、實現方案和測試結果。通過對程序的驗證和測試可以看出,該程序具有較高的精度和較好的可擴展性,具備在大型超算平臺上大規模運行的能力,可以滿足地電磁學中大地電磁、可控源音頻大地電磁等精細數值模擬的需求。