如何開展“以生為主”的數學教學

于智鋒

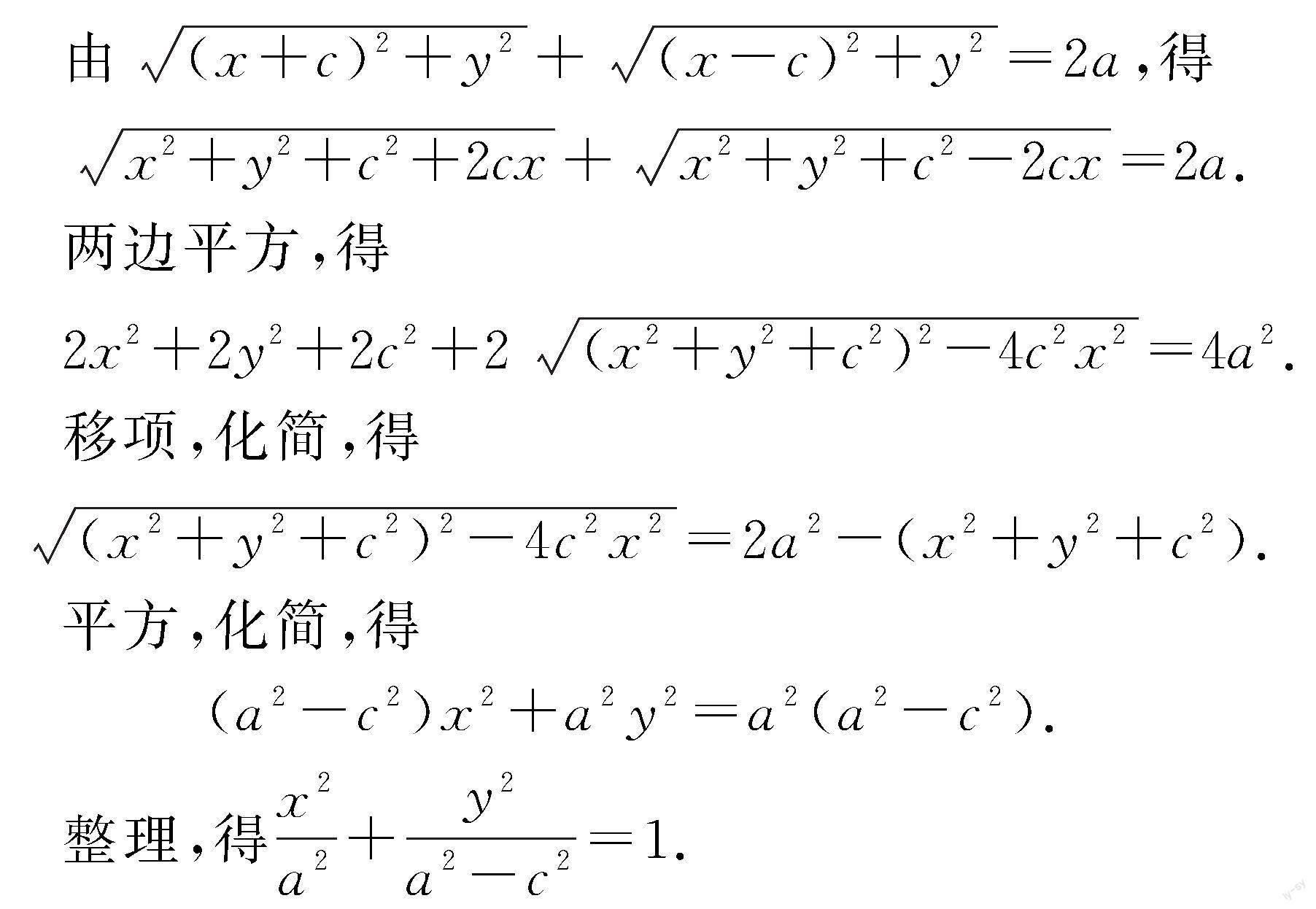
在素質教育的影響下，為了貫徹“因材施教”的教學目標，教師在設計教學方案、實施教學計劃時雖然充分考慮了學生的實際學情，然在具體實施過程中，因受自身教學經驗、解題習慣，以及教學計劃等因素的影響，教師大多會將自己的解題經驗和解題方法以講授的方式傳授給學生，繼而限制了學生個性化思維的培養.同時，為了提升學生的自主學習能力，也會安排學生進行自主學習和合作探究，若在探究時進行過度的引導，就會影響自主學習的效果.其實要認識到，教師的認知水平與學生的認知水平存在較大的差異，切勿將教師的理解、教師的經驗、教師的思維強加于學生的認知水平之上，需多站在學生的角度去思考問題，以學生的認知為出發點，鼓勵學生去嘗試、去實踐，進而真正地做到為“為理解而教”.

1 警惕教師“思維定勢”限制學生發展

眾所周知，在解題教學中若同一問題反復學、重復練，會讓學生產生思維定勢.對于教師亦是如此，很多知識都是反復講、重復教，尤其在新知授課時大多教師已經習慣了固定的模式，即使在開展探究性教學活動時，也會給學生一些暗示，引導學生順著教師的思維去思考和解決問題，這樣往往不利于學生能力的提升，不利于學生個性化發展.

生1：兩邊平方.（學生不假思索地回答.）

師：平方前是否需要將方程變形呢？（筆者試圖打斷學生的思路，按照教材思路求解，避免因繁瑣計算而影響公開課教學效果.）

生1：不需要變形，可以直接平方.（生1執意直接平方.）

師：好的，大家按照生1的思路算一算，看看是否能夠化簡.（讓生1進行板演.）

生1化簡步驟如下：

生1的步驟給出后，在場的教師紛紛點頭稱贊，正是生1的堅持才沒有錯過這樣的精彩.生1的解答值得深思，在教學中是不是將教師的“我認為”強加給了學生呢？在打斷學生之前是否按照學生的思路驗證過呢？其實很多時候教師常常是憑借經驗在教學，認為經常用的、教材或練習冊中給出的就是最優答案.這樣在沒有實踐的情況下就給學生的解題思路做了“此路不通”的預判，顯然很容易限制學生思維的發展，不利于學生思維能力的提升.

2 切勿將教師的“理解”強加給學生

因個體認知結構和思維方式差異的存在，學生的理解能力、分析能力、運算能力也會有所不同，為此在解決同一問題時會涌現出不同解法，也會遇到不同的障礙.那么，為了更好地發展學生，筆者以為，需從尊重學生出發，充分了解學生的思維過程，順著學生的思維去思考，幫助學生掃清思維障礙，切勿將教師認識的“最適合”“最優解”灌輸給學生，那樣不利于學生更好地理解數學，不利于學生解題能力的提升.

3 切勿只重視同化而忽視順應的價值

在數學教學中既要尊重學生，幫助學生完善知識體系建構，發揮同化的作用，同樣也不能忽視順應的價值.當學生的原有認知結構不適合學生發展時，教師需要通過巧妙的引導幫助學生實現認知結構的改組和重建，從而有效地發展學生的認知結構，促進學生能力的提升.

案例3 若cos xcos y+sin xsin y=12，sin 2x+sin 2y=23，則sin（x+y）=[CD#3].

（x+y）－（x－y），再利用兩角和與差的正弦公式展開就可以求解.明明是一道基礎題，平時練習此類問題比比皆是，怎么到考試時還是不會呢？回憶教學過程并結合調研反饋發現，在教學中忽視了學生的困難，也忽視了學生的認知結構，沒有讓學生真正學懂吃透.基于此，針對以上問題借助下列問題進行啟發，引導學生體驗“變角”的價值.

設計意圖：通過方法對比，向學生展示“變角”優勢，讓學生在原有認知的基礎上實現“跳一跳”，發展學生的認知結構.

設計意圖：第一種解法是學生之前的習慣性解法，反映了學生的認知結構；第二種方法是一種新發展.通過方法的對比，體驗不同方法的優缺，進一步體驗“變角”的價值.

通過變式引導學生從角的關系出發，利用角的變化來尋求一個更為自然的解題方式，這樣往往比死記硬背公式更加靈活、高效，同時也可以有效避免遺忘所帶來的困擾，進而使解題更加自然、高效.

總之，教師不要一味地按照自己的思維方式去理解數學、理解學生，應學會換位思考，以“三個理解”為基礎開展有意義的教學，以此提高教師專業素養，提升教學魅力.