“命”核心，“提”素養

謝瑋 王志紅 倪文妍 宋鴻雁

摘要：通過對兩道導數題命制過程的回顧，探析一類導數壓軸試題的命題思路，即從函數f（x）=xex出發，通過求導、變形、引入參數、構造新函數，再通過GeoGebra數形結合控制函數不等式，在此基礎上驗證得到的試題.

關鍵詞：導數；試題命制

1 命題

題目 （原創題）已知函數f（x）=（x－a）ex+2，a∈R.

（1）討論f（x）的單調區間；

2 命題過程

下面我們一起探求上述原創題的命制過程.

如圖1所示：

我們知道，拐點處的切線有其特殊性，它是穿過函數圖象的一條直線.

從不等關系的角度來看，有：

從方程的角度來看，有：

為了使模型簡潔化，我們將函數調整為f（x）=xex+2，此時，它的拐點為（－2，－2），

拐點處的切線方程為y=－x－4.

為了進一步利用上下翻轉的函數圖象變換將不等號統一起來，我們再將函數圖象上平移兩個單位，得到y=xex+2+2，此時，它的拐點為（－2，0），拐點處的切線方程為y=－x－2.

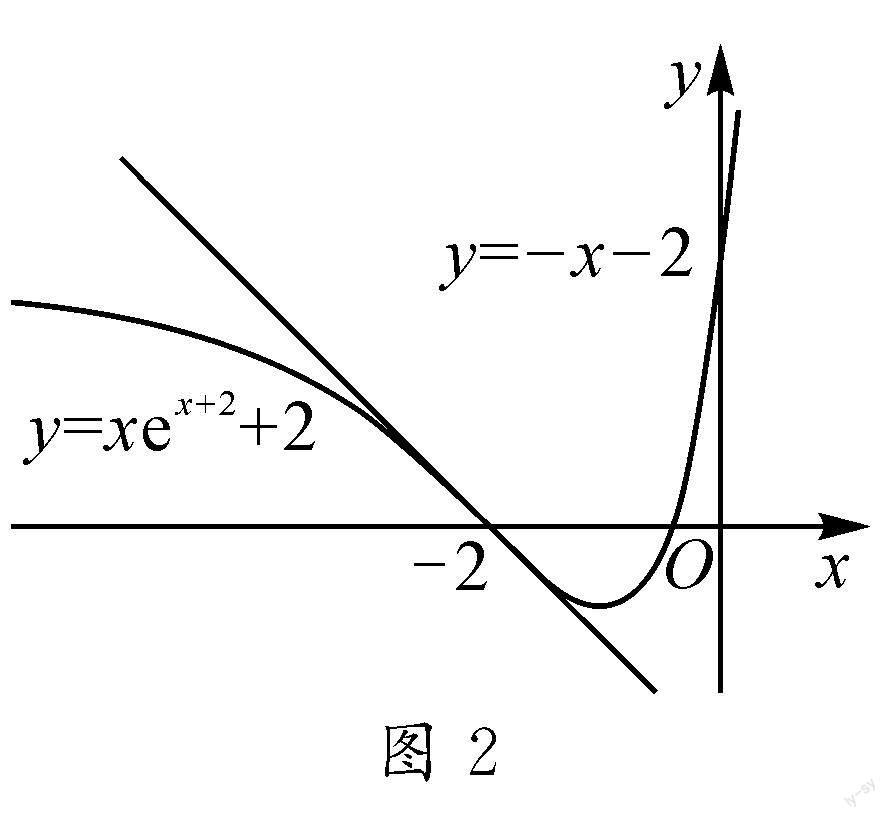
如圖2所示：

從不等關系的角度來看，有：

當x≤－2時，0≤xex+2+2≤－x－2；當x≥－2時，xex+2+2≥－x－2.

從方程的角度來看，有：

對于方程xex+2+2=k（x+2），當k≥0時，有兩個根；－1

至此，我們可以將方程根的個數問題，轉變為函數零點的問題命制一個小題.

題1 若函數f（x）=xex+2－kx－2k+2有三個零點，則實數k的取值范圍是.

再回到不等關系上來，我們知道，絕對值符號可以實現圖象的上下翻轉，從而可以統一不等號的方向，因此構造這樣兩個函數：f（x）=|xex+2+2|，g（x）=|x+2|.兩個函數的圖象如圖3所示.

因此，可以得到這樣一個不等關系：當x≤0時，|xex+2+2|≤|x+2|.

通過這個不等關系，再添加參數可以命制如下一個大題：

題2 已知函數f（x）=xex+2+2，a∈R，

（1）討論f（x）的單調區間；

（2）若x≤0時，|f（x）|≤ax+2，求a的取值范圍.

該問題從本質上來說研究的是曲線與切線的位置關系，由這一方向入手不難想到一個常用的切線放縮模型ln x≤x－1，如果通過合適的圖象變換，可以利用切線放縮將ln x型函數引入到問題中來，也許可以使結構有一定的對稱美.

因此做如下嘗試：

首先將函數f（x）=|xex+2+2|與函數g（x）=x+2的圖象向右平移兩個單位，重新構造函數：f（x）=|（x－2）ex+2|與g（x）=x，使得模型的關鍵點由（－2，0）變為坐標原點. 如圖4所示.

再將對數函數的圖象作適當的平移、翻轉變換，可以得到這樣的結構：

|（x－2）ex+2|≤－ln（－|x|+1），如圖5所示.

然而這一結構過于復雜，且并不具有較好的簡潔性，同時絕對值元素添加較多，與近幾年高考真題結構相去較遠，因此到這里就需要考慮重新調整思路.

讓我們重新回到函數f（x）=xex+2+2，它的拐點為（－2，0），拐點處的切線方程為y=－x－2.前面添加絕對值符號，是為了讓其實現凹凸翻轉，從而統一不等號方向.

當重新思考這個問題的時，我們發現切線的另一含義實際上是泰勒一階展開.從這個角度入手，將函數進行五階泰勒展開，希望從中找到較好的命題入口.

這樣，利用上面得到的恒成立不等關系，添加合適的參數就得到了本文開頭給出的試題.

3 命題小結

本次命題重點對函數曲線在拐點處的切線進行研究，通過相等關系構造函數的零點問題，通過不等關系構造恒成立問題.本題解法靈活多樣，可采用分類討論、分離參數、必要性探路等方法，具體解法再另文刊出.