創設對話情境，實施問題驅動式教學

何勇

摘要：創設合理的對話情境，實施問題驅動式教學，能夠促進學生對數學概念的深度理解，優化學生思維路徑和提出問題、解決問題的方式方法，讓課堂充滿智慧與靈性，彰顯課堂教學的育人價值．

關鍵詞：對話情境；問題驅動；分析問題；解決問題

思維起于問題，起于有問題的情境，發展思維首先要有合適的問題情境.教師要善于創設合適的問題情境，善于發問，善于用問題來激活、驅動和促進學生的思考．近期，在備課組活動中，筆者執教了一節“反比例函數復習”課，通過創設合適的對話情境，用問題驅動的方式把學生的思維引向深入，產生實質性思考，取得了較好的教學效果．下面展示該課的教學預設、生成片斷和教學反思，供大家批評指正．

1 教學預設與課堂生成

1.1 創設數學內部情境，促進概念理解

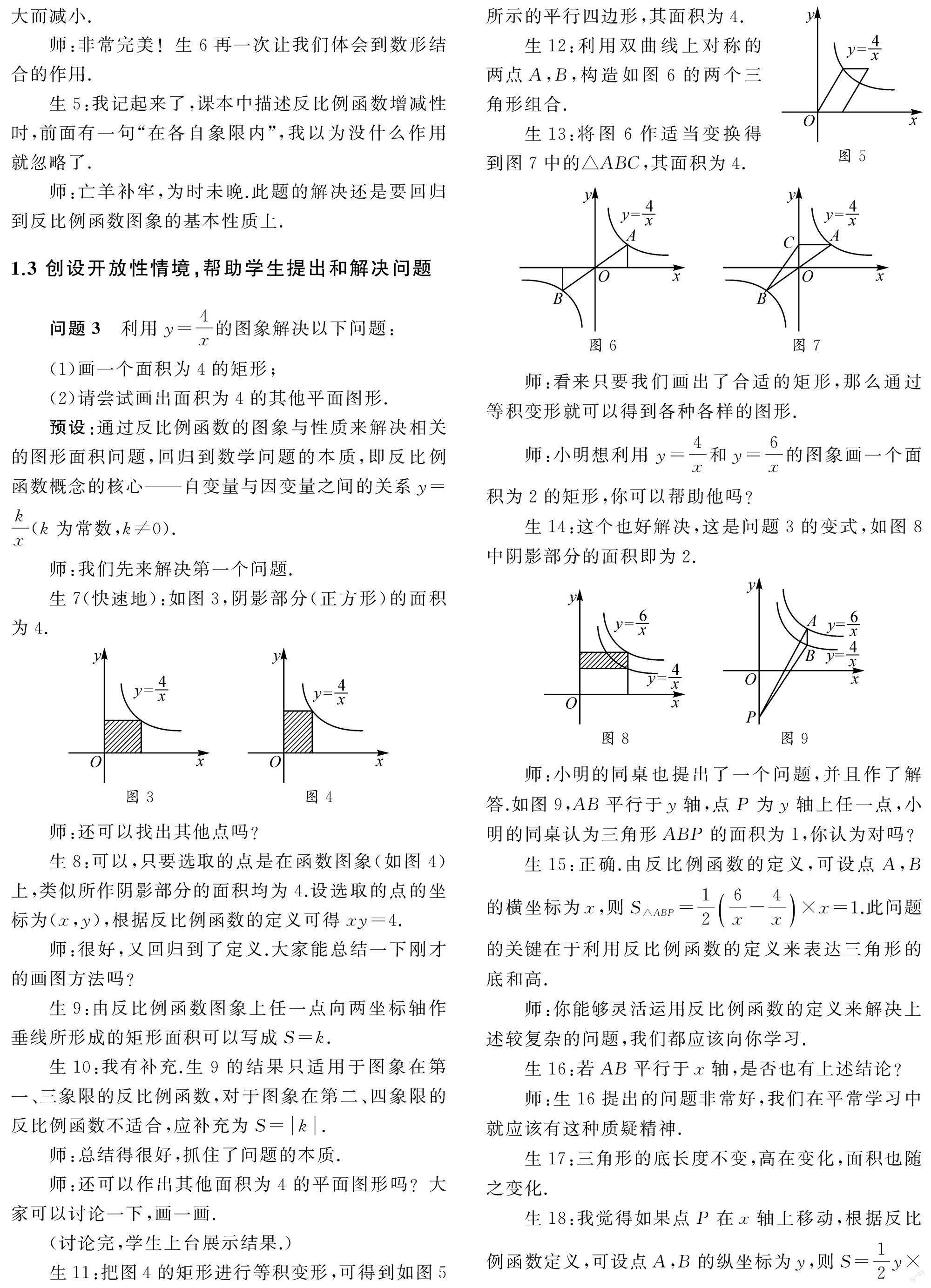
問題1? 已知函數①y=1x+1，②y=1x2，③y=－12x，④y=1x中，y是關于x的反比例函數的有．

預設1：讓學生選擇性判斷幾個形式上類似的關系式，聯想到反比例函數的一般形式，考查學生對反比例函數概念的理解．

預設2：由反比例函數的一般形式過渡到反比例函數的定義，真正了解其變量之間的函數關系．

師：你判斷的依據是什么？

生1：根據反比例函數的定義，把形如y=kx（k為常數，k≠0）的函數稱為反比例函數，所以④為反比例函數．

師：為什么y=1x+1不是反比例函數呢？

生2：從反比例函數的定義來看，y=1x+1不是y關于x的反比例函數，而應該是y關于x＋1的反比例函數．

師：你的回答很到位，真正從數學的本質判斷了此題，謝謝你的精彩分析．

1.2 創設挑戰性情境，優化學生的思維路徑

問題2? 如果反比例函數y=1－3mx的圖象位于第二、四象限，那么m的范圍為．

預設：在得出反比例函數的基本概念后，繼續研究其圖象與性質．

生3：根據反比例函數基本性質可知，圖象位于第二、四象限的反比例函數的比例系數小于0，即1－3m<0，從而得到m>13．

師：若將問題2的條件改為“對于反比例函數y=[SX（]1-3mx[SX）]，若x1

生4：我覺得可以.由“若x1

生5：我同意生4的說法，由圖象增減性遷移到圖象分布的象限，就回到了問題2．

師：兩位同學都依據圖象的增減性，由反比例函數的基本性質推理而得，體現了數學知識的遷移性．

生6：我覺得此題不可以解！

師（追問）：能把你的判斷依據告訴大家嗎？

生6：生5剛才用圖象來解釋，我也用圖象來反駁生5的觀點．如圖2，A（x1，y1），B（x2，y2），滿足的當x1

師：非常完美！生6再一次讓我們體會到數形結合的作用．

生5：我記起來了，課本中描述反比例函數增減性時，前面有一句“在各自象限內”，我以為沒什么作用就忽略了．

師：亡羊補牢，為時未晚.此題的解決還是要回歸到反比例函數圖象的基本性質上．

1.3 創設開放性情境，幫助學生提出和解決問題[BT）]

問題3? 利用y=4x的圖象解決以下問題：

（1）畫一個面積為4的矩形；

（2）請嘗試畫出面積為4的其他平面圖形．

預設：通過反比例函數的圖象與性質來解決相關的圖形面積問題，回歸到數學問題的本質，即反比例函數概念的核心——自變量與因變量之間的關系y=kx（k為常數，k≠0）．

師：我們先來解決第一個問題．

生7（快速地）：如圖3，陰影部分（正方形）的面積為4．

師：還可以找出其他點嗎？

生8：可以，只要選取的點是在函數圖象（如圖4）上，類似所作陰影部分的面積均為4.設選取的點的坐標為（x，y），根據反比例函數的定義可得xy=4．

師：很好，又回歸到了定義．大家能總結一下剛才的畫圖方法嗎？

生9：由反比例函數圖象上任一點向兩坐標軸作垂線所形成的矩形面積可以寫成S=k．

生10：我有補充.生9的結果只適用于圖象在第一、三象限的反比例函數，對于圖象在第二、四象限的反比例函數不適合，應補充為S=k．

師：總結得很好，抓住了問題的本質．

師：還可以作出其他面積為4的平面圖形嗎？大家可以討論一下，畫一畫．

（討論完，學生上臺展示結果.）

生11：把圖4的矩形進行等積變形，可得到如圖5所示的平行四邊形，其面積為4.

生12：利用雙曲線上對稱的兩點A，B，構造如圖6的兩個三角形組合．

生13：將圖6作適當變換得到圖7中的△ABC，其面積為4．

師：看來只要我們畫出了合適的矩形，那么通過等積變形就可以得到各種各樣的圖形．

師：小明想利用y=4x和y=6x的圖象畫一個面積為2的矩形，你可以幫助他嗎？

生14：這個也好解決，這是問題3的變式，如圖8中陰影部分的面積即為2．

師：小明的同桌也提出了一個問題，并且作了解答.如圖9，AB平行于y軸，點P為y軸上任一點，小明的同桌認為三角形ABP的面積為1，你認為對嗎？

生15：正確．由反比例函數的定義，可設點A，B的橫坐標為x，則S△ABP=126x－4x×x=1．

此問題的關鍵在于利用反比例函數的定義來表達三角形的底和高．

師：你能夠靈活運用反比例函數的定義來解決上述較復雜的問題，我們都應該向你學習．

生16：若AB平行于x軸，是否也有上述結論？

師：生16提出的問題非常好，我們在平常學習中就應該有這種質疑精神．

生17：三角形的底長度不變，高在變化，面積也隨之變化．

生18：我覺得如果點P在x軸上移動，根據反比例函數定義，可設點A，B的縱坐標為y，則S=12y×6y－4y=1．

2 教學思考

2.1 對話教學應該成為復習課的一種追求

張增田博士說：“對話教學是指師生在民主、平等、尊重、寬容和愛的氛圍中，以言語、理解、體驗、反思等互動方式，在經驗共享中創生知識和人生價值的教學形態．”由于復習課內容的特殊性，教師更容易采用傳統的“講授式教學”模式，在這種模式下，師生之間難以在課堂上展開真正的對話．因此，教師需要嘗試改變自己的角色，主動營造師生對話的環境，與學生展開平等的對話和交流，這樣學生才愿意在課堂上主動參與教學活動，把握學習的自主權，從而提高學習的能力和效率．

2.2 [JP3]創設豐富的情境素材，使學生能提出數學問題

復習課可看作是由多個“對話模塊”組成的有機整體，而在每一個“對話模塊”中，師生是學習和研究的共同體，雙方一起參與分析、分解、探究等活動．教師在備課時不僅要研究教材，而且要思考“在哪樣的情境中展開對話”“哪類問題可引起學生對已學內容的關注”“提問時采用哪種方式更容易激起學生的思考”等．另外，從一個“對話模塊”向另一個“對話模塊”轉換時，要做到銜接自然、便捷.應在基本知識之間巧妙地設計“對話”情境，找準“最近發展區”，讓學生找到已學知識之間的聯系，幫助他們構建知識網絡，為每個學生提供足夠的探索、研究和發展空間，使每個學生都能進行“再發現”．

2.3 數學情境的設計，要順其自然、追求自然

現代建構主義認為：學習本質上是學習者以已有經驗為基礎，通過與環境的相互作用而主動構建新的理解、新的心理表征的過程．創設數學問題情境正是為了讓學生在原有認知基礎、在與情境的交互作用中主動進行有意義的建構．因此，數學教學應該從數學知識結構和學生的認知結構出發進行設計和組織，以完善和發展原有的認知結構為目標，從數學知識的邏輯發展中提出問題，設計合乎學生認知規律和心理年齡特征的問題情境．這樣才能在自然、合理的情境中幫助學生自然、合理地提出問題、解決問題，在潛移默化中優化學生的思維品質．