立足教材 基于整體 一題串知 上好復習課
陳香屹


新授課像“栽活一棵樹”,復習課似“育好一片林”.栽活一棵樹容易,育好一片林要下功夫.復習課是一種非常重要的課型,對夯實學生的基礎、培養和提高學生運用知識與解決問題的能力起著舉足輕重的作用.怎樣上好復習課?立足教材,一題串知,基于整體,以問題為載體,進行從點到線、由線及面的總結,做到以一點或一題串一線、聯一片,進行知識間縱橫向聯系和比較,構建知識網絡.下面以人教版八年級上冊第15章“分式”章節復習為例,談談本節課的設計思路和意圖.
1 教學環節設計
為了達到“復習整理本章知識結構,形成知識體系,構建知識網絡,解決生活中的實際問題;掌握列分式方程解決實際問題的基本方法,深化數學建模思想的認識”的目標,設計了“創設情境、喚醒舊知—知識梳理、構建體系—范例解析、拓展延伸—課堂小結、深化理解—達標檢測、鞏固提升”五個教學環節開展教學.
1.1 創設情境、喚醒舊知
先播放一段最美鄉村建設中,讓人流連忘返的水上樂園快艇視頻,從而引入數學問題:
一艘游艇在靜水中的最大航速是30 km/h,河水的流速為v km/h.
(1)游艇順水航行的速度是km/h,逆水航行的速度是km/h;
(2)順水航行s km的時間t1是h,逆水航行s km的時間t2是h;
(3)t2比t1多h,t2是t1的倍;
(4)它以最大航速沿河順流航行90 km所用時間,與以最大航速逆流航行60 km所用時間相等,列出的方程是.
設計意圖:教材是教學之本,課堂教學應該立足于教材.教師應該深入地研究教材、吃透教材,從而“創造性”地使用教材.研讀教材中本章主題圖,理解教材的編寫意圖.筆者所選用的問題就是本章教材章引言中的問題,教材中僅有問題(1)和(4),而根據復習的需要,立足教材,設置了問題(2)和(3).聯系實際,在列式中建立解決實際問題的兩個數學模型——分式、分式方程,并為梳理知識作鋪墊.
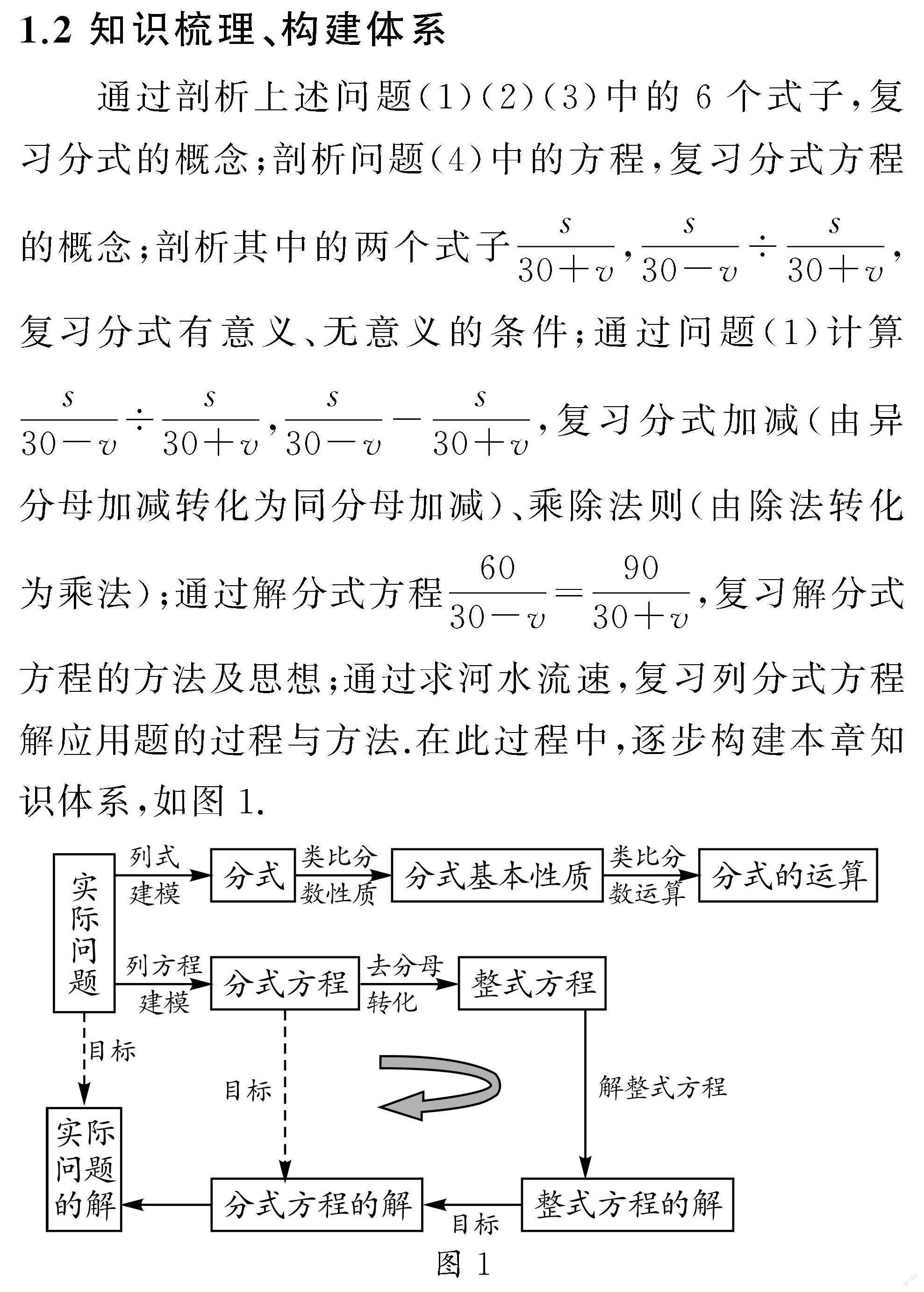
1.2 知識梳理、構建體系
通過剖析上述問題(1)(2)(3)中的6個式子,復習分式的概念;剖析問題(4)中的方程,復習分式方程的概念;剖析其中的兩個式子s30+v,s30-v÷s30+v,復習分式有意義、無意義的條件;通過問題(1)計算s30-v÷s30+v,s30-v-s30+v,復習分式加減(由異分母加減轉化為同分母加減)、乘除法則(由除法轉化為乘法);通過解分式方程6030-v=9030+v,復習解分式方程的方法及思想;通過求河水流速,復習列分式方程解應用題的過程與方法.在此過程中,逐步構建本章知識體系,如圖1.
設計意圖:在復習過程中,需要依據基礎知識的相互聯系及相互轉化關系,對數學知識加以系統整理,梳理歸類,分塊整理,重新組織,形成系統的條理化的知識網絡,使學生所學的知識系統化.在此過程中,要充分發揮學生的自主性,讓學生積極、主動參與歸納、整理的全過程,體現知識讓學生自己梳理,規律讓學生自己尋找,錯誤讓學生自己判斷.因此,本環節按照概念—性質—運算—運用這條主線,圍繞上述四個問題對所學知識進行梳理、總結、歸納,幫助學生理清知識線,建立本章知識結構,形成知識體系.
1.3 范例解析、拓展延伸
設計兩個例題:
例1? 化簡xx-1÷x2+2x+1x2-1.
變式1? 計算xx-1-1÷x2+2x+1x2-1,其中x=14.
變式2? 對于x2+2x+1x2-1÷x-1x+1-x+1,請從-3<x<2的范圍內選取一個合適的整數代入求值.
變式3? 計算xx-1-1÷x2+2x+1x2-1\51x-2,其中x2-x-3=0.
例2? 陳家灣村在水上樂園項目建設中,需新修河堤,現有甲、乙兩個工程隊計劃參與此項工程建設,甲工程隊單獨施工30天完成該工程的13,這時乙工程隊加入,兩隊還需同時施工15天才能完成該項工程,(1)若乙隊單獨施工,需要多少天才能完成該項工程?(2)若甲隊參與該項工程施工的時間不超過36天,則乙隊至少施工多少天才能完成該項工程?
設計意圖:本環節充分體現“有講有練,精講精練,講練結合,以練為主的”原則,通過例題訓練,進一步鞏固分式的計算.被除式不變,除式由單項式變成多項式,計算時既可以把后面的多項式分開看成兩個單項式通分,又可以看成是一個整體進行通分.通過添加一個條件,又融入了整體思想.交換除式和被除式的位置,表面上看方法沒變,但除法運算稍微掌握不好的學生就容易犯錯,用除法的分配律進行計算有效地考查了學生分式的運算技能.例1的每個變式給出字母值的方式也不同——先是具體的一個數,接著是一個范圍,選一個你喜歡的值代入.從具體到抽象,從封閉到開放,從直接到間接,全方位地考查了學生根據分式有無意義求字母值的基本知識.
1.4 課堂小結、深化理解
首先學生自己從知識、能力等方面進行總結,然后教師引導,將本章主要內容歸納概括為:一種運算——分式運算;兩種解題模型——分式、分式方程;三種數學思想——方程思想、類比思想、轉化思想.
設計意圖:培養學生歸納概括能力,從整體上再次認知本章所蘊含的數學知識、思想方法、數學模型,將數學學習提升一個高度,從碎片化到結構化,提高“數學抽象”素養.
1.5 達標檢測、鞏固提升
給出如下達標檢測題:
(1)若分式x2-9x-3的值為0,則x的值為.
(2)據考證,單個雪花的質量約為0.000 25 g,用科學記數法表示為.
(3)關于x的分式方程k-1x+1=2的解為負數,則k的取值范圍為.
(4)計算:x-yx+3y÷x2-y2x2+6xy+9y2-2yx+y.
(5)解方程:xx+1=2x3x+3+1.
設計意圖:對復習的效果進行檢測、評價與反饋,鞏固基礎知識,形成基本技能.
2 教學反思
2.1 立足教材固基礎
教材是按照教學大綱編寫的,是教師傳授知識的主要依據,是學生獲得知識、掌握技能的主要源泉之一.本節課的設計以課本為主,充分挖掘和利用教材,把課本與其他資源有機地結合起來,使之互為補充,相得益彰.
2.2 變式訓練習方法
通過例題的變式,循序漸進,由淺入深,由簡到繁,挖掘分式計算的深度和廣度,突破計算中的難點,達到做一題、學一法、會一類、通一片的能力,舉一反三,歸類變式,從而有效促使學生的思維向多層次、多方向發散,幫助學生在問題的解答過程中去尋找解類似問題的思路、方法,培養學生獨立分析和解決問題的能力.學生通過教師講、自己練,以題歸法、用法解題、題法相融,有常學常新之感,真正達到溫故而知新的效果.
2.3 基于整體提素養
這節復習課有機滲透了單元整體教學思想,通過對一個典型問題進行深入研究,挖掘內在的學習線索與數學本質,科學合理地組織學生開展數學學習活動,從而對所學的知識進行梳理、總結、歸納,幫助學生理清知識線索,建立本章知識結構,形成知識體系,讓本章知識從碎片化到結構化、條理化、系統化,提高數學抽象素養.

