基于作戰(zhàn)交互網(wǎng)絡(luò)的體系作戰(zhàn)能力計算

陳文鈺, 李為民, 張濤, 邵雷, 徐海洋, 王希

(1.空軍工程大學(xué) 研究生院, 陜西 西安 710051; 2.空軍工程大學(xué) 防空反導(dǎo)學(xué)院, 陜西 西安 710051;3.94907部隊, 江西 南昌 330001; 4.31511部隊, 北京 100043; 5.西安衛(wèi)星測控中心, 陜西 西安 710000)

0 引言

隨著信息化、智能化要素的融合發(fā)展,各種新式作戰(zhàn)概念不斷涌現(xiàn),新質(zhì)作戰(zhàn)力量不斷融入作戰(zhàn)體系,體系作戰(zhàn)能力的影響要素越來越繁多,交互關(guān)系越來越耦合與復(fù)雜,對體系作戰(zhàn)能力開展分析也越來越困難。戰(zhàn)爭是不確定性的王國,通過定量化手段分析戰(zhàn)爭規(guī)律是一個艱巨的難題。分析作戰(zhàn)要素及其交互關(guān)系對體系作戰(zhàn)能力和作戰(zhàn)效能的影響,將有助于窺探戰(zhàn)爭迷霧,為現(xiàn)代戰(zhàn)爭制勝機理研究提供依據(jù)。

為對交戰(zhàn)雙方兵力動態(tài)變化開展量化分析,英國工程師Lanchester建立了相應(yīng)的數(shù)學(xué)模型[1-3],揭示了交戰(zhàn)過程中雙方戰(zhàn)斗單位數(shù)量變化對戰(zhàn)爭結(jié)局影響的定量關(guān)系。隨著信息化、智能化時代的來臨,在聯(lián)合全域作戰(zhàn)背景下,各類作戰(zhàn)要素跨域聯(lián)動、即時聚優(yōu)、多域疊加融合,影響體系作戰(zhàn)效能的因素遠不止參戰(zhàn)人數(shù)和武器裝備的火力效能。作戰(zhàn)體系的非線性、涌現(xiàn)、體系崩塌等復(fù)雜性特征明顯,越來越多的學(xué)者認識到作戰(zhàn)體系是開放的復(fù)雜巨系統(tǒng),其復(fù)雜性也是開展體系作戰(zhàn)能力分析的難點。

基于復(fù)雜網(wǎng)絡(luò)理論開展作戰(zhàn)體系分析,是指通過對作戰(zhàn)體系實體的合理抽象,與復(fù)雜網(wǎng)絡(luò)的節(jié)點和邊相互映射,其中各類作戰(zhàn)實體抽象成為復(fù)雜網(wǎng)絡(luò)的節(jié)點,實體之間在作戰(zhàn)中的交互關(guān)系抽象為復(fù)雜網(wǎng)絡(luò)的邊,根據(jù)復(fù)雜網(wǎng)絡(luò)的拓撲結(jié)構(gòu)和網(wǎng)絡(luò)特征開展作戰(zhàn)體系評估,可有效反映體系的非線性、涌現(xiàn)性、級聯(lián)性等特征,是一種行之有效的方法,已受到眾多學(xué)者關(guān)注研究。

基于復(fù)雜網(wǎng)絡(luò)開展作戰(zhàn)體系的研究主要集中于體系結(jié)構(gòu)抗毀性分析[4-8]、體系節(jié)點重要度評估[9-11]、體系貢獻率評估[12-13]、體系作戰(zhàn)能力評估[14]等方面。上述方法的一般性思路是構(gòu)建起作戰(zhàn)體系的網(wǎng)絡(luò)模型,基于針對敵方可形成的作戰(zhàn)回路數(shù)目、有向連通度等指標(biāo)開展分析,取得了一些研究成果。為分析體系的抗毀性,在描述體系受攻擊的場景時,常選用不完全信息下隨機刪除節(jié)點或者完全信息下重要節(jié)點刪除策略。已有的研究中普遍存在以下問題需要改進:

1)網(wǎng)絡(luò)模型的構(gòu)建對于作戰(zhàn)雙方的對抗性表述不足。主要表現(xiàn)在只建立一方的作戰(zhàn)網(wǎng)絡(luò)模型,對于戰(zhàn)爭雙方的交互行為表現(xiàn)不足,對戰(zhàn)爭雙方的毀傷效果未能全面描述,對比時僅以體系自身開展縱向?qū)Ρ?沒有針對敵對雙方交互效果橫向?qū)Ρ确治觥Ｎ墨I[4-5]等雖然構(gòu)建起了作戰(zhàn)體系的網(wǎng)絡(luò)模型,但主要從己方視角開展建模,將敵方節(jié)點忽略作戰(zhàn)性質(zhì)后統(tǒng)一歸類為目標(biāo)類節(jié)點,這導(dǎo)致模型僅能描述一方的體系特性,無法表述雙方的交互作用、作戰(zhàn)雙方的對抗性和作戰(zhàn)能力的。

2)現(xiàn)有的節(jié)點刪除策略與作戰(zhàn)中的攻擊策略相差較大。實驗中,往往需通過刪除節(jié)點來模擬敵方攻擊,分析體系遭受攻擊時的特征規(guī)律?，F(xiàn)有研究中對節(jié)點刪除策略主要有隨機攻擊和優(yōu)先攻擊 2種,涉及的代表文獻有文獻[6-7]和文獻[15]等。

隨機攻擊指忽略節(jié)點特性,對所有節(jié)點隨機刪除,優(yōu)先攻擊是指基于復(fù)雜網(wǎng)絡(luò)的統(tǒng)計特征,按節(jié)點的度、介數(shù)、平均路徑進行先后排序進行攻擊。實際作戰(zhàn)中,對敵方節(jié)點攻擊時不可能采用隨機攻擊的方式。另外,按照敵方節(jié)點重要度開展攻擊的方式要建立在全面掌握對敵方節(jié)點及交互關(guān)系的基礎(chǔ)上,實現(xiàn)起來也不現(xiàn)實。實際中,某一方傾向于攻擊在實際打擊能力范圍內(nèi)的敵方節(jié)點。基于此,本文對節(jié)點的刪除策略展開研究,提出一種可達性節(jié)點攻擊策略,讓體系根據(jù)其預(yù)警偵察情況,根據(jù)所探明的敵方節(jié)點以及自身殺傷鏈實際,對在己方殺傷鏈覆蓋范圍內(nèi)的敵方節(jié)點開展攻擊。為了體現(xiàn)這種關(guān)系,本文基于所提動態(tài)交互網(wǎng)絡(luò)模型,利用己方對敵方節(jié)點殺傷鏈能力和敵方節(jié)點防御能力,建立了節(jié)點刪除策略。

3)現(xiàn)有的研究中過度重視體系可形成殺傷鏈或作戰(zhàn)環(huán)的數(shù)目,認為數(shù)目較大時體系的冗余度會上升,自身抗毀性和對敵作戰(zhàn)能力也會上升,采用這種計算方式有許多不合理之處,例如:殺傷鏈數(shù)目多并不等價于對敵方體系節(jié)點的殺傷范圍廣,若體系內(nèi)形成的殺傷鏈僅僅針對敵方體系內(nèi)的少數(shù)節(jié)點,則即使這樣的殺傷鏈數(shù)目很多,對敵方作戰(zhàn)體系可形成的毀傷規(guī)模也是有限的。另外,若某一節(jié)點存在于多條殺傷鏈中,則該節(jié)點被攻擊時將導(dǎo)致多條殺傷鏈斷鏈?？梢姴荒芡耆詺湐?shù)目衡量體系的作戰(zhàn)能力,體系作戰(zhàn)能力要綜合考慮與節(jié)點自身能力、節(jié)點可靠度、對敵方體系可形成的毀傷規(guī)模等因素有關(guān)。

本文針對復(fù)雜網(wǎng)絡(luò)理論開展作戰(zhàn)體系分析時的上述突出問題,構(gòu)建了一種交互對抗的作戰(zhàn)網(wǎng)絡(luò)模型,建立了節(jié)點能力模型,提出一種基于體系殺傷鏈能力的體系作戰(zhàn)能力求解方法。同時構(gòu)建了節(jié)點防御能力模型,通過設(shè)定的作戰(zhàn)交互規(guī)則實現(xiàn)紅藍體系的作戰(zhàn)交互,通過可形成的殺傷鏈能力與目標(biāo)節(jié)點的防御能力為判斷依據(jù)確定節(jié)點刪除策略,分析了不同類型作戰(zhàn)節(jié)點對體系作戰(zhàn)能力和作戰(zhàn)效能的影響程度。最后仿真驗證了本文模型及方法的有效性。

1 交互作戰(zhàn)網(wǎng)絡(luò)模型的構(gòu)建與描述

1.1 交互網(wǎng)絡(luò)模型構(gòu)建

按照作戰(zhàn)要素的功能屬性,將體系中每個作戰(zhàn)要素抽象為網(wǎng)絡(luò)節(jié)點,要素間的交互關(guān)系可以抽象為網(wǎng)絡(luò)的邊。可以分為以下3類[16]:

1)偵察類節(jié)點(S),主要擔(dān)負對敵方目標(biāo)進行預(yù)警探測、偵察監(jiān)視等任務(wù)作戰(zhàn)要素;

2)指控類節(jié)點(D),主要對源自己方偵察節(jié)點的戰(zhàn)場信息進行分析處理、決策分析、下發(fā)作戰(zhàn)命令的作戰(zhàn)要素;

3)效應(yīng)類節(jié)點(I),主要是指對敵方目標(biāo)實施火力打擊、電子干擾等任務(wù)的作戰(zhàn)要素。

體系的節(jié)點集可以由式(1)表示:

V=VR∪VB

(1)

式中:VR={VRS∪VRD∪VRI}表示紅方節(jié)點結(jié)合;VB={VBS∪VBD∪VBI}表示藍方節(jié)點集合;|V|=|VRS|+|VRD|+|VRI|+|VBS|+|VBD|為作戰(zhàn)體系節(jié)點總數(shù),|Vtype|為type類節(jié)點數(shù)量。

節(jié)點之間存在多種連接關(guān)系,是執(zhí)行各種作戰(zhàn)任務(wù)的基礎(chǔ)。結(jié)合作戰(zhàn)背景,將節(jié)點之間的連接關(guān)系確定16種連接關(guān)系,對應(yīng)網(wǎng)絡(luò)中的16種有向邊,詳細含義如表1所示。

表1 節(jié)點連接關(guān)系Table 1 Factors in the table

集合E={E1∪E2∪…∪Er∪…∪E16}表示網(wǎng)絡(luò)的邊集合,Er代表由第r種交互關(guān)系構(gòu)成的邊集,r=1,2,…,16,type1,type2∈{RS,BD,RI,BS,BD,BI}。

綜上,體系的網(wǎng)絡(luò)模型可由式(2)表示:

G=(V,E)

(2)

1.2 節(jié)點能力模型

能力表示節(jié)點完成任務(wù)的本領(lǐng),節(jié)點能力是一個較為抽象的概念,本文從節(jié)點的可靠度、功能能力和防護能力來對其進行描述?？煽慷仁侵赶到y(tǒng)(或設(shè)備、產(chǎn)品)在規(guī)定的條件下和規(guī)定的時間內(nèi)完成規(guī)定功能的概率[17]。節(jié)點的可靠度為作戰(zhàn)節(jié)點在交戰(zhàn)過程中保證其功能屬性(偵察預(yù)警、指揮控制、效應(yīng)施加)正常發(fā)揮的可靠程度。

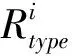
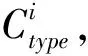
主動交互是指在交互過程中起到主導(dǎo)作用,如E2:BI→RS與E14:BI→RS,雖然節(jié)點類型相同,但是E2連邊表示預(yù)警偵察關(guān)系,其中RS類型的節(jié)點起到主導(dǎo)作用,而E14連邊表示效應(yīng)施加關(guān)系,起主導(dǎo)作用的是BI類型節(jié)點。在本文背景中按照節(jié)點屬性對應(yīng)的功能能力可分別表述為預(yù)警偵察能力、情報上傳能力、效果施加能力。例如,某個預(yù)警偵察節(jié)點與其他節(jié)點發(fā)生主動交互時,若該節(jié)點與其他節(jié)點發(fā)生主動交互、建立有向邊的概率越大,則認為該預(yù)警偵察節(jié)點更容易與其他節(jié)點產(chǎn)生主動交互關(guān)系,其預(yù)警偵察能力越強。

則有

(3)

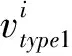
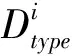
(4)

則有

(5)

G=(V,E)

(6)

式中:

V=VR∪VB

(7)

VR={VRS∪VRD∪VRI}

(8)

VB={VBS∪VBD∪VBI}

(9)

E={E1∪E2∪…∪Er∪…∪E16}

(10)

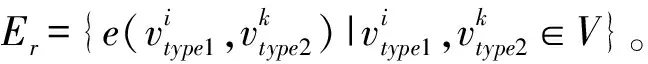
2 基于殺傷鏈能力的體系作戰(zhàn)能力計算

2.1 作戰(zhàn)網(wǎng)絡(luò)殺傷鏈結(jié)構(gòu)模型

殺傷鏈?zhǔn)侵羔槍δ愁惸繕?biāo),各鏈路要素基于預(yù)先規(guī)劃的固定架構(gòu),相互依賴、依序運行,對目標(biāo)產(chǎn)生殺傷效果的任務(wù)環(huán)路閉合模式,殺傷鏈的基本屬性包括閉合性、有序性和依賴性,其核心目標(biāo)是對達成殺傷效果產(chǎn)生效能貢獻[19]。文獻[16]中將包含目標(biāo)節(jié)點的發(fā)現(xiàn)-感知-決策-打擊行動連續(xù)路徑定義為作戰(zhàn)體系網(wǎng)絡(luò)中的殺傷鏈。本文中繼續(xù)沿用其概念內(nèi)涵,將能夠?qū)δ繕?biāo)節(jié)點施加有效效果,由偵察節(jié)點、指控節(jié)點、效應(yīng)節(jié)點依序運行的作戰(zhàn)鏈路稱為殺傷鏈,其組成結(jié)構(gòu)如圖1所示。圖1中紅色箭頭接替形成的閉合鏈條為紅方體系針對藍方目標(biāo)形成的殺傷鏈,藍色箭頭接替形成的閉合鏈條為藍方體系針對紅方目標(biāo)形成的殺傷鏈。

圖1 殺傷鏈?zhǔn)疽鈭DFig.1 Kill chain diagram

要形成對敵方的有效打擊,就要追求殺傷鏈的閉合及快速性,為考慮殺傷鏈的快速性,本文僅考慮最短路徑。以紅方視角為例,最短的殺傷鏈可以由藍方某一節(jié)點作為目標(biāo)節(jié)點、紅方偵察類節(jié)點、紅方指控類節(jié)點、紅方效應(yīng)類節(jié)點組成,所形成的閉合回路中的最短路徑為殺傷鏈。基于上述分析可知,殺傷鏈形成作戰(zhàn)能力的前提是形成完整的OODA閉環(huán),殺傷鏈能力由組成該條殺傷鏈上除目標(biāo)節(jié)點之外的其他節(jié)點功能能力、節(jié)點可靠度決定,本質(zhì)就是殺傷鏈的節(jié)點的不確定性、邊的不確定性因素影響下,殺傷鏈保持正常聯(lián)通的概率。

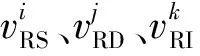
(11)

2.2 體系殺傷鏈能力的數(shù)學(xué)模型

作戰(zhàn)體系中,節(jié)點往往會與其他的多個節(jié)點產(chǎn)生交互,使體系內(nèi)部存在多條針對敵方節(jié)點的殺傷鏈,如圖2所示,表示了針對藍方某個指控節(jié)點形成的兩條殺傷鏈。

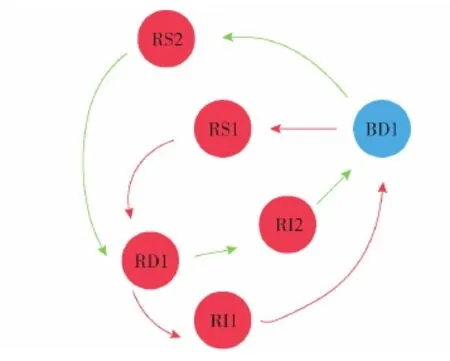
圖2 多條殺傷鏈?zhǔn)疽鈭DFig.2 Multiple kill chains

由此可得:

p={A1∪A2∪…∪An}=p(A1)+p(A2)+…+p(An)- [p(A1A2)+p(A1A3)+…+p(A1An)]+…+

(-1)n-1p(A1A2…An)

(12)

至此,該問題可以轉(zhuǎn)化為2端網(wǎng)絡(luò)聯(lián)通性問題,2端網(wǎng)絡(luò)聯(lián)通性問題是找到源節(jié)點s和終端節(jié)點t之間連接(即存在路徑)的概率,這個問題已經(jīng)在基礎(chǔ)設(shè)施、通信和無線網(wǎng)絡(luò)中得到了廣泛研究[20-24]。

目前存在幾種對網(wǎng)絡(luò)2端聯(lián)通性的精確求解方法[25-27],文獻[28]已經(jīng)證明,精確求解網(wǎng)絡(luò)的2端聯(lián)通性問題屬于NP-hard問題。另外,現(xiàn)有的解析求解方法主要針對等概率網(wǎng)絡(luò),本文網(wǎng)絡(luò)中的節(jié)點間連接概率并不相等,屬于不等概率網(wǎng)絡(luò),解析計算需要更多的計算復(fù)雜度。蒙特卡洛仿真方法的優(yōu)點在于其誤差收斂的速度與問題的規(guī)模、維數(shù)無關(guān),只與仿真次數(shù)有關(guān),因此其時間復(fù)雜度為O(N),N為每次仿真運行的總次數(shù)。為避免網(wǎng)絡(luò)規(guī)模增大帶來的指數(shù)爆炸問題,本文采用蒙特卡洛仿真方法對體系殺傷鏈能力進行求解。

2.3 基于蒙特卡洛仿真的體系殺傷鏈能力求解

蒙特卡洛模擬(MCS)是通過多次實驗求解網(wǎng)絡(luò)兩點的通斷頻率,由柯爾莫哥洛夫強大數(shù)律可知,當(dāng)仿真次數(shù)足夠多時,其通斷頻率可以視為兩點聯(lián)通概率,即求得體系對某一點的打擊能力,可分如下3項內(nèi)容:

1)鄰接矩陣確定。鄰接矩陣可以反映節(jié)點的交互關(guān)系,現(xiàn)有研究往往使用1個鄰接矩陣描述網(wǎng)絡(luò)中所有節(jié)點的關(guān)系,從表1中可以看出,兩種類型的節(jié)點之間也可存在多種交互關(guān)系,如連接E2和E14。因此僅使用1個鄰接矩陣無法全面描述節(jié)點交互關(guān)系。為了合理描述節(jié)點之間的多種交互關(guān)系,本文基于節(jié)點之間的預(yù)警偵察、情報上報、指令下達、效果施加4類關(guān)系,分別建立以下4種作用關(guān)系網(wǎng)絡(luò):

G1=(V,Er),r∈{1,2,3,9,10,11}

(13)

G2=(V,Er),r∈{4,12}

(14)

G3=(V,Er),r∈{5,13}

(15)

G4=(V,Er),r∈{6,7,8,14,15,16}

(16)

G=G1+G2+G3+G4

(17)

式中:G1表示預(yù)警偵察網(wǎng),表示敵我雙方偵察節(jié)點對目標(biāo)節(jié)點的偵察關(guān)系;G2表示情報上報網(wǎng),表示作戰(zhàn)一方內(nèi)部傳感器與指控系統(tǒng)之間的交互關(guān)系;G3表示作戰(zhàn)一方內(nèi)部指控系統(tǒng)與效應(yīng)類節(jié)點(火力打擊節(jié)點、電子對抗節(jié)點等)之間的交互關(guān)系;G4表示一方的效應(yīng)類節(jié)點對另一方目標(biāo)節(jié)點實施效果影響(如火力打擊、電子干擾)的交互關(guān)系。

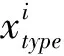
(18)

式中:θk為第k次抽樣隨機值。

(19)

式中:εk為第k次抽樣隨機值。這樣在第k次抽樣中,基于抽樣的隨機值θk、εk和節(jié)點可靠度、節(jié)點功能能力,就能夠確定網(wǎng)絡(luò)中節(jié)點的狀態(tài)與連邊狀態(tài),確定網(wǎng)絡(luò)結(jié)構(gòu),從而得出每個作戰(zhàn)網(wǎng)絡(luò)的鄰接矩陣。

記網(wǎng)絡(luò)Gm的鄰接矩陣為Am(m=1,2,3,4),有

A=A1A2A3A4

(20)

由高次鄰接矩陣法求解有向圖環(huán)數(shù)定理可知,由網(wǎng)絡(luò)G1～G4構(gòu)成的網(wǎng)絡(luò)G中,關(guān)于網(wǎng)絡(luò)中第i個節(jié)點形成的有向環(huán)路數(shù)量為矩陣A的第i行、第i列元素nii。當(dāng)nii≠0時,表示在第k次抽樣中存在對節(jié)點i的殺傷鏈。

3)計算體系對節(jié)點的殺傷鏈能力。若在k次抽樣中針對節(jié)點i存在殺傷鏈的情況出現(xiàn)了次,則得出敵方體系對該節(jié)點的殺傷鏈能力為

(21)

綜合1～3項內(nèi)容描述,構(gòu)建基于蒙特卡洛仿真法求解殺傷鏈能力流程圖,如圖3所示。

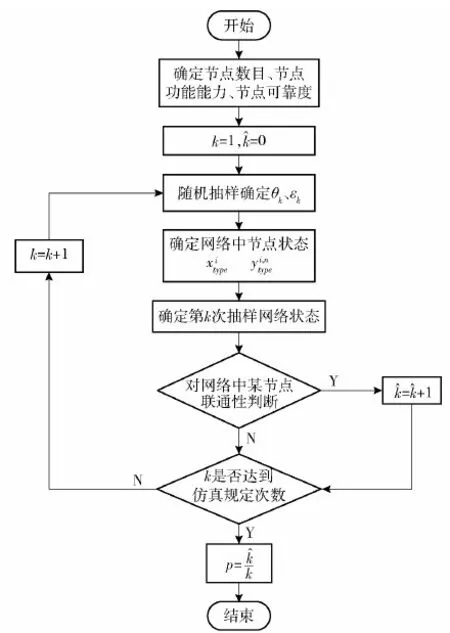
圖3 蒙特卡洛仿真流程Fig.3 Monte Carlo simulation process

2.4 體系作戰(zhàn)能力求解

基于2.3節(jié)思路求解的體系殺傷鏈能力是針對敵方某個節(jié)點的作戰(zhàn)能力。然而,開展作戰(zhàn)體系分析時往往更需要分析對敵方體系整體上可造成的影響。文獻[18]對體系作戰(zhàn)能力定義為:以指揮信息系統(tǒng)為紐帶和支撐,使各種作戰(zhàn)要素、作戰(zhàn)單元、作戰(zhàn)系統(tǒng)相互融合,將實時感知、高效指揮、精確打擊、快速機動、全維防護、綜合保障集成為一體,所形成的具有倍增效應(yīng)的作戰(zhàn)能力。本文考慮建立體系作戰(zhàn)能力模型,實現(xiàn)從整體上對體系作戰(zhàn)能力量化分析。因此,將體系作戰(zhàn)能力的量化為作戰(zhàn)一方可對另一方一定規(guī)模的作戰(zhàn)節(jié)點形成毀傷的概率。以紅方為例,其可對一定規(guī)模的藍方節(jié)點造成毀傷的概率就是體系作戰(zhàn)能力。

若藍方體系有t個節(jié)點,紅方對藍方節(jié)點有效毀傷的概率依次為p1,p2,…,pt,假設(shè)殺傷鏈能力之間相互獨立,則t個節(jié)點中有m個節(jié)點被毀傷的概率Pm為

P0=P{m=0}=(1-p1)(1-p2)…(1-pt)

(22)

P1=P{m=1}=p1(1-p2)…(1-pt)+

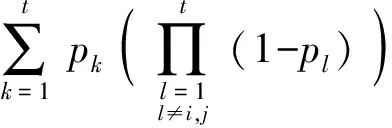
(23)

P2=P{m=2}=p1p2(1-p3)…(1-pt)+p1p3(1-p2)…(1-pt)+…+pt-1pt(1-p1)(1-p2)…(1-pt-1)=

(24)

由此可推導(dǎo)得

(25)

若將一定規(guī)模節(jié)點的毀傷視作至少造成m個節(jié)點毀傷,則體系作戰(zhàn)能力由式(26)表示:

(26)

2.5 網(wǎng)絡(luò)節(jié)點攻擊及更新策略

節(jié)點是承受敵方攻擊的載體,作戰(zhàn)網(wǎng)絡(luò)攻擊主要針對節(jié)點展開。現(xiàn)有研究中節(jié)點的攻擊主要不完全信息下的隨機攻擊策略和基于復(fù)雜網(wǎng)絡(luò)的統(tǒng)計特征,如節(jié)點的度、介數(shù)、平均路徑等完全信息下的優(yōu)先攻擊策略[29]。實際中獲取敵方作戰(zhàn)體系的全部信息以計算其節(jié)點的統(tǒng)計特征,而后采用優(yōu)先攻擊策略的方式不現(xiàn)實,同時對敵方采取隨機攻擊、任意攻擊的策略也不符合軍事常識。因此需要在網(wǎng)絡(luò)交互模型基礎(chǔ)上設(shè)定1種節(jié)點攻擊策略。

本文提出1種可達性攻擊策略,即一方能對另一方體系可形成殺傷鏈能力則視為對敵方節(jié)點具備可達性攻擊水平,可以實施攻擊,以反映現(xiàn)代戰(zhàn)爭發(fā)現(xiàn)即摧毀的特征要求。

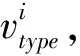
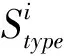
(27)

3 仿真案例分析

3.1 體系作戰(zhàn)能力分析

為分析體系作戰(zhàn)能力,尋找影響體系作戰(zhàn)能力的關(guān)鍵變量,開展如下仿真分析。

假設(shè)初始時刻,紅方擁有10個偵察類節(jié)點、 5個指控類節(jié)點、10個效應(yīng)類節(jié)點,為分別分析體系作戰(zhàn)的影響要素,藍方體系節(jié)點類型和數(shù)量在初始時刻與紅方完全相同,雙方共計50個節(jié)點。

為了分析變量存在差異情況下對作戰(zhàn)雙方造成的影響,除變量外,紅藍雙方節(jié)點功能能力、節(jié)點可靠度、節(jié)點防護能力均相同。設(shè)定節(jié)點功能能力值期望均為0.3,能力值方差為0.01,表示同類型節(jié)點之間的能力差異程度;節(jié)點防護能力值期望均為0.8,防護能力方差為0.01,表示同類型節(jié)點防護能力差異程度;節(jié)點可靠度值期望為0.8,可靠度方差為0.01,表示同類型節(jié)點可靠度差異程度。衡量體系作戰(zhàn)能力時,對敵方節(jié)點毀傷規(guī)模設(shè)定為70%以上的節(jié)點毀傷規(guī)模。

在某一次網(wǎng)絡(luò)抽樣中,根據(jù)紅藍作戰(zhàn)體系的網(wǎng)絡(luò)模型確定網(wǎng)絡(luò)鄰接矩陣,用Gephi軟件做出體系雙方的網(wǎng)絡(luò)拓撲圖如圖4所示。由圖4可以看出,體系中仍然存在一定比例的孤立節(jié)點,但整體來看交互關(guān)系復(fù)雜。

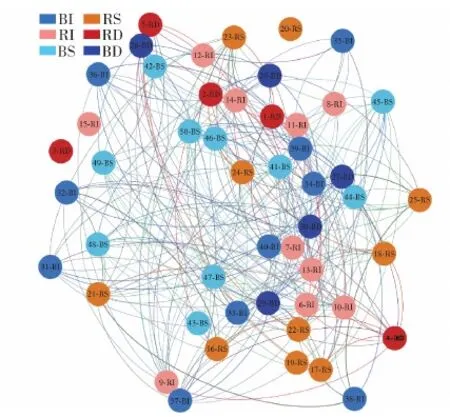
圖4 紅藍作戰(zhàn)體系網(wǎng)絡(luò)拓撲圖Fig.4 Network topology of the Red-Blue Combat System

每類節(jié)點的詳細情況匯總?cè)绫?所示。

以下進行作戰(zhàn)網(wǎng)絡(luò)交互實驗分析。在作戰(zhàn)網(wǎng)絡(luò)交互實驗中,除了開展分析的節(jié)點能力由0.1～1.0依次遞增,保持其他節(jié)點功能能力、可靠度、防護能力按表2中所描述的情況不變,蒙特卡洛仿真次數(shù)設(shè)定為5 000,分別求解作戰(zhàn)交互前紅藍方對敵節(jié)點形成殺傷鏈數(shù)目的平均值、交互前紅藍雙方體系作戰(zhàn)能力。

然后,基于可對敵方形成的殺傷鏈能力,按照3.5節(jié)的節(jié)點更新策略對毀損節(jié)點進行刪除,更新作戰(zhàn)網(wǎng)絡(luò),求解更新后紅藍體系對敵節(jié)點形成殺傷鏈數(shù)目的平均值、紅藍雙方體系作戰(zhàn)能力、對敵方體系造成的實際損毀比例。以紅方視角為例,分別對RD、RI、RS的功能能力依次由0.1～1.0變化時對體系交互前后影響進行分析如下,如圖5～圖9所示。

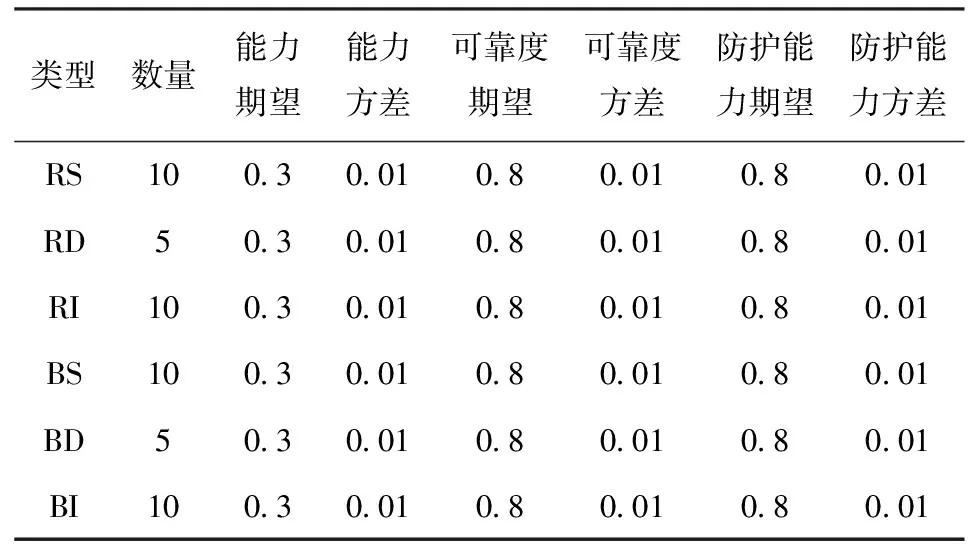
表2 作戰(zhàn)節(jié)點詳細情況Table 2 Detailed data of combat nodes

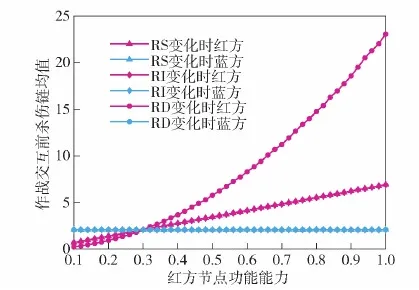
圖5 不同類型紅方節(jié)點的功能能力對交互前殺傷鏈均值的影響Fig.5 Influence of functional ability of different types of red cube nodes on mean value of kill chain before interaction

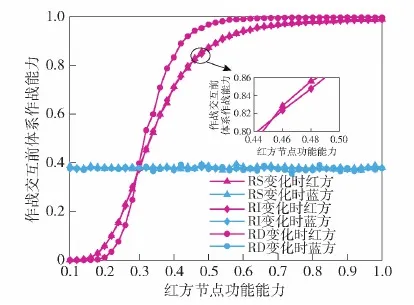
圖6 不同類型紅方節(jié)點的功能能力對交互前體系作戰(zhàn)能力的影響Fig.6 Influence of functional capability of different red cube nodes on combat capability before interaction

從圖5中可以看出:指控類節(jié)點的功能能力從0.1變?yōu)?.0的過程中,其對殺傷鏈數(shù)目增長的影響是非線性的;而效應(yīng)類和偵察類節(jié)點的功能能力提升時,對于殺傷鏈數(shù)目的影響是線性的,且效應(yīng)類、偵察類節(jié)點對殺傷鏈數(shù)目的影響作用相當(dāng)。

圖6表明,當(dāng)紅方指控類節(jié)點的功能能力在0.6左右時,其對藍方體系70%以上節(jié)點造成毀傷的概率趨向于1.0。而紅方偵察類、效應(yīng)類節(jié)點要達到相同程度,必須將節(jié)點的功能能力提升至0.9以上。

圖7中紅方殺傷鏈均值在中途出現(xiàn)中斷情況,結(jié)合圖9,以紅方指控類節(jié)點為例分析,當(dāng)節(jié)點功能能力為0.4以上時,對藍方體系節(jié)點毀傷比例可以達到100%,此時由于再無藍方節(jié)點,缺失目標(biāo)節(jié)點,發(fā)生一次作戰(zhàn)交互后,紅方體系無法形成殺傷鏈,導(dǎo)致殺傷鏈均值出現(xiàn)中斷。

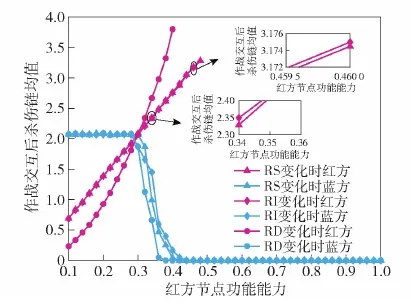
圖7 不同類型紅方節(jié)點的功能能力對交互后殺傷鏈均值的影響Fig.7 Influence of functional ability of different types of red cube nodes on mean value of kill chain after interaction

圖8 不同類型紅方節(jié)點的功能能力對交互后體系作戰(zhàn)能力的影響Fig.8 Influence of functional capability of different red cube nodes on combat capability after interaction

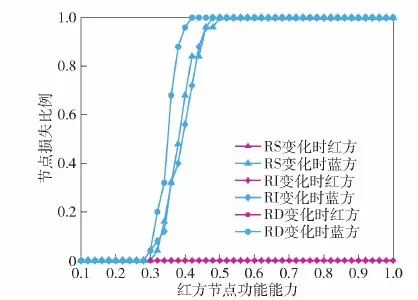
圖9 不同類型紅方節(jié)點的功能能力對交互后 雙方節(jié)點損失比例的影響Fig.9 Influence of functional ability of different types of red cube nodes on the loss ratio of both sides after interaction

在圖8中可以看出,在紅方節(jié)點的功能能力達到0.30～0.35左右時,藍方體系作戰(zhàn)交互后的作戰(zhàn)能力將大幅下降,對紅方70%的節(jié)點造成毀傷的幾率基本為0。

由圖6～圖9可看出,相比偵察類、效應(yīng)類節(jié)點,指控節(jié)點功能能力提升對體系作戰(zhàn)能力提升更加明顯,是作戰(zhàn)體系的核心關(guān)鍵,對己方體系能力的非線性提升、敵方體系作戰(zhàn)能力的非線性壓制具有重要作用。由于藍方節(jié)點功能能力一直未改變,所以藍方交互前殺傷鏈平均數(shù)目、藍方體系作戰(zhàn)能力、紅方節(jié)點損失比例也未變化。

3.2 對比分析及案例應(yīng)用

為驗證本文提出的體系能力計算方法的優(yōu)越性與合理性,本節(jié)通過在實際作戰(zhàn)場景下與文獻[15]方法的對比展開分析驗證。

假設(shè)作戰(zhàn)場景為:某兩個長期相互對峙的A(紅方)與B(藍方),在某次對峙事件中,A在對峙一線共使用預(yù)警衛(wèi)星、雷達等預(yù)警探測類節(jié)點計9個,構(gòu)建3個戰(zhàn)役級指控中心,投入遠程火箭彈、地對空導(dǎo)彈等9個效應(yīng)類節(jié)點。為分析A指控中心的能力提升對作戰(zhàn)能力提升的影響,并考慮到B與A處于均勢對峙的實際,假設(shè)B投入的作戰(zhàn)力量規(guī)模結(jié)構(gòu)與A國相當(dāng)。

所得作戰(zhàn)節(jié)點詳細情況如表3所示。

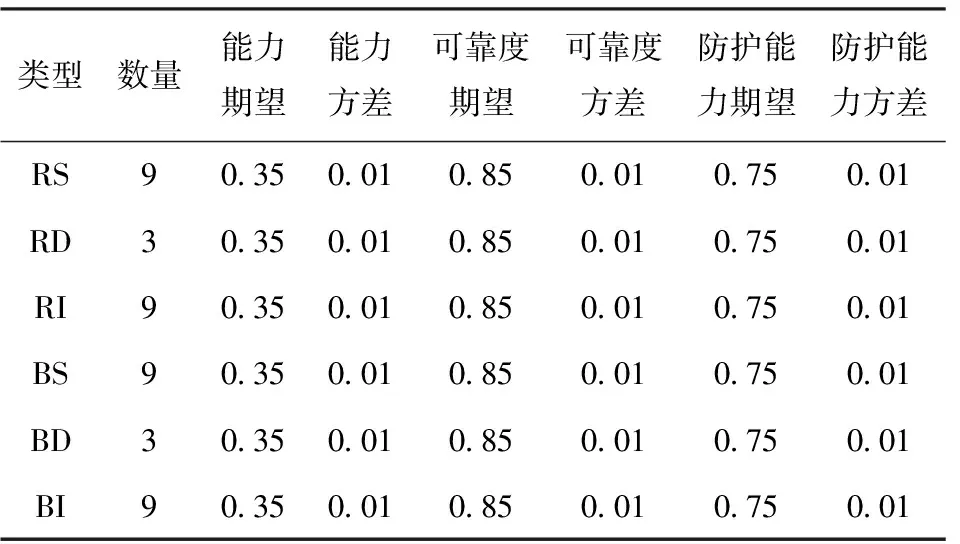
表3 A與B的作戰(zhàn)節(jié)點情況Table 3 Operation nodes of country A and country B

文獻[15]中計算體系作戰(zhàn)能力的主要步驟為:

步驟1對于某殺傷鏈lj,其包含的偵察類節(jié)點的集合為S={sj},決策類節(jié)點的集合為D={dj},效應(yīng)類節(jié)點的集合為I={ij},得到該條殺傷鏈的作戰(zhàn)能力由式(28)表示:

(28)

式中:CAS(sj)、CAD(dj)和CAI(ij)分別為體系中偵察類節(jié)點、決策類節(jié)點和效應(yīng)類節(jié)點具有的能力;|lj|為殺傷鏈lj的長度。

步驟2對于一個作戰(zhàn)體系,若其包含m條殺傷鏈集合LG={lk}k=1,2,3,…,m,則該體系的作戰(zhàn)能力為

(29)

步驟3基于上述數(shù)據(jù),設(shè)定蒙特卡洛仿真次數(shù)設(shè)定為2 000,為保證文獻[15]中結(jié)果的穩(wěn)定性,對其進行1 000次計算求均值。除特殊說明外,其他仿真參數(shù)設(shè)定與3.1節(jié)相同。由于3.1節(jié)中已經(jīng)驗證了所有類型節(jié)點對于作戰(zhàn)效果的影響,本節(jié)主要對比本文方法相對其他文獻方法的優(yōu)點,僅選擇紅方指控類節(jié)點的功能能力變化時對作戰(zhàn)體系及交互效果的影響。

仿真結(jié)果如圖10～圖16所示,其中圖10～圖14是運用本文方法所得的結(jié)果,圖15～圖16是運用文獻[15]中方法所得的結(jié)果。

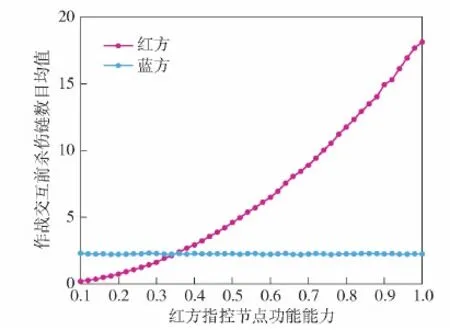
圖10 交互前殺傷鏈數(shù)目均值Fig.10 Mean number of killing chains before interaction

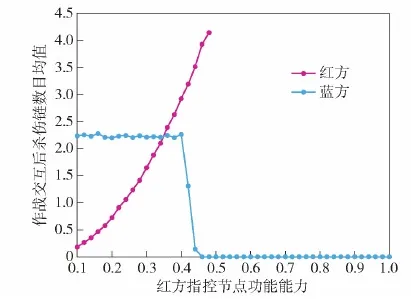
圖11 交互后殺傷鏈數(shù)目均值Fig.11 Average number of kill chains after interaction

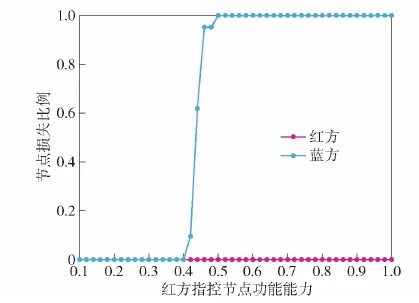
圖12 交互后雙方的節(jié)點損失比例Fig.12 Node loss ratio of both sides after interaction

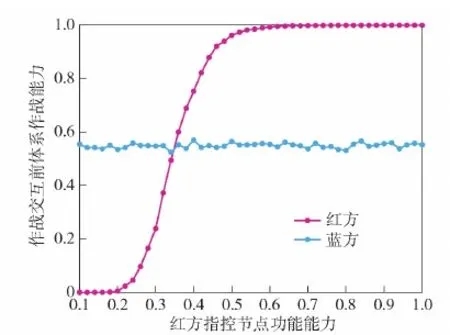
圖13 交互前體系作戰(zhàn)能力Fig.13 System combat capability before interaction

圖15 交互前體系作戰(zhàn)能力(文獻[15]中的方法)Fig.15 System combat capability before interaction (in Ref.[15])

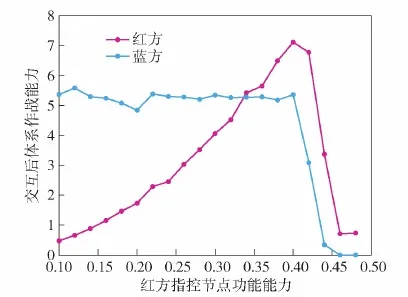
圖16 交互后體系作戰(zhàn)能力(文獻[15]中的方法)Fig.16 System combat capability after interaction (in Ref.[15])

對比圖13和圖15可以看出,藍方的體系作戰(zhàn)能力均保持穩(wěn)定,但紅方指控類節(jié)點功能能力變化時,兩種方法下紅方體系交互前的作戰(zhàn)能力變化趨勢不同。按文獻[15]中的方法,其能力將隨著紅方指控能力的增加而非線性增加,并且增加速度越來越快。本文方法中,紅方體系作戰(zhàn)能力趨于1之后便飽和,意味著指控類節(jié)點的功能能力持續(xù)性增大時,體系能力的提升效果并不一定會相應(yīng)增大,這表明節(jié)點能力需適度增加,過度增加對體系能力提升意義不大,這對適度提升節(jié)點能力、有效提升作戰(zhàn)效能、避免作戰(zhàn)資源浪費具有參考意義;用文獻[15]中的方法,易得出只要無限增大節(jié)點能力,體系能力也會無限增大,不僅與主觀認識不符,也不利于指導(dǎo)開展作戰(zhàn)能力建設(shè)工作。

由圖14可以看出:隨著紅方節(jié)點功能能力增加,交互后的體系作戰(zhàn)能力呈現(xiàn)緩慢增加、快速增加和保持穩(wěn)定3個階段,緩慢增加是由于前期紅方指控節(jié)點能力相比藍方差距較大,節(jié)點能力的提升對作戰(zhàn)交互效果影響不大;但隨著紅方節(jié)點能力提升到與藍方節(jié)點能力水平相當(dāng),紅方作戰(zhàn)交互后的體系能力會進入急速增長期,此時交互后的作戰(zhàn)能力增加較快,并迅速進入飽和階段,同時藍方交互后的作戰(zhàn)能力也迅速下降,體現(xiàn)為能力崩塌效應(yīng),最終,二者交互后的能力趨于穩(wěn)定,意味著紅方取得決定性優(yōu)勢。

同樣對比圖16,可以看出利用文獻[15]中的方法計算交互后體系作戰(zhàn)能力,藍方呈現(xiàn)先平穩(wěn)、后下降的趨勢,最終也趨于0,這與本文方法一致。但是其反映的紅方作戰(zhàn)能力呈現(xiàn)先上升、后下降的反?，F(xiàn)象,究其原因,由于交互后造成了藍方節(jié)點損失,對紅方殺傷鏈可提供目標(biāo)節(jié)點數(shù)量變少,致使紅方殺傷鏈數(shù)目下降,從而造成紅方交互后體系能力下降的反常情況,這顯然與客觀實際不符。

綜上分析,相比文獻[15]中計算體系作戰(zhàn)能力的方法,本文方法不依賴于殺傷鏈的數(shù)目,更加關(guān)注體系作戰(zhàn)的整體性效果,從而實現(xiàn)對作戰(zhàn)能力的科學(xué)評估。

4 結(jié)論

本文通過構(gòu)建交互網(wǎng)絡(luò),建立紅藍交互的網(wǎng)絡(luò)模型,同時提出了殺傷鏈能力、體系殺傷鏈能力、體系作戰(zhàn)能力的數(shù)學(xué)模型,開展了基于復(fù)雜網(wǎng)絡(luò)理論的作戰(zhàn)體系能力分析。

經(jīng)過本文研究,可看出作戰(zhàn)交互的體系作戰(zhàn)能力變化趨勢、不同節(jié)點功能能力對現(xiàn)代作戰(zhàn)體系的重要性,對比研究也顯示了本文方法的科學(xué)性和有效性。本文方法可以為基于復(fù)雜網(wǎng)絡(luò)開展作戰(zhàn)體系能力分析時的網(wǎng)絡(luò)建模、能力分析等研究提供參考借鑒。為了簡化,本文未考慮體系的層級結(jié)構(gòu)和權(quán)重影響,這是下一步的研究方向和重點。