基于偽距離的混凝土泵車臂架避障運動控制研究

黃毅　胡勇　范佳源　胡明　湯麒英　熊英濤

摘要：針對混凝土泵車臂架末端避障和臂架關節限制問題，提出一種基于偽距離的泵車臂架避障方法。運用超二次曲面函數表示空間障礙物，采用偽距離作為臂架與空間障礙物的接近程度指標。基于最小偽距離判別指標，對泵車臂架賦予一個避障速度，并對傳統梯度投影算法進行改進，在避免關節運動超過關節極限位置的情況下實現泵車臂架的安全避障，同時保證避障過程的平穩性和臂架末端的軌跡精度。仿真及半物理實驗驗證了該算法在混凝土泵車臂架避障過程中的有效性，且能完成空間多障礙物避障。

關鍵詞：梯度投影法；關節避障極限；偽距離；避障；冗余度臂架；混凝土泵車

中圖分類號：TH6

DOI：10.3969/j.issn.1004-132X.2023.12.012

Study on Obstacle Avoidance Control of Concrete Pump Truck Booms Based on Pseudo-distance Method

HUANG Yi HU Yong FAN Jiayuan HU Ming TANG Qiying Xiong Yingtao

Abstract： Aiming at the problems of end obstacle avoidance and joint limitation of concrete pump truck boom， an obstacle avoidance method of pump truck boom was proposed based on pseudo-distance. Superquadratic function was used to represent space obstacle， and pseudo-distance was used as the index of proximity between boom and space obstacle. Based on the minimum pseudo-distance discriminant index， an obstacle avoidance speed was assigned to the boom of the pump truck， and the traditional gradient projection algorithm was improved to realize the safe obstacle avoidance of the boom of the pump truck under the condition of avoiding the joint movement exceeding the joint limit position， while ensuring the stability of the obstacle avoidance processes and the trajectory accuracy of the boom end. Simulation and semi-physical experiments verified the effectiveness of the algorithm in concrete pump truck boom obstacle avoidance processes， which may complete the space multi-obstacle avoidances.

Key words： gradient projection method; joint avoidance limit; pseudo-distance; obstacle avoidance; redundant boom； concrete pump truck

0 引言

混凝土泵車是一種通過泵車臂架將混凝土連續均勻地輸送到澆筑點的專用工程機械。隨著對工程機械的要求越來越智能化、無人化，人們不但要求混凝土泵車臂架能夠在施工現場實現自動澆筑，還要求能夠對遇到的障礙物實現自動安全避障［1］。泵車臂架可以看作是一種由液壓驅動的超長冗余度機械臂，冗余度機械臂利用其冗余度的特性可在不影響末端執行任務的前提下完成其他任務，在奇異處理、避障、關節避障極限、提高可操作性等方面具有顯著優勢［2-4］。

避障是冗余度機械臂研究的一個重要內容，冗余度機械臂避障方法主要有基于優化準則的梯度投影法和人工勢場法。此外，根據應用場景的不同避障方法分為離線方法和在線方法［5-6］，離線避障方法是對周圍環境提前進行建模，當周圍環境改變時可能導致避障失敗，因此應用更多的是在線避障方法，根據傳感器獲取的信息實時規劃運動路徑實現在線避障。PERDEREAU等［7］提出了一種冗余度機械臂實時避碰方案，該方案將冗余作為一個無約束優化問題，冗余與路徑跟蹤和避障約束集成到一個增強目標函數中最終實現避障。YOSHIDA等［8］提出了一種基于迭代規劃方案的復雜環境下三維無碰撞運動生成的實用規劃框架。BENZAOUI等［9］利用擴展雅可比矩陣實現了平面三連桿機械臂避障控制。GUAN等［10］提出了一種適用于多移動障礙物的避障算法，基于廣義逆方法將逃逸速度引入其中，得到機械臂的關節速度，從而完成避障軌跡規劃。HU等［11］利用后向二次搜索算法，結合阻尼最小二乘法、加權最小范數法和梯度投影法，對可能發生的從末端到基座的障礙物碰撞進行向后搜索，并成功實現避障。DE等［12］基于人工勢場法中的斥力場提出了Pivot算法，將排斥力作用于機械臂末端，使機械臂末端能夠避開動態障礙物。隨著機械臂的自由度和障礙物數目的增加，獲取機械臂與障礙物之間的最小歐氏距離變得越來越困難，因此，眾多學者對檢測障礙物到機械臂之間的距離檢測也進行了研究。另外，對障礙物進行建模是實時避障的關鍵，為了減小計算量和提高效率，通常使用簡單的幾何單元來表示障礙物。CHEN等［13］對障礙物和冗余機器人連桿用最接近其體積的橢球建模，基于兩者之間的最小距離采用虛擬力進行避障。WANG等［14］基于人工勢場方法，將機器人避障簡化成線段與球之間的避障。ZHAO等［15］提出將超冗余度機械臂和工作空間中的障礙物作為邊界橢圓進行建模，實現了超冗余度機械臂的靈活避障。CHOI等［16］分別用球體和橢球代表障礙物和機械臂，將機械臂與障礙物之間的碰撞距離定義為碰撞度量指標，通過最小化碰撞度量指標來實現避障任務。HWANG等［17］也將工作空間中的障礙物建模為橢球體以簡化數學表示，并減小碰撞檢測的計算復雜度。PATEL等［18］利用對偶向量和角度的概念提出了一種緊湊的圓柱體-圓柱體碰撞檢測和距離計算方法。然而，上述這些方法對障礙物與機械臂之間的最小距離很難獲得精確的解析式。BRICE等［19］運用超曲面對障礙物進行建模，提出了一種冗余度機械臂自適應控制方案。MU等［20-21］將障礙物表面采用超二次曲面函數表示，采用偽距離來評估機械臂與障礙物之間的接近程度，并提出了一種偽距離歸一化處理方法，成功完成了冗余度機械臂的避障任務。

本文針對混凝土泵車臂架末端的避障問題，同時考慮泵車臂架結構的關節極限限制，結合偽距離概念，提出一種基于偽距離的改進梯度投影避障算法。對障礙物表面進行超二次函數表示，采用具有解析式的偽距離來評估臂架與障礙物的接近程度，并對傳統梯度投影法冗余度臂架避障方法進行改進，完成對臂架避障過程中各臂節關節轉角在關節極限位置的限定。基于最小偽距離判別指標對泵車臂架賦予一個避障速度，實現對空間障礙物的避障。以中聯重科38 m混凝土泵車為研究對象，開展混凝土泵車臂架避障運動控制的仿真和半物理實驗，驗證該方法在臂架避障過程中的可行性。

1 泵車臂架避障模型建立及偽距離計算

1.1 泵車臂架系統運動學分析

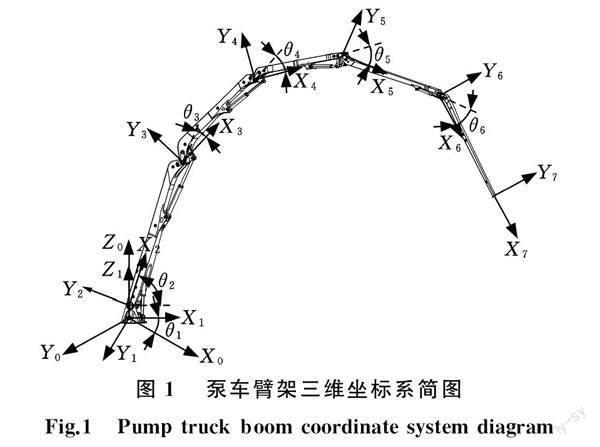
混凝土泵車臂架系統是一種冗余自由度結構系統，五節臂混凝土泵車臂架系統是一個六自由度冗余系統，將泵車臂架系統簡化為一個剛性結構系統，便可以運用機器人學理論進行運動學分析。采用D-H法對泵車臂架系統建立正向運動學方程，其臂架系統簡圖見圖1，D-H參數如表1所示，坐標系定義為：（X0，Y0，Z0）為基坐標系，（Xi，Yi，Zi）為轉臺和各臂架坐標系，X軸方向指向臂架離開的方向。

運用D-H法可求得臂架末端軌跡方程和雅可比矩陣：

2 基于偽距離的泵車臂架避障算法建模

2.1 關節避障極限

由于泵車臂架結構、液壓等因素限制，泵車每節臂架都有運動范圍，存在關節運動極限，無法直接引用傳統梯度投影法。針對這一情況，對傳統梯度投影法冗余度機械臂避障方法進行改進，實現對各臂節關節轉角極限的限定。

3 仿真分析與半物理仿真實驗驗證

3.1 仿真分析

為驗證本文的基于偽距離的混凝土泵車臂架三維避障算法的有效性，以中聯重科38 m混凝土泵車臂架為研究對象，進行本避障算法仿真，仿真環境為MATLAB R2021a，驗證臂架避障運動控制過程中臂架轉角的極限情況和避障效果。

混凝土泵車臂架結構參數分別為： d2=0.77 m，d5=0.48 m，l1=7.136 m， l2=5.479 m， l3=5.21 m， l4=5.466 m， l5=5.32 m。轉臺及各臂架轉動角度范圍為：θ1∈［－π，π］，θ2∈［0，π/2］，θ3∈［－π，0］，θ4∈［－π，0］，θ5∈［－13π/36，π］，θ6∈［－π，π/18］。轉臺及各臂架初始位姿角度為：θ=（0，4π/9，－π/3，－π/6，－π/12，－π/5），對應末端臂架位置為（19.051，-0.48，1.803） m。

設定障礙物R=0.5 m、H=2 m，障礙物中心為（16.5，-0.48，1） m的障礙物，臂架擬合圓柱體半徑r=0.25 m，臂架末端以0.25 m/s的水平速度向左運動，運動中臂架會檢測到障礙物，實時計算末節臂架與障礙物的偽距離，并根據計算出來的偽距離與設定的偽距離閾值Darm進行比較并執行自動避障動作。偽距離閾值的設定影響到避障時臂架與障礙物之間留下的安全裕度空間，初步將偽距離閾值設定為Darm=2 m，最大避障速度vm=5 m/s，閉環反饋參數Ke=diag（10，10，10），仿真時間為20 s。

圖3、圖4所示為未加避障算法時泵車臂架與障礙物之間的最小偽距離和泵車臂架運動姿態軌跡過程。從圖3中可以看出，未加避障算法時，從t=7.21 s開始臂架與障礙物之間的最小偽距離值開始小于0，到t=13.21 s后臂架與障礙物之間的最小偽距離值開始大于0；同時從圖4中可以看到，t∈［7.21，13.21］ s時泵車臂架與障礙物發生碰撞。以上說明未加避障算法時，臂架與障礙物發生碰撞，無法自動躲避障礙物，同時也可說明泵車臂架與障礙物之間的最小偽距離指標能夠反映出泵車臂架與障礙物之間的接近關系。

使用未加關節避障極限方法時，雖然也實現了避障的目標，但是在泵車臂架運動大約10.09 s左右時一臂角度位移超出了其角度位移的最大限定范圍（θ1∈［0，π/2］），無法滿足實際工程條件。而在使用本文避障算法后，如圖6b所示，可以很明顯地看出泵車臂架各臂節轉角很好地限制在限定范圍內。同時可以看到相較未加關節避障極限方法，使用本文避障算法時，泵車臂架一臂轉角變動范圍更小一些，而末節臂轉角變動范圍更大一些，使得一臂運動得更少些，運動更多的是轉動末端幾節臂，這也更加符合實際泵車正常工作時盡量少動一臂的要求，使泵車臂架運動得更加平穩。

由圖5c可知，在使用未加關節避障極限方法時，由于未對泵車臂架關節進行限制，泵車臂架一臂運動范圍較大，一臂關節角速度變化幅值也更大，最大幅值差達到0.06 rad/s，這樣會造成泵車整體臂架運動更加抖動、不平穩。而使用本文避障算法時，如圖6c所示，由于對泵車臂架關節進行了限制，泵車臂架一臂運動范圍更小，一臂關節角加速度變化幅值變小，最大幅值差降為0.02 rad/s。將較大的運動放在末節臂，且由于末節臂相較于其他幾節臂尺寸更小、質量更小、轉動慣量更小，雖然末節臂的關節角速度幅值變大了，但是泵車臂架整體運行得卻更加平穩順滑。

圖6d所示為使用本文避障算法的泵車臂架與障礙物之間的最小偽距離變化曲線。在初始階段，泵車臂架與障礙物之間的最小偽距離值大于設定的偽距離閾值Darm，泵車臂架保持水平運動。當t=5.03 s時泵車臂架與障礙物之間的最小偽距離值開始小于設定的偽距離閾值Darm，此時給泵車臂架添加了一個避障速度，如圖6e所示，泵車臂架運動進入到避障任務階段。由于避障速度的加入，使得t∈［5.03，15.08］ s泵車臂架與障礙物之間的最小偽距離值都保持在偽距離閾值Darm左右并大于零，從而保證泵車臂架一直處在一個安全狀態不與障礙物發生碰撞并留有足夠的安全裕度空間。到t=15.08 s后，泵車臂架與障礙物之間的最小偽距離值開始大于設定的偽距離閾值Darm，避障速度為零，泵車臂架避障階段結束，開始保持原來的水平運動。由圖6f可知，在t∈［0，5.03］ s階段，泵車臂架末端誤差幾乎為零，泵車臂架處于水平運動階段，在t∈［5.03，16.58］ s階段，泵車臂架處于避障階段，為了遠離障礙物從而出現了較大的軌跡誤差，但在t=15.08 s后泵車臂架結束避障運動，由于閉環控制的存在，泵車臂架開始回歸規定的軌跡并在t=16.58 s后回到規定軌跡，泵車臂架末端誤差接近于零，保持了很好的目標軌跡跟隨。

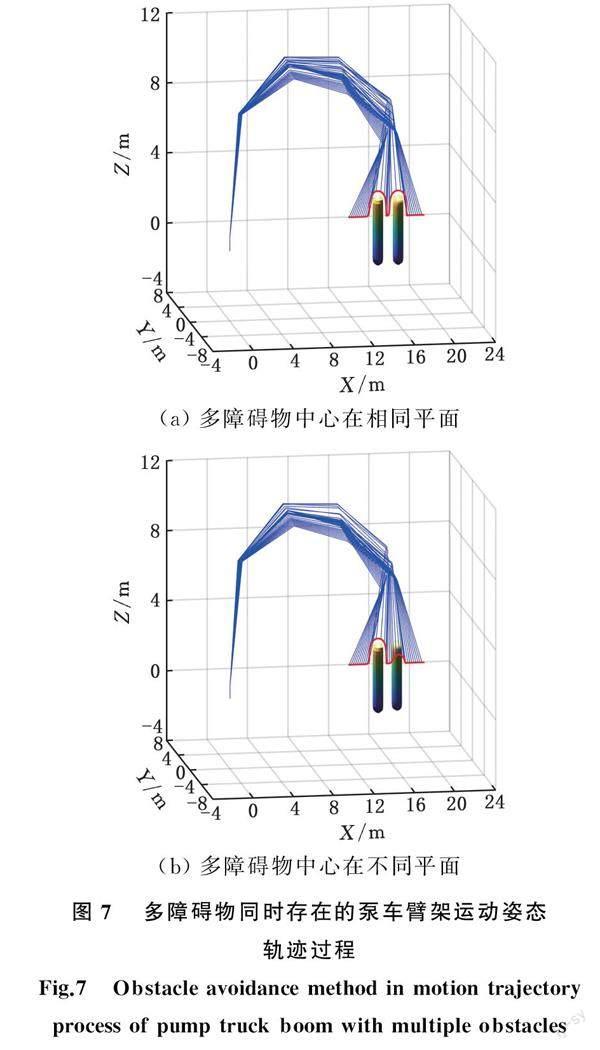
本文算法還可適用于解決多個障礙物同時存在的避障問題，將仿真條件設置為障礙物1和障礙物2大小相同（R=0.25 m， H=2 m），障礙物相同平面分布時障礙物中心坐標分別為（16.5，-0.48，1）m、（14.5，-0.48，1）m，障礙物不同平面分布時障礙物中心坐標分別為（16.5，0，1）m、（14.5，-0.48，1）m，仿真時間設定為30 s，其他仿真條件與之前仿真條件一樣，仿真結果如圖7所示。由仿真結果可以看出本文避障算法能夠實現多障礙物同時存在時的三維避障問題。

3.2 半物理仿真實驗驗證

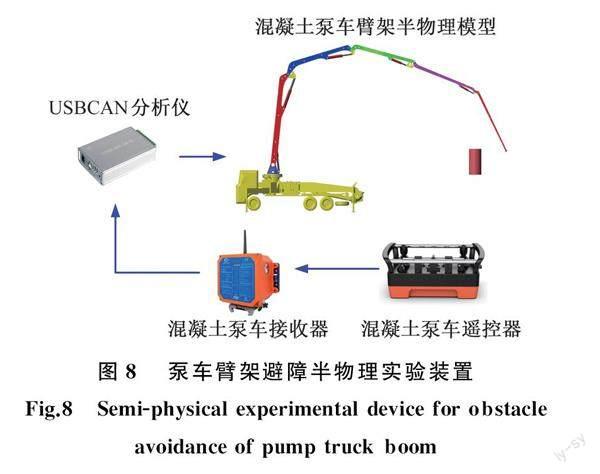
為進一步驗證在考慮混凝土泵車實際物理結構下本文避障算法的有效性，進行半物理仿真實驗。半物理仿真實驗裝置如圖8 所示，物理部分由混凝土泵車臂架遙控器、遙控器信號接收器、USBCAN信號分析儀等組成，虛擬部分是在MATLAB R2021a＼＼Simulink中搭建的混凝土泵車Simulink物理模型。使用實際的混凝土泵車遙控器對泵車臂架末端進行速度和方向控制，觀察記錄泵車臂架運動及避障情況，開展半實物仿真實驗。

混凝土泵車Simulink物理模型中的泵車臂架結構參數、初始臂架位姿角度、初始臂架位置和障礙物位置及大小設置與前文3.1節中相同。偽距離閾值設定為Darm=2 m，最大避障速度vm=5 m/s，閉環反饋參數Ke=diag（10 000，10 000，10 000），采樣頻率為10 Hz，仿真時間為20 s。物理硬件之間通信參數波特率為250 kb/s，臂架末端速度方向和大小由遙控器上萬向比例推桿控制，速度最大值為0.25 m/s。

圖9所示為在Simulink仿真環境中混凝土泵車臂架避障的運動過程，可以看出，在t=12 s左右時，臂架末端跨過障礙物最高點，整個過程臂架末端未與障礙物發生接觸，表明本避障算法能夠有效地實現泵車臂架避障。

圖10所示為泵車臂架半物理仿真實驗結果，可以看出，從t=0.7 s輸入開始，泵車臂架即開始水平運動，到t=2.4 s達到最大速度0.25 m/s，并從t=17.7 s開始減速直到t=19 s時減到零，泵車臂架停止水平運動。由圖10b可以看出，在t∈［6.6，16.8］ s時，臂架末端X方向和Z方向的避障速度不為零，這是因為從t=6.6 s開始泵車臂架與障礙物之間的最小偽距離小于閾值Darm，泵車臂架進入避障運動，到t=16.8 s時最小偽距離開始大于閾值Darm，泵車臂架結束避障運動，如圖10f所示。t∈［6.6，16.8］ s的整個過程中，最小偽距離都大于零，說明泵車臂架不與障礙物發生接觸，有效地實現了安全避障。

同時由圖10b可以看到，在整個避障過程中Z方向的避障速度恒大于零，而在X方向避障速度先大于零后小于零，這是因為在Z方向，臂架需要跨過障礙物，所以Z方向避障速度需要一直大于零。而在X方向臂架末端先是不斷向障礙物靠近，當t=12 s左右時經過障礙物最高點后，臂架末端逐漸遠離障礙物，所以X方向的避障速度先是大于零，阻礙臂架靠近障礙物，然后再小于零，讓臂架更快遠離障礙物，這樣保證在整個避障過程中避障速度總是起到躲避障礙物的作用，從而達到避障的目的。

由圖10c、圖10d 可以看出，在整個實驗過程中，泵車臂架關節角度和角速度變化都保持著連續、平穩，各關節角度都限制在關節極限內，并且第一節臂架的關節角度和關節角速度都變化得很小，這有利于泵車臂架整體的穩定性。在t=6.6 s，由于激活了泵車臂架的避障運動，出現了一個較大的角速度變化，但仍然保持著連續性，并未發生嚴重突變。從圖10e中可以看出，在t=6.6 s之前，臂架末端保持著很高的位置精度，在t=6.6 s后，泵車臂架末端位置誤差開始加大，并且在t=12 s時Z方向上位置誤差達到最大值，這是因為從t=6.6 s開始泵車臂架進行避障，需要犧牲位置精度去進行避障運動，并在t=12 s到達障礙物的最高點處，此時位置誤差達到最大，在t=16.8 s后結束避障運動，泵車臂架執行水平軌跡跟隨運動，臂架各方向位置誤差接近于零，保證了避障結束后能夠保持較高的精度。

綜上可以看出，半物理仿真實驗驗證了本文避障算法能夠有效地實現泵車臂架避障，并且能夠有效地將各關節角度限制在關節極限內，整個避障過程平穩、連續，同時保證了在避障完成后回到原來軌跡上并保持較小的位置誤差。

4 結論

（1）本文提出了一種基于偽距離的混凝土泵車臂架避障方法，采用超二次曲面函數描述空間障礙物，將偽距離作為評價泵車臂架與障礙物接近程度的指標，有效地避免了歐氏距離的復雜運算，提高了計算效率和實時性，成功實現了泵車臂架的避障。

（2）結合工程實際，考慮到混凝土泵車臂架結構的關節限制，在實現泵車臂架避障的同時保證了各臂架關節極限的限制和運動的平穩性。

（3）通過仿真和半物理實驗，驗證了本文提出算法的有效性，同時該算法適用于多空間障礙物避障。

參考文獻：

［1］KRAMER M， ROSMANN C， JOHN F. Time-optimal Unfolding of a Mobile Truck-mounted Concrete Pump under Constraints［J］. Forschung im Ingenieurwesen-Engineering Research， 2018， 82（1）：45-57.

［2］BOTTIN M， ROSATI G. Trajectory Optimization of a Redundant Serial Robot Using Cartesian via Points and Kinematic Decoupling［J］. Robotics， 2019， 8（4）：101.

［3］MENASRI R， NAKI A， DA A B， et al. A Trajectory Planning of Redundant Manipulators Based on Bilevel Optimization［J］. Applied Mathematics & Computation， 2015， 250：934-947.

［4］WOOLFREY J， LU W， LIU D. A Control Method for Joint Torque Minimization of Redundant Manipulators Handling Large External Forces［J］. Journal of Intelligent and Robotic Systems， 2019， 96（1）：3-16.

［5］PATEL R V， SHADPEY F， RANJBARAN F， et al. A Collision Avoidance Scheme for Redundant Manipulators：Theory and Experiments［J］. Journal of Robotic Systems， 2010， 22（12）：737-757.

［6］DAI Y， LEE S G. Formation Control of Mobile Robots with Obstacle Avoidance Based on GOACM Using Onboard Sensors［J］. International Journal of Control Automation & Systems， 2014， 12（5）：1077-1089.

［7］PERDEREAU V， PASSI C， DROUIN M. Real-time Control of Redundant Robotic Manipulators for Mobile Obstacle Avoidance［J］. Robotics & Autonomous Systems， 2002， 41（1）：41-59.

［8］YOSHIDA E， ESTEVES C， BELOUSOV I， et al. Planning 3-D Collision-free Dynamic Robotic Motion through Iterative Reshaping［J］. IEEE Transactions on Robotics， 2008， 24（5）：1186-1198.

［9］BENZAOUI M， CHEKIREB H， TADJINE M. Redundant Robot Manipulator Control with Obstacle Avoidance Using Extended Jacobian Method［C］∥ 18th Mediterranean Conference on Control and Automation.Marrakech：IEEE， 2010：11474038.

［10］GUAN X Q， LIANG G H， NIU K. A Redundant DOFs Manipulator Motion Obstacle Avoidance Algorithm［C］∥International Conference on Automation， Mechanical and Electrical Engineering. Phuket， 2015：242-250.

［11］HU Tianjian， WANG Tianshu， LI Junfeng， et al. Obstacle Avoidance for Redundant Manipulators Utilizing a Backward Quadratic Search Algorithm［J］. International Journal of Advanced Robotic Systems， 2016， 13（119）：353-341.

［12］DE L， AIESSANDRO， KHATIB， et al. A Depth Space Approach for Evaluating Distance to Objects with Application to Human-Robot Collision Avoidance［J］. Journal of Intelligent & Robotic Systems Theory & Application， 2015， 80：7-22.

［13］CHEN Y J， JU M Y， HWANG K S. A Virtual Torque Based Approach to Kinematic Control of Redundant Manipulators［J］. IEEE Transactions on Industrial Electronics， 2016， 64（2）：2334829.

［14］WANG Wenrui， GU Jinlin， ZHU Mingchao. et al. An Obstacle Avoidance Method for Redundant Manipulators Based on Artificial Potential Field［C］∥2018 IEEE International Conference on Mechatronics and Automation（ICMA）. Changchun：IEEE， 2018， 2151-2156.

［15］ZHAO Liangliang， JIANG Zainan， SUN Yongjun， et al. Collision-free Kinematics for Hyper-redundant Manipulators in Dynamic Scenes Using Optimal Velocity Obstacles［J］. International Journal of Advanced Robotic Systems， 2021， 18（1）：185-190.

［16］CHOI S I， KIM B K. Obstacle Avoidance Control for Redundant Manipulators Using Collidability Measure［J］. Robotica， 2000， 18（2）：143-151.

［17］HWANG K S， Ju M Y. 3D Collision-free Motion Based on Collision Index［J］. Journal of Intelligent and Robotic Systems， 2002， 33（1）：45-60.

［18］PATEL R V， SHADPEY F， RANJBARAN F， et al. A Collision-avoidance Scheme for Redundant Manipulators Theory and Experiments［J］. Journal of Robotic Systems， 2005， 22（12）：737-757.

［19］BRICE L B， MAAROUF S， VAHE N. Modeling and Adaptive Control of Redundant Robots［J］. Mathematics and Computers in Simulation， 2006， 71（4/6）：395-403.

［20］MU Zonggao， XU Wenfu， LIANG Bin. Avoidance of Multiple Moving Obstacles during Active Debris Removal Using a Redundant Space Manipulator［J］. International Journal of Control Automation and Systems， 2017， 15（2）：1-12.

［21］牟宗高. 面向狹小空間作業的超冗余機器人軌跡規劃及控制研究［D］. 哈爾濱：哈爾濱工業大學，2017.

MU Zonggao. Research on Trajectory Planning and Control of Hyper-redundant Robots for Confined-space Operation［D］. Harbin：Harbin Institute of Technology， 2017.

（編輯 王艷麗）

作者簡介：

黃 毅，男，1978年生，博士、教授。研究方向為工程機械動力學及控制。 E-mail：tjhuangyi110@163.com。

收稿日期：2022-09-01

基金項目：國家自然科學基金（51875048）