金屬礦山充填開采富水巷道圍巖穩定性控制研究

劉建博，陳昌云

（礦冶科技集團有限公司，北京 100160）

地下巷道處于復雜的地質環境中，巷道穩定性是關乎礦山能否正常生產的重要因素，礦體回采后，會引起圍巖應力的重新分布，可能會導致圍巖發生局部破壞，從而影響巷道的穩定性[1]，準確有效地判斷礦體開挖后是否會造成巷道失穩破壞，是當前采礦工程研究的重點課題之一。國內外專家及學者對巷道的穩定性進行了大量的研究。在理論分析方面，牛少卿等[2]、趙毅鑫等[3]、石永奎等[4]分別基于不同的理論方法，對巷道的支護方式、巷道穩定性影響因素、巷道的穩定性預測等進行了研究。在現場監測方面，聶百勝等[5]、劉強等[6]應用微震監測技術對巷道穩定性及其微震時空能量特性進行了研究；李濤等[7]應用空心包體地應力測量方法對巷道受地應力作用時的破壞規律進行了研究。在數值模擬方面，賈照遠等[8]、夏德威等[9]、楊寧等[10]、張寧等[11]、WU 等[12]借助FLAC3D、ABAQUS、FLAC2D等軟件，針對采動對軟巖巷道、矩形巷道的穩定性進行了模擬研究。

隨著“兩山”理論的提出，充填采礦法以其安全風險低、減少對自然環境的破壞等優勢得到了廣泛應用[13]，大量學者針對充填采礦法進行了研究，其中，趙興東等[14]、曹易恒等[15]、許洪亮等[16]針對充填采礦法的采礦工藝進行了研究；宋宏元等[17]、羅來和等[18]針對充填采礦法采場工藝參數進行了研究；羅方偉等[19]、曾佳龍等[20]、邵明偉等[21]分別針對充填采礦法采場穩定性以及采場地壓管理進行了研究。

前人對巷道穩定性和充填采礦法做了大量研究，但巷道穩定性研究主要針對不存在地下水的情況，現實中，很多礦山都會涉及到地下水的存在；而充填采礦法的研究也多集中在采礦工藝、采場結構參數優化、采場地壓控制等方面，對于充填采礦下巷道穩定性的研究較少。因此，考慮到上述問題，本文基于前人研究成果，考慮地下水存在，采用3Dmine-Rhino-Griddle 軟件進行某礦山礦體與巷道建模，以FLAC3D軟件進行礦體開挖模擬，研究充填開采礦體開挖對巷道穩定性的影響，為礦山穩定性開采提供理論依據。

1 工程地質條件

研究區域內共有分布在6 個礦體群內的39 個礦體：①號礦體群、②號礦體群、③號礦體群、⑤號礦體群、⑦號礦體群、⑧號礦體群。礦體形態簡單，以脈狀產出為主，在研究區域內的主要礦體為①-1 號礦體。①-1 號礦體形態簡單，以大脈狀、大板狀、似層狀為主，局部呈透鏡狀和似層狀，礦體傾向SE，傾角在40°～55°之間，走向14°～24°，產狀穩定，平均厚度30 m，礦體內部基本無脈巖穿插或其他較大構造破壞，構造及脈巖影響程度小，礦體直接上盤為絹英化碎裂巖、絹英巖化花崗質碎裂巖，礦體下盤為黃鐵絹英巖化花崗質碎裂巖或黃鐵絹英巖化碎裂巖，區域內地下水的補給以地表水為主，通過地表裂隙、巖溶裂隙等途經直接補給地下水，巷道圍巖出現滲水現象。

本次開采范圍是采礦范圍內賦存于119 線以東-115～-165 m 間的礦體，考慮地下水的存在，為防止地表出現沉降，確保巷道穩定性，保障礦體回采過程中人員安全，同時最大限度回采礦體，故本次回采應用的采礦方法為高強度的上向進路膠結充填法。采場沿走向布置，長度50 m，采場高度50 m，寬為礦體厚度，留10 m 長礦柱。根據礦體賦存情況，自上而下進行礦體回采，分為3 個步驟，設計首采中段為-115～-131 m，然后逐次開采-131～-147 m 水平、-147～-165 m 水平。分別分析各礦體回采后-105 m 水平巷道和-120 m 水平巷道位移、應力、塑性區的變化情況，同時，借助監測數據對擾動較大區域進行穩定性分析。

2 礦區模型的構建

2.1 模型

利用FLAC3D軟件實現礦體回采模擬，研究滲透壓存在情況下礦體回采對巷道穩定性的影響。基于3Dmine、Rhino-Griddle 軟件，將礦區礦體、巷道、圍巖經過三種軟件的不同功能、不同格式的轉換、網格劃分，最終建成可被FLAC3D軟件識別的模型，通過初始條件以及工況的設定，實現礦體開挖的模擬，模型構建流程如圖1 所示，模型效果如圖2所示，監測點布置如圖3 所示。

圖1 數值模型構建流程圖Fig.1 Flow chart of numerical model construction

圖2 數值模型Fig.2 Numerical model

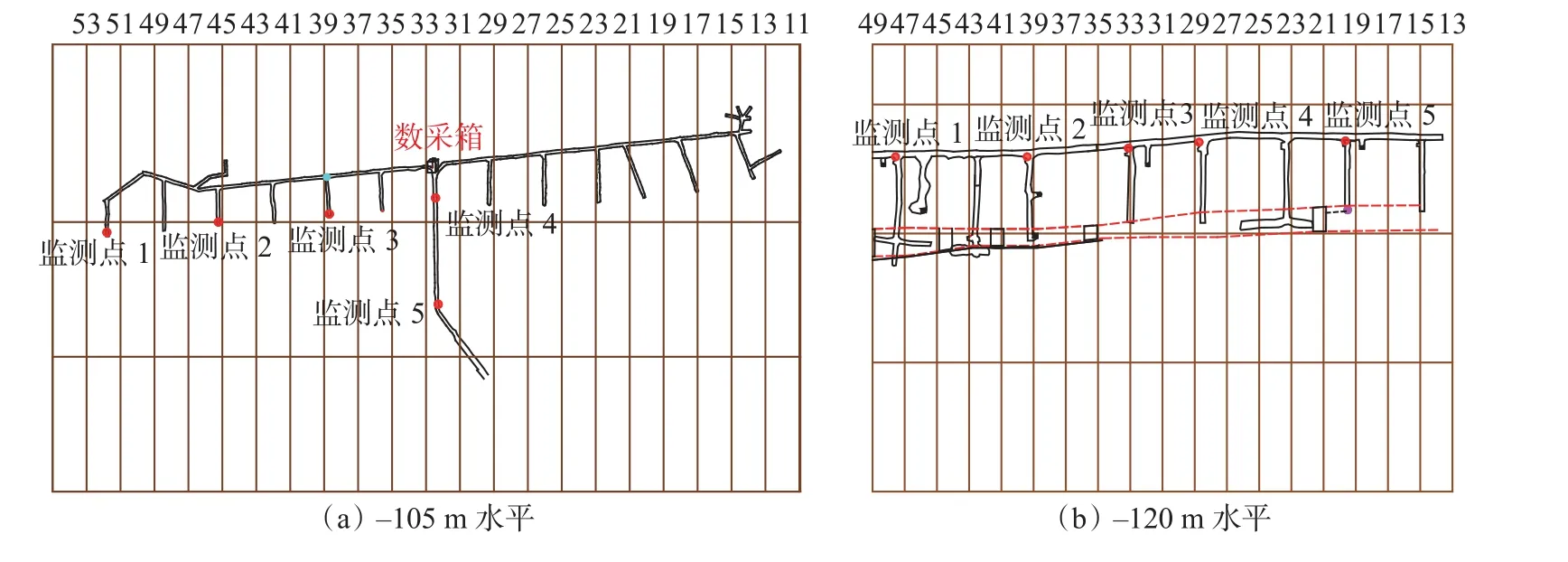
圖3 不同水平分段巷道監測點布置圖Fig.3 Layout of monitoring points in different horizontal segmented roadways

2.2 基本力學參數

在實際礦山中，由于巖石與巖體尺寸存在差異，同時礦體和圍巖的賦存環境有可能存在對其具有腐蝕作用的化學物質以及會受到頻繁采動的影響和開挖過程中巖體會受到風化作用等，本文應用Hoek-Brown 強度準則進行巖石力學參數折減，得到最終符合實際礦山的巖石力學參數，見表1。通過查閱礦區資料，得到充填體力學參數，見表2。

表1 巖體基本力學參數Table 1 Basic mechanical parameters of rock mass

表2 充填體力學參數Table 2 Parameters of filling mechanics

2.3 初始地應力的生成

基于前人對礦區地應力的調查，地應力變化均呈線性增長趨勢（圖4），且具有最大主應力>垂直應力>最小主應力的特點；此外，考慮礦區內賦存大量地下水，故進行滲透壓生成。本次模型最深處深度為-240 m，按圖4 所示公式進行初始地應力計算，最大主應力為13.046 MPa，最小主應力為4.474 MPa，垂直主應力為7.640 MPa，滲透壓力為2.350 MPa。

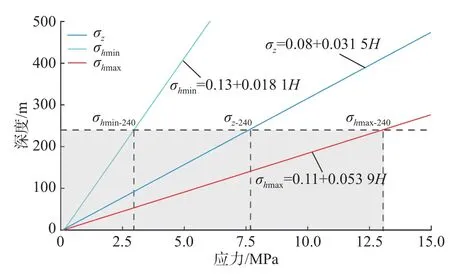
圖4 初始地應力Fig.4 Initial ground stress

3 數值模擬結果分析

3.1 位移分析

結合模擬結果，分別對兩水平巷道各步驟回采后的頂板及邊幫沉降變形情況進行統計分析，結果如圖5 和圖6 所示，規定整體變形量大于10 mm 區域為回采過程擾動較大的區域，整體變形量小于10 mm區域為回采過程中擾動較小區域。

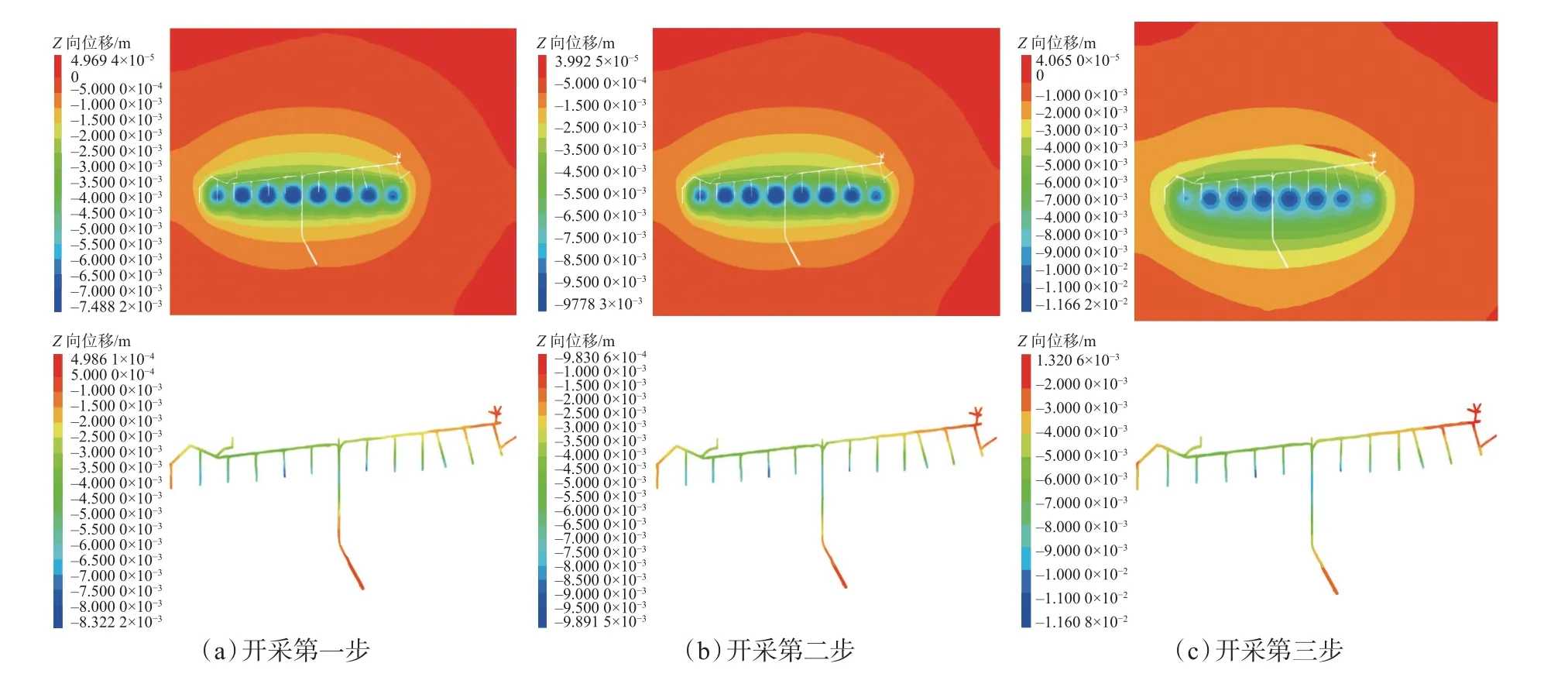
圖5 -105 m 水平巷道各步驟位移變化規律Fig.5 Displacement change laws of each step in -105 m horizontal roadway

圖6 -120 m 水平巷道各步驟位移變化規律Fig.6 Displacement change laws of each step in -120 m horizontal roadway

第一步回采結束后，兩水平巷道頂板及邊幫均產生了較大位移，-105 m 水平巷道邊幫最大沉降變形量為7.49 mm，位于各采場正上方或靠近采場采聯位置處，頂板最大沉降變形量為8.32 mm，位于39 線采聯端部，原因在于其處于采場正上方中心位置，因此受礦體回采擾動影響最大，而位于礦柱上方的采聯或距離礦柱較近的采聯，其頂板、邊幫沉降變形量均較小，-105 m 水平巷道主巷道由于距離采場較遠，其變形量較小，在4 mm 左右；-120 m 水平巷道變化相對-105 m 水平巷道則較小，主巷道由于距離采場較遠，其頂板、邊幫沉降變形量均較小，在2～3 mm之間，由于在礦體回采完畢后，對與采場連接的采聯部分進行了及時的充填，因此控制住了采聯沉降變形量進一步擴大，頂板、邊幫最大變形量在3 mm 左右。第二步回采結束后，兩水平巷道沉降變形量均較第一步回采結束后大幅度降低，-105 m 水平巷道最大沉降變形量增加2.29 mm，-105 m 水平主巷道沉降變形量基本未增大，39 線采聯端部沉降變形量最大，邊幫沉降變形量為9.78 mm，頂板沉降變形量為9.89 mm，其余各條采聯相較第一步回采后基本未產生較大變形；-120 m 水平巷道由于礦體回采結束后及時對空區進行充填以及其距離采場較遠，因此未產生較大變形，主巷道頂板及邊幫最大沉降變形量仍保持在2～3 mm，各條采聯頂板最大沉降變形量在3 mm 左右，分別是位于29 線與37 線之間的采聯，其原因在于相較于其他采聯，這幾條采聯距離采場較近，因此所受擾動也較大。第三步回采結束后，兩水平巷道的沉降變形量進一步增大，-105 m 水平巷道最大變形量達到11.66 mm，頂板最大沉降位移達到11.6 mm，位于39 線采聯端部位置，其余位置變形量增量較小，頂板及邊幫變形均小于10 mm；-120 m水平巷道受擾動影響相對較小，其邊幫最大沉降位移為3 mm，與第二步回采完畢后相同，而頂板沉降位移有所增加，最大值達到3.48 mm，位于39 線、33 線、29 線采聯端部位置。

整體上，隨著回采步驟的增加，兩水平巷道的沉降變形量均呈逐漸增大趨勢，而增加量則呈逐漸減小趨勢，由于-105 m 水平巷道39 線采聯位于采場正上方，因此其受擾動影響最大，超過了10 mm，在回采過程中應著重關注此處位置，及時采取相應措施控制其變形量的進一步擴大，同時，由于及時對采場進行了充填，避免了兩水平巷道變形量的進一步擴大。

匯總各監測點下沉數據可知各監測點沉降變形隨回采步驟進行呈現增大趨勢，且同步增大（圖7）。

圖7 位移監測數據Fig.7 Monitoring data of displacement

1）-105 m 水平巷道：監測點1 監測51 線至53 線之間采聯端部頂板沉降，第一步回采引起頂板產生較大沉降變形，變形量為1.05 mm，后續回采其變形量呈線性增長，最終穩定在3.48 mm；監測點2 監測45 線采聯端部頂板沉降，由于其位于采場正上方的邊緣，第一步回采引起其產生急劇下沉，下沉量達5.8 mm，由于采用充填法回采，避免了第一步回采產生更大的沉降變形，第二步回采、第三步回采對其影響較小，但沉降變形量仍持續增加，最終穩定在8.61 mm；監測點3 監測39 線采聯端部頂板沉降，由于其位于采場的正上方，其受采動影響最大，第一步回采結束后，其沉降變形量達到7.2 mm，第二步回采、第三步回采對其產生的影響相對第一步回采較小，回采結束后，其變形量達到10.39 mm；監測點4 監測33 線采聯中間位置頂板沉降，由于其位于采場正上方的邊緣位置，其沉降變形量較監測點3 小，第一步回采結束后，其變形量達到5.8 mm，第二步回采、第三步回采結束后，其變形量最終穩定在8.89 mm；監測點5 監測33 線采場上盤采聯頂板沉降，由于其距離采場較遠，故礦體回采對其產生的影響相對較小，第一步回采結束后，其變形量為1 mm，回采結束后，其變形量穩定在3.6 mm。

2）-120 m 水平巷道：監測點1 監測47 線采聯與主巷道交叉口頂板沉降，由于其距礦房中心位置較遠，回采初期，頂板受短暫時間的拉應力影響，出現些許向上的變形，但隨著回采的進行，拉應力轉化為壓應力，頂板由向上的變形轉變為沉降變形，最終沉降變形量在第三步回采結束后穩定在2.18 mm；監測點2 監測39 線采聯與主巷道交叉口頂板沉降，其變形規律與監測點1 相同，均先產生向上變形，后轉變為沉降變形，但由于其距礦房中心位置較近，回采結束后，沉降變形量穩定在2.99 mm；監測點3 監測33線采聯與主巷道交叉頂板沉降，隨著回采的進行，其最終沉降變形量穩定在2.67 mm；監測點4 監測29 線采聯與主巷道交叉口頂板沉降，回采對其產生的影響相對較小，回采完畢后，其最終沉降變形量穩定在1.14 mm；監測點5 監測19 線采聯與主巷道交叉口頂板沉降，其變形規律與監測點4 相同，回采結束后，其最終沉降變形量穩定在2.12 mm。

3.2 應力分析

圖8 為-105 m 水平巷道、-120 m 水平巷道所受最大壓應力與最大拉應力隨著回采步驟進行的變化規律。由圖8 可知，隨著礦體的回采充填，兩水平巷道的最大壓應力（-105 m 水平巷道：R2=0.998 9；-120 m水平巷道：R2=0.997 71）和最大拉應力（-105 m 水平巷道：R2=0.995 8；-120 m 水平巷道：R2=0.941 06）均呈指數形式增長，其增長速率呈現先增大后減小趨勢，但-105 m 水平巷道所受最大壓應力和最大拉應力增長速率均大于-120 m 水平巷道，隨著礦體回采步驟的進行，對巷道所受最大壓應力影響較大，當礦體回采完畢后，兩水平巷道所受最大壓應力和最大拉應力均達到峰值，其中，-105 m 水平巷道所受最大壓應力值為17.8 MPa，最大拉應力值為1.8 MPa，-120 m 水平巷道所受最大壓應力值為11.5 MPa，最大拉應力值為0.37 MPa。基于受力可知，-105 m 水平所受最大壓應力和最大拉應力已接近巷道圍巖的抗壓、抗拉強度，壓應力、拉應力最大區域位于39 線采聯端部位置，其沉降變形也較大，一旦超過抗壓強度，必然會導致該位置產生破壞，-120 m 水平巷道所受壓應力、拉應力值均較小，且均未超過巖體強度，因此，從受力來看，-120 m 水平巷道保持在穩定狀態，綜上所述，說明采用充填法進行礦體的開采，可以有效維持圍巖的穩定性，避免兩水平巷道受到破壞。

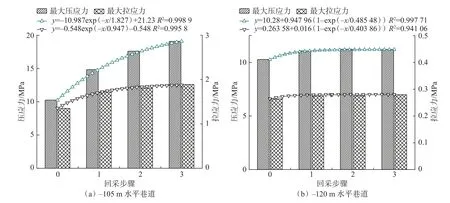
圖8 各步驟應力變化Fig.8 Stress variation at each step

進一步分析各開采步驟下滲透壓的變化規律，選取兩水平巷道在各步驟礦體回采結束后所受滲透壓最大值進行統計分析，結果如圖9 所示。由圖9 可知，隨著回采步驟的進行，兩水平巷道滲透壓呈指數增長規律（-105 m 水平巷道：R2=0.999 8；-120 m 水平巷道：R2=0.999 93），滲透壓總體呈增大趨勢，在第一步礦體回采完畢后，滲透壓增大速率較快，且-105 m水平巷道增大速率與增大值均大于-120 m 水平巷道，在后續回采步驟中，兩水平巷道滲透壓增加速率逐漸減小，在礦體全部回采完畢后，-105 m 水平巷道滲透壓為1.72 MPa，較未回采之前，滲透壓增加0.82 MPa，-120 m 水平巷道滲透壓為1.82 MPa，較未回采之前滲透壓增加0.17 MPa。由于礦巖受到回采擾動，導致巖體的孔隙水壓力產生應力集中現象，會對巷道穩定性產生嚴重影響，從而加劇巷道發生失穩的可能性，因此，針對巷道受力及變形較大位置（-105 m 水平巷道29 線、35 線、39 線采聯，-120 m水平巷道29 線、33 線、39 線采聯），應采取必要加固手段保證其穩定性，避免造成人員和財產的損失。

圖9 各步驟滲透壓變化Fig.9 Osmotic pressure changes at each step

3.3 塑性區分析

圖10 為塑性區隨回采變化規律圖，在回采過程中以拉伸破壞為主，剪切破壞次之，其中拉伸破壞主要出現在采場上、下盤圍巖中，剪切破壞出現在上盤圍巖中，兩水平巷道附近發生的塑性破壞極少，且主要為拉伸破壞，考慮由于滲透壓的影響導致巖體強度降低，部分巖體出現破壞，但破壞范圍較小，巷道整體保持穩定狀態。拉伸破壞在第一步回采、第二步回采過程中增長較快，在第三步回采過程中增長態勢變緩，基本與第二步回采后所產生的塑性區體積相同，剪切破壞在第一步回采、第二步回采過程中增長緩慢，在第三步回采過程中急劇增長。回采結束后應及時對采空區進行充填，避免塑性破壞區域延伸到兩水平巷道周圍。

圖10 塑性區變化規律Fig.10 Change law of plastic zone

3.4 現場位移監測對比

本次監測點布置與-105 m 水平巷道、-120 m 水平巷道數值模擬過程中監測點布置一致，分別監測各步驟礦體回采后相應位置變形情況，監測設備選用單點位移計（圖11）。

圖11 單點位移計布設Fig.11 Layout of single point displacement meter

在各步驟礦體回采完畢后，提取監測數據，并對數據進行整理，獲取穩定后數據，分別得到-105 m 水平巷道、-120 m 水平巷道位移變化規律圖（圖12）。由圖12 可知，隨著回采的進行，兩水平巷道各監測點位移變化規律均呈現逐漸增大趨勢，-105 m 水平巷道變形最大位置出現在監測點3 位置處（39 線采聯端部），實際監測沉降變形量為10.5 mm，與模擬數據10.39 mm 相差1%左右，其余監測點變形量與模擬數據相比變化范圍均在1%左右；-120 m 水平巷道其最大沉降變形位置出現在監測點2 位置處（39 線采聯與主巷道交叉口處），實際監測變形量為2.8 mm，與模擬數據2.99 mm 相比變化6%左右，其余監測點與模擬數據相比變化范圍也均在6%左右，由于-120 m 水平巷道整體位移較小，因此，模擬結果與實際變形量相差較小，通過對比模擬數據與實際位移變形監測數據可知，模擬結果監測點沉降變形發展規律及變形量與實際監測數據發展規律及變形量基本吻合，表明通過數值模擬預測的兩水平巷道變形量較為合理，因此，在后續回采過程中可在此基礎上進行下一步模擬，確保礦體回采過程中兩水平巷道處于穩定狀態。

圖12 位移變形規律Fig.12 Deformation law of displacement

4 結論

1）基于3Dmine-Rhino-Griddle-FLAC3D分析方法，可以對含水礦山礦體回采過程中巷道穩定性進行有效分析，從而為含水礦山礦體回采過程中確保巷道穩定性提供理論依據。

2）分別進行三步驟礦體回采模擬。礦體的回采引起兩水平巷道產生沉降變形，隨著回采的進行，兩水平巷道沉降變形均逐漸增大，每步回采引起的沉降變形量則逐漸減小，礦體回采完畢后，-105 m 水平巷道39 線采聯端部沉降變形量最大，為11.66 mm，其余部位沉降變形量小于10 mm；-120 m 水平巷道受擾動相對較小，其最大沉降變形量在3 mm 左右，采空區的及時充填有效地阻止了變形量的進一步擴大。

3）兩水平巷道所受最大壓應力、最大拉應力隨著回采步驟的增加呈指數增長規律，礦體回采完畢后，-105 m 水平巷道所受最大壓應力值為17.8 MPa，最大拉應力值為1.8 MPa，-120 m 水平巷道所受最大壓應力值為11.5 MPa，最大拉應力值為0.37 MPa，與位移變形位置相對應，兩水平巷道所受最大壓應力和最大拉應力基本處于穩定狀態。隨著回采的進行，兩水平巷道滲透壓均呈現指數增長狀態，回采過程中，滲透壓較大區域均出現在各個采聯兩幫位置處，距離采場位置較遠的主巷道處，滲透壓基本保持初始滲透壓狀態。

4）結合應力和塑性區分布可知，雖然巷道圍巖所受應力并未超過巖石強度，但由于存在滲透壓，兩水平巷道在拐角位置及部分采聯端部位置出現塑性破壞，但塑性區范圍較小，表明滲透壓對巖石強度存在弱化作用，因此，在-105 m 水平巷道及-120 m 水平巷道變形、受力較大位置應及時采取相應措施，避免在礦體回采過程中造成更大的破壞。

5）通過模擬與實際監測數據對比可知，數值模擬可準確模擬礦體回采過程中兩水平巷道穩定狀態，數值模擬結果可為含水礦山穩定性開采提供理論依據。