基于數據映射優化的航空機匣變形測量偏差比對

劉 輝， 梁 晉， 葉美圖， 郭建英， 李磊剛

（1. 西安交通大學 機械工程學院 機械制造系統工程國家重點實驗室，陜西 西安 710049；2. 新拓三維技術（深圳）有限公司 創新實驗室，廣東 深圳 518060；3. 中國航發四川燃氣渦輪研究院 強度傳動試驗研究室，四川 綿陽 621000）

1 引言

中介機匣是航空發動機上的重要承力結構［1］，其承載眾多，結構復雜，所處位置特殊。因此，對機匣的安全性能的試驗及評估已成為航空發動機結構設計和優化中不可或缺的一環。在過去的幾十年里，有限元仿真為中介機匣的靜力變形分析提供了極大幫助，得到了廣泛應用。同時，除傳統的千分表、應變片等手段外，光學非接觸測量方法的數字圖像相關（Digital Image Correlation， DIC）技術也能夠獲得機匣試驗過程中的實時變形信息［2-3］。然而，在DIC 測量中，受諸如非均勻環境光、被測物自振等隨機因素干擾，實測結果往往難以與仿真保持一致。因此，研究一種DIC測量變形與有限元模擬變形相互比對、相互驗證的系統性方法，對于中介機匣的可靠性評估和結構優化設計具有十分重要的意義［4］。

目前，已有大量學者使用數字圖像相關法實現有限元仿真模型的建立和比對驗證。Gardner［5］等人為驗證NASA 建立的火箭殼體屈曲設計因子和高保真度模擬方案的正確性，使用數字圖像相關法獲取大型金屬復合材料圓柱殼體的強度測試數據，以驗證仿真模型的正確性。加州大學Mohammad［6］等人為構建肺部的生物力學數值模型，使用DIC 系統測量豬肺穩定膨脹周期的表面變形數據，從而校準有限元模型的仿真參數。美國陸軍航空與導彈中心的Owens［7］等人為了提取一種橡膠增韌環氧基膠材料混合斷裂模型的J 積分和應力強度因子，將DIC 測得的位移數據映射到有限元模型中，以測得更加可靠的裂紋參數。阿爾伯塔大學Li［8］等人為建立能夠指導雙金屬晶格結構設計的有限元模型，使用DIC 方法對316L 不銹鋼雙金屬復合材料的拉伸和壓縮變形進行測量，從而驗證了數值模型的正確性。然而，模擬數據和DIC 數據之間存在著一些固有差異，在進行有意義的定量比對之前，必須校正這些數據差異，例如數據坐標系，網格類型和節點位置，測量的空間分辨率、數據濾波方法和應變計算類型等，而上述的所有研究中均未系統地給出有效的數據處理方法。從數據結構的角度來看，對于有限元數據和DIC 數據之間的對比驗證，一種方法是使用一組基函數分解有限元數據和實驗數據，對比分解基函數序列的振幅［9-12］，其優點是對比計算的數據量小，缺點是難以保證所分解的基函數能夠完全代表實驗或仿真數據。MatchID NV 公司的Pascal［13］等人提出一種借助有限元仿真數據生成試件表面的虛擬變形散斑圖像進行數據對比的方法，雖然該方法能夠自然地消除DIC 網格和有限元網格在應力計算、空間分辨率和濾波效果等方面的不一致，但通過貼圖的方式生成虛擬圖像不僅會消耗大量的計算資源，而且貼圖本身存在著難以完全和DIC 網格對齊的缺陷，使得偏差比對結果的可靠性降低。因此，目前還需進一步研究更加魯棒且操作簡便的用于有限元驗證的數據處理方法。

本文為了精確量化航空發動機機匣剛度試驗中利用雙目DIC 測量全場變形的整體偏差，提出了一種系統、全面的DIC 測量數據與有限元（Finite Element Method， FEM）仿真數據之間的映射方法。以有限元仿真結果為準，并以機匣肋板處的變形為例，首先使用FPFH 特征和迭代最近點法（Iterative Closets Points， ICP）解算出兩類點云數據之間的相對位姿，進而完成數據的坐標對齊；然后使用遺傳算法優化神經網絡，完成了仿真網格數據向DIC 網格數據的高精度映射，從而消除了網格空隙帶來的比對誤差；最后，使用逐點最小二乘應變估計算法統一了有限元模擬和DIC 測量的應變計算模式，得到與DIC 屬性一致的有限元比對數據，最終實現肋板處全場變形的測量偏差比對。

2 機匣變形測量偏差比對原理

本文所提出的偏差比對原理的目標是消除有限元（FEM）仿真數據和DIC 測量數據之間的固有不一致，如二者在世界坐標系位置，網格類型和節點位置，測量的空間分辨率、數據濾波方法和應變計算類型上的差異，從而利用有限元仿真數據和真實測量數據完成有意義的偏差對比驗證，實現有限元仿真與DIC 測量結果的相互印證與閉環分析。

2.1 數據映射優化

為了消除有限元仿真數據和測量數據之間的不一致問題，首先要完成兩組數據的映射優化，實現有限元數據向DIC 測量數據的映射。使用FPFH 特征和ICP 算法進行FEM 點云和DIC點云的位姿解算，從而實現兩類數據的坐標統一，然后使用遺傳算法優化的擬合神經網絡，完成FEM 網格數據向DIC 網格數據的映射，具體流程如圖1 所示。

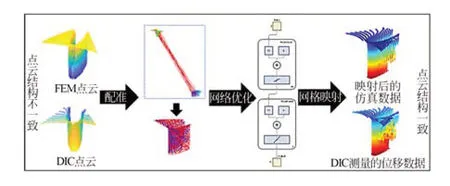
圖1 數據映射優化原理Fig. 1 Principles of data mapping optimization

2.1.1 基于點云配準的全局坐標統一

在進行坐標統一的過程中，全站儀、激光跟蹤儀等傳統測量設備難以滿足機匣變形的測量要求。首先，測量對象在加載過程中會產生形變，其形狀并不固定，難以在被測物上布置跟隨機匣變形的標記，也難以在有限元模型上找到其精確的對應點。其次，全站儀、激光跟蹤儀等很難在現場進行在線校正，且由于不能進行離線計算，其單次測量時間受激光三角測距的計算時間影響，遠遠高于攝影測量所需時間，往往難以滿足機匣動態剛度測試所要求的時間分辨率限制。此外，通過這種方式測量出的位置數據難以和DIC 測頭的測量數據保持同步，造成對齊精度不可控，誤差來源不可溯等問題。而采用點云配準的方式進行坐標對齊，不僅不用額外架設其他測量設備，避免了復雜的現場布置和設備校正等操作，同時，點云配準數據和變形數據是天然對應的，誤差大小和來源是可溯源的。綜合上述原因，本文采用點云配準方法進行數據坐標的全局統一，算法步驟如下：

（1）基于FPFH 特征粗配準。

FPFH 算子具有高效穩定的特征表達性能，在具有顯著姿態差異的配準任務中具有較強的優勢。根據FPFH 特征查找到的特征點可用于FEM 點云和DIC 點云相對位姿初值的計算，計算公式如式（1）所示：

其中：XFEM是FEM 點云上的特征點，XDIC是DIC點云上對應于FEM 點云的特征點，T1是從DIC點云變換到FEM 點云的剛性變換初值，實現點云粗配準。

（2）基于ICP 算法的精配準。

為保證兩組點云相對位姿的求解精度，還需使用ICP 算法對初始變換后的兩組點云進行迭代優化［14-15］，本文采用迭代最近點法（Iterative Closets Points，ICP）令待配準的DIC 點云為集合P={pi}，i=1，2，3，…，n，基準FEM 點云集合為X={xi}，i=1，2，3，…，m。為了確立兩個點云之間的對應點，構建點云KD 樹查找所有空間最近點，以此計算點集P到點集X之間的位姿變換關系，迭代的優化方程如式（2）所示：

其中：ni是xi點所在局部平面的法向量，R為點集P到X之間的旋轉矩陣，T為點集P到點集X的平移向量。

2.1.2 FEM 與DIC 的網格映射原理

一般情況下，待比對的FEM 網格和DIC 網格類型和節點位置都不相同，為了完成偏差比對必須首先完成網格映射。DIC 數據節點的三維坐標是通過雙目測頭重建的機匣肋板表面點云，其數據類型是一個曲面，而有限元仿真的模型點云是一個三維實體，其中不僅包含表面位移數據，同時也包含體內位移數據。在實際轉換的過程中，FEM 空間點云中的表面點云和內部點云難以區分，若采用直接插值的方法，FEM 表面節點將會受到內部節點位移量的影響，從而與DIC算法模型特征產生新的不一致，在比對的過程中引入額外偏差。此外，不同的插值類型對不同表面形狀的插值結果差異較大，難以找到針對所有表面形狀的最佳插值方法。而BP 神經網絡通過機器學習的方式進行空間位移場的擬合，可以根據訓練集數據調整出最佳的模型參數。因此，在這種情況下，相比于插值方法，使用神經網絡對有限元仿真模型（理論真值）的空間位移場進行擬合是一種更加通用、方便的數據映射策略。

綜上所述，為避免引入額外偏差，本文采用遺傳算法優化神經網絡［16-18］擬合FEM 的空間位移場，根據配準后的DIC 節點坐標，將有限元網格映射至DIC 網格上。算法的具體流程如圖2 所示。用于FEM 向DIC 的數據映射優化建模步驟如下：

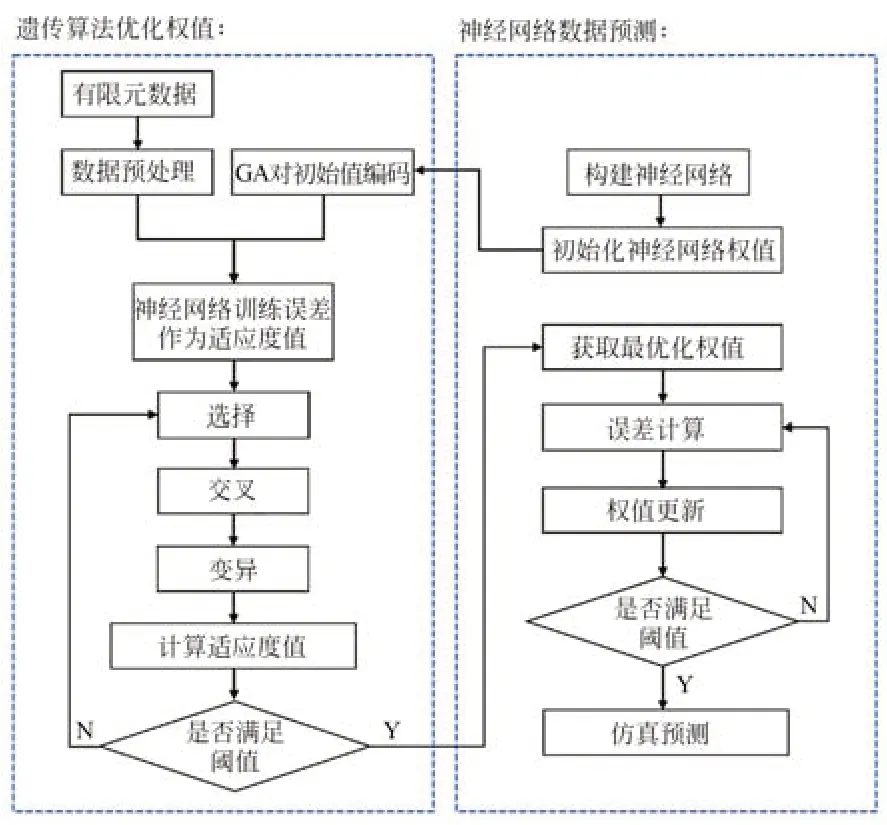
圖2 遺傳算法優化神經網絡Fig.2 Neural network optimized by genetic algorithm

（1）構建BP 神經網絡參數。

出于對計算效率的考慮，本文采用結構為3-25-3 的神經網絡進行擬合，即輸入層有3 個節點，隱藏層由25 個節點組成，輸出層有3 個節點。激活函數使用Sigmoid 激活函數。神經網絡結構如圖3 所示。

（2）遺傳算法優化神經網絡權值和閾值。

通過對神經網絡中的所有權值進行編碼，獲得單個權值序列［s1，s2，s3，…，sL］和閾值序列［γ1，γ2，γ3，…，γL］。將所有閾值和權重按順序拼接形成一個染色體。染色體的長度計算公式如式（3）所示：

其中：ni為輸入層節點數，n為隱藏層節點數，n0為輸出層節點數。在本文中，輸入層有3 個節點，隱藏層有25 個節點，輸出層有3 個節點，因此每條染色體的長度為3×25+25+25×3+3=178。

遺傳方法包括選擇、交叉和變異。選擇操作一般使用輪盤賭等方法產生新種群。交叉操作產生最佳性狀的重要手段，如果令兩條染色體XiA和XiB相互交叉，那么新個體如式（4）所示：

其中：α＜Pc且0 ＜α＜1，Pc為父母染色體發生交叉的概率。

此外，本文使用均勻突變操作，將突變概率設置為Pm，設置突變點xk的范圍為［Ukmin，Ukmax］，突變點的新遺傳值如式（5）所示。

其中，r是［0，1］范圍內的隨機數。

（3）訓練BP 神經網絡。

通過將網絡權值和閾值導入遺傳算法中進行優化，得到新的權值和參數，將其分配給BP 神經網絡。然后根據BP 算法，輸入訓練集進行學習和訓練，直到預測誤差滿足期望值。

有限元數據作為一種數值模型，其數據相對與DIC 數據具有以下兩點優勢：①數據分辨率：有限元仿真是一個理論模型，其計算的分辨率原則上可以取到無窮小，而立體DIC 的測量數據分辨率受到鏡頭分辨率，像元尺寸，測量幅面大小等因素的制約，存在一個最小極限。根據精度比對的慣例做法，一般傾向于將分辨率（精度位數）更高的數據作為基準。②環境噪聲：有限元模型是理論模型，其計算數據不包含噪聲，以此擬合出的空間位移場能夠完全對應于原始數據，將其作為比對基準是可靠的。而DIC 測量數據包含了環境噪聲，如果用DIC 數據作為訓練集擬合其空間位移場，噪聲部分會對擬合結果造成較大影響，以此作為比對基準是不可靠的。此外，DIC數據作為待驗證數據，理應維持其原始測量值，得到更直觀的偏差計算結果。

由于以上原因，本文將有限元節點坐標及其對應的位移值作為訓練集，擬合得到空間內與FEM 數據關聯的連續位移場，然后將DIC 節點坐標作為輸入進行預測，輸出節點位移量，從而完成從有限元網格向DIC 網格的映射。

2.2 空間變形計算原理

數字圖像相關法（DIC）直接測量得到的位移數據往往含有一定噪聲，而由FEM 得到的數據不包含噪聲，這導致了二者在應變計算方法上的差異，為了消除這種差異，本文統一對兩組位移數據使用空間逐點最小二乘應變估計算法［19］，計算Green-Lagrange 應變張量，以此保證偏差比對的同一性和有效性，Green-Lagrange 應變張量計算公式如式（6）所示：

其中：(u，v，w)為當前點的位移，(X，Y，Z)為當前點的三維坐標，εxx，εyy，εzz，γxy，γxz，γyz為當前點在空間內的格林應變張量。

式（6）中的位移梯度對噪聲敏感，為了消除噪聲，本文擴展了Pan［19］等人提出的應變窗思想，將三維位移數據進行平面投影濾波，即使用位移數據(u，v，w)組成的最小二乘擬合的超平面參數求解位移梯度數據，超平面方程如式（7）所示：

其中：(x0，y0，z0) 是當前應變窗的中心點，(x，y，z)為當前點的空間坐標，(up，vp，wp)為當前點的空間位移。

本文在目標點云區域劃分空間球體區域作為計算應變的應變窗，將點云數據帶入式（7），即可求解出該應變窗在空間內3 個方向上位移擬合超平面，通過超平面參數確定濾波后的位移梯度，用于式（6）中的格林應變張量的計算。根據計算出的Green-Lagrange 應變張量，進而計算出當前空間點的3 個主應變。當前空間點的主應變ε1，ε2，ε3即為方程（8）的解：

其中，J1，J2，J3為應變張量不變量，計算公式如式（9）所示：

3 測量試驗與結果

中介機匣結構特殊，內外環呈規則圓形，環壁厚低于0.5 cm，且二者之間由數個周向均布的對稱弧形肋板連接。肋板本體在機匣內外壁的連接處截面和厚度均最小，因此在機匣性能試驗中，匣體的整個肋板及與內外壁的連接部位屬于最薄弱處，極易引起應力集中，是試驗任務的主要關注點。精確量化其承載后的變形信息對結構安全性能評估和優化設計具有重要意義。因此，本文以頂部肋板處的DIC 和FEM 數據進行驗證和分析。

3.1 視覺變形測量及有限元仿真

3.1.1 試驗系統搭建

本文使用新拓三維（XTOP）的立體DIC 系統（XTDIC?）測量航空發動機機匣頂部肋板的全場變形。測量系統由兩套雙目視覺測量單元組成，相機分辨率為2 448×2 048 pixel，像元尺寸為3.45 μm/pixel，配備鏡頭型號為RICOH，焦距為25.0 mm，相機之間的立體角為25.5°。兩套雙目DIC 設備分別拍攝肋板的左右兩面，使用馬克筆在待測的頂部肋板上點涂用于匹配的散斑特征，重建出的肋板點云拼接通過兩套雙目相機的全局統一標定實現，具體的實驗場景及制作的散斑特征如圖4 所示。

圖4 機匣實驗場景Fig.4 Testing site of casing

機匣的主要的承載部位是呈180°分布的兩個肋板。肋板本體呈對稱圓弧形，在內外壁的連接處截面最小、壁最薄，中間部位截面和壁厚略微增大，是本次試驗任務的關注重點。本文使用結構靜力與疲勞試驗器對機匣進行加載，加載裝置和加載方式如圖5 所示，最大加載載荷為-40 kN，加載過程如圖6 所示。

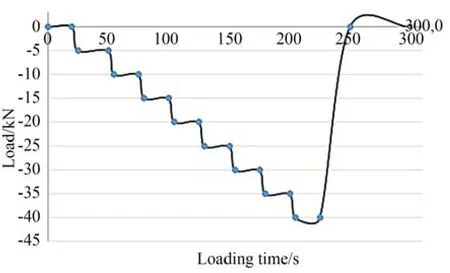
圖6 加載曲線Fig.6 Loading curve

3.1.2 視覺測量結果及有限元仿真結果

兩套DIC 設備測量的頂部肋板位移場和應變場如圖7 所示。從圖中可以看出，雖然兩側位移場分布基本一致，但肋板右側位移數據分布不均勻，存在一定的測量偏差。

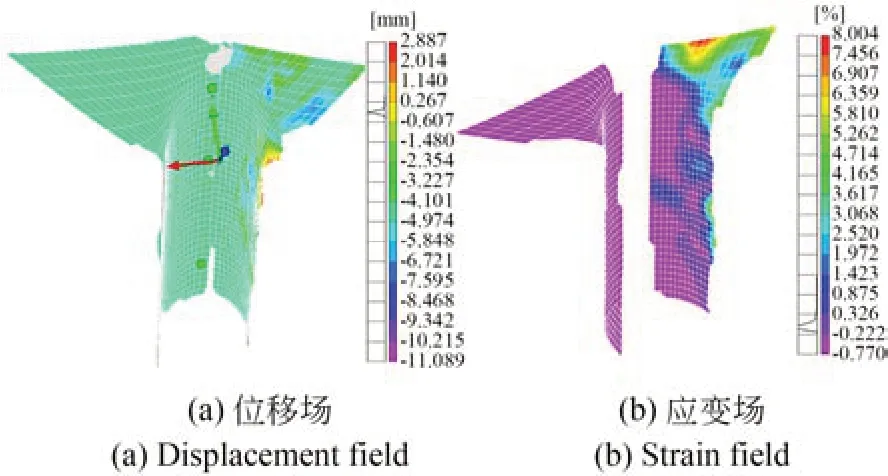
圖7 DIC 測量結果Fig.7 DIC measurement results

使用有限元方法，在相同的邊界條件下對機匣模型進行靜力學仿真分析。模型材料選擇鈦合金，材料密度為4 620 kg/m3，楊氏模量為9.6×1010Pa。使用四面體網格劃分CAD 模型，如圖8（a）所示。對機匣外圈整體施加支撐約束。載荷以線積分的形式施加在機匣內圈的下半圈，如圖8（b）所示，載荷大小隨θ按照余弦變化，載荷施加條件滿足式（10）的約束。

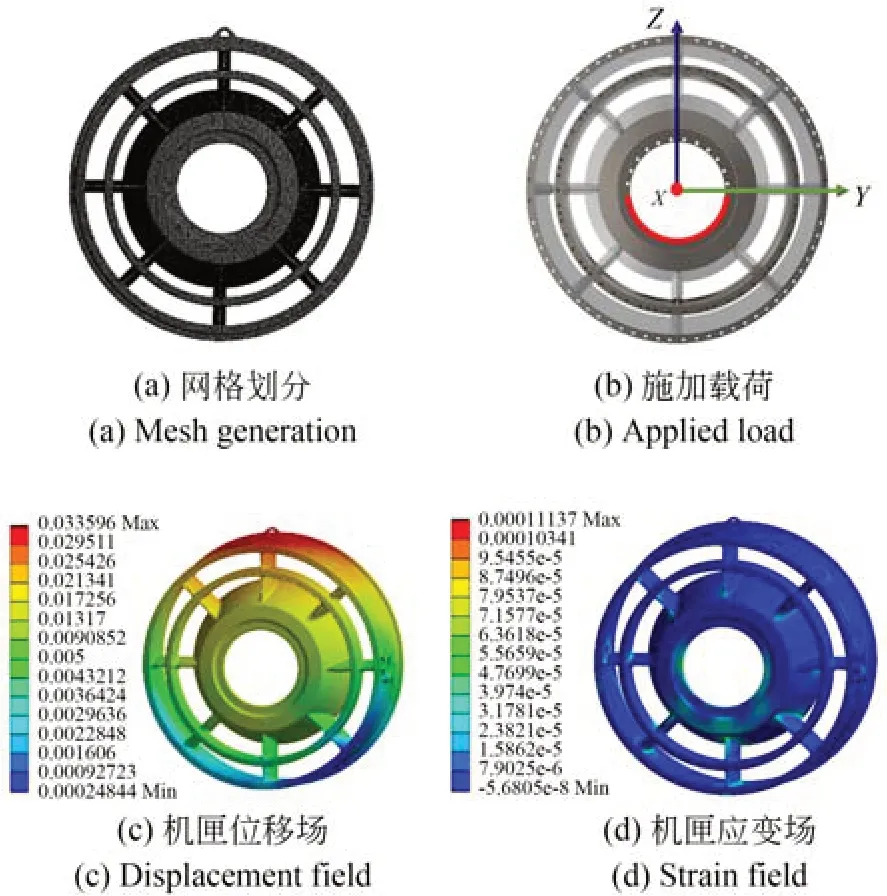
圖8 有限元仿真結果Fig.8 FEM simulation results

其中：fz(θ)為豎直方向的分力，F為當前時刻加載裝置施加的壓力，a為余弦分力的幅值，可根據約束條件求出。

最終得到如圖8（b）和圖8（c）所示的仿真結果。從圖中可以看出，仿真得到的最大位移量為0.033 596 mm，最大主應變為111.37με。

3.2 機匣測量偏差比對

3.2.1 數據坐標統一與映射優化

由于DIC 重建出的肋板數據和FEM 仿真得到的肋板數據是在不同坐標系下描述的，直接對比各自x，y，z三個方向的變形分量沒有意義，因此需要將DIC 數據和FEM 數據統一到一個全局坐標系中描述。采用2.1 節中所述的方法完成兩組點云的坐標統一。

分別計算空間中兩幅點云的FPFH 特征，搜索得到兩組點云對應的特征點，從而進行點云相對位姿初值的計算，如圖9 所示，然后使用ICP 算法進一步對位姿初值進行迭代優化。

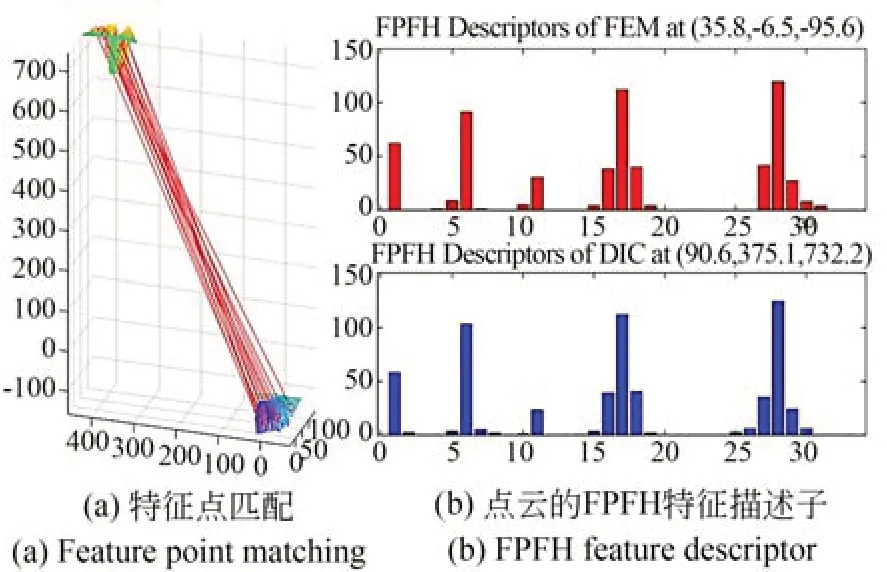
圖9 FPFH 特征匹配Fig.9 FPFH feature matching

由特征點計算出粗配準變換矩陣，粗配準后使用ICP 算法對配準位姿進行迭代優化，精配準后兩組點云之間點距的均方誤差為0.101 5 mm，配準效果良好。粗配準和精配準的效果如圖10所示。

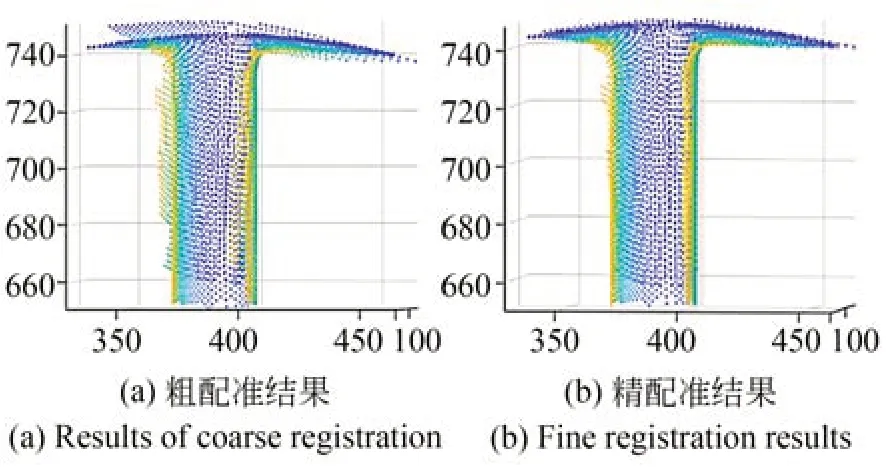
圖10 點云配準效果Fig.10 Point cloud registration results

3.2.2 數據映射及精度驗證

由于DIC 網格和有限元網格在劃分時即存在固有不一致，因此在比對前還需進行DIC 網格和FEM 網格的映射和轉換。

本文使用遺傳算法優化神經網絡實現不同網格之間的轉化。將有限元模型的仿真數據作為訓練集，輸入網絡進行訓練后，再將DIC 網格節點輸入網絡，得到FEM 在DIC 節點處對應的仿真數據，從而預測FEM 網格向DIC 網格的轉換。驗證集的預測效果如圖11 所示。從圖12 中可以看出，擬合神經網絡的預測效果良好，在驗證集上的輸出的誤差小于1×10-6mm。

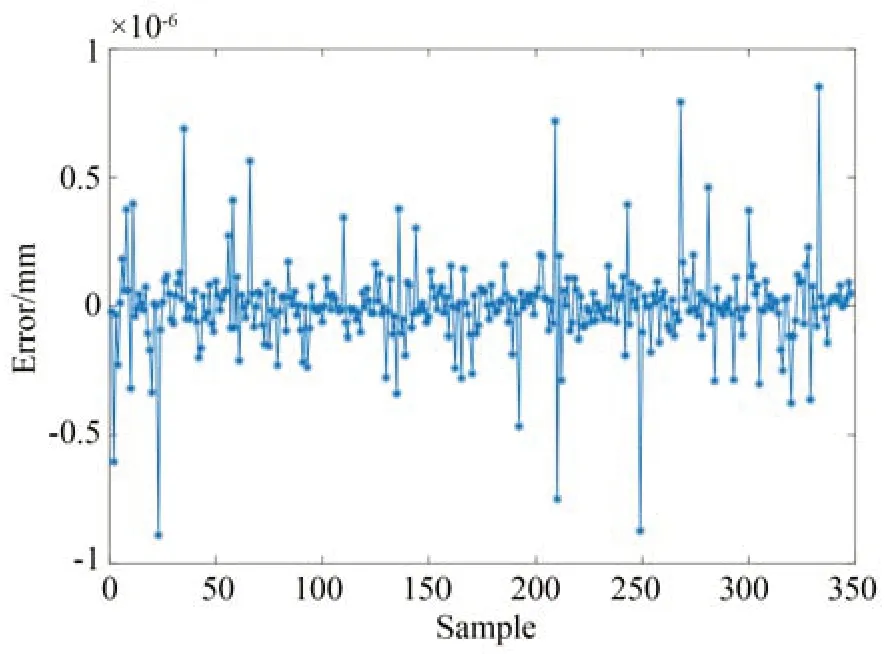
圖12 神經網絡的預測誤差Fig.12 Prediction error of neural network

此外，同時使用自然鄰域插值方法、最近鄰插值和線性插值方法［20］進行網格映射，以對比本方法的映射精度和映射效率。有限元網格為空間四面體網格，DIC 網格為平面四邊形網格，如圖13 所示。每一個DIC 網格節點位移的理論真值通過其所在四面體網格節點插值得到。

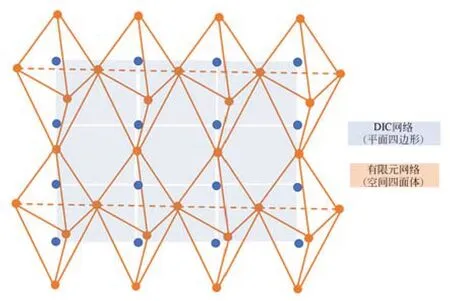
圖13 DIC 網格和有限元網格示意圖Fig.13 Schematic diagram of DIC grid and finite element grid

在FEM 點云中隨機選取12 組點云作為驗證集，同時驗證神經網絡預測結果和插值結果的計算精度，表1 列出了12 組驗證集上不同方法的效果。從表1 中可以看出BP 神經網絡的數據映射誤差最小，自然鄰域插值方法的誤差小于其他插值方法。從標準差上來看，BP 神經網絡數據略小于自然鄰域插值。

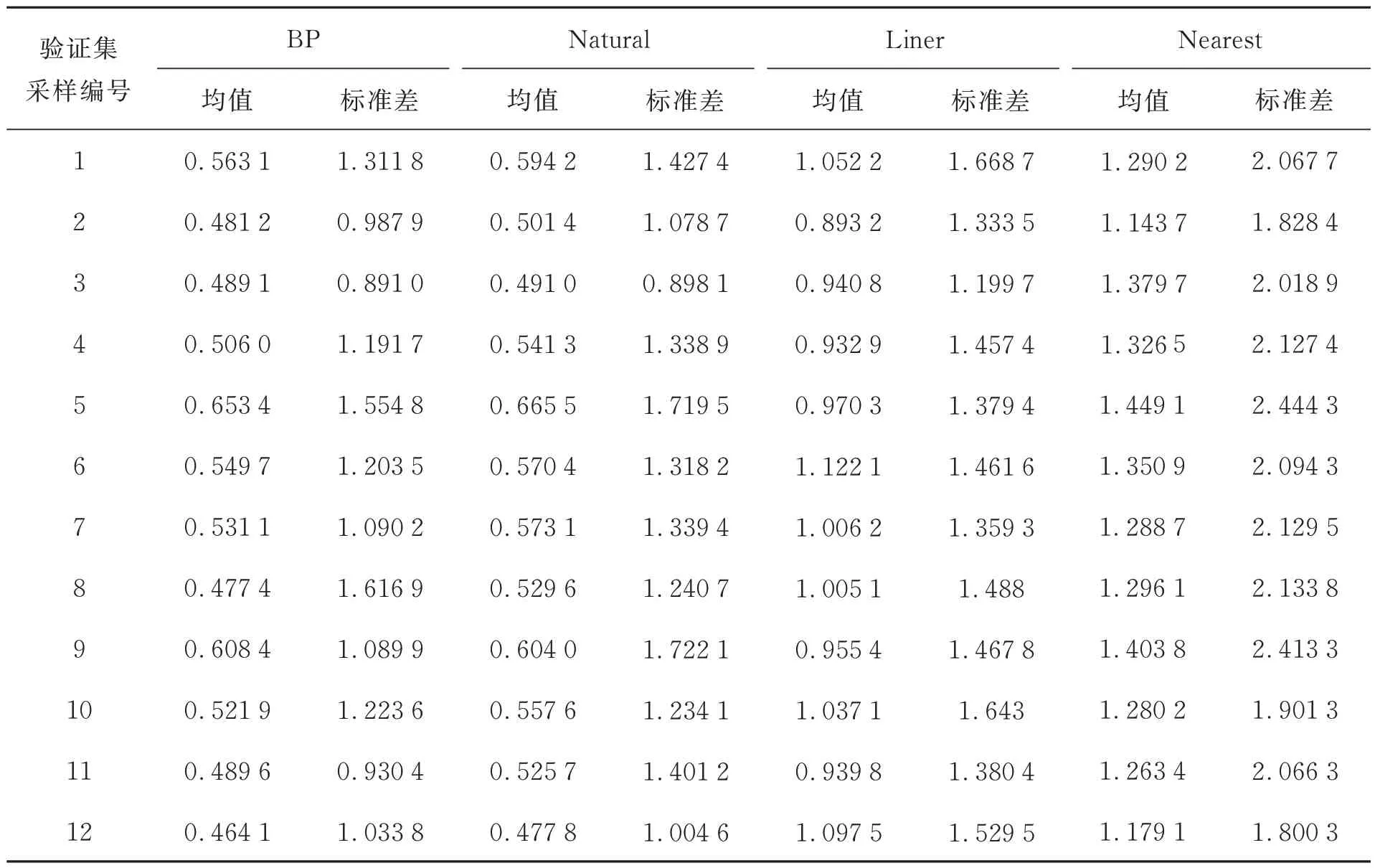
表1 不同方法的數據映射誤差Tab.1 Data mapping error for different methods（10-6 mm）

圖14 顯示了本文方法和自然鄰域插值方法在驗證集上的百分比誤差，從圖中可以看出，本文方法誤差不超過2%，而表現最優的插值方法的誤差最大超過了3%，證明了本文方法在精度上優于其他插值方法。

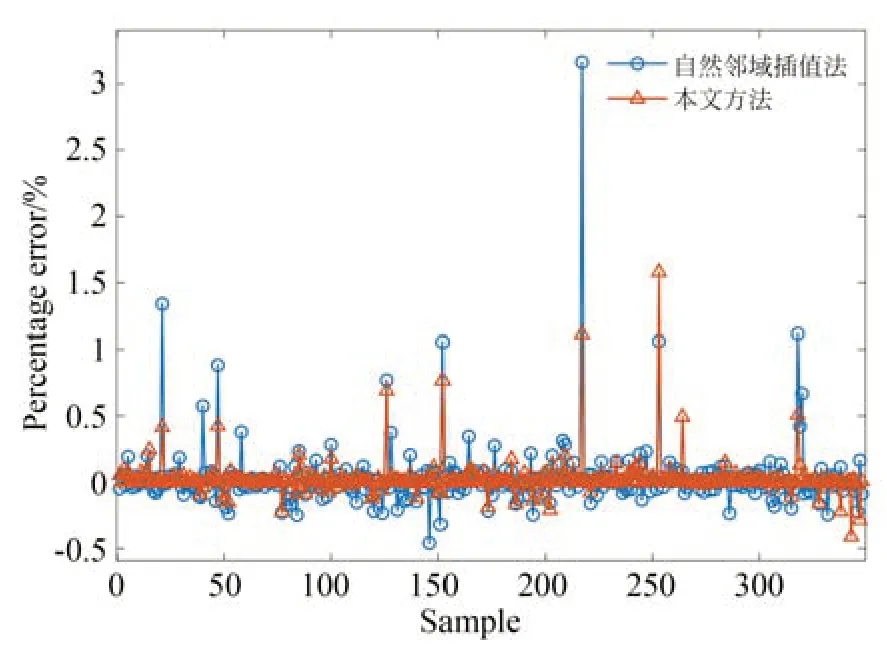
圖14 網格映射的百分比誤差Fig.14 Percentage error in grid mapping

在時間效率上，分別對本文方法、自然鄰域插值法、最近鄰插值法和三線性插值進行分析，在驗證集上（350 個點）程序運算時間統計如表2所示。從表2 中可以看出，本文方法的計算時間遠遠少于其他插值方法，計算效率較高，更加適用于對大型數據進行處理。

表2 計算時間效率分析Tab.2 Computational time efficiency analysis （s）

映射前后的有限元位移場如圖15 所示。映射后的FEM 數據與DIC 數據在空間坐標位置完全對應，有效消除了FEM 和DIC 數據之間的世界坐標系位置，網格類型和節點位置和測量的空間分辨率的不一致。

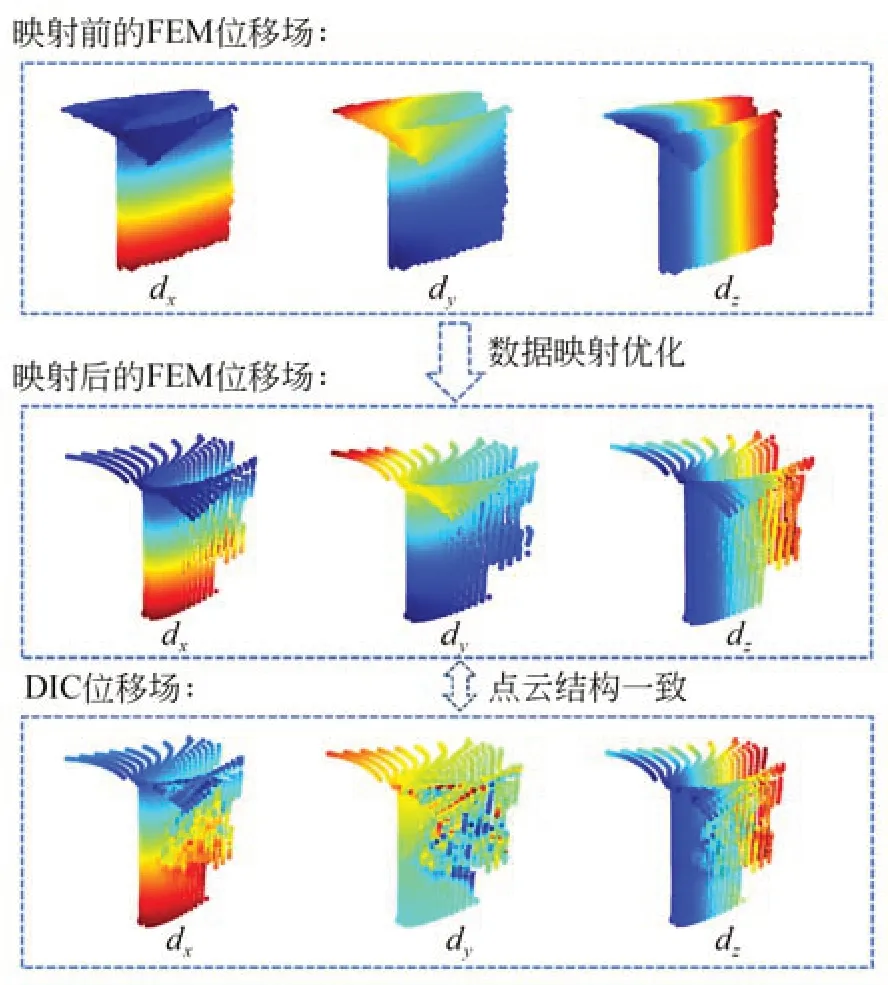
圖15 數據映射優化結果Fig.15 Data mapping optimization results

3.2.3 空間變形計算與偏差對比

本文使用空間包圍球作為點云數據的應變窗，使用逐點最小二乘應變估計算法計算DIC 位移數據的應變量。同時，為保證數據的統一性，對FEM 位移數據進行同步處理，最后實現有限元仿真數據和DIC 測量數據的閉環分析和相互印證。

本文對比FEM 和DIC 數據的3 個主應變ε1，ε2，ε3，變形偏差場的比對結果如表3 所示。使用DIC 測量的應變數據在肋板右側面和右上方存在較大的偏差，說明了在視覺測量過程中，測量肋板右側面的雙目立體DIC 設備存在較大的環境噪聲干擾。經過對實驗現場環境分析，得出噪聲來源如下：①實驗所使用的雙目DIC 設備采用工業灰度相機，對藍光更為敏感，所以每臺DIC 都配備了藍光光源照射被測表面，而肋板右側面正對窗戶，相對于左側受到了更大程度的環境光干擾，因此偏差較大。②機匣加載方式為階梯式加載，在每次啟動加載和保持載荷的瞬間存在一定震蕩，引入了一定的測量誤差。

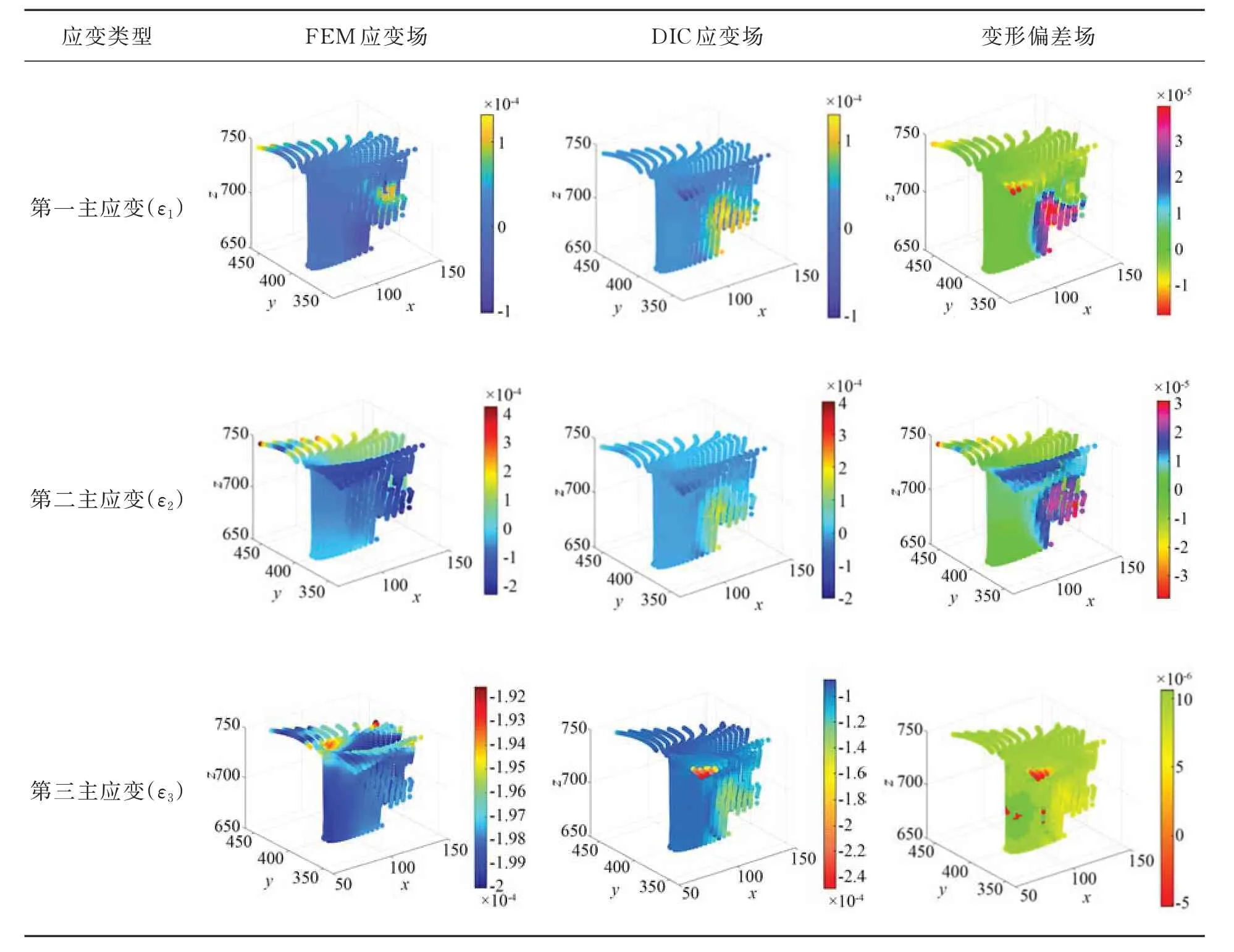
表3 全場變形偏差比對結果Tab.3 Full-field deformation deviation comparison

將DIC 測量的第一主應變和FEM 仿真的第一主應變進行定量的偏差比對結果如圖16 和圖17 所示。從圖16 中可以看出，本次機匣變形的視覺測量結果和有限元仿真表現出較強的一致性，證明了有限元模型的正確性，同時也證明了該實驗中DIC 方法測量的機匣變形數據的準確性。從圖17 中可以看出，以有限元仿真結果為基準，在本次實驗中，DIC 應變測量系統的測量偏差小于50 με。

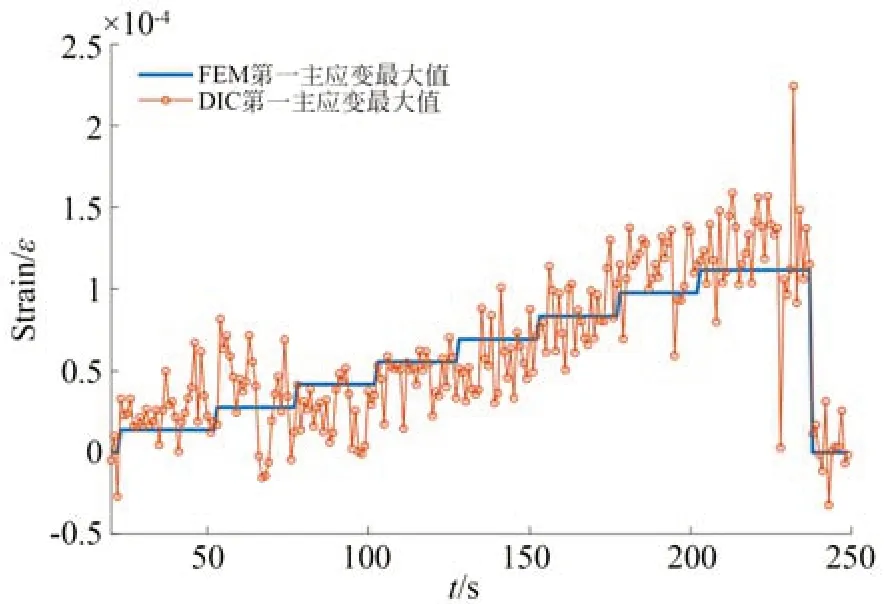
圖16 FEM 和DIC 的第一主應變最大值Fig.16 maximum principal strain of FEM and DIC

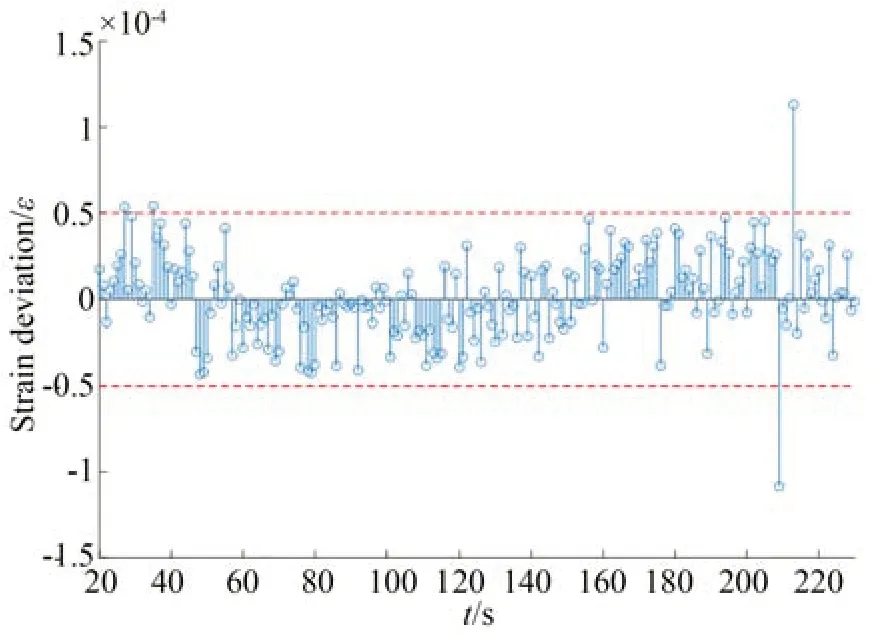
圖17 應變比對偏差Fig.17 Deviation of strain comparison

此外，從整體算法流程和數據結果上看，本文提出的方法相對于其他方法，諸如基函數分解方法和散斑貼圖方法具有其特有的優勢。基函數分解方法是指使用一組基函數分解有限元數據和實驗數據，對比分解基函數序列的振幅，其優點是對比計算量小，但計算結果無法反映偏差的具體位置，而本文方法可以直觀地顯示DIC 測量偏差存在的具體位置。相比于散斑貼圖的方法，本文方法操作簡單。散斑貼圖是人為主觀對齊DIC 計算的感興趣區域，難以保證和度量對齊精度，而本文采用ICP 算法進行對齊，誤差來源可溯可控，節點映射精度更高。

4 結 論

本文提出了一種系統、全面的DIC 測量數據與有限元仿真數據之間的映射方法。可有效的消除DIC 數據和有限元數據在世界坐標系位置，網格類型和節點位置，測量的空間分辨率、數據濾波方法和應變計算類型上的固有差異，實現了有限元仿真和DIC 全場測量的偏差比對。采用“虛實結合”的方式，構建了有限元仿真和DIC 光學測量的閉環分析方法，使二者之間能夠相互印證。

從航空機匣肋板測量偏差比對試驗中可以看出，本文所提方法的網格節點的映射精度優于1×10-6mm，映射百分比誤差小于2%，優于其他各類插值方法。此外，本文算法的數據映射速度較快，在進行數據量較大的比對任務時具有一定的時間效率優勢。仿真變形和DIC 變形的偏差云圖與偏差曲線具有良好的一致性，且能夠顯示DIC 測量偏差存在的具體位置。此外，本文所提方法具有較強的通用性，可以用于但不僅限于機匣肋板的偏差比對，在未來航空發動機機匣及類匣體的研制和測試領域中具有良好的應用前景。