具有輸出約束的多機(jī)械臂系統(tǒng)模糊控制器設(shè)計(jì)
范永青,張占磊
(西安郵電大學(xué) 自動(dòng)化學(xué)院,陜西 西安 710121)
機(jī)械臂是一種通過程序移動(dòng)并操控機(jī)械手進(jìn)行抓/放操作的裝置。隨著計(jì)算機(jī)的發(fā)展,機(jī)械臂被應(yīng)用在生態(tài)系統(tǒng)監(jiān)測[1]、航空航天[2]和醫(yī)學(xué)工程[3]等工程領(lǐng)域。機(jī)械臂作為機(jī)器人系統(tǒng)中的重要組成部分,可以執(zhí)行工業(yè)裝配、安全防爆和醫(yī)療協(xié)助等工作。目前,對機(jī)械臂的研究主要集中在作用任務(wù)物體時(shí)實(shí)現(xiàn)精準(zhǔn)的控制。文獻(xiàn)[4]通過采用人機(jī)接口,提出了一種精確搬運(yùn)物體的控制方法。文獻(xiàn)[5-6]指出在不受外界因素影響的條件下,雖然精確校準(zhǔn)過的機(jī)械臂也能夠確保控制過程中系統(tǒng)的穩(wěn)定性,但當(dāng)外部環(huán)境和設(shè)備磨損、電流波動(dòng)及信號延遲等內(nèi)部參數(shù)變化時(shí),系統(tǒng)的控制性能通常是不穩(wěn)定的,這使得校準(zhǔn)過的系統(tǒng)運(yùn)動(dòng)適應(yīng)性較差。同時(shí),機(jī)械臂系統(tǒng)的工作場景往往是高度非線性的,如在工程應(yīng)用中,當(dāng)機(jī)械臂抓取多個(gè)不同尺寸的物體時(shí),機(jī)械臂的動(dòng)力學(xué)參數(shù)會(huì)發(fā)生較大的變化,因此這類系統(tǒng)被稱為動(dòng)力學(xué)方程未知的機(jī)械臂系統(tǒng)。為了使機(jī)械臂廣泛應(yīng)用于非線性的工作場景,研究動(dòng)力學(xué)方程未知的機(jī)械臂系統(tǒng)成為實(shí)現(xiàn)精準(zhǔn)控制的一個(gè)重要內(nèi)容。
在動(dòng)力學(xué)方程未知的機(jī)械臂系統(tǒng)中,為解決非線性問題,常用的方法有模糊邏輯系統(tǒng)(Fuzzy Logic System,FLS)和徑向基函數(shù),其中FLS中的推理機(jī)制能夠?qū)⒛承┲R轉(zhuǎn)化成人類能力,如學(xué)習(xí)、適應(yīng)、容錯(cuò)和并行[7-8]。根據(jù)這一特性促使許多研究者提出了用于處理不確定性的有效自適應(yīng)控制器[9-10]。但是,FLS的萬能逼近原理[11]只適用于一些特定的域內(nèi),如果系統(tǒng)狀態(tài)超出該域,自適應(yīng)控制的能力將會(huì)減弱,只能保證系統(tǒng)狀態(tài)半全局一致最終有界(Semi-Globally Uniformly Ultimately Bounded,SGUUB)。對于局限于特定域內(nèi)的機(jī)械臂而言,設(shè)計(jì)不受定義域所約束的通用控制器更能符合實(shí)際工業(yè)中的需要。例如,當(dāng)未知函數(shù)的狀態(tài)擴(kuò)展到FLS域外時(shí), Hwang[12]設(shè)計(jì)了一種模糊自適應(yīng)方法實(shí)現(xiàn)全局漸近跟蹤穩(wěn)定,但該方法通過FLS逼近未知非線性項(xiàng)時(shí)需要大量的模糊規(guī)則。為了減少模糊規(guī)則產(chǎn)生龐大的在線計(jì)算量,文獻(xiàn)[13]提出了一種具有少量規(guī)則的全局自適應(yīng)模糊一致性控制器,這種控制方法能保證系統(tǒng)中的所有信號一致最終有界(Uniformly Ultimately Bounded,UUB),并可以減輕具有不確定性的一階和二階多智能體系統(tǒng)的計(jì)算負(fù)擔(dān)。在文獻(xiàn)[12-14]中,指出全局自適應(yīng)控制方法通常適用于某些類型的結(jié)構(gòu)系統(tǒng),如移動(dòng)機(jī)械臂和單輸入單輸出非線性系統(tǒng),在針對較復(fù)雜的被控系統(tǒng)時(shí),設(shè)計(jì)一種不僅具有少量模糊規(guī)則,還能有較高逼近精度的全局模糊自適應(yīng)控制器更具廣泛性。
機(jī)械臂的研究可分為關(guān)于單機(jī)械臂與多機(jī)械臂的研究,在處理分揀、搬運(yùn)小型物體等過程中,單機(jī)械臂的系統(tǒng)就能夠?qū)崿F(xiàn),還可以降低硬件成本。但是,在處理需要協(xié)調(diào)操作及搬運(yùn)大型物體的任務(wù)時(shí),達(dá)不到多機(jī)械臂系統(tǒng)的控制效果,因此多機(jī)械臂的協(xié)調(diào)控制研究受到廣泛關(guān)注[15-16]。文獻(xiàn)[17]提出了一種半分散模糊自適應(yīng)控制方法,用于多機(jī)械臂在運(yùn)動(dòng)和內(nèi)力跟蹤下的協(xié)作問題。Yang等[18]使用近似雅可比矩陣估計(jì)雙臂機(jī)器人的模糊控制,其中一些模糊邏輯系統(tǒng)補(bǔ)償了非線性項(xiàng)的不確定性。對于多機(jī)械臂抓取一個(gè)共同物體的跟蹤問題,設(shè)計(jì)了一種基于阻抗法的新型分散自適應(yīng)模糊控制系統(tǒng)[19]。Li等[20]對于多機(jī)械臂協(xié)作搬運(yùn)具有阻抗作用的物體時(shí),提出了一種基于合并干擾觀測器的分散自適應(yīng)模糊控制。近年來,對多機(jī)械臂攜帶物體運(yùn)動(dòng)問題的研究發(fā)現(xiàn),物體的位置往往會(huì)受到空間因素的約束,超出這些約束會(huì)導(dǎo)致系統(tǒng)的性能下降,甚至可能導(dǎo)致系統(tǒng)損壞。考慮到被控對象的安全性能,需要對系統(tǒng)的輸出進(jìn)行約束,選擇合適的積分障礙李雅普諾夫函數(shù)(Integral Barrier Lyapunov Function,IBLF)既能避免違反輸出限制,又能使系統(tǒng)不遭到破壞。文獻(xiàn)[21]提出了一種具有約束的多機(jī)械臂基于模糊神經(jīng)網(wǎng)絡(luò)的控制方法,通過 IBLF的穩(wěn)定條件設(shè)計(jì)相應(yīng)的自適應(yīng)律,保證了系統(tǒng)跟蹤誤差一致最終有界。在文獻(xiàn)[22]中,針對具有輸出約束的多機(jī)械臂系統(tǒng),提出了一種自適應(yīng)神經(jīng)網(wǎng)絡(luò)的方法,通過IBLF解決環(huán)境限制所產(chǎn)生的約束。因此,在設(shè)計(jì)具有輸出約束的機(jī)械臂控制方法時(shí),采用IBLF的穩(wěn)定性條件能夠很好地改善約束問題。但是,這些研究所設(shè)計(jì)的自適應(yīng)律數(shù)量多,為了減少自適應(yīng)律的數(shù)量,則需要考慮在多機(jī)械臂系統(tǒng)研究中加入一個(gè)非零時(shí)變參數(shù)。
針對具有輸出約束的多機(jī)械臂協(xié)調(diào)搬運(yùn)同一物體時(shí)軌跡跟蹤問題,擬設(shè)計(jì)一種基于IBLF的模糊自適應(yīng)控制器。該控制器采用具有非零參數(shù)的FLS萬能逼近原理估計(jì)系統(tǒng)中的非線性項(xiàng),并通過IBLF的穩(wěn)定性條件構(gòu)造能夠在線更新的自適應(yīng)律。當(dāng)系統(tǒng)狀態(tài)超出FLS逼近域時(shí),利用滑模控制將域外的狀態(tài)量拉回到域內(nèi),保證閉環(huán)系統(tǒng)中的所有信號一致最終有界。為了驗(yàn)證模糊自適應(yīng)控制器的有效性,在常數(shù)約束條件下,將其與自適應(yīng)控制器和模糊比例微分(Proportional Derivative,PD)控制器進(jìn)行位置跟蹤軌跡對比。
1 系統(tǒng)描述
1.1 機(jī)械臂介紹
系統(tǒng)動(dòng)力學(xué)方程需要聯(lián)立機(jī)械臂動(dòng)力學(xué)方程與物體動(dòng)力學(xué)方程,其中第i個(gè)n自由度機(jī)械臂的動(dòng)力學(xué)方程[23]為

(1)
式中:ri=[ri1,ri2,…,rin]T∈n表示關(guān)節(jié)位置;n是關(guān)節(jié)速度;n定義為關(guān)節(jié)加速度;Ni(ri)∈n×n表示對稱正定慣性矩陣;n×n表示科里奧利離心扭矩矩陣;Hi(ri)∈n是關(guān)節(jié)重力向量;ζi∈n表示控制輸入轉(zhuǎn)矩矢量;Γi(ri)∈n×n表示雅可比矩陣;Pi∈n是作用在第i個(gè)機(jī)械臂末端執(zhí)行器上的力矢量。
根據(jù)式(1),m個(gè)機(jī)械臂的動(dòng)力學(xué)方程為
(2)
其中,

Γ(r)=blockdiag[Γ1(r1),Γ2(r2),…,Γm(rm)]∈(mn)×(mn)N(r)=blockdiag[N1(r1),N2(r2),…,Nm(rm)]∈(mn)×(mn)

為了將機(jī)械臂系統(tǒng)與物體系統(tǒng)聯(lián)立,需引入物體動(dòng)力學(xué),其中被搬運(yùn)的物體動(dòng)力學(xué)[23]方程為
(3)
式中:xo∈n是物體的位置向量;和分別表示物體的速度與加速度;ξ∈n表示m個(gè)機(jī)械臂的組合力矢量;E∈n是來自未知環(huán)境的力矢量,作用于物體的中心;D(xo)∈n×n表示對稱正定慣性矩陣;n×n表示科里奧利離心矩陣;W(xo)∈n是重力矢量。
ξ和P之間的關(guān)系[23]為
ξ=JT(xo)P
(4)
其中,

式中:Ji(xo)是第i個(gè)機(jī)械臂末端執(zhí)行器和物體之間的雅可比矩陣;P可以分解為兩個(gè)正交分量,其表達(dá)式為
P=(JT(xo))+ξ+fI
(5)
式中:(JT(xo))+表示JT(xo)的偽逆矩陣,(JT(xo))+ξ是有助于物體運(yùn)動(dòng)的動(dòng)力矢量;fI指內(nèi)力矢量,其內(nèi)力誤差是有界的[23],fI在JT(xo)的零空間中滿足
JT(xo)fI=0
(6)
考慮被控物體和末端執(zhí)行器間可能會(huì)存在相對運(yùn)動(dòng)的情況,但在多機(jī)械臂搬運(yùn)物體過程中暫不考慮柔性的情況,因此得出以下假設(shè)。
假設(shè)1物體和末端執(zhí)行器之間不存在相對運(yùn)動(dòng),意味著末端執(zhí)行器在其工作場中剛性地接觸物體。
考慮到xi和ri之間的函數(shù)關(guān)系,其中xi表示第i個(gè)機(jī)械臂末端執(zhí)行器的位置,可得到第i個(gè)機(jī)械臂關(guān)節(jié)速度與末端執(zhí)行器速度之間的關(guān)系
(7)
類似地,第i個(gè)機(jī)械臂末端執(zhí)行器的速度和物體速度的表達(dá)式為
(8)
由式(7)和式(8)可以進(jìn)一步得到機(jī)械臂速度與物體速度之間的關(guān)系,表達(dá)式為
(9)
為了確保多機(jī)械臂工作在非奇異區(qū)域,需要假設(shè)Γi(ri)的逆矩陣存在,考慮到多個(gè)機(jī)械臂作用于一個(gè)物體,可以得到機(jī)械臂關(guān)節(jié)速度與加速度的表達(dá)式分別為
(10)
(11)
將式(10)和式(11)代入式(2),并與式(3)相結(jié)合,則機(jī)械臂與物體的總動(dòng)力學(xué)方程表達(dá)式為
(12)
其中,

由于不考慮外界環(huán)境力的影響,即式(12)中的Fe=0,物體的位置xo=[xo1,xo2,…,xoi]T受常數(shù)向量kb=[kb1,kb2,…,kbi]T約束,其中kbi>0,則滿足|xoi| 根據(jù)式(12),當(dāng)兩個(gè)機(jī)械臂協(xié)作搬運(yùn)同一物體時(shí),能夠按照給出的期望軌跡完成指定的動(dòng)作,被控物體在笛卡爾空間中跟蹤期望軌跡的示意圖如圖1所示。 圖1 兩個(gè)機(jī)械臂作用于一個(gè)物體的示意圖 性質(zhì)1式(12)中正定慣性矩陣M與C滿足[23] (13) 性質(zhì)2正定慣性矩陣M滿足 λmin(M)‖y‖2≤yTMy≤λmax(M)‖y‖2 (14) 時(shí),條件一致有界[23]。 式中:λmin(M)和λmax(M)分別對應(yīng)假定的兩個(gè)已知正常數(shù)的最小和最大特征值;‖*‖表示二范數(shù)。 在控制工程中,模糊邏輯系統(tǒng)通常用于逼近系統(tǒng)中的未知非線性函數(shù)。應(yīng)用模糊邏輯系統(tǒng)f的萬能逼近原理估計(jì)未知的連續(xù)函數(shù)f:s→,Z(t)=[Z1,Z2,…,Zs]T∈s,其中FLS是由IF-THEN規(guī)則構(gòu)造。如果Z1是是是則Y是El,其中:l=1,2,…,Q,Q表示模糊規(guī)則的條數(shù);Zi(1≤i≤s)是FLS的輸入;表示專家的語言變量。 在應(yīng)用單值模糊化器、乘積推理和中心平均解模糊器后,FLS估計(jì)未知非線性函數(shù)的值可以表示為 (15) (16) 為了提高逼近精度與逼近效率,設(shè)計(jì)了一種具有非零時(shí)變參數(shù)的FLS萬能逼近性質(zhì),由此得出引理1。 引理1在緊集U∈n中,對于任何給定具有李普希茲系數(shù)κi的連續(xù)未知函數(shù)Ψi(Z),存在一個(gè)FLSFi(Z)滿足表示近似誤差。然后在緊集中,β是由用戶提供的已知正常數(shù),則具有非零參數(shù)的萬能逼近不等式為 (17) (18) 從引理1的結(jié)果可知,通過應(yīng)用式(15)推導(dǎo)出式(16)的近似精度,表明FLS的輸出值可以通過未知非線性函數(shù)的非零時(shí)變參數(shù)ρ和李普希茲系數(shù)κi在線更新近似精度。 (19) 式中,x2=[x21,x22,…,x2n]T。 物體的期望軌跡表示為xd=[xd1,xd2,…,xdn]T,于是跟蹤誤差變量定義為 (20) 式中:z1=[z11,z12,…,z1n]T;z2=[z21,z22,…,z2n]T;c=[c1,c2,…,cn]T表示虛擬控制矢量,以確保跟蹤位置誤差z1可以收斂到一個(gè)以零為原點(diǎn)的鄰域內(nèi)。 考慮到物體位置x1的約束,并為了確保系統(tǒng)的穩(wěn)定性,選擇IBLF,其表達(dá)式為 (21) 引理2在{|x1i| (22) 對式(21)求導(dǎo),可以得到 (23) 其中, 式中,ci為虛擬控制器,其表達(dá)式為 (24) 式中,pi表示正控制增益。 (25) 由于|xdi| 將式(24)代入式(23),得到 (26) 為確保系統(tǒng)穩(wěn)定性,構(gòu)造新的IBLF,其表達(dá)式為 (27) 對式(27)求導(dǎo),可以得到 (28) (29) 將式(24)和式(29)代入式(28),并結(jié)合性質(zhì)1和性質(zhì)2,式(28)進(jìn)一步可以表示為 (30) 其中, 根據(jù)引理1的萬能逼近性,Ψ中的未知連續(xù)函數(shù)向量可以用模糊邏輯系統(tǒng)近似,則Ψ可以表示為 (31) 其中, κ=[κ1,κ2,…,κn]T ε=[ε1,ε2,…,εn]T Fo=O1×n (32) (33) (34) (35) 證明若滑模面選擇為 (36) (37) 通過式(37)可以實(shí)現(xiàn)定理1,證畢。 當(dāng)系統(tǒng)狀態(tài)到達(dá)滑模面s=0時(shí),意味著‖Z‖≤β|ρ|滿足。在這種情況下,可以得到‖z2‖≤β|ρ|,于是將模糊自適應(yīng)控制器和3個(gè)自適應(yīng)律分別設(shè)計(jì)為 (38) (39) (40) (41) 其中, 式中,參數(shù)γ,μ2,τi,η2i,λi和δ2i是由用戶給出的正常數(shù)。將式(31)和式(38)代入式(28),則可得 (42) 選擇如下IBLF,其表達(dá)式為 (43) 對V3微分,可得 (44) 考慮到不等式 (45) (46) 將式(45)和式(46)代入式(44)中,得到 (47) (48) 為確保跟蹤誤差收斂到一個(gè)以零為原點(diǎn)的零域內(nèi),則對式(48)積分,表達(dá)式為 (49) 由此可以得出定理2。 定理2如果同時(shí)滿足假設(shè)1和假設(shè)2,并在‖Z‖≤β|ρ|緊域上時(shí),所設(shè)計(jì)的自適應(yīng)律式(39)至式(41)和自適應(yīng)控制器式(38),可以確保多機(jī)械臂攜帶同一物體時(shí)的跟蹤誤差收斂到一個(gè)以零為原點(diǎn)的鄰域內(nèi)。同時(shí),保證閉環(huán)系統(tǒng)中的所有信號一致最終有界。 為了總結(jié)控制設(shè)計(jì)技術(shù),控制方案的穩(wěn)定性過程由定理3描述。 多機(jī)械臂系統(tǒng)包括兩個(gè)機(jī)械臂、一個(gè)物體和兩個(gè)機(jī)械臂末端執(zhí)行器上的力傳感器。 物體的期望軌跡選擇為 式中,t為期望軌跡的時(shí)間。 物體動(dòng)力學(xué)系統(tǒng)式(3)的參數(shù)為 式中:參數(shù)mo表示物體的重量;g表示重力加速度;mo=5 kg,g=9.8 m·s-2。 第i個(gè)機(jī)械臂的參數(shù)設(shè)置為 式中:Ni11=bi1+2bi2cos(ri2)+2bi3cos(ri3)+2bi4cos(ri2+ri3);Ni12=bi5+bi2cos(ri2)+2bi3cos(ri3)+bi4cos(ri2+ri3);Ni13=bi6+bi3cos(ri3)+bi4cos(ri2+ri3)Ni21=Ni12;Ni22=bi5+2bi3cos(ri3);Ni23=bi6+bi3cos(ri3);Ni31=Ni13; bi7cos(ri1)+bi8cos(ri1+ri2)+bi9cos(ri1+ri2+ri3);Hi2=bi8cos(ri1+ri2)+bi9cos(ri1+ri2+ri3);Hi3=bi9cos(ri1+ri2+ri3)。定義Ii=[bi1bi2bi3bi4bi5bi6bi7bi8bi9]T表示第i個(gè)機(jī)械臂的物理參數(shù),參數(shù)設(shè)置為I1=I2=[4.81 1.29 0.05 0.05 1.30 0.12 3.62 1.29 0.05]T。 第i個(gè)機(jī)械臂末端執(zhí)行器和關(guān)節(jié)的雅可比矩陣Γi(ri)的參數(shù)選擇為 式中:Γi11(ri)=-li1sin(ri1)-li2sin(ri1+ri2)-li3sin(ri1+ri2+ri3);Γi12(ri)=-li2sin(ri1+ri2)-li3sin(ri1+ri2+ri3);Γi13(ri)=-li3sin(ri1+ri2+ri3);Γi21(ri)=li1cos(ri1)+li2cos(ri1+ri2)+li3cos(ri1+ri2+ri3);Γi22(ri)=li2cos(ri1+ri2)+li3cos(ri1+ri2+ri3);Γi23(ri)=li3cos(ri1+ri2+ri3);Γi31(ri)=Γi32(ri)=Γi33(ri)=1。參數(shù)li1、li2和li3分別表示第i個(gè)機(jī)械臂的連桿1、連桿2和連桿3的長度(i=1,2),其中l(wèi)11=l21=2 m,l12=l22=1.5 m,l13=l23=0.5 m。 第i個(gè)機(jī)械臂末端執(zhí)行器和被抓取物體的雅可比矩陣Ji(xo)選擇為 式中,lio是第i個(gè)機(jī)械臂末端執(zhí)行器到物體質(zhì)量中心的長度,lio的實(shí)際值為l1o=l2o=0.5 m。 為補(bǔ)償未知非線性函數(shù)Ψi,選擇語言變量的域?yàn)?/p> 式中,r=1,2,…,18是第r個(gè)狀態(tài)變量,標(biāo)記負(fù)大(Negative Big,NB)、負(fù)中(Negative Middle,NM)、負(fù)小(Negative Small,NS)、負(fù)零(Negative Zero,NZ)、正零(Positive Zero,PZ)、正小(Positive Small,PS)、正中(Positive Middle,PM)和正大(Positive Big,PB)表示語言變量。 圖2 位置跟蹤軌跡的3種方法 圖3 3種方法的跟蹤誤差 由圖2和圖3可以看出,模糊自適應(yīng)控制的位置跟蹤速度最快,逼近誤差更小,并且位置跟蹤誤差可以收斂到以零為原點(diǎn)的鄰域內(nèi)。在未違反輸出約束條件下物體沿著期望信號運(yùn)動(dòng)過程中,可以看出模糊自適應(yīng)控制的跟蹤軌跡與跟蹤誤差效果優(yōu)于自適應(yīng)控制與模糊PD控制。 為了說明模糊自適應(yīng)控制中的自適應(yīng)律較少,將模糊自適應(yīng)控制中的自適應(yīng)律與模糊PD控制中的自適應(yīng)律進(jìn)行比較,具體分別如圖4和圖5所示。 圖4 模糊PD控制中的自適應(yīng)律 圖5 模糊自適應(yīng)控制中的自適應(yīng)律 由圖4和圖5中可以看出,模糊自適應(yīng)控制相較于模糊PD控制而言,具有較少的自適應(yīng)律,且能夠提高計(jì)算效率。 為了更清楚地體現(xiàn)出模糊自適應(yīng)控制具有精準(zhǔn)的跟蹤效果,對物體在笛卡爾空間中跟蹤期望軌跡進(jìn)行分析,具體如圖6所示。由圖6可以看出,在笛卡爾空間中,物體在跟蹤理想軌跡xd運(yùn)動(dòng)時(shí)具有較好的跟蹤效果。 圖6 在笛卡爾空間中物體的運(yùn)動(dòng)軌跡 關(guān)于模糊自適應(yīng)控制中的速度跟蹤響應(yīng)及跟蹤誤差的情況具體如圖7和圖8所示。由圖7和圖8可以看出,模糊自適應(yīng)控制具有穩(wěn)定的速度跟蹤性能,并且跟蹤誤差能夠收斂到以零為原點(diǎn)的鄰域內(nèi)。在多機(jī)械臂攜帶物體運(yùn)動(dòng)的過程中,通過系統(tǒng)施加在物體上控制扭矩的大小確保模糊自適應(yīng)控制器Fo的有效性,具體如圖9所示。由圖9可以看出,系統(tǒng)施加于物體的控制扭矩是平滑且有界的,并能夠在短時(shí)間內(nèi)穩(wěn)定到一個(gè)相對較小的范圍中,因此所提的模糊自適應(yīng)控制器Fo是有效的。 圖7 模糊自適應(yīng)控制中的速度跟蹤響應(yīng) 圖8 跟蹤誤差 圖9 系統(tǒng)施加于物體的控制扭矩 針對具有未知?jiǎng)恿W(xué)和輸出約束的多機(jī)械臂系統(tǒng),設(shè)計(jì)了一種基于逼近精度和李普希茲系數(shù)的自適應(yīng)模糊邏輯系統(tǒng)控制器。首先,通過對FLS系統(tǒng)的萬能逼近原理引入了一個(gè)非零參數(shù)來逼近非線性函數(shù)。其次,利用IBLF的穩(wěn)定性原理設(shè)計(jì)的控制器與自適應(yīng)律保證了系統(tǒng)在FLS逼近域內(nèi)時(shí)的穩(wěn)定性,針對系統(tǒng)狀態(tài)在FLS域外時(shí)的情況,通過滑模控制的方法將狀態(tài)拉回到FLS域內(nèi)。最后,將所設(shè)計(jì)的模糊自適應(yīng)控制器與自適應(yīng)控制器和模糊PD控制器進(jìn)行仿真對比。仿真結(jié)果表明,與這兩種控制器相比,所提出的控制器可以確保在不違反輸出約束的情況下,具有良好的跟蹤性能,同時(shí)能在線更新自適應(yīng)律,并且閉環(huán)系統(tǒng)中的所有信號均滿足一致最終有界。



1.2 FLS系統(tǒng)




2 具有輸出約束的控制器




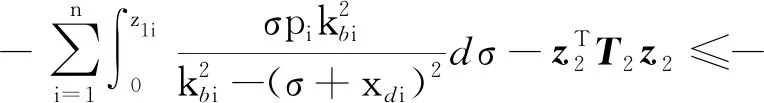














3 仿真結(jié)果及分析














4 結(jié)語

