數據采集系統輸入電阻的不確定度分析與評定

梁志國，馮秀娟

（1.航空工業北京長城計量測試技術研究所 計量與校準技術重點實驗室，北京100095；2.中國計量科學研究院 力學與聲學計量科學研究所，北京100029）

0 引言

電壓類測量儀器的測量原理簡言之是將其并聯入被測對象的電路之中，測量并獲取被測對象的電壓。因而，輸入阻抗是非常重要的性能指標。在輸入阻抗中，電阻分量居主導地位，電抗分量往往非常微小，可以忽略，故多數情況下的輸入阻抗測量是指輸入電阻的量值測量，尤其是高阻狀態。

通常，電壓類測量儀器的設計應用遵循兩種不同理念，一種為高阻設計理念，主要用于100 MHz 及以下的中低頻率范圍，以集總參數元器件為核心的電路理論為基礎的儀器儀表；相比于被測量對象的內阻，測量儀表的輸入電阻特別巨大，在測量過程中，給被測對象帶來的影響很微小，可以忽略不計，例如數字電壓表［1］、100 MHz 及以下帶寬的示波器。另外一種為匹配設計理念，輸入電阻（輸入阻抗）通常為50 Ω；主要用于中高頻率及以上的頻率范圍，以分布參數效應元器件為核心的電磁場理論為基礎的儀器儀表，如瞬態波形記錄儀，寬帶示波器等等［2］。相比于所測對象，其阻抗具有相同的量值，因而在較低頻率情況下，能從被測對象處獲取最大的信號功率，而在較高頻率情況下，對被測對象造成的電能量反射最少。

直流以及中低頻率測量儀器多采用高阻設計，而射頻及微波頻率范圍測量儀器全部采用匹配設計方案。數據采集系統多數屬于中低頻率測量范疇，通常使用高阻輸入的設計方案。但仍然有少數稱為高速數據采集系統的儀器，其模擬帶寬可達100 MHz以上，使用了匹配設計模式，并且具有直流耦合和交流耦合兩種不同的耦合方式。

輸入阻抗測量可使用RLC 測量儀、交流電橋等儀器直接測量，并以某種簡單的等效電路形式給出其參數，如電阻與電容并聯形式分別給出電阻和電容值，電阻與電感串聯形式分別給出電阻和電感值；也可使用阻抗分析儀、矢量網絡分析儀、時域反射計等儀器分析獲得［3-4］。

通常，匹配傳輸設計的輸入電路使用阻抗參數表征［5-7］。高阻傳輸設計的輸入電路主要使用輸入電阻參數表征［8-13］。由于阻抗會隨頻率不同而變化，但輸入電阻則具有相對的穩定性與一致性，故在高阻抗電路中常被作為測量對象［14-19］。同時，針對輸入電阻測量的改進研究也曾經不斷涌現［20-22］，其中包括輸入電阻帶來的誤差影響［23-27］。

本文主要討論數據采集系統輸入電阻計量校準中的問題及其不確定度評定。

1 測量原理與方法

數據采集系統輸入電阻測量原理為歐姆定律［28］。如圖1 所示接線，選擇標準電阻R為與數據采集系統輸入電阻標稱量值Ri相當的值（一般為（0.1 ～ 10）Ri），將被校采集通道通過標準電阻R接到直流電壓信號源上。

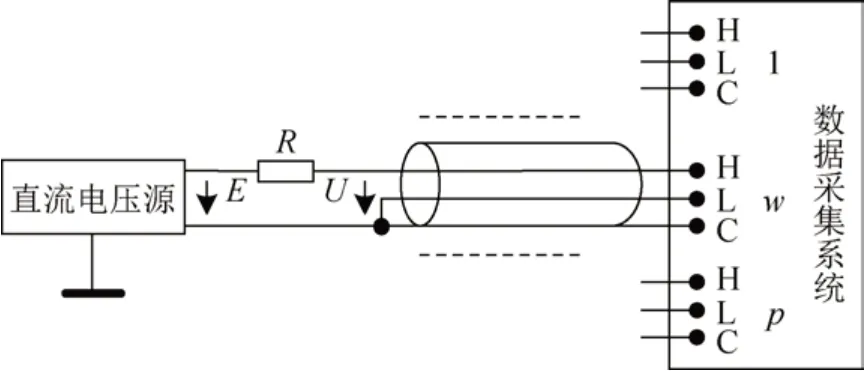
圖1 校準輸入電阻的接線圖Fig 1 Input resistance calibration diagram

設置直流電壓源信號幅度E=E1，加載信號，啟動采集，記錄采集數據x1j，（j= 0，…，n-1），折合到輸入端的測量幅度值U1為

式中：n為每個通道采集數據個數；G0為測量通道的增益值。

將信號幅度調置為E=E2，加載信號，啟動采集，記錄采集數據x2j，（j= 0，…，n-1），折合到輸入端的測量幅度值U2為

按式（3）計算數據采集系統通道輸入電阻Rin。

其中，E1、E2的選取原則是使得對應的測量值U1、U2兩者之差越大越好，從而降低輸入電阻的測量不確定度。

2 測量不確定度模型

由式（3）可見，輸入電阻Rin與信號幅度E1、E2、U1、U2以及標準電阻R均有關，因此，可以列出輸入電阻Rin測量不確定度的主要來源為：①信號幅度E1、E2之差ΔE0的不確定度u（ΔE0），主要由標準信號源的誤差造成；②信號幅度U1、U2之差ΔU0的不確定度u（ΔU0），主要由標準信號源的誤差和測量系統自身造成；③標準電阻R的測量不確定度u（R），主要由標準電阻R的誤差等因素造成。

由式（3）可得

靈敏系數為

測量過程中，假設輸入電阻Rin測量不確定度的不同分量之間不相關，根據輸出測量值對于輸入量的測量值的不確定度傳遞公式［29］，由式（8）獲得其合成標準不確定度uc（Rin）為

由式（9）獲得其相對合成標準不確定度urel（Rin）為

由式（15）可見，輸入電阻測量不確定度為標準直流電壓ΔE0不確定度、測量電壓ΔU0不確定度和標準電阻R不確定度的合成，其傳遞系數c0則由輸入電阻與標準電阻的比值Rin/R確定，為降低其測量不確定度，除了標準直流電壓源的不確定度和標準電阻的不確定度要求外，需要選取輸入電阻與標準電阻的比值（Rin/R）足夠小，通常要求R≥Rin。

3 測量數據及處理

選取NI USB-4431型數據采集系統作為被測對象［30］，共有4個差分輸入通道，量程范圍為±10 V，24 位A/D，最大允許誤差為±0.15%，采集速率1 ～102.4 kSa/s，標稱輸入電阻200 kΩ。選取通道1作為測量通道，其通道增益標定為G0= 1.002 857。

以9500B 型示波器校準儀作為直流電壓標準源［31］，幅度范圍為±（10 mV ～ 10 V），最大允許誤差為±0.03% ～ ±0.001%。選標準電阻R= 200 kΩ，最大允許誤差±0.01%，誤差在［-0.01%，+0.01%］范圍內服從均勻分布，相對不確定度為

給數據采集系統通道1 分別加載E1= 7.000 V，E2= 9.000 V，設置采集數據個數n= 100。獲得采集測量結果，用式（1）、（2）計算得U1、U2，用式（3）計算得輸入電阻Rin，如表1所示。

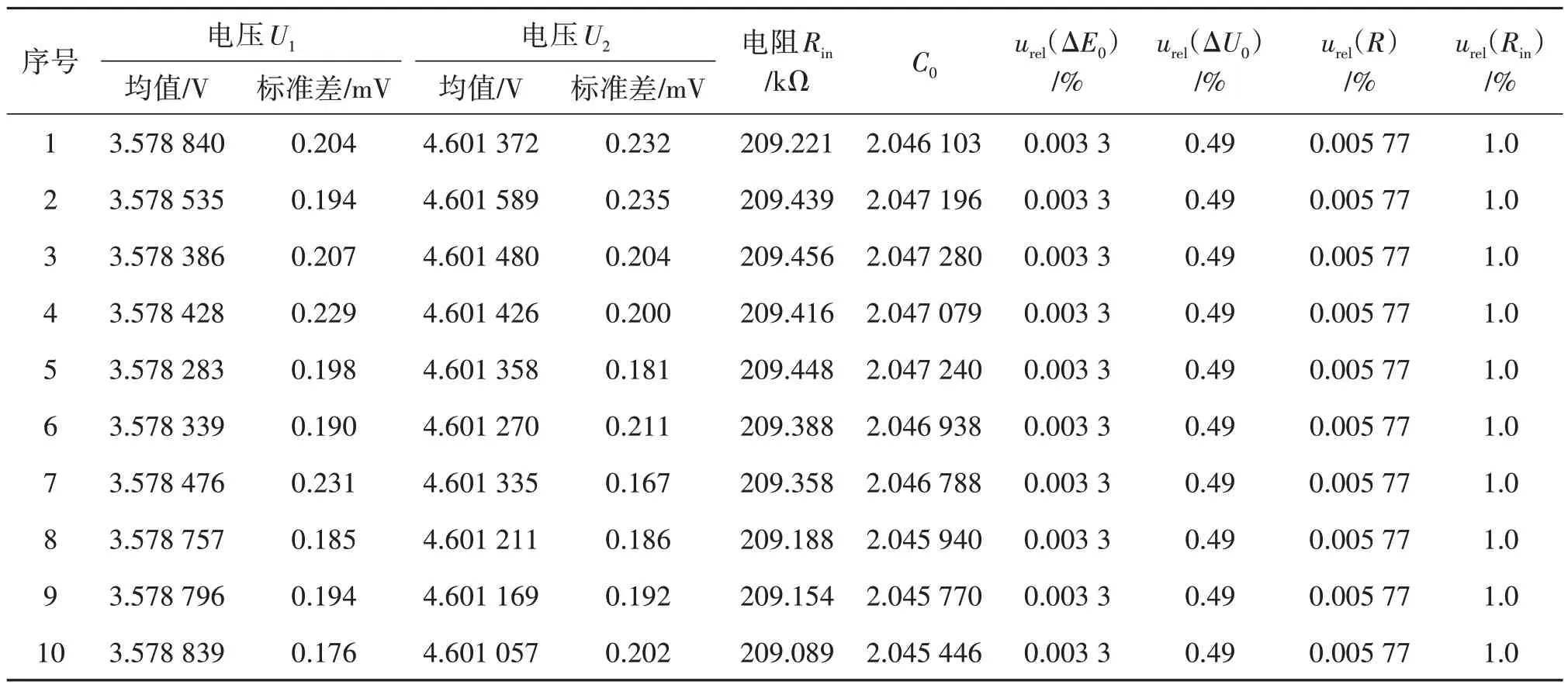
表1 輸入電阻測量結果Tab.1 Input resistance measurement results

按照直流標準源9 500B 的指標，設E1和E2的最大相對誤差均為±0.001%，并假設均服從均勻分布。則，

E1的最大允許誤差為

E1的不確定度為

E2的最大允許誤差為

E2的不確定度為

ΔE0=E2-E1的不確定度為

按照數據采集系統NI USB-4431的指標，設U1和U2的最大相對誤差均為±0.15%，并假設均服從均勻分布。則

U1的最大允許誤差為

U1的不確定度為

U2的最大允許誤差為

U2的不確定度為

ΔU0=U2-U1的不確定度為

計算結果如表1所示。

4 合成不確定度

通過式（13）計算靈敏系數，按照式（15）計算合成標準不確定度相對值urel（Rin），如表1所示。

從輸入電阻Rin的10 次測量結果可見，實驗標準偏差為0.14 kΩ，與輸入電阻之比為0.067%，與urel（ΔU0）相比，可以被忽略。因此，Rin測量重復性造成的不確定度可以忽略，從單次測量獲得的結果及不確定度可以完整表征Rin的測量。

5 擴展不確定度及測量結果

將表1 中各個不確定度分量集中列出，如表2所示。

表2 不確定度分量概算表Tab.2 Estimation table of uncertainty components

從表2 中各個不確定度分量的量值水平來看，存在主導分量urel（ΔU0），其量值水平占據主導地位且量值服從梯形分布，由此可認定，合成標準不確定度相對值urel（Rin）近似服從梯形分布。

由于U1的誤差在區間［-ΔU1，ΔU1］ = ［-5.37 mV，+5.37 mV］內服從均勻分布，U2的誤差在區間［-ΔU2，ΔU2］= ［-6.90 mV，+6.90 mV］內服從均勻分布，則其差值ΔU0=U2-U1應服從梯形分布，其上下底之比為

取置信概率p= 95%，則有包含因子［32］

k95= 1.89，則擴展不確定度為

數據采集系統的輸入電阻為

其中，“±”后面是輸入電阻的擴展不確定度，包含因子k95= 1.89，是由梯形分布假設以及置信概率p= 95%的要求計算獲得。

6 結論

輸入電阻的測量不確定度主要來自標準電壓源、輸入端測量電壓和標準電阻的合成結果。實際工作中輸入電阻的不確定度往往非常大，不知緣故。

輸入電阻的相對不確定度為ΔE0的不確定度u（ΔE0）和ΔU0的不確定度u（ΔU0）以及標準電阻R的測量不確定度u（R）的加權合成，權值c0則由輸入電阻與標準電阻的比值Rin/R確定。此比值不宜過大或過小，過小時，電位差的不確定度變大，過大時，權值變大，產生不確定度的放大效果。因此，Rin/R量值在1附近為較佳選擇。

在本組實驗的條件下，數據采集系統的測量誤差占主導地位。若想降低輸入電阻的測量不確定度，除了平衡標準電阻、輸入幅度E1和E2和測量幅度U1和U2等各個物理量不確定度的貢獻，從而尋求最佳狀態以外，還可以使用高精度數字電壓表來替代數據采集系統測量獲得U1和U2，以降低輸入電阻的測量不確定度，即通過選取電壓源、標準電阻以及測量電壓的方式控制測量結果的不確定度。

在實際工作中，使用數字電壓表進行測量還應考慮其輸入電阻對被測電路帶來的額外負載效應的影響。