數學教學中從幾何空間創新理解向量數量積

胡 乙

(江蘇經貿職業技術學院,江蘇 南京 211168)

在數學中,向量數量積(內積或點積)指:兩個向量a和b的模與它們夾角余弦的乘積[1].向量夾角與數量積教學一直是向量教學的重點與難點.在教學實踐中,如何引導學生完整準確地理解以上概念,中外學界對此一直未達成共識.

目前國內教材普遍運用物理學中恒力F做功的公式說明向量數量積概念,而從數學幾何出發講授向量數量積,其研究尚處于萌芽狀態.程仕然認為從物理學恒力F做功公式推導向量數量積公式有以下不足:一是學生尚不完全熟悉物理做功公式,二是物理學公式與數學公式描述的符號及說法上有不同,可能造成學生新的困擾[2].據此,教師如果轉換思路,從求解向量夾角入手推導向量數量積公式,則可能彌補以上不足.陳文雅、江一鳴主張:將向量視為線段,從線段投影出發,運用數形結合思想,將向量數量積視為向量間投影[3].可見,若從幾何空間出發設計向量相關教學,則師生教學可能更為輕松.

國外學界傾向于從幾何空間出發,首先從笛卡爾坐標定義向量數量積,再運用向量封閉回路法構造直角三角形證明向量數量積公式.如卡爾·P.西蒙等提出應在幾何空間中運用封閉回路構造直角三角形,并運用勾股定理推導向量數量積公式[4].此觀點已經涉及向量數量積的數學本質,但不完整.完整的向量數量積教學應包含兩方面,即從向量坐標法與向量封閉回路法出發,全面講授向量數量積概念.

此外,通過調整相關概念教學順序,可能會提高教學效率.按觀察問題、解決問題的邏輯順序,學生應首先認識向量夾角,在計算向量夾角大小的過程中,教師可引導學生歸納出求解向量夾角余弦值的算法,對算法做適當變換后,再引導學生學習向量數量積概念.以上教學設計不僅有利于學生深入理解向量數量積的數學本質,而且可培養學生在解決實際問題中進行數學抽象的能力.

據此,研究擬從數學幾何出發,首先引導學生發現笛卡爾平面中的向量夾角,并從向量坐標法與向量封閉回路法兩種角度引導學生求解向量夾角余弦值,在此過程中,啟發學生歸納出求解向量夾角余弦值的公式,對公式做適當變換后,教師可正式提出向量數量積概念.同時,因為向量是溝通幾何與代數的橋梁,為使學生深入理解以上概念,研究將從向量坐標與封閉回路兩個角度,引導學生運用向量數量積公式,創新證明歐氏幾何直角三角形相關定理,使學生從多角度深入認識向量的概念與作用,并學會在數學、物理學、經濟學等不同學科中,主動運用以上知識分析相關數學模型,以此激發學生的學習興趣,實現教學初衷.

1 向量夾角與向量數量積

與傳統教學不同,教師可在笛卡爾平面建立向量夾角,請學生運用三角函數計算該夾角的余弦值,在此過程中,引導學生推導向量數量積公式.待學生熟練掌握后,教師可從向量封閉回路角度再次引導學生理解向量夾角與向量數量積.

1.1 從向量坐標法理解向量夾角與向量數量積

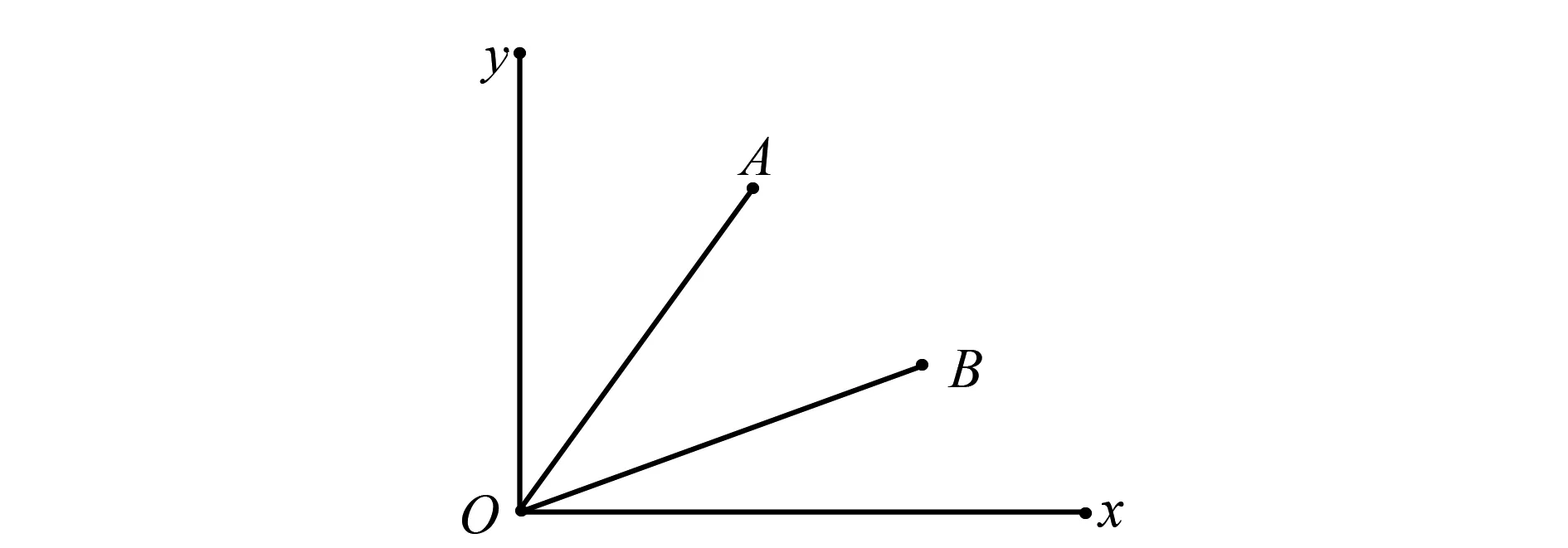
圖1 從向量數對(坐標)出發理解向量夾角與向量數量積

cos∠AOB=cos(∠AOX-∠BOX)

=cos∠AOXcos∠BOX+sin∠AOXsin∠BOX

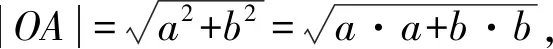
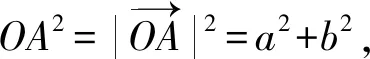
從幾何空間出發求解向量夾角時,當學生將兩向量起點均平移至原點后,則可通過兩向量終點坐標求解向量夾角余弦值,從以上計算過程中定義向量數量積,則學生可能更為容易接受,且更能體會到向量的數學本質.

1.2 從封閉回路理解向量夾角與向量數量積

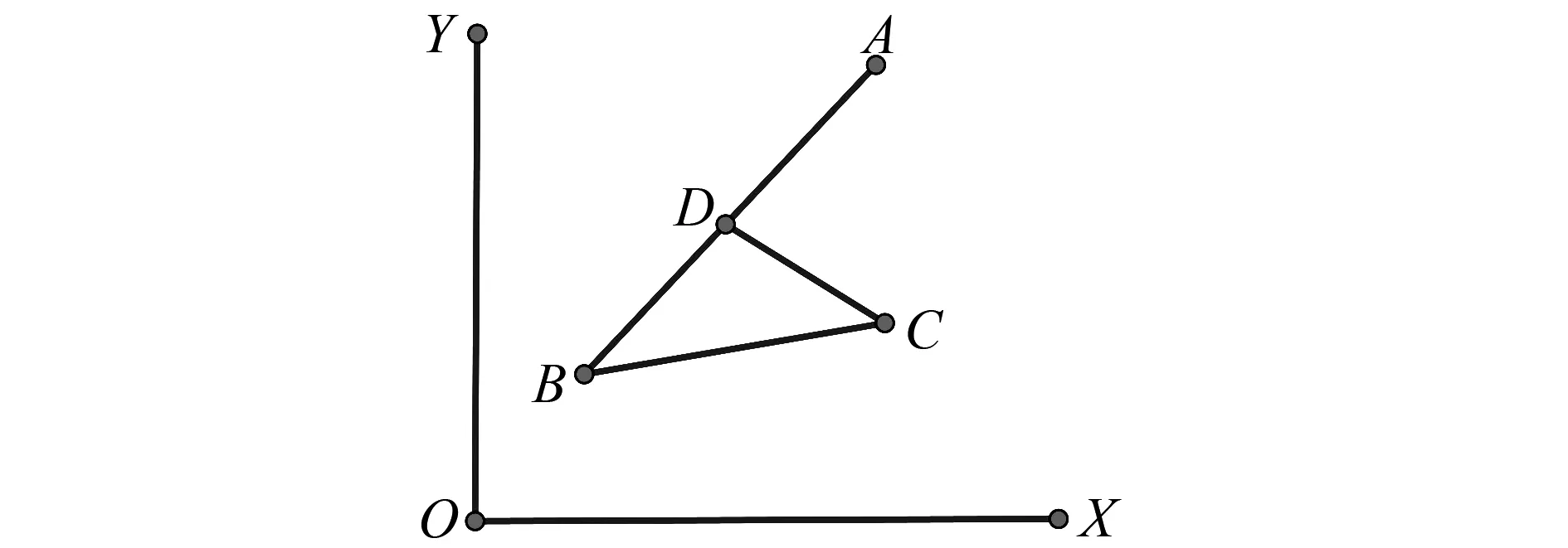
圖2 從封閉回路法出發理解向量夾角與向量數量積

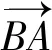
又根據勾股定理,

聯立以上三式,展開得:

整理得:

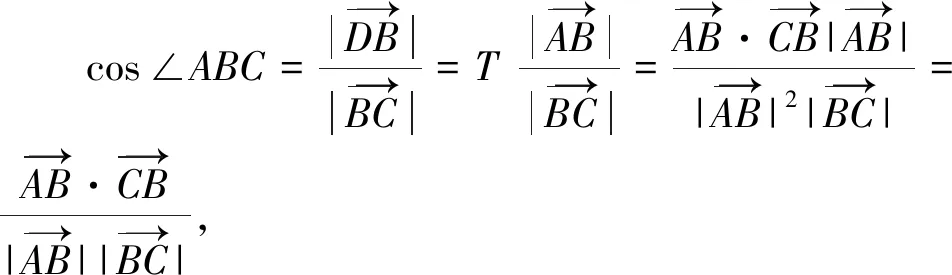
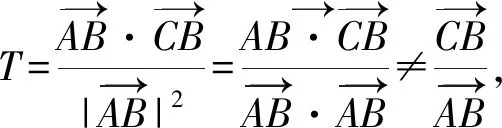
據此,教師可總結向量夾角cosθ的重要性質:當θ為銳角時,cosθ>0;為鈍角時,cosθ<0;為直角時,cosθ=0;為零度時,cosθ=1.綜上,一般情況下,-1≤cosθ≤1.特別的,當需要證明直線或者線段間夾角為直角時,除了運用綜合證明方法外,學生可嘗試運用向量數量積求證.此外,在歐氏幾何教學中,教師可引導學生嘗試運用向量求解相關試題.例如:如果不在同一平面的兩線段向量數量積為零,則學生可證明其相互垂直等.學生運用向量求解幾何問題,在一定程度上可避免背誦繁瑣的定理,同時在解題時可不加或少加輔助線,如此則有利于減輕學生學習負擔,激發學生學習興趣.

2 向量數量積與歐氏直角三角形相關定理的證明

張景中主張運用向量數量積求解或者求證度量幾何中垂直、角度值、異面線段長度比值等難題[5].依據試題條件,教師可引導學生從向量坐標法與向量封閉回路法求解相關幾何試題.以直角三角形相關定理證明為例,相較于綜合證明方法,向量數量積方法則更加簡潔高效.

1.3 向量數量積與勾股定理

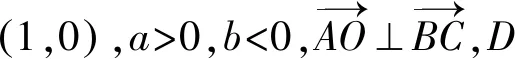
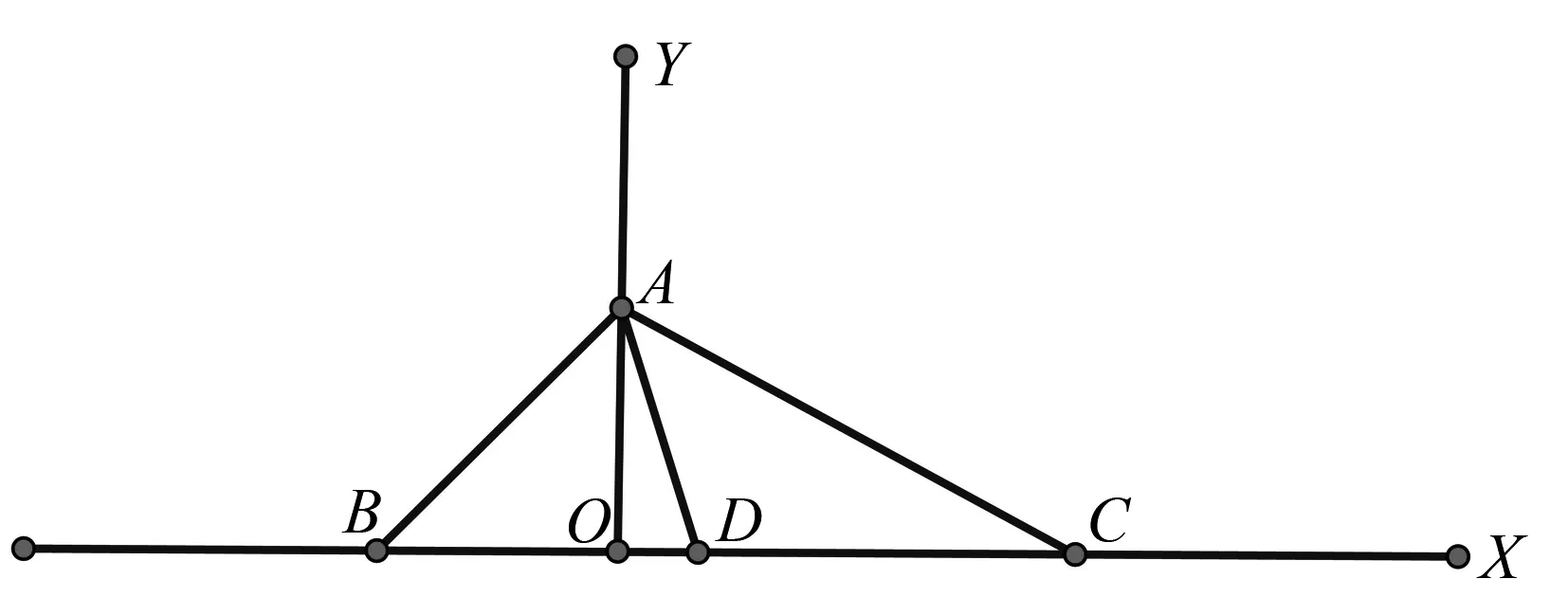
圖3 笛卡爾平面中直角三角形的高與中線

a2=-b,b<0,

故AB2+AC2=BC2.

從向量封閉回路法出發,省略繁瑣的坐標,學生運用向量數量積公式可直接得到勾股定理.

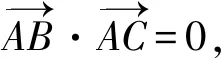
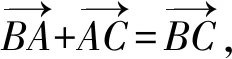
AB2+AC2=BC2.

同理,學生可從向量坐標法證明勾股定理逆定理:

如圖3,A點坐標(0,a),B點坐標(b,0),C點坐標(1,0),a>0,b<0,設AB2+AC2=BC2,求證∠BAC為直角.

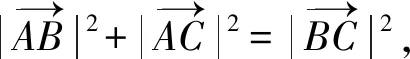
則b2+a2+a2+1=1+b2-2b,

得a2=-b,a>0,b<0,

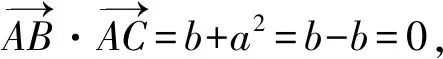
故∠BAC為直角.

與向量坐標法不同,學生運用向量封閉回路證明勾股定理、余弦定理等則更為簡潔自然,且幾乎不用添加輔助線或構造圖形,教師可運用三角形封閉回路性質,再次展示如何證明余弦定理與勾股定理逆定理.

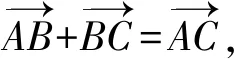
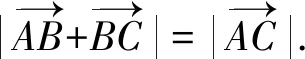
因為結論涉及平方,故對等式兩邊平方,并運用數量積公式可推理得到等式 :

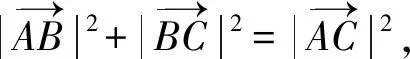
教師僅僅運用向量封閉回路、全程未添加輔助線即完成證明.據此,教師可嘗試引導學生用向量知識重新證明幾何、代數中相關定理,為學生學習提供新思路,并在此過程中加深學生對向量的理解.

1.4 向量數量積與直角三角形射影定理

用向量證明直角三角形射影定理將更為簡潔,如圖3,直角ΔBAC中,AO⊥BC,請學生證明:AB2=BO·BC,AC2=CO·CB,AO2=BO·OC.

運用原有坐標,學生可構造如下向量:

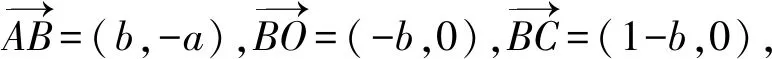
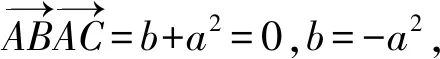
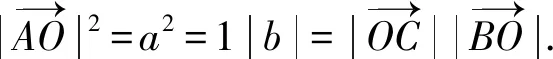
以圖3為例,學生可運用向量封閉回路法再次證明直角三角形射影定理.證明的關鍵是,學生能將已知向量分解為合適的封閉向量,并能運用數量積為零的條件消除無關向量.

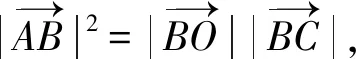
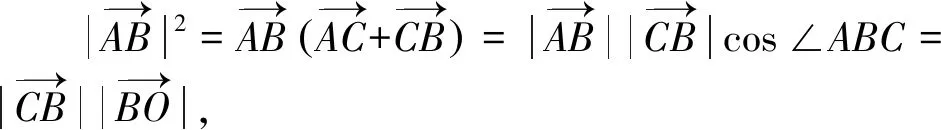
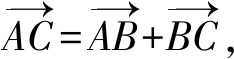
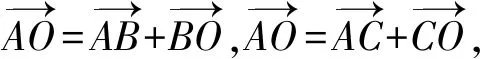
2 總結

從數學幾何出發,教師可首先指導學生計算向量間夾角數值,在此過程中,引導學生推導向量數量積公式.教師應從向量坐標法與向量封閉回路法兩種角度完整講授向量夾角與向量數量積.運用向量數量積,學生可創新證明歐式幾何中相關定理.限于篇幅,本研究并未詳細闡述向量數量積在立體幾何、解析幾何、不等式等教學內容中的應用.未來教學中,教師可嘗試運用質點幾何法講授向量數量積及相關向量知識.