2022年全國乙卷理科第11題的解法研究與修正建議

曾吉相

(遵義市第四中學,貴州 遵義563000)

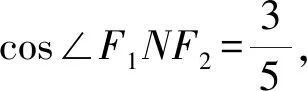
1 試題分析

本題以直線與雙曲線的位置關系作為情境,考查圓錐曲線離心率的求解.結合圖形,利用正(余)弦定理結合三角變換、雙曲線的定義與性質,得到a,b,c之間的關系即可求解.注意討論點M,N在雙曲線的同一支或者在各一支的情況.因為最終的結果是有兩種情況,故建議該題修正為多選題或者兩個正確選項中只要考生選對一個都給分.

2 解法探究

思路1正弦定理,轉化關系.

解法1不妨設雙曲線焦點在x軸,設過點F1作圓D的切線切點為G.

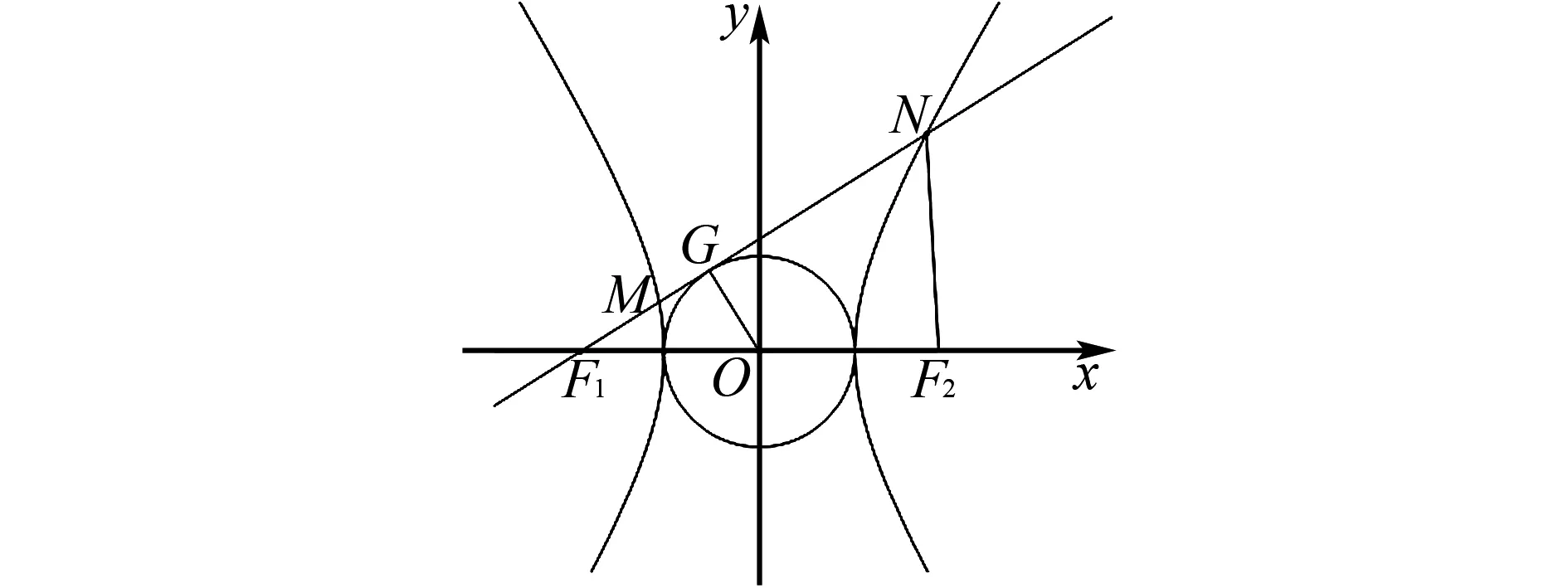
圖1 點M,N分別在雙曲線左右支

又|OG|=a,|OF1|=c,|GF1|=b,設∠F1NF2=α,∠F2F1N=β,在△F1NF2中,有

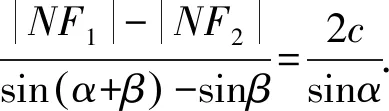
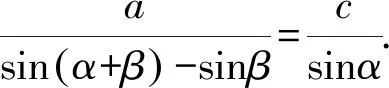
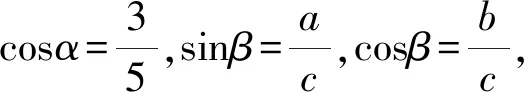
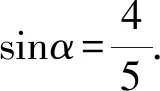
代入整理得到2b=3a.

所以雙曲線的離心率

②若M,N均在左支上,如圖2所示,同理有

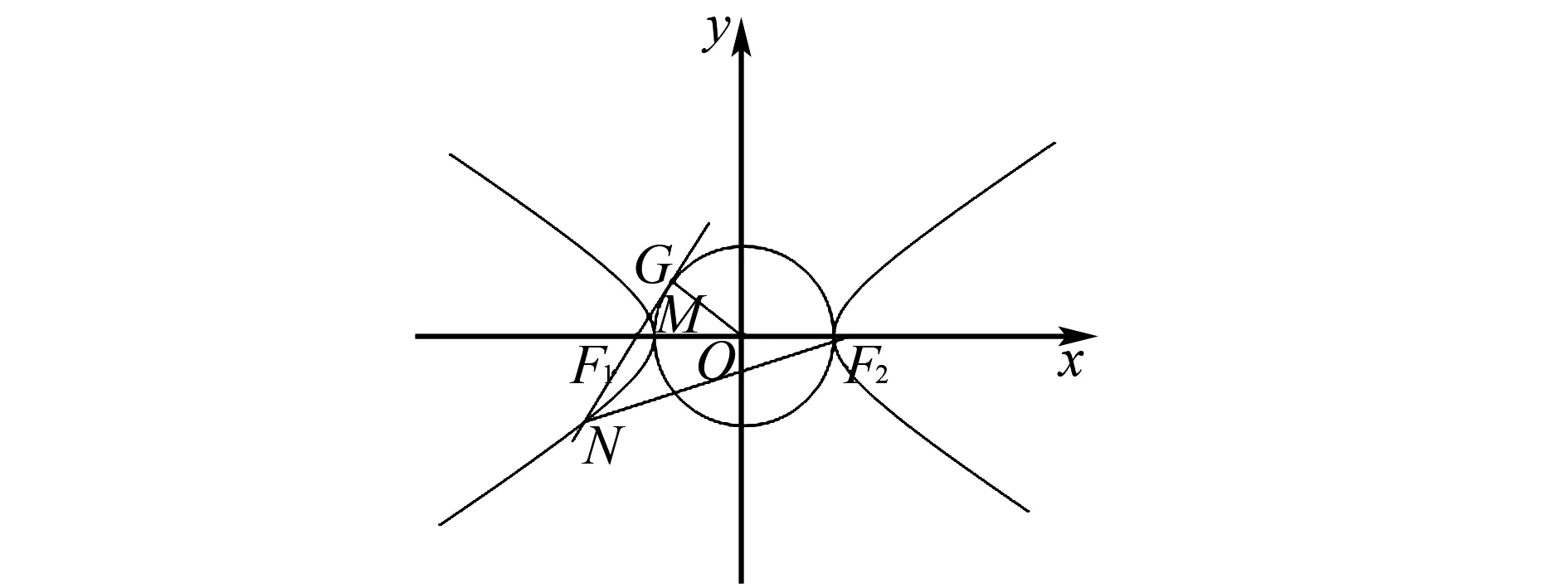
圖2 點M,N均在雙曲線左支上

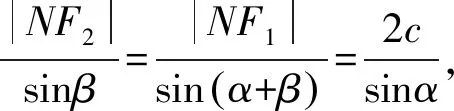
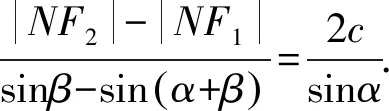
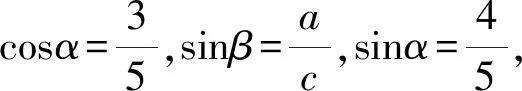
故a=2b.

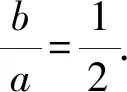
綜上所述,選AC.

思路2正弦、余弦雙管齊下.

解法2 (以點M,N分別在左右兩支為例)不妨設雙曲線的焦點在x軸上,則以雙曲線的實軸為直徑的圓即為圓O,如圖1所示.

記雙曲線C的實軸長為2a,虛軸長為2b,焦距為2c,切線與圓O的切點為G,連接OG,則

OG⊥NF1.

在Rt△GOF1中,|OG|=a,|OF1|=c,則

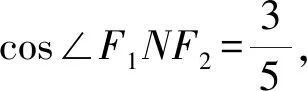
在△NF1F2中,由正弦定理,得

在△NF1F2中,由余弦定理,得

|F1F2|2=|NF1|2+|NF2|2-2|NF1||NF2|·cos∠F1NF2.

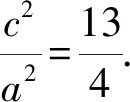
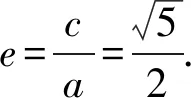
綜上所述,選AC.

思路3巧作垂線,化斜為直.

解法3 (以點M,N分別在左右兩支為例)不妨設雙曲線的焦點在x軸上,則以雙曲線的實軸為直徑的圓即為圓O,如圖3所示.

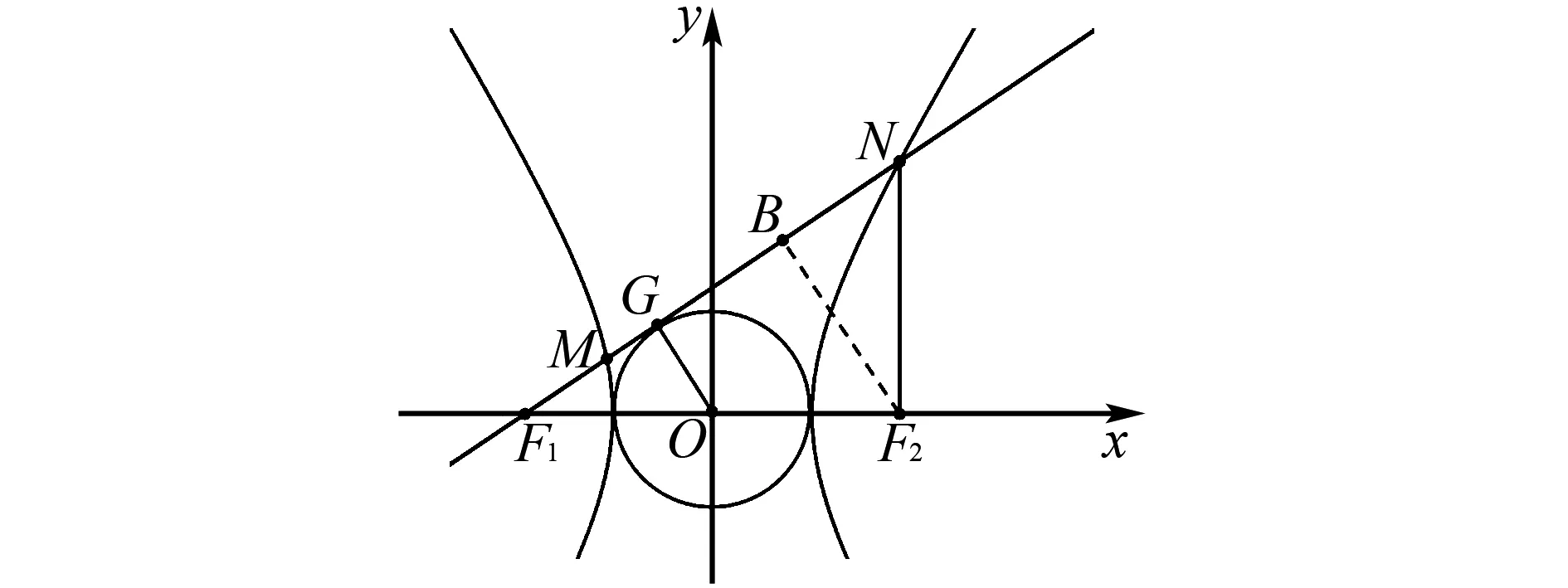
圖3 解法3示意圖

記雙曲線C的實軸長為2a,虛軸長為2b,焦距為2c,則

|NF1|-|NF2|=2a,|F1F2|=2c.

設切線與圓O的切點為G,連接OG,過點F2作F2B⊥NF1于點B,則OG∥F2B,且G為F1B的中點.

由條件|OG|=a,則

|BF2|=2a,

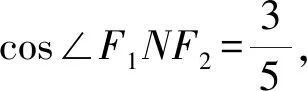
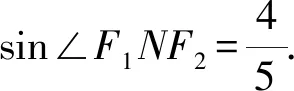
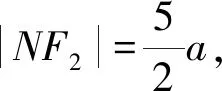
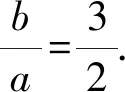
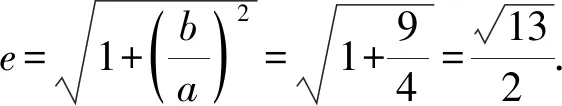
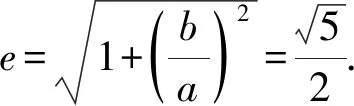
綜上所述,選AC.

思路4小題小做,巧取特值.

解法4(以點M,N分別在左右兩支為例)不妨設雙曲線的焦點在x軸上,則以雙曲線的實軸為直徑的圓即為圓O.記雙曲線C的實軸長為2a,虛軸長為2b,焦距為2c.

設切線與圓O的切點為G,連接OG,過點F2作F2B⊥NF1于點B,則OG∥F2B,且G為F1B的中點.

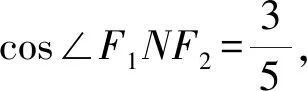
所以|OG|=a=2,

|NF1|=|NF2|+2a=9,|BF1|=9-3=6.

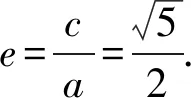
綜上所述,選AC.

3 題后反思

解法3和4通過作垂線,在關聯情境中,想象并構建相應問題的幾何圖形,化斜三角形為直角三角形,有利于問題的解決.需要考生借助圖形提出數學問題,發現圖形與圖形、圖形與數量的關系,解決實際數學問題.

4 背景推廣

證明在△PF1F2中,由正弦定理,得

由等比定理,得

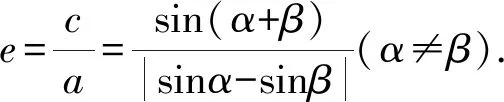
證明在△PF1F2中,由正弦定理,得

由等比定理,得

5 變式訓練

答案提示:D;C.