正態分布定數和定時截尾數據可靠性評估方法
傅惠民, 郭建超, 付越帥, 李子昂
(北京航空航天大學 小樣本技術研究中心, 北京 100191)
0 引言
隨著產品質量和可靠性越來越高, 產品壽命越來越長,導致壽命試驗所需時間長、費用高,工程上難以承受。因此, 定數和定時截尾壽命試驗目前已成為工程上一類常用的壽命試驗[1]。定數截尾壽命試驗是試驗達到事先規定的失效數時停止試驗,此時試驗停止時間是隨機變量;定時截尾壽命試驗則是試驗達到事先規定的時間停止試驗,此時得到的失效數為隨機變量。 定數和定時截尾壽命試驗數據都不是傳統的完全壽命數據, 在統計分析上比較復雜。
由于指數分布具有簡單的數學形式和性質, 其推導和計算都相對容易,所以人們對于產品壽命遵循指數分布情況, 已經建立了能夠根據定數和定時截尾壽命試驗數據進行可靠性評估的方法, 并廣泛應用于工程實踐中[2]。但是, 對于工程上常見的產品對數壽命遵循正態分布的情況, 還難以根據定數和定時截尾壽命試驗數據進行可靠性評估。 鑒于工程上許多情況產品對數壽命標準差均為已知[3],因此本文在文獻[4-5]給出的不完全壽命數據可靠性評估方法的基礎上, 進一步建立了一種正態分布定數和定時截尾數據可靠性評估方法, 能夠根據定數或定時截尾壽命試驗數據給出產品高置信水平、 高可靠度的可靠壽命單側置信限或可靠度單側置信下限, 從而使工程上許多原先無法處理的定數或定時截尾壽命試驗數據得以統計分析,實現小樣本可靠性評估。
1 正態分布定數截尾數據可靠性評估
定數截尾試驗是工程上一類常見的重要試驗, 它要求試驗達到事先規定的失效數時停止試驗。 下面給出產品對數壽命遵循正態分布情況下的定數截尾數據可靠性評估方法。
1.1 定數截尾數據可靠壽命評估方法
設某產品對數壽命X=lgN 遵循標準差為σ0(已知)的正態分布,其概率密度函數為
可靠度函數為
式中: μ 為對數壽命均值;Φ(·)為標準正態分布函數。
現進行了一組n 個該產品的定數截尾試驗, 前r 個為失效數據xi=lgNi,i=1,2,…,r,后n-r 個為未失效數據,且xi=xr=lgNr,i=r+1,r+2,…,n。則可以證明,該產品置信度為γ、可靠度為R 的對數可靠壽命xR單側置信下限xRL,γ可由下式給出
其置信度為γ、可靠度為R 的可靠壽命NR單側置信下限NRL,γ則為
式中:M 根據數值計算精度要求進行取值(如104,105,106等),并且應使Mγ 為整數。然后,調整式(8)中的γ 至某一值γ**,使得式(5)中γ*等于γ,此時γ**即為所求值。
對于工程上需要計算置信度為γ、 可靠度為R 的可靠壽命NR單側置信上限NRU,γ的情況,則將上面公式中的γ 用1-γ 代替即可。
現證明如下: 首先, 根據前r 個失效數據xi,i=1,2,…,r, 可以按照完全數據處理方法求得該產品置信度為γ、可靠度為R 的對數可靠壽命xR單側置信下限為
滿足
然后, 利用其余n-r 個未失效數據xi=lgNr,i=r+1,r+2,…,n,對的置信度進行Bayes 更新。 即將前r 個失效數據求得的式(10)作為先驗分布,并將后n-r 個未失效數據作為樣本數據,通過Bayes 公式求得后驗分布。 由于先驗分布直接根據試驗數據求得, 所以確保了后驗分布的客觀真實。 更新后的置信度γ*可以表示為
式中:g(xR)為xR的置信分布[5]。
因此,可將式(12)和式(13)變換為
而式(16)和式(17)可以通過下面兩式進行數值計算:
代入式(11),可以得到
式中:
最后,調整式(23)中的置信度γ 至γ**,使得式(20)中的γ*=γ,此時即可求得該產品置信度為γ、可靠度為R 的對數可靠壽命單側置信下限為
將上述證明過程中的置信度換成置信水平, 仍然成立。 證畢!
1.2 定數截尾數據可靠度評估方法
由置信限曲線的等同性可知, 該產品在給定時間x=lgN 處置信度為γ 的可靠度單側置信下限RL,γ為
2 正態分布定時截尾試驗可靠性評估
同樣, 定時截尾試驗也是工程上一類常見的重要試驗,它要求試驗達到事先規定的試驗時間停止試驗。下面給出產品對數壽命遵循正態分布情況下的定時截尾數據可靠性評估方法。
2.1 定時截尾數據可靠壽命評估方法
設某產品對數壽命X=lgN 遵循標準差為σ0(已知)的正態分布,如式(1)所示。 現進行了一組n 個該產品的定時截尾試驗,前r 個為失效數據xi=lgNi,i=1,2,…,r,后n-r個為未失效數據,且xi=x0=lgN0,i=r+1,r+2,…,n,其中N0為試驗截尾時間。 針對定時截尾試驗情況,可將一個未失效數據xr+1=x0看作失效數據,進而將其轉化為定數截尾試驗情況進行處理, 得到的結果將偏于保守。 即在式(3)中用r+1 代替r,就可以根據定時截尾試驗數據求得置信水平為γ、可靠度為R 的對數可靠壽命xR單側置信下限為
其置信水平為γ、 可靠度為R 的可靠壽命NR單側置信下限NRL,γ仍由式(4)計算。
對于工程上要計算置信水平為γ, 可靠度為R 的可靠壽命NR單側置信上限NRU,γ的情況,只需將式(6)中的xr換成x0,式(8)中的γ 換成1-γ 即可。
特別地,當定時截尾壽命數據均為未失效數據時,該產品置信水平為γ、 可靠度為R 的對數可靠壽命單側置信下限為
2.2 定時截尾數據可靠度評估方法
由置信限曲線的等同性可知,該產品在給定時間x=lgN處置信水平為γ 的可靠度單側置信下限RL,γ由下式給出
3 仿真驗證
本文方法除了嚴格的理論推導外, 還進行了大量的Monte Carlo 模擬仿真驗證,其結果表明:正態分布定數截尾數據可靠性評估方法嚴格滿足置信度要求; 而正態分布定時截尾數據可靠性評估方法則通常高于置信度,偏于安全,滿足置信水平要求。下面給出仿真方法和幾組仿真結果。
仿真驗證方法: 設某產品的對數壽命遵循正態分布N(μ,σ02),首先通過Monte Carlo 方法從其對數壽命母體中進行隨機抽樣, 分別產生該產品定數或定時截尾壽命數據。 然后根據本文方法求得其置信水平為γ、可靠度為R 的對數可靠壽命單側置信下限xRL,γ,并使之與對數可靠壽命真值xR=μ-uRσ0進行比較。重復仿真m 次,統計xRL,γ小于等于xR的頻率作為仿真置信度γ′,比較仿真置信度γ′與設定的置信度γ,即可驗證本文方法的正確性。
定數截尾仿真驗證:在每次仿真試驗中,產生一組定數截尾壽命數據,重復仿真次數m=50000 次,表1 列出了不同條件下可靠度R=0.999 的定數截尾仿真驗證結果。可以看到,仿真置信度γ′均非常接近于設定的置信度γ。倘若增加重復仿真次數m, 則仿真置信度γ′將與設定的置信度γ 完全相等。 表明本文提出的正態分布定數截尾數據可靠壽命單側置信下限評估方法滿足置信度要求。
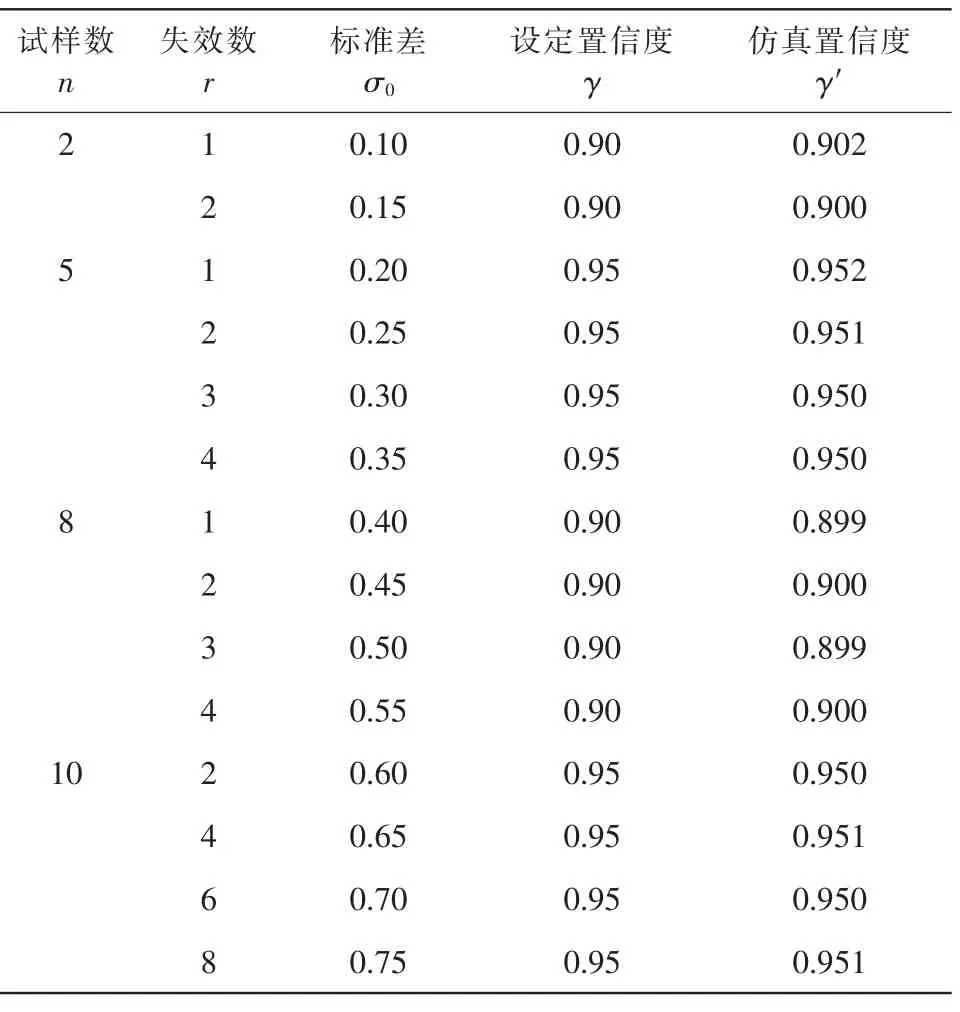
表1 定數截尾仿真驗證結果
定時截尾仿真驗證:在每次仿真試驗中,產生一組定時截尾壽命數據,重復仿真次數m=50000 次,表2 列出了不同條件下可靠度R=0.999 的定時截尾仿真驗證結果。 可以看到,仿真置信度γ′均高于設定置信度γ,表明本文提出的正態分布定時截尾數據可靠壽命單側置信下限評估方法滿足置信水平要求,略偏于保守。 此外,可以發現隨著截尾時間的增加, 仿真置信度越加接近于設定置信度。倘若無限延長截尾時間,該方法將會退化為完全數據處理方法。

表2 定時截尾仿真驗證結果
4 算例
已知某型航空發動機渦輪葉片對數壽命遵循標準差為σ0=0.15 的正態分布。現從一批該產品中隨機抽取5 個進行振動疲勞試驗, 規定循環次數達到2×107時停止試驗,試驗數據如表3 所示。下面采用本文方法對該產品的可靠性進行評估。

表3 某型航空發動機渦輪葉片定時截尾試驗數據
首先,根據本文2.1 節方法,將一個未失效數據N2視為失效。 由式(9),利用失效數據Ni(i=1,2)計算該產品置信水平γ=0.95、 可靠度R=0.9987 的可靠壽命單側置信下限為
最后,調整式(23)中的置信水平γ=0.95 至γ**=0.36,使得γ*=γ。 根據式(26)和式(4)可計算該產品置信水平γ=0.95,可靠度R=0.9987 的可靠壽命單側置信下限NRL,γ為
5 結論
提出一種正態分布定數截尾數據可靠性評估方法,能夠根據定數截尾壽命試驗數據評估產品高置信度、高可靠度的可靠壽命單側置信限, 以及給定時刻下高置信度的可靠度單側置信下限, 解決了長期以來正態分布定數截尾數據難以進行可靠性評估的問題。
針對工程上常見的正態分布定時截尾壽命試驗,進一步建立一種正態分布定時截尾數據可靠性評估方法,使工程上許多原先無法處理的定時截尾壽命試驗數據得以統計分析,實現小樣本可靠性評估。
嚴格的理論推導和大量的Monte Carlo 模擬仿真,證明了本文方法的正確性。

