融入新時代中國精神的高職應用專業教改實踐

蘇丹

摘?要：為了適應時代的發展需要，以及中國特色社會主義建設的戰略需要，高職應用數學教學與新時代中國精神相融合刻不容緩。根據高職應用數學課程中的實際情況，從教學內容、學情分析、教學目標、教學過程和教學評價等方面，探討了在數學課程中融入“中國精神”的課程思政教學設計的結構框架，并給出導數與兩個“中國速度”案例教學課程思政的可行性。

關鍵詞：中國精神；?數學育人；導數與中國速度

中圖分類號：F27?????文獻標識碼：A??????doi：10.19311/j.cnki.16723198.2023.24.030

人無精神則不立，國無精神則不強。“中國精神”就是以愛國主義為核心的民族精神，以改革創新為核心的時代精神。如果能把“中國精神”融入高數的教學中，不僅有利于讓學生培養愛國情懷、民族自豪感，而且能提高學生學習高數的興趣。因此，通過講述導數與“中國速度”的實際案例，在課程教學中滲透思政教育，使思政教育與專業知識傳授有機融合，挖掘高等數學中相關思政元素對于培養學生正確的世界觀、人生觀和價值觀具有重要意義，從而讓學生更有信心應用數學解決其他專業的實際問題，更有利于發揮課堂思政的育人功能。

百年大計，教育為本。課程思政不僅是一種教學理念，更是一種教育方法。課程思政教學是將思想政治元素融入到各門課程中去，使各類課程與思想政治課共同發揮育人作用，最終實現立德樹人的目的。以邏輯推理為主的“硬核”的數學課程，就很難和思政教學渾然一體。所以，我們在教學實踐中要潛移默化地將“中國精神”滲透到高等數學的教育實踐之中，充分運用鮮活的資料，開展教學思政探索。近年來，已有大量文獻表明高職應用數學基礎課程思政的實踐和探索正在進行，如：陳亮探討了將高職數學與中國傳統文化進行融合，實現學生的素質教育和綜合能力；趙永輝論述了通過應用數學典型情境中的數學之美使學生認識到數學的實用價值；王慧等提出在數學分析課程中融入課程思政的途徑。本文將從以下幾個方面探討高職應用數學課程思政的結構框架。

1?教學內容

微積分內容是理工類專業學生進行專業學習的重要工具和基礎。而導數概念是微積分的重要部分，其概念雖然比較難理解，卻非常有用，是學習其他各類學科的重要輔助工具，對學生后期發展有極大的作用。

該課程設計目的是通過深入剖析學校思政教育活動的具體實踐，并結合導數定義在思想教育活動中3個恰當的時間節點上，不著痕跡地滲透“中國精神”。首先，感受和認識“中國速度”。其次，用發展的唯物主義觀點“看”數學。最后，學會學以致用來完成“互動接收”。

2?學情分析

學習本課程前需掌握函數的概念、極限的概念與思想，以及在初高中就學過的計算平均速度、圓的切線等知識，從而為本節課的學習奠定基礎。由于導數的概念比較抽象，直接給出導數定義是不可行的。因此，在教學前，先讓學生自行查找和上傳“中國速度”的相關視頻，調動學生的學習興趣。并將學生熟悉的短跑飛人蘇炳添和中國復興號的視頻背后的實際數學問題—瞬時速度和曲線切線，作為“中國精神”融入數學案例教學過程的典型代表。引導學生對以上的兩個“中國速度”的案例進行觀察、歸納，總結出它們的共同特性，最后教師抽象概括出導數的概念，讓學生體會“中國速度”背后的“中國精神”，使學生充分樹立對“改革創新是新時代的迫切要求”的科學認識，增強責任感、夯實創新基礎，大膽投身改革創新實踐。

3?教學目標

從認識上，通過對兩個“中國速度”的案例剖析，可以經歷從平均變化率轉換到瞬時變化率的過程，從而掌握了導數定義的實際背景，并明白了瞬時變化率就是導數。在能力上，學會使用逼近方法、類比方法；學會解決其他專業的實際問題，例如化工專業中的瞬時反應速率、用料最節省等實際應用問題。在素質上，培養學生敢于突破自我的拼搏精神；培養學生的愛國情懷、民族自豪感。在教學過程中，選出兩個有代表性的“中國速度”的視頻，進行案例教學，引導學生觀察、思考，并嘗試進行歸納總結兩個案例中的共同特征，從而引導學生攻克導數概念的重、難點。

4?教學過程

4.1?課前云端預知

在課堂教學前，教師可在職教云平臺發起實驗任務，以“中國速度”為關鍵詞，搜索相關視頻并上傳到智慧職教平臺。引導學生搜集相關資料，并思考以下的兩個問題。

（1）運動員蘇炳添在百米比賽時，某時刻的瞬時速度如何求？

（2）當中國名片復興號在行駛轉彎時，要使中國高鐵復興號安全穩定地運行，轉彎設計會涉及到切線斜率問題，切線的斜率怎么解決？

通過創設問題情景，提升學生對中國科技發展的關注，增強學生的民族自豪感和愛國情懷。

4.2?課中案例驅動

線下課程在多媒體教室進行，從大家上傳到職教云平臺有關“中國速度”的視頻中，選出2個具有代表性的案例：“奧運英雄”—蘇炳添和“中國名片”—復興號，進行下面的案例教學。

案例1“奧運英雄”——蘇炳添

2020年東京奧運會的男子個人百米淘汰賽上，運動員蘇炳添以9秒83的速度突破亞洲紀錄，成為第一個進入奧運會男子“飛人”決賽的中國人。也是電子計時時代第一位闖入奧運百米決賽的亞洲選手！通過觀看奧運英雄蘇炳添百米比賽視頻，讓學生體會努力拼搏，不給自己的人生設限，努力挖掘自身潛力，敢于突破自我的拼搏精神。案例教學中融入“中國速度”，同時也增強學生的愛國情懷和民族自豪感。

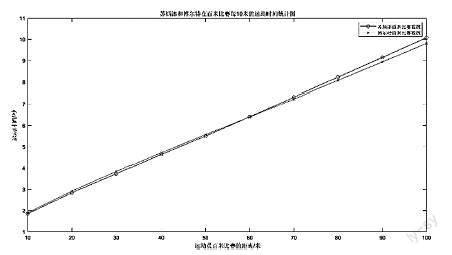
如何求解奧運英雄蘇炳添在百米比賽時，某時刻的瞬時速度？我們可以根據2016年里約奧運會，我國運動員蘇炳添和牙買加運動員博爾特百米比賽的數據，進行分析。通過從國際田徑業余聯合會（IAAF）官方網站上獲取的這兩名選手參賽視頻，利用Dartfish軟件，為他們的前10秒做了報秒計算，并通過Matlab等軟件制繪出了他們的折線對比圖（見下圖）。

由此，可以看出，運動員蘇炳添在前1/3段路程中，比運動員博爾特運動得快；博爾特在后2/3段路程中，比蘇炳添運動得快。我們通常用平均速度來比較運動員運動的快慢。這就給出一個求解思路，若要求解變速直線運動的瞬時速度問題，可以引導學生通過平均速度來求解，也就是用已知的知識來探究未知的知識。求蘇炳添在某時刻的瞬時速度，把運動員蘇炳添看作是一個質點，設質點做變速直線運動，其位移函數為s=st，如何求得t0時刻的瞬時速度？

為了求t0時刻的瞬時速度，可在t0附近取一點t，將t0到t這段時間間隔記作Δt。因此，這段時間間隔內的平均速度就可以得出。平均速度等于這段時間所經過的路程除以這段時間間隔，即v=st－s（t0）t－t0。當時間間隔變得非常非常小的時候，也就是Δt→0時，t無限接近t0，那么平均速度v-就無限接近t0時刻的瞬時速度。根據極限的思想：逼近的思想，我們可引入極限的概念，用平均速度近似的表示瞬時速度。若平均速度的極限存在，那么該極限就是t0時刻的瞬時速度。

案例2?“中國名片”——復興號

新一代標準高速動車組“復興號”是中國自主研發、具有完全知識產權的新一代高速列車，它集成了大量現代高新技術，牽引、制動、網絡、轉向架、輪軸等關鍵技術實現重要突破，是中國科技創新又一重大成果。至2016年7月，中國標準動車組已在世界上率先進行時速420千米的交會與重聯運行測試；2017年6月25日，中國標準動車組被官方正式命名為“復興號”。?2017年9月21日，中國高速鐵路實施了最新的列車運行圖，國內“復興號”動車組在京滬高鐵率先恢復350公里航速運行，我國再次變成當今世界上動車商業運營效率最快的國家。通過觀看學生自行查找的復興號的視頻，體會“中國速度”之快。我國創新能力的標志性成果之一——高鐵，黨的十八大以來，習近平總書記在出訪時，曾多次向世界展示過這張“中國名片”。

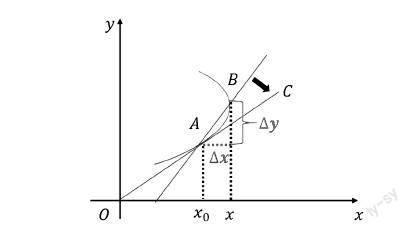
當高鐵駛入彎道時，為保持其平穩運行，彎道設計會涉及到曲線在某點的斜率，那么如何求解曲線的切線斜率？

為了求曲線的切線斜率，可以從已經學過的知識去探究，可以通過割線的斜率來求解切線斜率。在A點附近取一點B，B也是曲線一點，鏈接AB得到一條割線。割線的斜率就可以表示為kAB=tanα=ΔyΔx=y－y0x－x0，（其中，α是割線與x軸正方向的夾角）。當B點沿著曲線向A點無線靠近，Δx→0時，割線AB斜率就可以近似地表示切線AD斜率。同樣的，根據極限的思想，在這里也引入極限的概念，用割線AB斜率近似地表示切線斜率。

通過對以上的兩個“中國速度”的引例的探究，可催化引導學生進行觀察、分析、歸納和總結它們之間的相同點，提升學生思辨能力。可以看出，雖然的它們的實際意義不同，但最終得到的表達式的結構是相同的。無論是求奧運英雄蘇炳添在某時刻的瞬時速度，還是求中國名片復興號在駛入彎道時，某點的切線斜率，最后得到表達式的結構都是：平均變化率的極限。由此可引入導數的概念，即定義。

定義設函數y=f（x）在點x0處及其附近有定義，如果極限

limx→x0ΔyΔx=limΔx→0fx0+Δx－f（x0）Δx=limx→x0fx－f（x0）x－x0，

存在，則稱函數f（x）在點x0處可導，并稱此極限值為函數f（x）在點x0處的導數，記為f′（x0），即

f′x0=limx→x0ΔyΔx=limΔx→0fx0+Δx－f（x0）Δx=limx→x0fx－f（x0）x－x0

函數值與自變量兩者改變量的比值ΔyΔx可稱為平均變化率，而導數f′（x0）表示函數f（x）在x0處對自變量x的變化率，所以導數反映了函數值隨自變量變化而變化的快慢程度，換句話說，導數的實質就是平均變化率的極限。

在案例1中，t0時刻的瞬時速度可表示為s′（t0），其物理意義為運動員蘇炳添在t0時刻的瞬時速度。在案例2中，在點A（x0，f（x0））處的切線斜率可表示為f′（x0），其幾何意義為高鐵行駛彎道時在（x0，f（x0））的切線斜率。

那么函數在某一點是否可導？可通過上式平均變化率的極限進行判斷。若上述極限存在，則函數f（x）在點x0處可導；如果上述極限不存在，則稱函數f（x）在點x0處不可導。因此導數的定義式不僅用于判定是否可導，還可以用于相關計算。

4.3?課后實踐研學

以知促行，激發學生創造力。課后讓學生嘗試利用導數的定義求解各專業的實際應用問題，導數知識學以致用，從而完成“互動接收”。

例?一級化學反應A+B→C。在某溫度時，在2L的密封容器中，A和B的初始濃度相同：A=B=amol/L.則C=a2ktakt+2其中k為常數。

（1）求在時刻t的反應速度？

（2）當t→+

濃度會發生什么變化？

（3）?當t→+

反應速率會發生什么變化？

設置小組課后答題任務，讓學生嘗試給出問題（1）的解題過程，并引導學生探究問題（2）（3）在實際情況中的實用意義。

5?教學評價

構建以學生為主的形成性和多樣化的評價系統，有助于探討與數學有關學科的思政模式。以線上練習、教學互動、期末考試、案例應用為切入點，同時還根據學生的整體學習態度、考試認真程度等的綜合分析結果，對平行班級采取圖表1中所示的評分系統進行了過程性比較研究，從而為告知學生應用數學的課堂思政的系統性提供了有力保障。

6?結語

立德樹人是教育的根本任務。新時期新征程，“中國精神”為講好思政課提出了豐富多彩、鮮活的事例和材料，我們善用思政材料，深度挖掘課程思政教育功能的具體案例，在教學過程中3個恰當的節點處，將導數定義自然地引入新時代中國精神，通過“理實一體”模式充實對學生的認識，激發學生對思維濃厚興趣，對學生的思維行為加以引導與教育，實現為國家、為人民、為社會培育德藝雙馨應用型人才的教育目的。

參考文獻

［1］習近平.在第十九屆中央政治局第三十九次集體學習時的講話[N].中國新聞網，20220527.

[2]張大良.課程思政：新時期立德樹人的根本遵循[J].中國高教研究，2021，1（1）：59.

[3]陳超.高職數學教學中滲透中國傳統文化的研究[J].當代教育實踐與教學研究，2022，5051.

[4]趙永輝，滑會超.高職數學課程思政建設路徑探索[J].成才之路，2023，5（14）：2124.

[5]王慧，黃敏，張洪濤;等.數學分析“課程思政”的實踐與思考[J].創新教育研究，2019，7（5）：675678.

[6]劉薇，常振海，高忠社，等.融入課程思政元素的導數定義教學設計[J].通化師范學院學報，2021，10（42）：2934.

[7]同濟大學數學系.高等數學（第七版）[M].北京：高等教育出版社，2014.