基于貪婪最佳優先搜索算法的方形件排樣優化問題研究
劉艷麗,李軍祥 (上海理工大學管理學院,上海 200093)
0 引 言
受益于我國良好的制造業基礎及政府對制造業智能化轉型升級的大力推動,近年來智能制造行業的發展較為迅速。智能制造裝備具有分析、推理和感知等功能,它是智能技術、信息技術和先進制造技術的集成和深度融合[1]。隨著生產技術的發展,在工業4.0 的數字化轉型背景下,眾多企業開始以個性化定制和供應鏈整合為切入,實現以用戶為中心的大規模個性化定制[2]。當前在新一代數字科技的支撐和引領下,越來越多新興的智能制造企業開始進行數字化升級、轉型和再造,建設數字化智能工廠,提升智能制造能力和個性化定制能力,使得在面對用戶需求時能夠做到快速響應、有效應變。
方形件產品是指采用板材為主要用料,經過一系列程序加工后生成板式配件,再按照圖紙進行組裝后形成的一類產品[3]。這類產品多用于制造企業,主要面向包括通訊設備、精密機床制造、消費性電子、金屬板材等產業的多個領域。為了保量和以最小化的成本制造滿足顧客需求的個性化產品,智能制造企業大多采用多品種、小批量和個性化定制方式進行生產,采用“訂單組批+批量生產+訂單分揀”的模式,通過訂單組批來實現批量切割以更好地發揮規模效益,再整合訂單中的共同需求得到不同客戶的揀取信息進行訂單分揀[4]。
其中,個性化定制生產模式涉及排樣優化這一關鍵性問題。排樣優化本質上是一個下料問題,是指將一系列方形件按最優方式在板材上進行排布,要求方形件排放在板材內,各個方形件互不重疊,并滿足一定的工藝要求。優化的目標是生成最合理的排樣方式,最大限度地節約材料、提高材料利用率,實現切割過程的簡化。該問題是一個組合優化問題,計算復雜度很高,也是運籌學領域一個非常重要的分支。許多制造企業生產產品和零部件的第一步即下料,過程中會消耗大量的材料和資源,如果不合理規劃則會造成巨大的浪費。因此,本文構建了一個排樣優化模型,考慮了一系列相關約束,利用貪婪最佳優先搜索算法對模型進行求解,針對各數據集給出其最佳的排樣效果圖,驗證了模型的有效性及可行性。
1 問題描述及假設
1.1 排樣優化問題描述
本文采用3 階段切割方式,要求只能進行齊頭切且每個階段只能選擇一個方向進行切割。齊頭切也稱“一刀切”,要求每次進行直線切割時板材都能分成兩塊[5]。3 階段切割方式如圖1 所示,第1 階段進行橫向切割,此時生成的模塊稱為Stripe(條帶),如Stripe1 和Stripe2;第2 階段進行縱向切割生成的模塊稱為Stack(棧),如Stripe1 被切割分成Stack1、Stack2 和Stack3;接下來進行第三階段的橫向切割,生成的模塊稱之為Item(產品項),如Stack1 繼續被分成Item1、Item2 和Item3。本文基于以上規則對方形件進行切割。排樣優化問題屬于二維組合優化問題,通過研究方形件在板材上的排放順序和排放方式,使得方形件在板材上組合排放的利用率達到最高。具體來說就是根據同一個生產排次內的方形件尺寸和數量進行原片規格和數量的選擇。該問題要求在滿足生產訂單需求和相關約束條件下,進行下料排樣優化,盡可能減少板材用量,避免浪費,使板材原片的利用率達到最大。其中需要考慮的約束條件如下:(1) 在相同棧里的產品項的寬度(或長度) 應該相同;(2) 最終切割生成的產品項是完整的,非拼接而成。該問題本質上是一個二維裝箱問題,也就是將若干個矩形物品裝進矩形的箱子中,并且在裝箱的過程中不允許將矩形物品斜著放,必須平行于橫坐標。一般來說求解的目標是使箱子的數目或者是空間占用率最小。當用于矩陣存儲時,求解的最優目標便是箱子的空間占用率最大化。
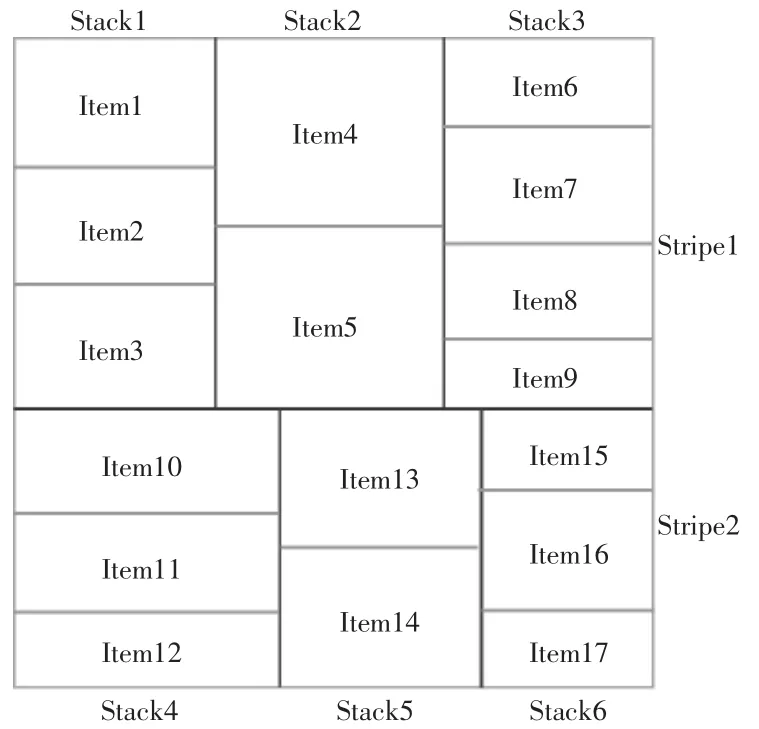
圖1 不同切割階段的形式定義
1.2 假設與約束條件
(1) 只考慮齊頭切的直線切割方式,切割方向均垂直于板材的一條邊,且每次切割板材都可以分成兩塊;
(2) 切割階段數不超過3,且同一個階段的切割方向相同;
(3) 排樣方式為精確排樣,即在三個階段內能切割出準確尺寸的方形件;
(4) 板材原片只有一種規格并且數量充足;
(5) 排樣方案不考慮切割縫隙寬度的影響。
2 排樣優化模型構建
方形件排樣優化問題用數學語言可以描述為:將n個不同規格的方形零件{k1,k2,…,kn}排入到一個寬度為M,長度L的板材原片中,且板材原片數充足,待排樣的毛坯有m種,長、寬、高需求量分別為(li,wi,di),其中i為毛坯型號。B={1,2,…,b}是一個由b個相同的方形件組成的集合,stack(k∈B)的寬度為W,高度為H。N={1,2,…,n}是一個由n個item組成的集合,其中n≥b。
設板材原片左下角為原點(0,0),左上角為(0,M),右下角為(L,0),x和y表示item在其分配的stack內的位置,即方形件ki的左上角坐標為(xi,yi),其中xi≥0,yi≥0,i∈N*。第i個item(i∈N)的寬度wi≤W,高度hi≤H,若ki旋轉了90°,則其寬度和高度互換,ri為是否旋轉變量,ri=1 表示旋轉,ri=0 不旋轉,則ki右下角坐標為(xi+(1-ri)wi+rihi,yi-(1-ri)hi-riwi)。N*表示由旋轉的重復項附加的集合N,第i個item(i∈N)的重復項是寬度為hi,高度為wi的第n+i項。當第i個由旋轉后的重復項item不能進入stack,即wi≤H,hi≤H,則其相應的決策變量沒有被定義,因此忽略不計,其余相應的變量均如此。因此利用(xi,yi)、wi、hi及ri即可確定ki在板材原片中的排樣位置,因此方形件ki可用一個五元組表示[6]:
f表示將item分配到stack,如果第i個item被分配到第k個stack中,其中fik=1,則i∈N*,k∈B,否則為0。l和u是二進制的,它們表示兩個item的相對位置lij=1(uij=1 ),i∈N*,j∈N*,i≠j,j≠i+n且i≠j+n,用于當i和j在同一個stack中使i位于j的左邊。P={p1,…,pk}明確每種排樣方式中所包含的i型毛坯數量aij、排列位置和順序,確定排樣方式的使用頻率mj,i=1,2,…,m,j=1,2,…,m,其中mj是整型決策變量。
在滿足訂單需求和相關約束條件下,使得板材原片的用量盡可能少,即使板材原片利用率(零件占用面積/板材原片面積)最大,從而達到節省材料的目的。要求滿足的約束條件如下:
(1)ki與kj互不重疊:
其中:(i,j)∈N*2,i≠j,j≠i+n,i≠j+n。
(2) 在板材原片的長度方向,所有零件長度之和應不大于板材原片長度L,即:
(3) 在板材原片的寬度方向,所有零件長度之和應不大于板材原片的寬度M,即:
(4) 每個item(i∈N)必須在沒有重疊的情況下進行包裝,并且ki必須完全包含在其分配的stack中:
(5)ki的邊必須與板材原片的邊平行,且在放入時可以進行90°旋轉:
(6) 最終切割生成的產品項是完整的,非拼接而成:
其中:xj∈N,j=1,2,…,K。
這是一個二維三階段剪切下料問題,求解的目標可以簡述為使用數量最少的板材原片,排完全部數據集給出的所有訂單毛坯[7]。通過建立混合整數規劃模型確定所求的目標函數如下:
其中:z為板材原片的數量,i為毛坯型號,m為待排樣的毛坯種類,aij為毛坯數量,K為排樣方式的種類,xj為排樣方式使用的頻率且為整型決策變量。
在本文中排樣優化問題的解由三階段同質排樣方式(3H) 組成,滿足了題中切割時在相同棧里的產品項的寬度或長度相同約束,而3H中存在約束三階段排樣問題,即求解毛坯在原片板材上的3H排樣方式所得的毛坯價值最大化,相關約束排樣問題的整數規劃模型表示如下:
其中:Zp表示3H排樣方式最大化板材中所包含的毛坯總價值,ai表示3H中的i型毛坯的數量,vi表示i型毛坯的價值,ri表示i型毛坯的當前剩余需求量。
3 仿真實驗設計與分析
3.1 仿真實驗
實驗環境:硬件配置為Intel 酷睿i5,主頻1.80GHz,內存12GB;軟件配置為Windows11 64 位操作系統;求解均使用MatlabR2018b 編程實現。在程序測試時,設定板材原片尺寸為2 440×1 220,切縫寬度為1,輸入參數為:(1) 單個批次產品項總數上限max_item_num=1 000;(2) 單個批次產品項的面積總和上限max_item_area=250(m2)。為了增加實驗的可信度,本文針對排樣優化問題共收集了4 個數據集進行算法的驗證,分別為數據集dataA1、dataA2、dataA3 和dataA4。各數據集均源于中國研究生創新實踐系列大賽網站(https://cpipc.acge.org.cn),其中各個數據集是相互獨立的。
3.2 模型求解與結果分析
本文運用貪婪最佳優先搜索算法對混合整數規劃模型進行求解。貪婪最佳優先搜索是一種啟發式搜索算法,也可以把它看成廣度優先搜索算法的一種改進;算法思想是將節點按距離目標的距離進行排序,然后以這個距離為代價選擇待擴展的節點[8]。在對方形件排樣優化過程中,每一步都選用當下解空間的最優排放順序,通過一次遍歷就可以得到最優解。以下是程序運行出來的排樣方案效果圖,因數量太多,此處針對每個數據集僅列舉部分圖片。圖2 至圖5 分別為數據集dataA1、dataA2、dataA3和dataA4 的部分排樣圖。從圖中可知,每一塊板材都得到了極大地利用,浪費空間很小。

圖2 dataA1 排樣圖
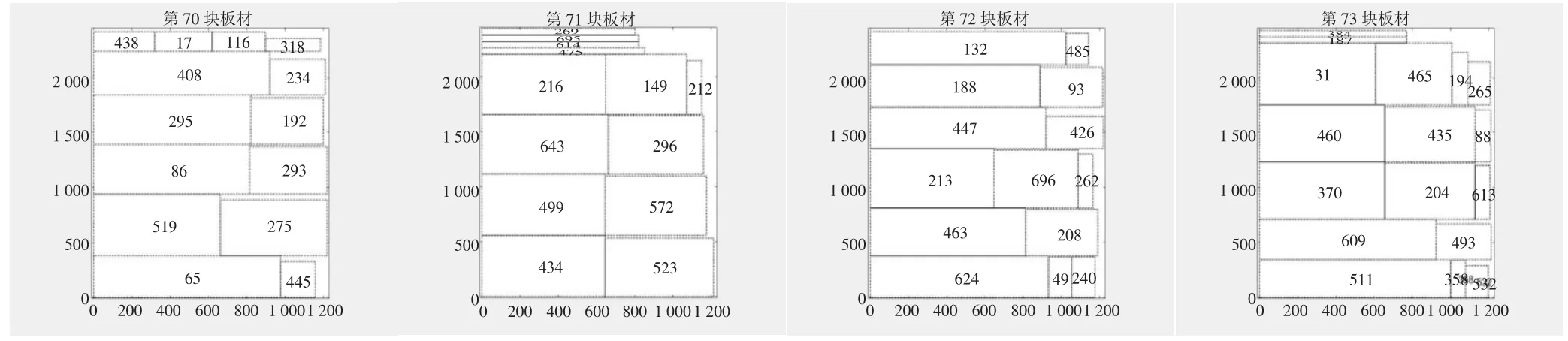
圖3 dataA2 排樣圖
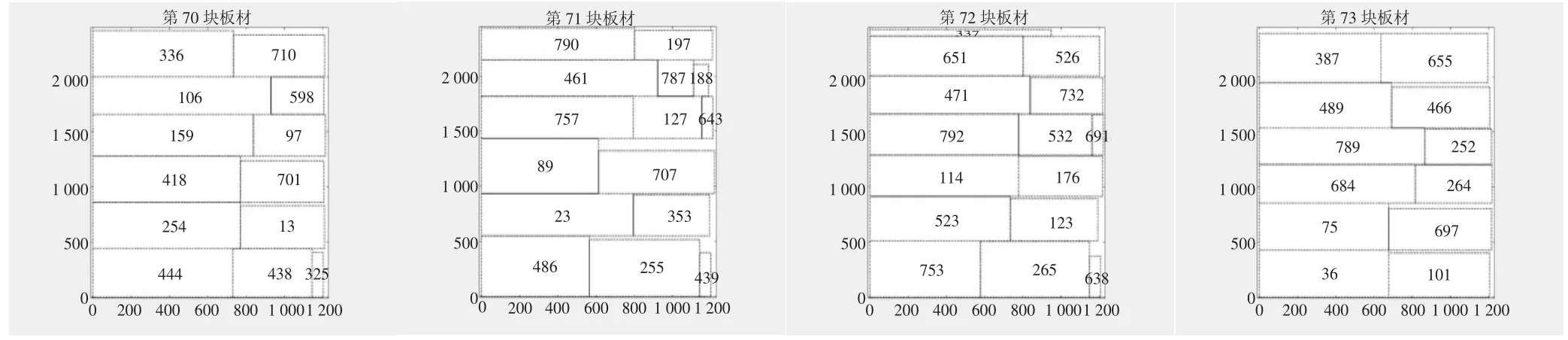
圖4 dataA3 排樣圖

圖5 dataA4 排樣圖
本文以板材利用率(產品項面積之和/使用原片面積之和) 作為結果指標,實驗結果對比如表1 所示,板材利用率分別為91.70%、90.97%、93.97%和95.07%,說明該算法在節省板材資源和提高板材利用率方面效果顯著。本文算法在dadaA1、dataA2、dataA3 和dataA4 數據集生成排樣方案的過程中分別考察了90 個、90 個、88 個和85 個排樣方式,平均每個排樣方式耗時0.05s。由此可見該算法還具有靈活、高效和計算方便的優點。

表1 實驗結果對比表
4 小 結
排樣優化問題廣泛地存在于產品制造企業,如3C、板式家具、玻璃、鈑金件等行業的生產過程中,一個好的優化算法可解決材料利用率低、生產效率低及個性化與生產高效性之間的矛盾。針對排樣優化問題,本文設計了一種基于貪婪最佳優先搜索算法生成相同棧里的產品項的寬度或長度相同的三段排樣方式,減少了原材料的浪費,提高了板材利用率,為制造企業進行大規模個性化定制提供了可能。本文模型結合實際情況建立,與實際情況密切聯系,通用性和推廣性很強。同時實驗結果表明,本文的算法可以有效地減少板材用量,且計算時間可以滿足實際應用需要,具有一定的現實意義。此外訂單組批問題是個性化生產模式中的另一關鍵問題,下一步將對此問題進行深入研究,通過訂單組批來保證貨物的交貨期,幫助企業實現訂單的批量化生產。

