不同陣列布局的空間譜測向方法的抗多徑性能研究
崔 宏,馬 杰
(青島市無線電監測站,山東 青島 266075)
0 引言
在城市復雜環境中,無線電波的傳輸具有時、頻、空域的復雜性,反射、繞射等現象會引起顯著的多徑傳播效應,導致在監測接收端會收到從不同方向入射的同一信號的多徑分量,此時會對測向系統造成嚴重的影響,產生偏差較大乃至錯誤的結果[1]。空間譜測向系統具有一定的同頻信號和信號的多徑分量分離能力,是應對該問題的一類有效方法[1],在多個領域得到了成功的應用,成為近 二十年無線電測向技術的研究熱點[2]。Belloni等[3]給出了空間譜估計的理論框架。文獻[4]給出了典型空間譜細子算法的性能比較,并對其工程實現的相關考慮進行了研究[5-6]。文獻[7-9]給出了在復雜無線電監測場景下應用空間譜測向算法的思考,指出了當前的局限性和發展趨勢。
針對同頻多信源和多徑2類復雜場景,文 獻[10]和文獻[11-12]分別研究了空間譜算法的適用性,文獻[13]進一步研究了存在強干擾和多徑這一復雜電磁環境下,對應的改進MUSIC測向算法。同時,在如何優化MUSIC陣列,提高其性能和估計能力方面,也有文獻做出了深入的探索。其中文 獻[14]提出了基于矩陣重構技術的新型MUSIC算法,使其具備波達方向和擴展角同時估計的能力;文獻[15]提出了一種新型的互質陣列,在同樣陣元數下,能夠實現更大的陣列孔徑、更高的測向精度、更高的自由度以及更高的分辨率;文獻[16]針對非均勻圓陣這一較為特殊的陣列,研究了相應測向算法的性能;文獻[17]則另辟蹊徑,提出了利用粒子濾波進行測向算法的抗多徑,取得了一定的效果。
根據上述分析,有必要進一步考慮任意陣列流型這一最具普適性的陣列結構,深入研究存在多徑,特別是時延較小的強相干多徑模式下,MUSIC算法的抗多徑性能。可通過理論與仿真相結合的方式,針對典型測向陣列流型,對不同時延、不同徑數下的性能進行深入評估,從而為實際場景下有效區分多徑信號提供必要的理論依據。
本文第一節首先對現有傳統陣列結構進行拓展,首次給出了任意陣列這一更具一般性的陣列布局下,對應的空間譜測向算法。第二節重點針對圓型陣列布局,通過仿真來深入地定量評估不同多徑時延和徑數下的測向性能,特別是對時延小于一個符號周期的多徑分量強相干的情況,率先進行了深入研究;同時也進一步探索了隨機陣列對于多徑信號區分的可行性。最后進行了小結。
1 多徑傳播環境下任意陣列流型的信號測向算法設計
1.1 多徑模式下陣列模型
考慮三維空間模型,假設陣元有M個,考慮把第一個陣列對應的位置作為坐標零點,可以記為q1=[0,0,0]T,依次可以把其他的陣元位置標記為qj=[xj,yj,zj](j=2,3,…,M)。另外,考慮入射的徑數為P(P≥1),第i個點相對坐標零點的方位角和俯仰角向量記為[φi,θi] (i=1,2,…,N)。考慮水平方向構成XOY平面,高度為Z平面,定義俯仰角φi為入射電波與XOY平面的夾角,方位角θi為入射電波與Y軸的夾角。基于此模型,對應的三維方位矢量可以表示為ui=[cosφisinθi,cosφicosθi, sinφi]。此時若考慮第j個陣元接收到的信號,則xj(t)可以表示為[18]:
(1)
式中:fi為第i個信源的中心頻率,si(t)為第i個入射信源,nj(t)為第j個接收陣元的噪聲,一般為加性高斯白噪聲;τij為第i個信源和第j個接收陣元相對于坐標零點的時延。
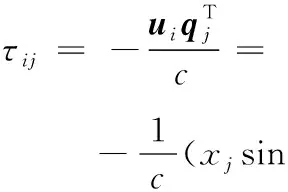
(2)
式中:c為光速。根據上述分析,可以定義第i個信源的陣列流型向量a(θi,φi)和陣列流型矩陣A分別為:
(3)
(4)
根據上述模型,信號向量和噪聲向量可以分別表示為S(t)和N(t),故可以定義接收信號向量X(t)為:
(5)
(6)
(7)
因此,在多徑環境下,空間多陣元的陣列模型可以寫為:
X(t)=AS(t)+N(t)。
(8)
上述模型即為在多徑傳播環境下,多陣元的接收陣列模型,可以通過該式設計相應的波達方向估計算法。
1.2 基于MUSIC算法的多陣元多徑信號來波方向估計
本節基于式(8)的模型,推導對應的MUSIC[4]算法,給出多徑傳播條件下多陣元模型的估計步驟:
步驟①:假設連續進行了P次采樣,每一時刻各個陣元得到的接收信號向量為X(t) ,那么可以估計得到其協方差矩陣R如下:
(9)
步驟②:采用奇異值分解的方法,對矩陣R進行分解,得到對應的特征值和特征向量,并降序進行組合排列。
步驟③:對于M個特征值,采用信息論準則(MDL)[18]進行理論上多徑數N的估計。理想情況下,應該只有按照降序排列的前N個特征值為非零值,剩余的M-N個特征值應均為零。考慮到樣本個數有限,最小的M-N個特征值接近零但不相等,并與前N個特征值差距較大,可根據MDL進行判定確定N。
步驟④:得到N的估計值后,構造其他M-N個特征值對應的特征向量矩陣EN=[VM-N+1,…,VM]。
步驟⑤:根據式(3)定義的方位向量a(θ,φ),以及步驟④得到的噪聲子空間矩陣EN,構建以θ、φ為變量的二維方位俯仰估計的MUSIC譜函數如下:
(10)
步驟⑥:基于式(10),在θ和φ得到的二維平面上進行搜索,依次得到幅度最大的N個譜峰的位置,進一步對應查找得到方位和俯仰值,即為各個發射源來波方向和俯仰的估計值。
2 仿真評估
首先在2.1節驗證1.2節理論推導的正確性,然后在2.2節針對最常用的圓型陣列,定量仿真評估其在不同徑數和時延下抗多徑測向的能力。
2.1 隨機陣仿真結果
2.1.1 仿真參數設置
信號頻率為100 MHz,采用隨機陣進行仿真,符號數為1 000,過采樣倍數為10,帶內信噪比為10 dB。考慮3徑的情況,設定多徑入射角分別為50°、90°、120°,俯仰角均為0。考慮不同時延和幅度的影響。
2.1.2 仿真結果
(1) 隨機陣列分布在1.5 m×1.5 m的平面上,3徑延時為0、1、2個符號周期。1.5 m×1.5 m范圍內隨機陣列的仿真結果如圖1所示。
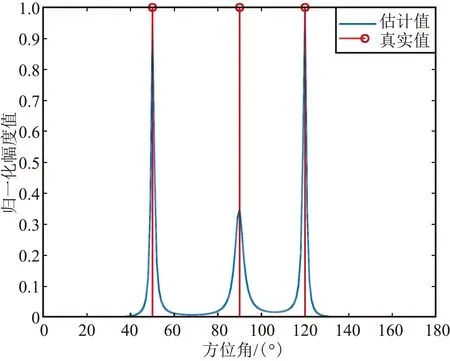
(a)方位估計截面圖
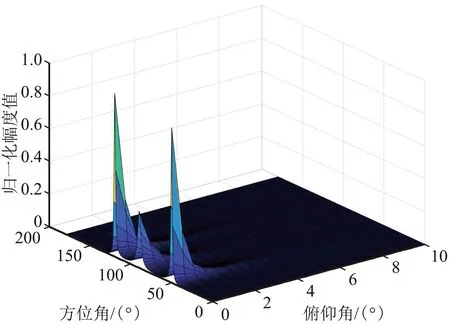
(b)方位/俯仰三維估計圖
(2)分布在0.75 m×0.75 m的平面上,3徑延時為0、1、2個符號周期。0.75 m×0.75 m范圍內隨機陣列的仿真結果如圖2所示。
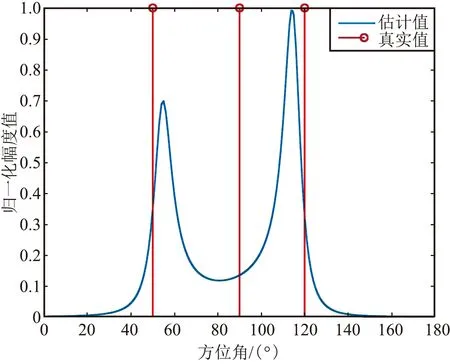
(a)方位估計截面圖
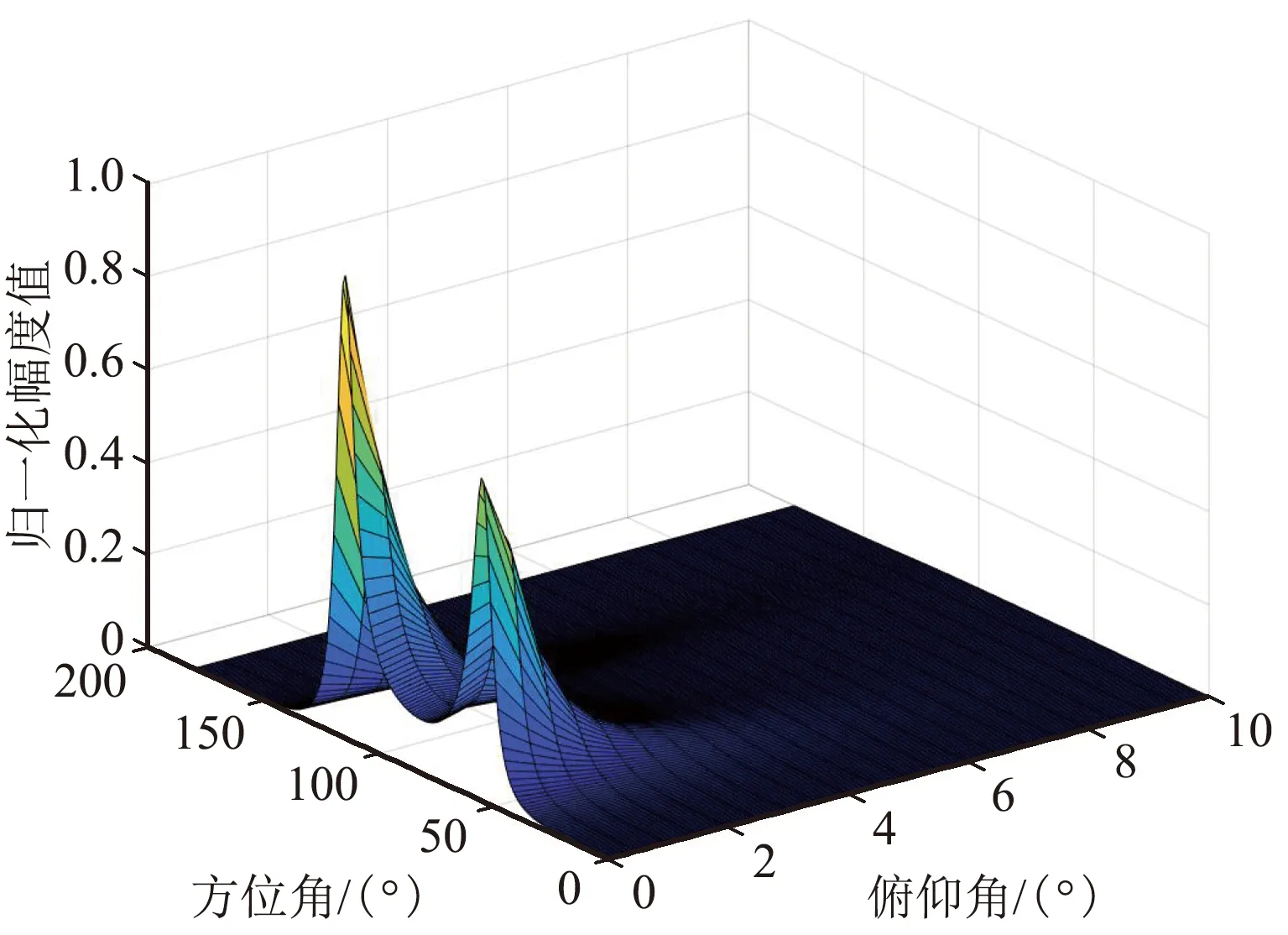
(b)方位/俯仰三維估計圖
從圖1和圖2可以看出,存在多徑時延時,基于MUSIC的空間譜算法也適用,驗證了1.2節推導的正確性。但是,當基線尺度小于0.5倍波長時,會出現估計錯誤的情況。基線的大小對于估計的性能有著顯著的影響。
2.2 圓形陣列性能的定量評估
2.2.1 3徑情況
2.2.1.1 仿真參數設置
信號頻率為100 MHz,采用圓陣進行仿真,圓陣直徑為1 m,接收信號的符號數為1 000,過采樣倍數為10(即每個符號內的采樣點數),帶內信噪比為10 dB。設定多徑入射角分別為50°、90°、120°,俯仰角均為0,3徑的相對幅度設置為1、0.9、0.9,考慮不同時延的影響。
2.2.1.2 仿真結果
① 3徑延時為0、1、2個符號周期
3徑延時為0、1、2個符號周期時仿真結果如 圖3所示。
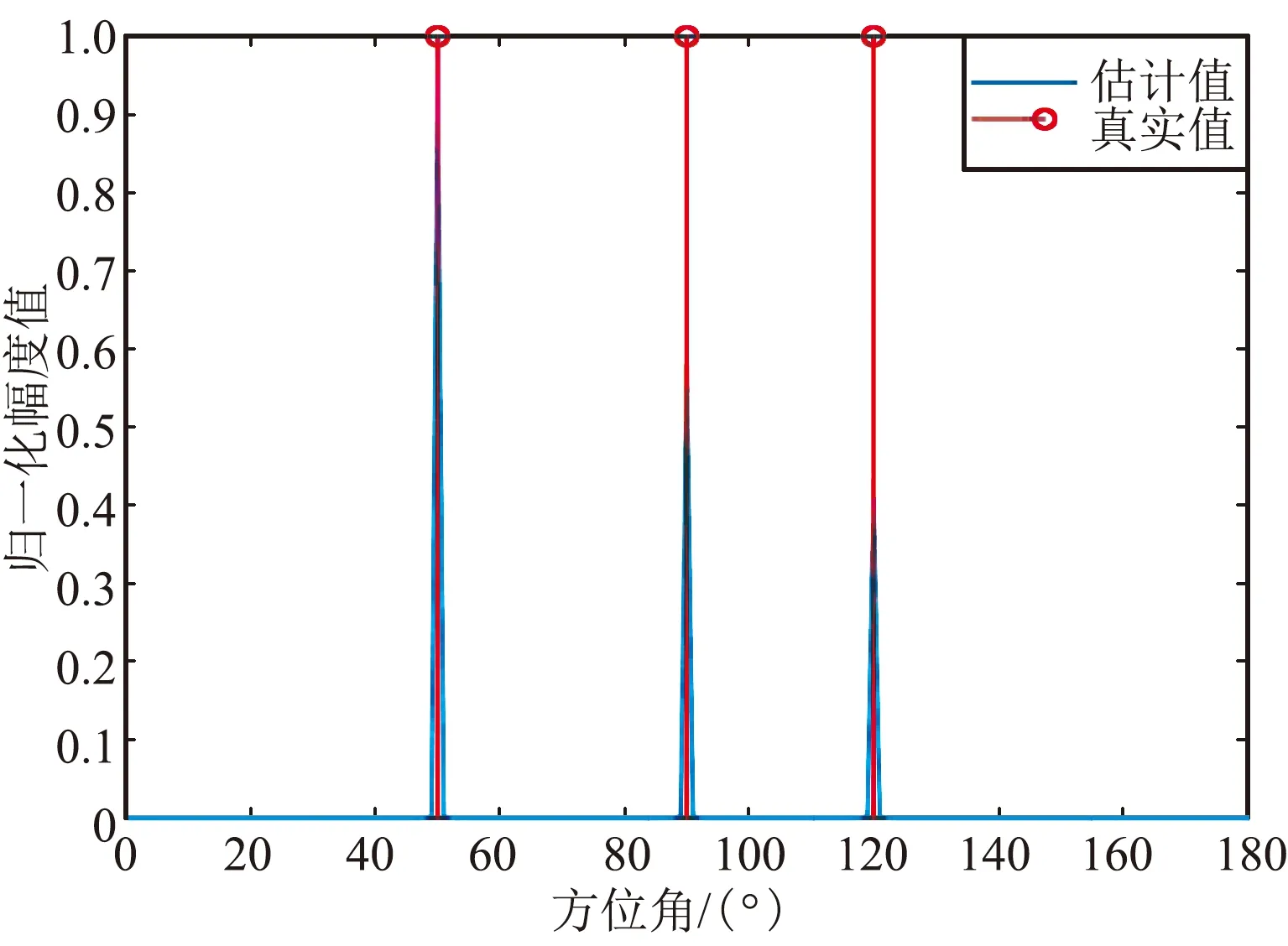
(a)方位估計截面圖
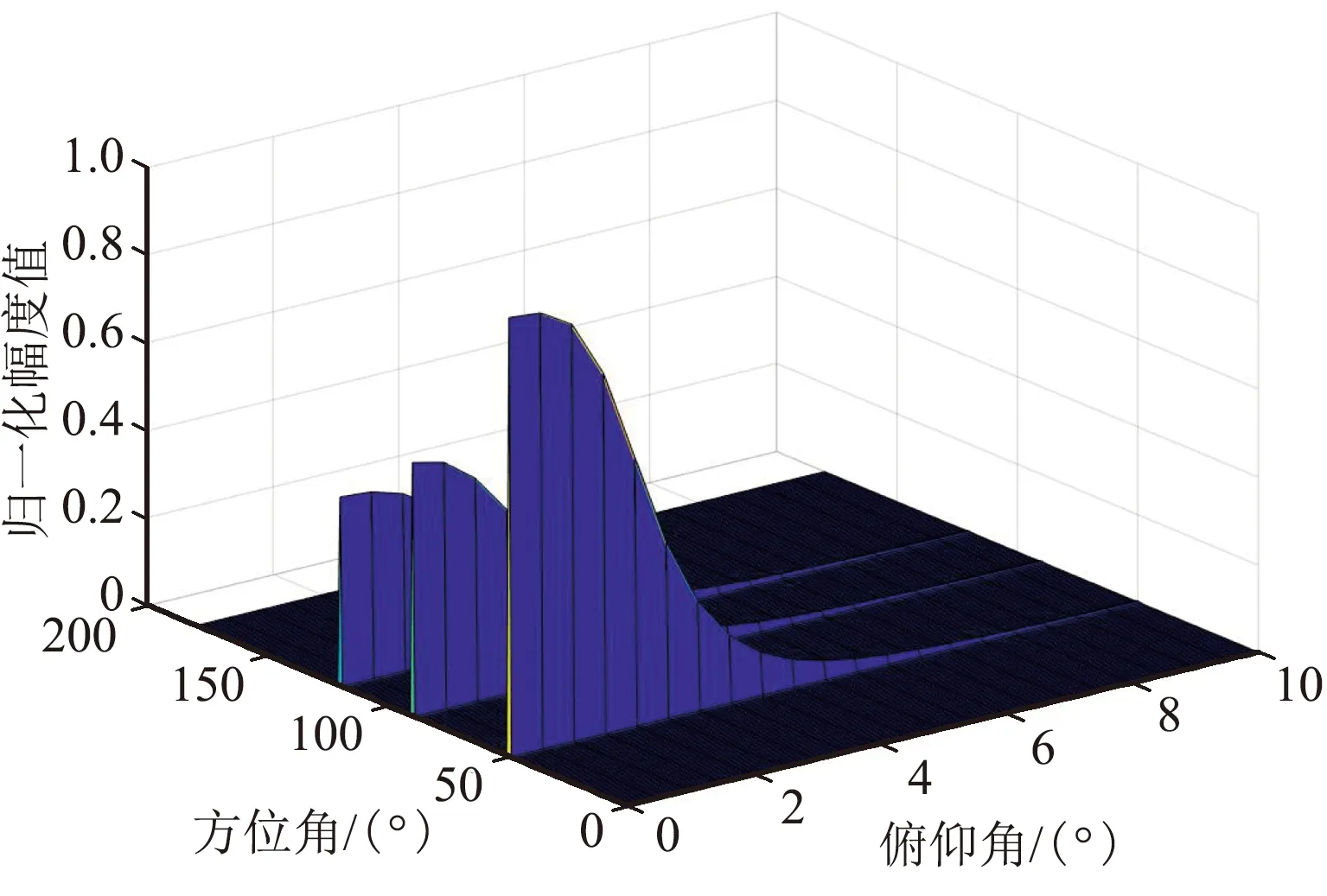
(b)方位/俯仰三維估計圖
② 3徑延時為0、0.4、0.8個符號周期
3徑延時為0、0.4、0.8個符號周期時仿真結果如圖4所示。
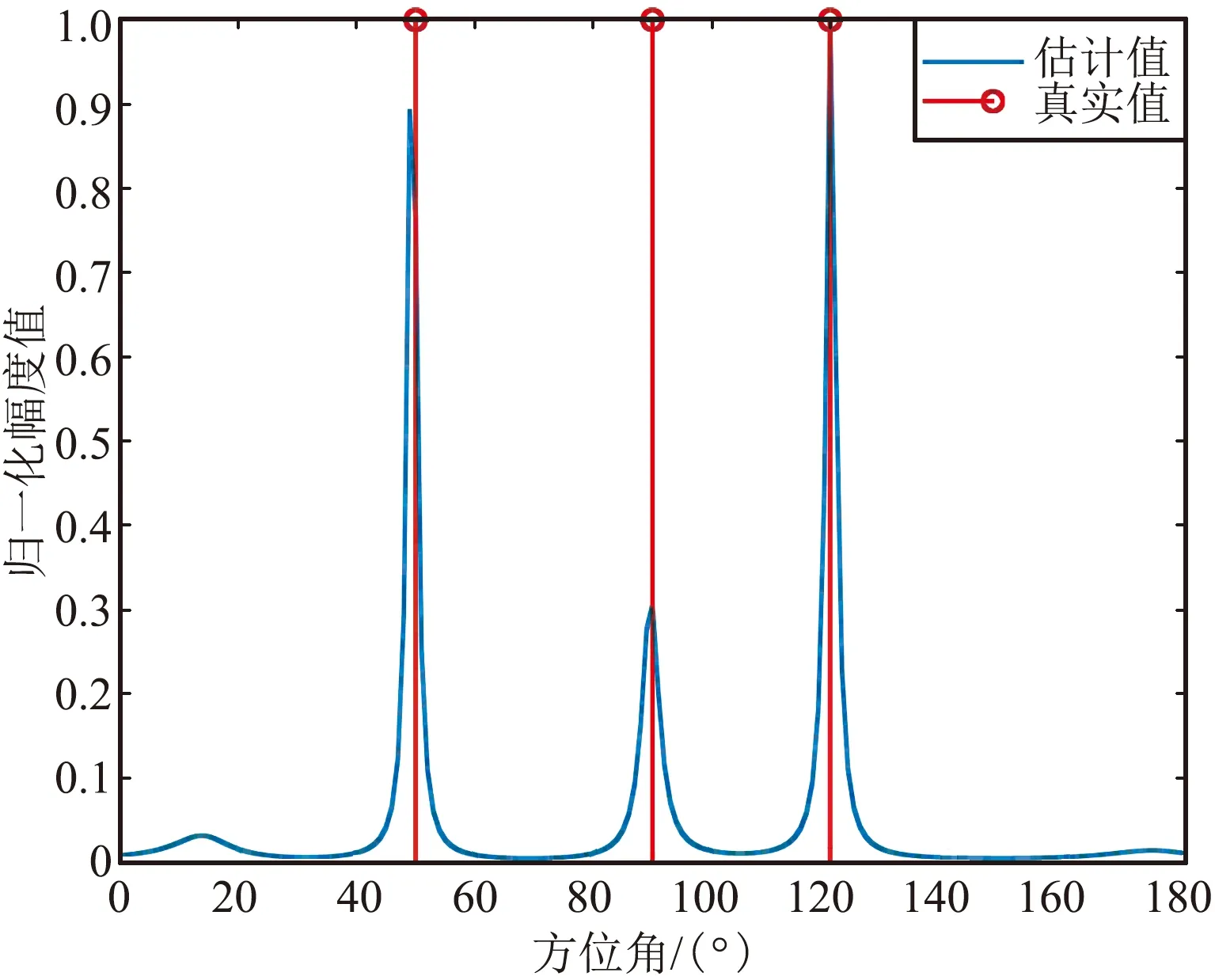
(a)方位估計截面圖
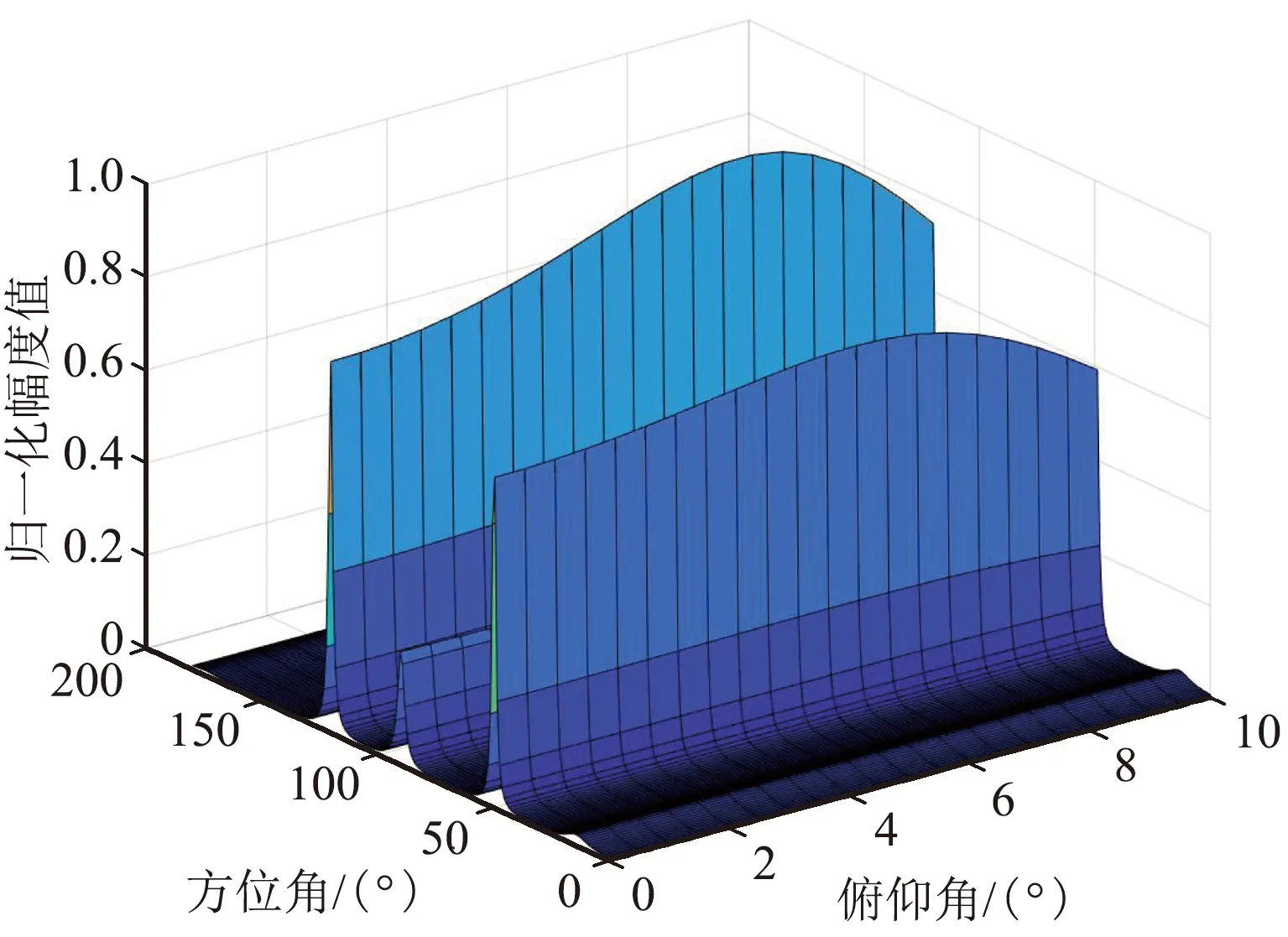
(b)方位/俯仰三維估計圖
③ 3徑延時為0、0.3、0.6個符號周期
3徑延時為0、0.3、0.6個符號周期時仿真結果如圖5所示。
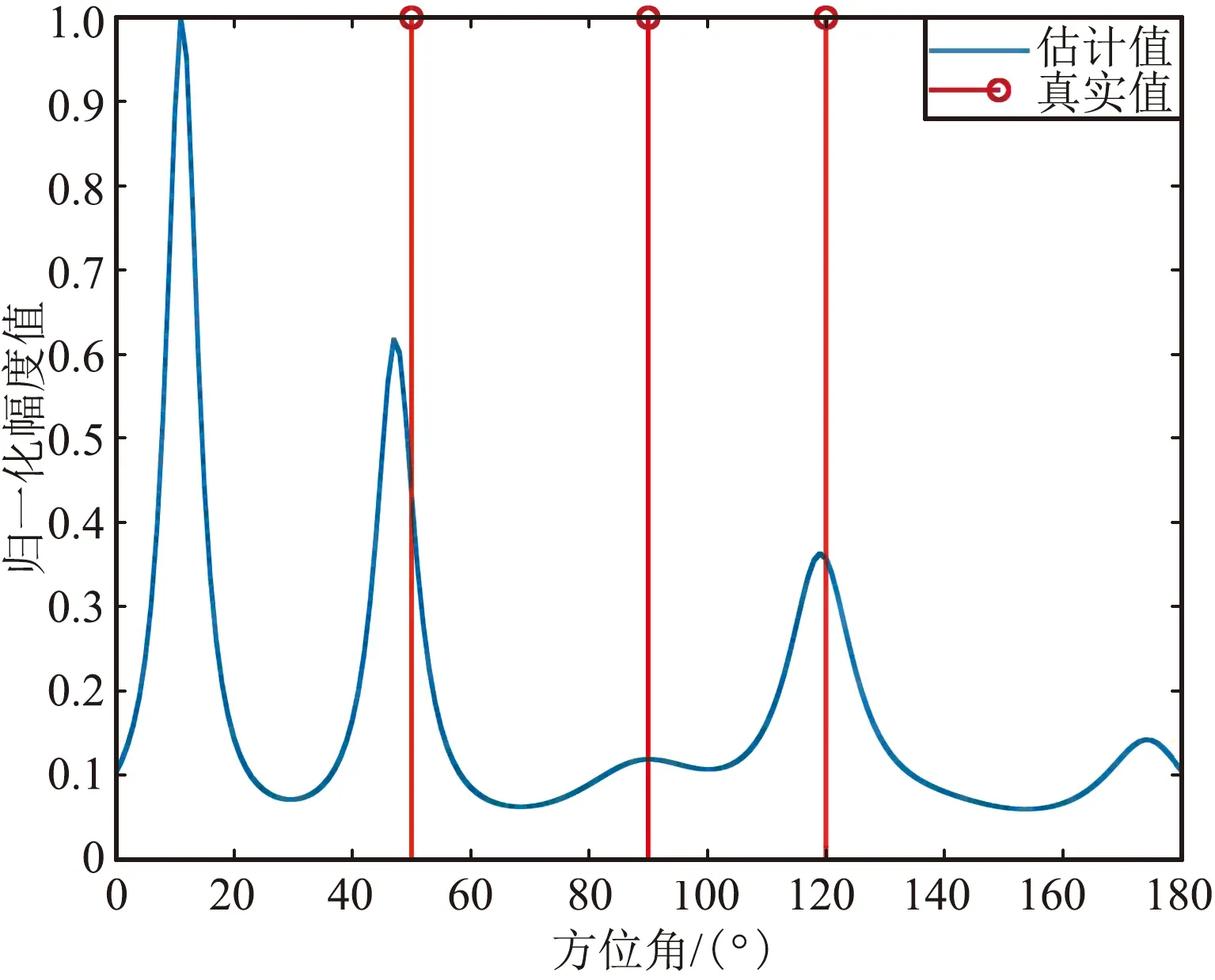
(a)方位估計截面圖
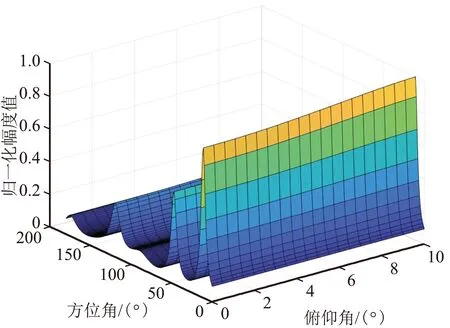
(b)方位/俯仰三維估計圖
從上面的仿真結果可以看出,第一組仿真的時延分別為0、1、2個符號周期時,主徑和另外2個多徑的波達方向估計基本正確,俯仰值的估計也符合設定值;第二組的仿真時延進一步縮小到0、0.4、 0.8個符號周期時,方位和俯仰的估計值基本正確;但是,當第三組的仿真時延進一步縮小到0、0.3、 0.6個符號周期時,對應仿真時延為0.3的波達方向估計錯誤,且影響了時延為0時50°波達方向的估計誤差,估計結果可靠性顯著降低。因此,可以得出初步結論,在3徑的情況下且信噪比較好時,若多徑時延大于0.3~0.4個符號周期,且角度區分度較大時,多徑的波達方向是可分的,此時估計結果的準確性和可靠性較高。
2.2.2 4徑情況
2.2.2.1 仿真參數設置
信號頻率為100 MHz,采用圓陣進行仿真,圓陣直徑為1 m,接收信號的符號數為1 000,過采樣倍數為10(即每個符號內的采樣點數),帶內信噪比為10 dB。設定多徑入射角分別為50°、90°、120°、150°,俯仰角均為0,4徑的相對幅度設置為1、0.9、0.9、0.9,考慮不同時延的影響。
2.2.2.2 仿真結果
① 4徑延時為0、1、2、3個符號周期
4徑延時為0、1、2、3個符號周期時仿真結果如圖6所示。

(a)方位估計截面圖
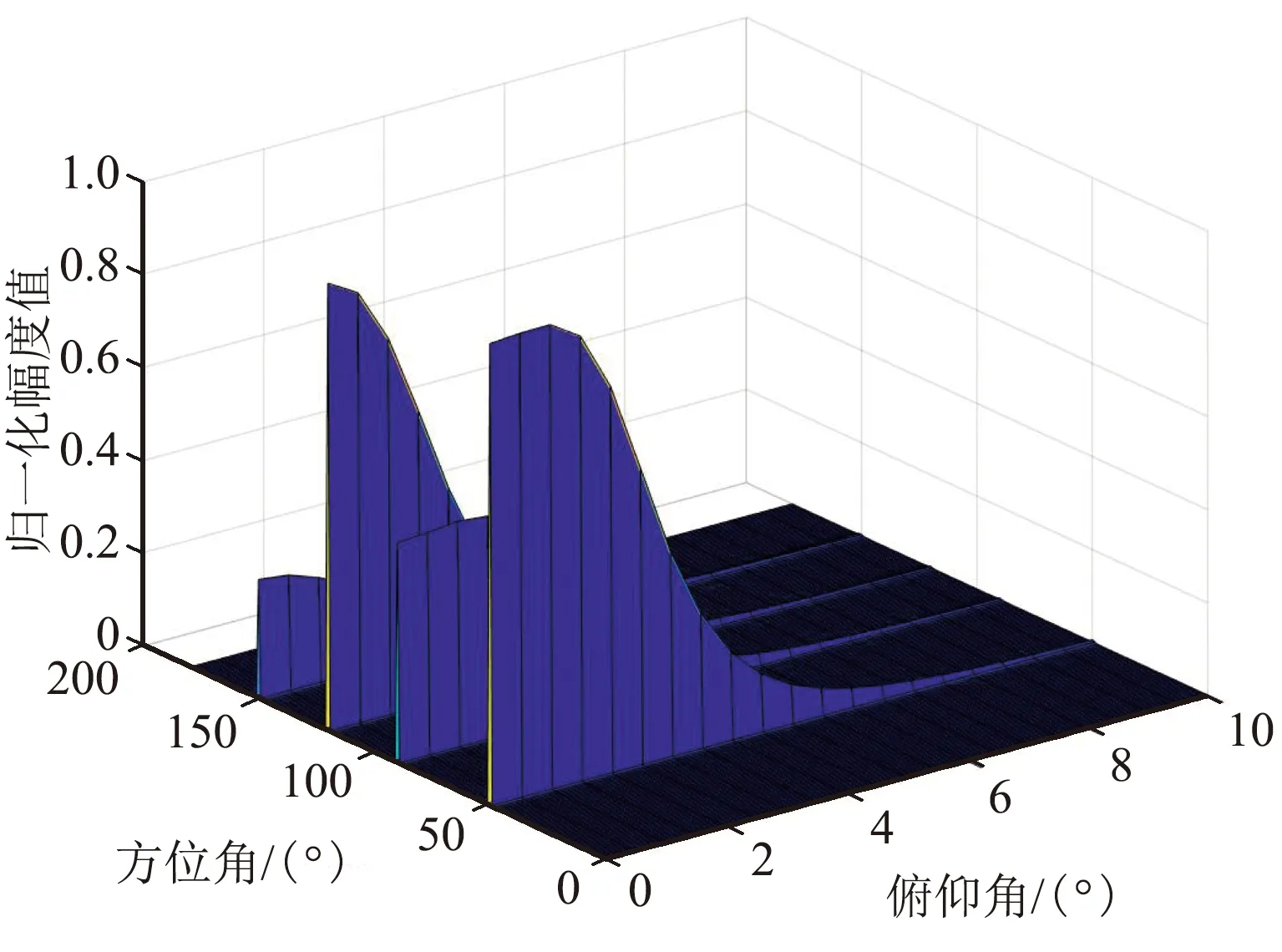
(b)方位/俯仰三維估計圖
② 4徑延時為0、0.5、1.0、1.5個符號周期
4徑延時為0、0.5、1.0、1.5個符號周期時仿真結果如圖7所示。
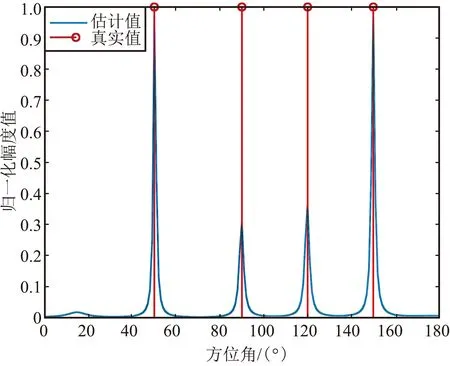
(a)方位估計截面圖
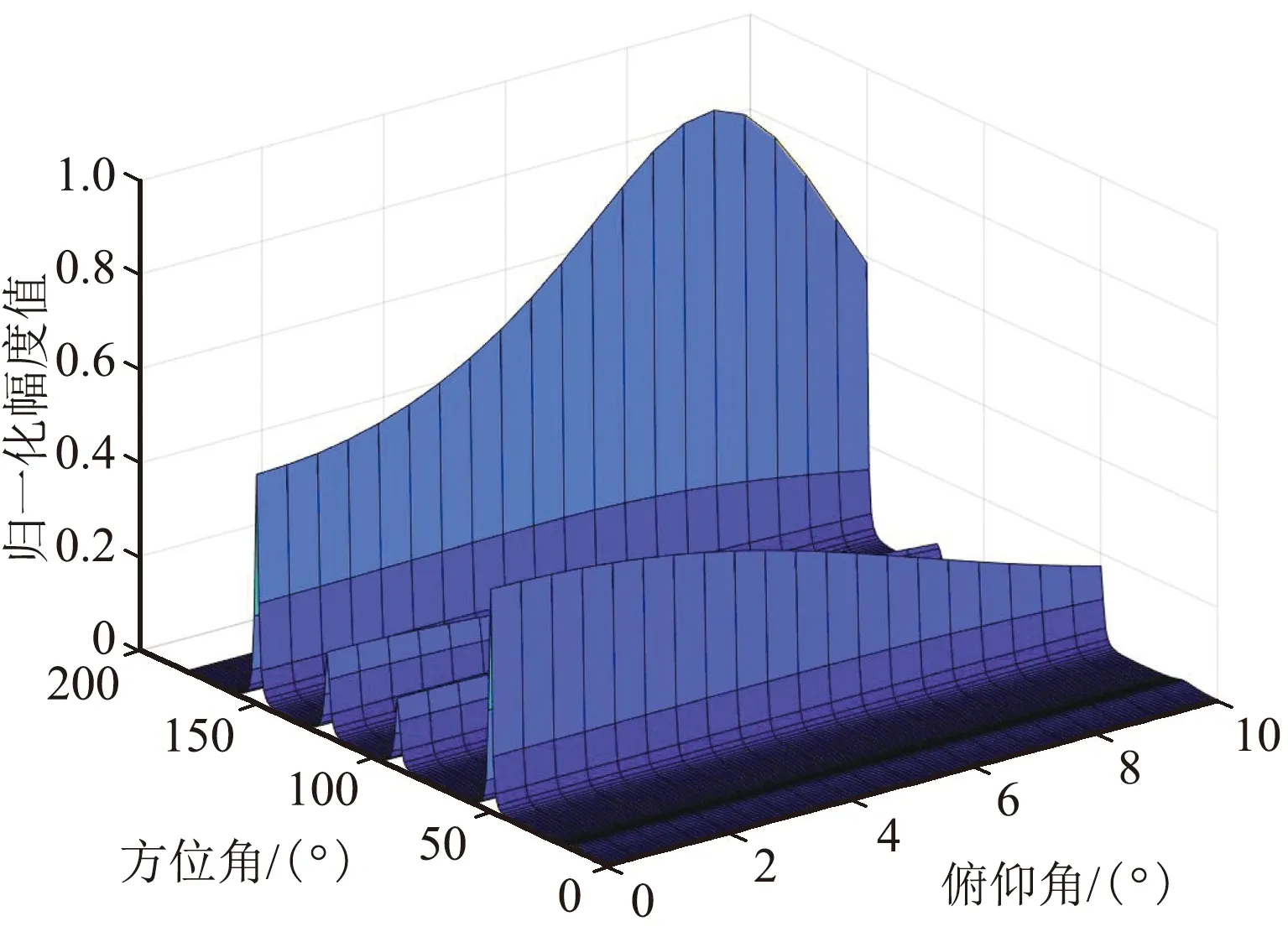
(b)方位/俯仰三維估計圖
③ 4徑延時為0、0.4、0.8、1.2個符號周期
4徑延時為0、0.4、0.8、1.2個符號周期時仿真結果如圖8所示。
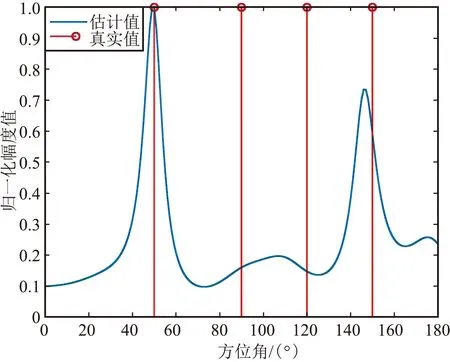
(a)方位估計截面圖
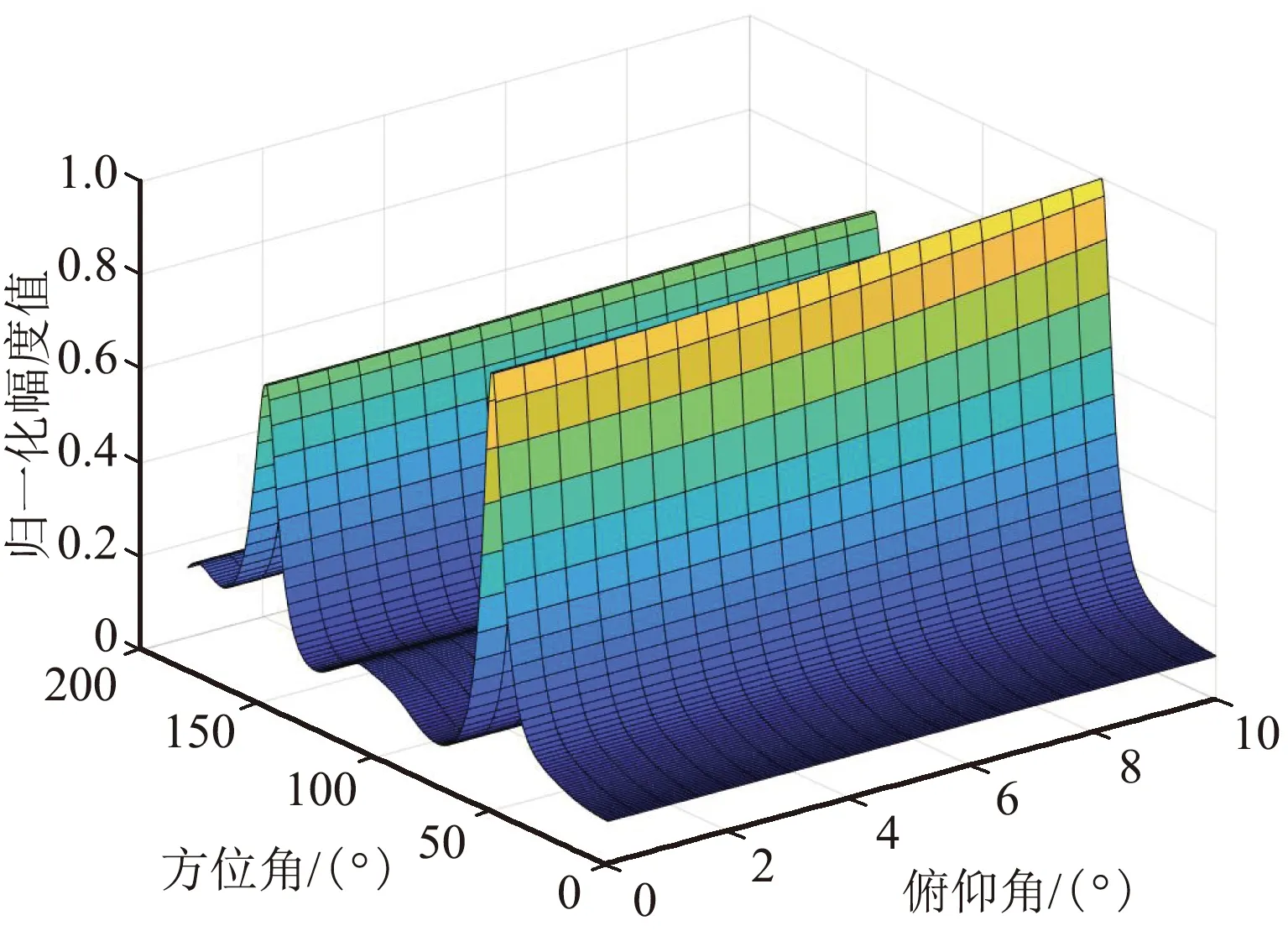
(b)方位/俯仰三維估計圖
從上面的仿真結果可以看出,與2.2.1節的情況基本相似,第一組仿真的時延分別為0、1、2、3個符號周期時,主徑和另外3個多徑的波達方向估計基本正確,俯仰值的估計也符合設定值;第二組的仿真時延進一步縮小到0、0.5、1.0、1.5個符號周期時,方位和俯仰的估計值基本正確;但是,當第三組的仿真時延進一步縮小到0、0.4、0.8、1.2個符號周期時,對應仿真時延為0.4、0.8個符號周期的波達方向估計錯誤,且影響了時延為1.2個符號周期對應的150°波達方向的估計誤差,估計結果可靠性顯著降低。因此,可以得出初步結論,在4徑情況下信噪比較好時,若多徑時延大于0.4~0.5個符號周期,且角度區分度較大時,多徑的波達方向是可分的,估計結果的準確性和可靠性較高。同時,對比2.2.1節的結論可以看出,隨著多徑數的增加,在同樣時延下的估計效果也會變差。
基于上述仿真結果,可以考慮針對性設計實現智能化的多徑測向結果剔除策略,通過采用深度學習網絡等AI技術,對不同徑數、不同時延下多徑的峰值進行仿真分析,得到主徑峰值的出現規律知識庫,從而實現主徑的自動判斷,提升系統的自動化水平。
3 結束語
本文研究了典型測向陣列抗多徑的性能。首先通過理論推導和仿真驗證了多徑信號的測向可分離性,其次重點針對最為典型的圓型測向陣列,通過仿真定量研究了不同多徑數和不同時延下的多徑信號分離測向性能。可以看出,多徑數越多,進行分離測向的難度越大,同時,在非主徑的時延減小時,分離效果顯著降低。本文的研究可以為存在多徑傳播的復雜場景下的多徑信號的分離和直射徑的準確測向提供一定的借鑒。

