基于UE4的電子試驗場區設備電磁干擾分析

郭海亮，陳金勇，張 維，郭國君，杜 明

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

隨著科技裝備和信息化的迅猛發展,復雜電磁環境已成為信息化的重要特征之一。在應對復雜電磁環境下的電子裝備適應性試驗和基地化訓練時,構建和應用電磁環境的水平成為評估訓練成效的關鍵要素。為此,基于信息化時代的電子試驗場已初步具備構建復雜電磁環境的能力。然而,隨著技術的不斷提升,仍需進一步提高復雜電磁環境構建方法、條件等方面的專業化、標準化和精細化水平。這將有助于更準確地模擬戰場上的復雜電磁環境,進一步提高訓練的實用性和效果評估的可靠性。

針對電磁環境和設備建模的研究有很多。文獻[1-2]以電磁干擾預測方程為基礎,構建電磁兼容系統發射機模型和接收機模型。文獻[3]定義了電磁干擾余量 (Interference Margin,IM),進行系統間電磁兼容預測分析。文獻[4-5]研究了電磁兼容中的電磁干擾發射機原理,建立基于發射機模型的基波、諧波、非諧波和互調模型。文獻[6]將接收機模型分為敏感度模型、頻率選擇性模型、亂真響應模型、互調模型和減敏模型,建立了接收機模型,定義了接收機的敏感度門限。文獻[7]針對接收機內的非線性問題,以及多個干擾信號在接收機前端發生混頻或其諧波分量發生混頻的問題,建立了接收機互調模型。文獻[8]構建了對電波傳播路徑的損耗模型。文獻[9]根據不同地質建立了地波傳播模型。

針對電磁干擾分析的研究也有很多。文獻[10]基于傳統分級篩選法提出了一種新穎的車載通信系統電磁干擾預測方法。文獻[11]只考慮干擾發射機和接收機的功率幅度,并采用自由空間傳輸模型,剔除未對接收機造成干擾的發射機。文獻[12]根據GJB 8848—2016對關鍵通信設備的要求,將車載接收機的干擾余量限值定為-6 dB。文獻[13]發現色散的原因在于高頻部分,從而提出了SF-FDTD算法,將高頻成分濾除來突破Courant-Friedrichs-Lewy (CFL)穩定條件。文獻[14]利用Keller繞射分解固定形狀的繞射錐束,提高了追蹤效率。文獻[15-17]針對現實高鐵環境進行了傳播測量和建模,彌補了經驗模型和隨機模型的局限性。文獻[18]基于LabVIEW軟件對發射機對中可能存在的干擾問題進行了預測和分析。

電子裝備適應性試驗與基地化訓練在復雜電磁環境中進行,電磁環境的構設與應用水平對于評估訓練效果至關重要。電子試驗場已初步具備構建復雜電磁環境的能力,然而,當前技術的不斷提升帶來了新的挑戰。現有的靜態仿真模型構建技術無法準確實現復雜電磁環境下設備的仿真、模擬等工作,且相應的干擾分析技術并不完善,無法有效綜合利用各參試設備模型、場地環境模型、設備具體布設位置和設備架設高度等信息實現較為精準的干擾分析,因此如何對設備、電磁環境和地理環境等靜態模型進行細致建模并以此模型結合真實環境下設備及環境相關信息實現試驗場區干擾分析仿真,是研究的重中之重。

針對以上問題,提出了一種大型綜合電子試驗場電磁環境建模與電磁干擾分析技術,主要貢獻如下:

①綜合考慮所采取的干擾分析方法,所建立的設備和環境模型能全面反映干擾分析所需參數。各參試設備模型需綜合考慮近場和遠場區域。針對設備模型近場區域,采用時域有限差分算法計算用頻設備近場區域場分布,分析發射設備對近場范圍內接收設備的影響。針對設備模型遠場區域,綜合考慮設備頻譜特性,根據干擾計算需求,建立基于設備的典型性能指標模型。同時根據三維地理模型建立相應環境模型,準確描述電磁波在該環境的反射、透射和散射等情況,所建模型及各模型參數基于Unreal Engine 4 (UE4)平臺進行可視化展示。

②場區相互作用及干擾分析可最大程度反映場區內各試驗能否兼容運行,并提供空間、時間、頻率建議調整方案。因此建立電磁干擾分析模型,基于各種用頻規定、周邊電磁環境數據以及實際經驗數據等信息,結合各參試設備模型、場地環境模型、設備具體布設位置和設備架設高度等信息,運用各種干擾仿真分析方法,并提出一種基于設備空間位置的時域有限差分(Finite Difference Time-Domain,FDTD)網格劃分方法,進行場區內設備的相互作用和干擾分析。同時需分析單項試驗設備通信可視性、通信覆蓋范圍等。

1 系統模型

系統模型主要分為設備模型和環境模型,其中設備模型分為發射機模型和接收機模型,并在UE4平臺進行可視化展示。UE4是美國Epic游戲公司研發的一款3A級次時代游戲引擎[19]。由于其強大的開發能力和開源策略,UE4除了在游戲行業被使用外,還被廣泛應用到視頻制作行業、影視行業、直播娛樂行業、軍事訓練、汽車設計和建筑室內設計行業等。

1.1 設備模型

發射機模型:主要研究不同試驗設備間的相互干擾,因此將干擾設備與發射設備統稱為發射機。發射機在工作過程中,產生正常工作信號的同時,還會在某些頻率上產生輻射信號,比如諧波輻射和亂真輻射。這些輻射信號落在接收機帶寬范圍內會對接收機造成諧波干擾或亂真干擾。因此,在建立發射機模型的過程中,需要考慮發射機的發射功率、頻率、增益和帶寬等參數。對此,建立了發射機基波輻射模型和發射機諧波輻射模型。圖1為基于UE4的發射機模型。

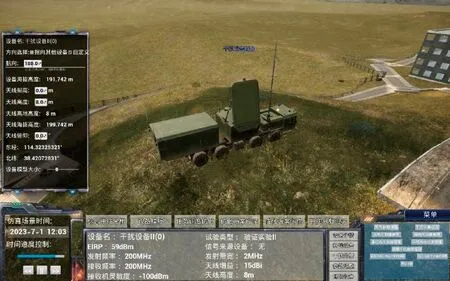
圖1 發射機模型Fig.1 Transmitter model

①發射機基波輻射模型

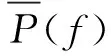
(1)

(2)

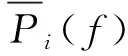
②發射機諧波輻射模型

發射機諧波輻射主要是由發射機內部器件的非線性導致的,諧波輻射分量的頻率是基波頻率的整數倍,且隨著倍數的增加,功率逐漸減小。諧波功率變化也服從正態分布,標準偏差與諧波次數無關,其諧波輻射幅度模型為:

(3)

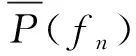
表1 發射機諧波輻射模型參數Tab.1 Parameters of transmitter harmonic radiation model

接收機模型:實際情況下接收機除了接收目標信號外,還會接收到某些帶外干擾信號。對此,考慮接收機模型為敏感度模型、亂真響應模型。圖2為基于UE4的接收機模型。

圖2 接收機模型Fig.2 Receiver model

①接收機敏感度模型

接收機靈敏度通常由接收機的噪聲電平來表示。接收機靈敏度和噪聲系數、工作帶寬和溫度等因素有關,計算如下:

S=kTFBR,

(4)

式中:S為接收機基波靈敏度,單位dBm;k為玻爾茲曼常數;T為絕對溫度,單位K;BR為接收機工作帶寬,單位Hz;F為接收機噪聲系數,單位dB。

②接收機亂真響應模型

接收機亂真響應是指接收機帶外干擾信號與接收機本振信號發生混頻產生的干擾,從而使接收機產生亂真響應。

接收機的亂真響應模型與發射機諧波輻射模型類似,平均亂真響應敏感度門限模型可表示為:

S(fp)=S(f)+I×lgp+J,

(5)

式中:S(fp)為接收機對諧波的靈敏度,單位dBm;S(f)為接收機對基波信號的靈敏度,p為諧波次數,I、J為接收機經驗常數。通用參數如表2所示。

表2 接收機亂真響應模型參數Tab.2 Parameters of receiver spurious response model

1.2 環境模型

環境模型是根據三維地理模型建立的,環境中物體的材質會影響到其介電常數和復電導率等信息,進而影響到電磁波的反射、繞射和散射系數。總體仿真場景如圖3所示。

圖3 總體仿真場景Fig.3 Overall simulation scenario

電磁計算流程如圖4所示。環境模型根據電磁波波長劃分為近場區域和遠場區域,針對設備模型近場區域,綜合考慮邊界條件,采用計算電磁學算法,如FDTD法等,計算該用頻設備近場區域場強分布,分析發射設備對近場范圍內接收設備的影響。針對遠場區域,綜合考慮用頻設備的頻譜特性,根據干擾計算需求,建立基于設備的典型性能指標的模型,通過對信號傳播的路徑損耗、多徑時延和空間分布等進行計算,得到接收端信號關鍵參數的變化,進而可以用于設備之間的干擾分析。

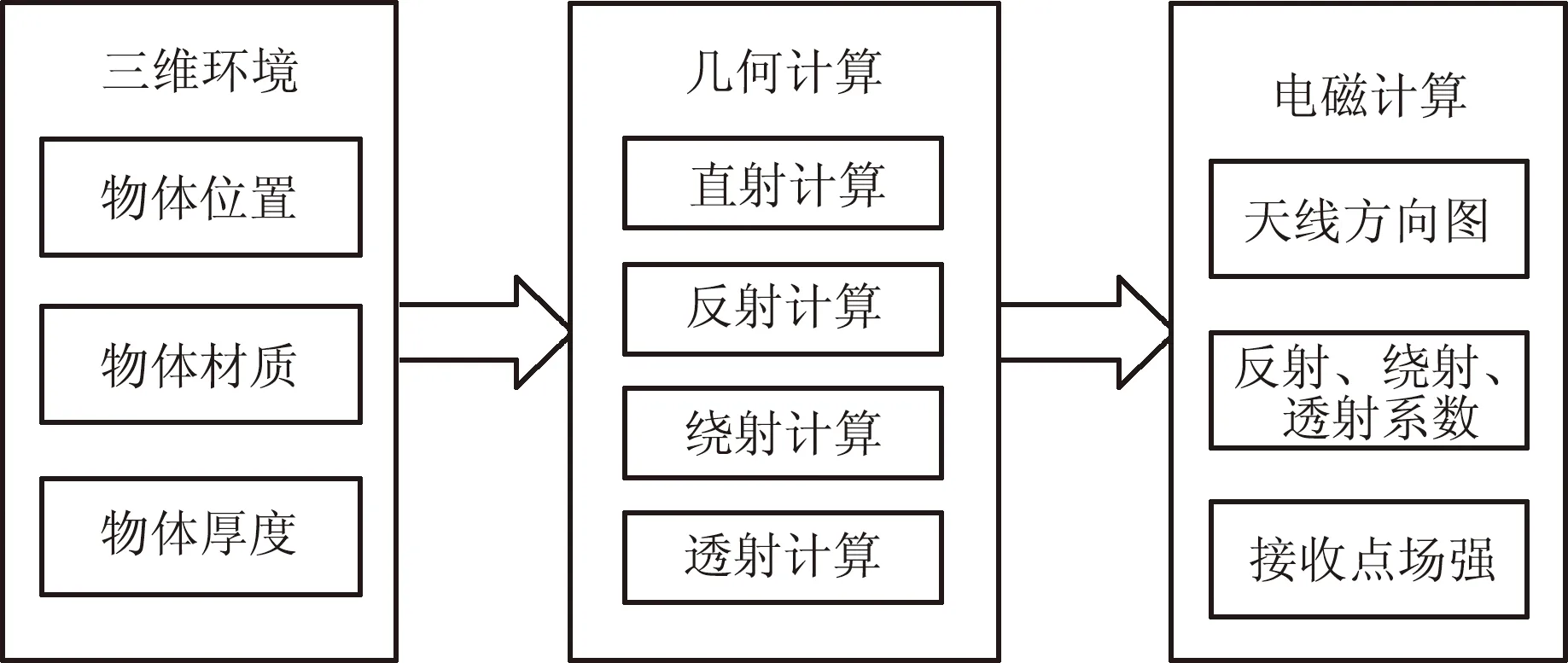
圖4 電磁計算流程Fig.4 Electromagnetic calculation process

電磁輻射區的劃分計算如下:

(6)

式中:λ為波長,D為天線最大尺寸,單位m;R為輻射區劃分界限,單位m。當輻射距離大于R時,劃分為遠場,反之劃分為近場。

在實際電磁波傳輸環境中,由于通信設備之間有一定的距離,當設備收發天線處于對方遠場區時,必須考慮空間的傳輸損耗。因而需要對常見環境下的電波傳播損耗進行建模分析。

①自由空間傳播

工程上常用的自由空間傳播損耗公式如下:

Lbf=32.4+20 lgf+20 lgd,

(7)

式中:f為信號頻率,單位MHz;d為收發天線的距離,單位km。

②擴展Hata模型

實際測試環境為郊區環境,相對空曠, Okumura-Hata模型較為適用,符合場景預期。在此基礎上,選擇采用擴展Hata模型,其基本傳播損耗公式為:

(8)

式中:

F(h1,d)=(44.9-6.55 lgh1)lgd,

(9)

h1為發射機天線有效高度,h2為接收機天線有效高度,α(h2)為接收天線高度修正因子。

(10)

在郊區或鄉村環境下,損耗模型變化如下:

2 干擾分析方法

2.1 電磁干擾原理分析

在通信系統電磁干擾預測中,將電磁干擾源和敏感設備分別統稱為發射機和接收機,將干擾源耦合到敏感設備上的干擾功率大小統稱為干擾量。通過比較發射機作用于接收機的有效干擾功率和接收機的敏感度門限,可以確定系統是否存在潛在的電磁干擾環境。接收機的受擾程度可以用干擾余量來描述:

IM(f,t)=PE-S(f),

(12)

式中:IM(f,t)為接收機的干擾余量,單位dB;PE為發射機耦合到接收機天線端口的有效干擾功率,單位dBm;S(f)為接收機的靈敏度,單位dBm。

接收機天線端口的有效干擾功率計算如下:

PE=P(f)+Gtx(θtx,φtx)-L(f,d)+Grx(θrx,φrx),

(13)

式中:PE為接收機前端的干擾功率,單位dBm;P(f)為發射機基波和雜散發射功率,單位dBm;Gtx(θtx,φtx)為發射天線在接收方向的增益,單位dB;Grx(θrx,φrx)為接收天線在發射方向的增益,單位dB;L(f,d)為傳播損耗,單位dB。

當接收機接收到多個干擾源的干擾信號時,接收機干擾余量的計算如下:

(14)

式中:Pi為第i臺干擾發射機對接收機造成的有效干擾功率。

在電磁干擾分析系統中,當IM>0時,表示系統受到干擾;IM=0表示系統處于臨界干擾,無法確定是否存在電磁干擾環境;IM<0表示系統處于兼容狀態,不存在電磁干擾環境。

2.2 干擾分析流程

電磁干擾分析中,根據空間、時間和工作頻率等因素對所有發射機進行篩選,以確定潛在的干擾源。首先從時間和空間上對發射機進行篩選,如果發射機和接收機工作時間同步或空間布局擁擠,說明可能存在EMI環境,把這部分可能對接收機造成干擾的發射機保留下來,建立干擾發射-響應對。

在幅度篩選這一階段,只考慮干擾發射機和敏感接收機的功率幅度電平,并采用路徑傳播模型,對干擾發射-響應組合做進一步分析,排除不會造成干擾的發射機。干擾余量計算方法如下:

基波干擾余量(FIM):

(15)

發射機干擾余量(TIM):

(16)

接收機干擾余量(RIM):

(17)

亂真干擾余量(SIM):

(18)

首先計算FIM,當FIM小于干擾余量限值,表明沒有受到干擾;當FIM超過設定閾值,繼續計算TIM和RIM;當TIM或RIM超過閾值,繼續計算SIM,否則跳過SIM,并進行下一階段的預測分析。

根據干擾發射機輻射的電磁波頻率和發射機到接收機的距離計算路徑傳播損耗,對每個發射-響應對的電磁干擾余量進行計算。

3 干擾分析技術

3.1 改進的FDTD法

FDTD法是一種數值算法,該方法基于Maxwell方程組,通過將Maxwell方程組中的旋度方程用有限差分形式代替微分方程,得到電場和磁場各分量。同時,該方法采用空間網格來模擬研究對象的電磁特性,并選擇適當的場初始值和吸收邊界條件。通過迭代計算空間中的電場和磁場,在一定的時間步長下模擬電磁波的傳播和與物體的相互作用。這樣可以在計算機的數字空間中得到包含時間變量的Maxwell方程的四維數值解,實現對電磁波傳播過程的時域模擬計算。

首先,將空間分成很多網格單元,用Δx、Δy、Δz分別表示在x、y、z坐標方向的網格空間步長:(i,j,k)=(iΔx,jΔy,kΔz)。

令f(x,y,z,t)代表電場或磁場的某一分量,在時間和空間域中的離散表示如下:

f(x,y,z,t)=f(iΔx,jΔy,kΔz,nΔt)=fn(i,j,k)。

(19)

以x方向場強為例,經過中心差分后的離散方程為:

(20)

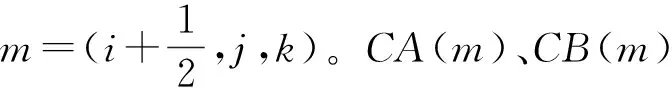
式中:ε(m)、σ(m)、μ(m)為對空間的媒質特性進行描述,Δt為時間步長。

在劃分網格區域的過程中,結合發射機和接收機實際空間位置,將激勵源和接收源設置在仿真區域邊緣,減少仿真網格數量,同時節省了仿真計算資源,加快了仿真速度。z軸等于0。簡要二維平面示意如圖5所示。

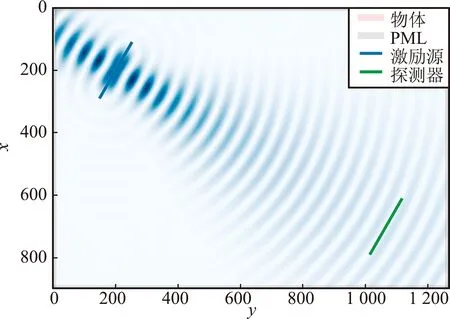
(a)激勵源位于上方

以20 m距離為例,藍色長條為激勵源,綠色為探測器。圖5(a)為激勵源在探測器上方的位置,此時劃分網格時會自動適應激勵源和探測器的位置,將二者放在仿真區域2個角落邊緣。圖5(b)為激勵源位于探測器下方位置的情形。

同時,為防止仿真造成的邊緣反射,在添加完美匹配層(PML)的同時,將發送源和接收源放置在仿真區域的2個角落,盡可能減少仿真資源。此外,為防止激勵源和接收器落在仿真區域外圍的PML,將二者分別遠離PML至少2個波長,減小不必要的誤差。

3.2 射線跟蹤法

繞射定律描述了繞射點的位置和繞射射線的方向。根據繞射定律,如果繞射射線和入射射線在同一介質中傳播,則它們與繞射點所在的邊之間形成相同的夾角,并且分布在垂直于繞射點所在邊的平面的兩側。當入射射線以斜角照射邊時,繞射射線將形成一個錐形;當入射射線以垂直角度照射邊時,繞射錐將退化為圓盤形狀。

幾何繞射理論對幾何光學進行了重要修正,使其成為高頻計算的關鍵方法。幾何繞射理論能夠計算陰影區域的場景,但在計算陰影邊界的過渡區域時,繞射公式可能會產生奇異性。為解決這一問題,Kouyoumjian和Pathak提出了一致性繞射理論,通過在繞射系數中引入過渡函數,確保繞射場在穿越陰影邊界時仍保持有界。在陰影邊界上,過渡函數和繞射系數以相同的速率趨近于零,從而得到有界的繞射場。

當幾何光學射線遇到任何形式的表面不連續,例如邊緣、尖頂或斜角入射曲面時,將形成無法進入的陰影區域。幾何光學理論無法計算陰影區域的場景,并且其在陰影邊界附近的場景計算結果也不準確。通過深入研究繞射現象,提出了邊緣繞射射線的概念,以修正幾何光學無法計算陰影區域場景的缺點,并擴展了幾何光學的應用范圍,形成了幾何繞射理論。

①反射電磁計算

入射電波存在2種不同的極化方式,通常將電波分解為水平極化波分量和垂直極化波分量,分別對應水平極化和垂直極化。入射面是入射射線與垂直于入射面法線方向且經過反射點的射線所構成的平面。其中電波在傳播過程中極化方向平行于入射面的電場分量稱為平行極化波分量,極化方向垂直于入射面的電場分量稱為垂直極化波分量。假設反射點為Q,接收點為S,則場點S處的反射波末場為:

hr(S)=hi(Q)·R·A(s)·e-jks,

(23)

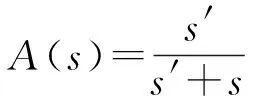
(24)

式中:R⊥和R∥分別為垂直極化、平行極化的反射系數。

(25)

(26)

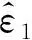
(27)

式中:ε為介電常數,σ為反射面的電導率,ω為角頻率。

②繞射電磁計算

繞射射線用幅度、相位和極化來描述,在繞射點處的入射電場乘以繞射系數、擴散因子和一個相位項,假設P為繞射射線上任意場點,距繞射點M的距離為s。

hd(P)=hi(M)·D·A(s)·e-jks,

(28)

式中:D為繞射系數。在射線基坐標系下可以表示為:

(29)

根據UTD理論,并矢繞射系數為:

(30)

(31)

式中:D⊥為垂直極化波繞射系數,D∥為水平極化波繞射系數,n為楔因子,在90°拐角處為3/2;β0為入射射線與楔的夾角。

(32)

式中:Li、Ld為距離參數,F(x)為過渡函數。

(33)

③透射電磁計算

透射過程由三部分組成:折射入介質、在介質中傳播和折射出介質。假設射線在Q點穿透前路徑總距離為s,則反射波場點Q處的透射波末場與反射點Q處入射波末場的關系為:

(34)

式中:Tin為入射波透射系數,Tout為出射波透射系數,s′為射線在介質中傳播的距離,T為折射系數。

(35)

式中:

(36)

(37)

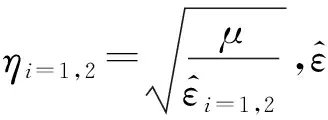
4 仿真結果

本實驗基于UE4平臺搭建大型電子綜合試驗場,針對場區不同類型、不同數量的設備,構建環境基礎仿真模型和設備干擾分析模型。

試驗場區域是總面積為4 km2的不規則區域,考慮地形、房屋、水面和樹木等實際環境,并在UE4平臺中進行三維可視化。

此外,考慮天氣、晝夜等變化因素,即在不同天氣、不同時間的情況下,每種材質的電導率和介電常數也會有變化。表3為常見地質的電參數平均值。

表3 常見地質的電參數平均值Tab.3 Average value of electrical parameters in common geology

根據不同的地表類型,將地表電參數劃分為晴天、陰天和雨天等天氣。一些主要物體的材質及其介電常數和電導率如表4所示。

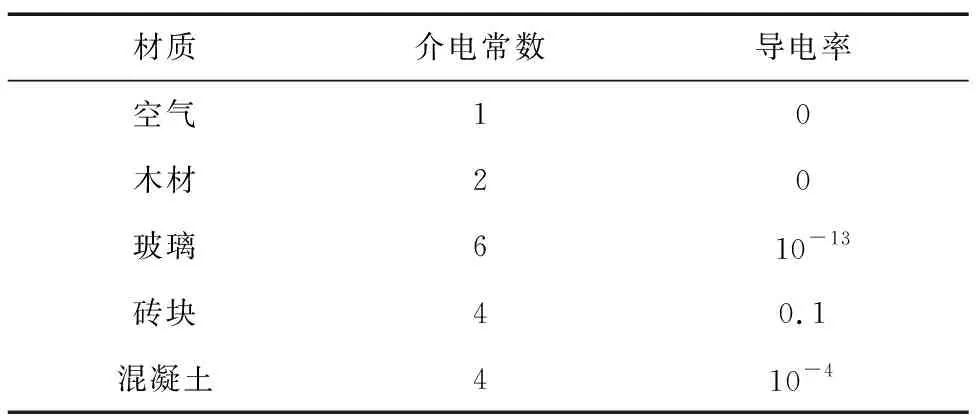
表4 常見材質的電參數平均值Tab.4 Average value of electrical parameters of common materials

針對不同設備種類的實驗類型,將設備模型分為發射機模型和接收機模型,并通過UE4平臺可視化展現。每臺設備模型主要參數包括:天線高度、發射功率、發射頻率、接收頻率、帶寬、接收靈敏度、天線架高、天線增益、極化方式、航向角和俯仰角。其中,航向角以正北方向為參考系。以小型天線為例,具體參數如表5所示。

針對場區存在的不同設備種類,進行不同類型的仿真試驗。由于天線實際增益和發射功率較小,選取10、20 m的距離作為干擾試驗仿真分析距離。圖6為發射天線和接收天線距離10 m的UE4的仿真場景。

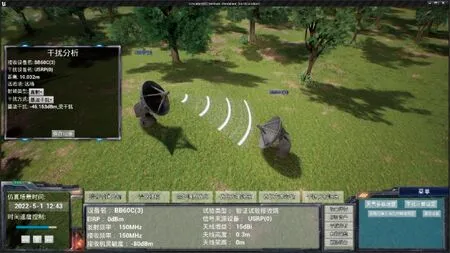
圖6 10 m仿真場景Fig.6 10 m simulation scene diagram

表6為10 m距離的實際場景測量與系統仿真測試的基波干擾余量結果對比。

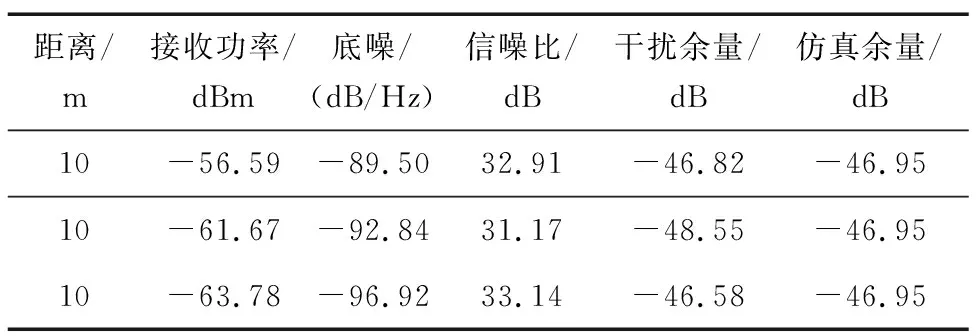
表6 小型天線10 m距離測試Tab.6 10 m distance test of small antenna

從表6可以看出,由于環境的動態變化性,環境底噪也在不斷波動,導致實際測量的接收功率會隨之波動。因此,可通過接收功率和底噪計算出信號的信噪比。接收信號的信噪比雖然也會有一定的小幅度波動,但基本穩定在31～33 dB。由此可以計算出干擾過程中的基波干擾余量,并與系統仿真結果進行對比。

經過3次測量,底噪波動較大,導致接收天線的接收功率變化幅度隨之增大,最大達到7 dB左右,但是信噪比基本穩定。由此可以看出,在實際測量過程中,即使是同一環境也會出現細微的變化,導致實測結果有一定的測量誤差。而仿真系統在相同情況下只可能有一種結果,仿真系統計算出的干擾余量與實際測量結果相比,誤差在0.13～1.6 dB,最小誤差為0.13 dB。

在實際環境中,由于環境的動態多變性,在測量過程中會存在測量誤差,同時,在計算過程中,也有可能出現相應的計算誤差。因此,在進行仿真過程中,需要根據實際環境進行針對性的測量。

為了進一步測量小型天線在更遠距離的仿真情況,將仿真距離提升到了20 m,此時接收信噪比大幅降低,如圖7所示。

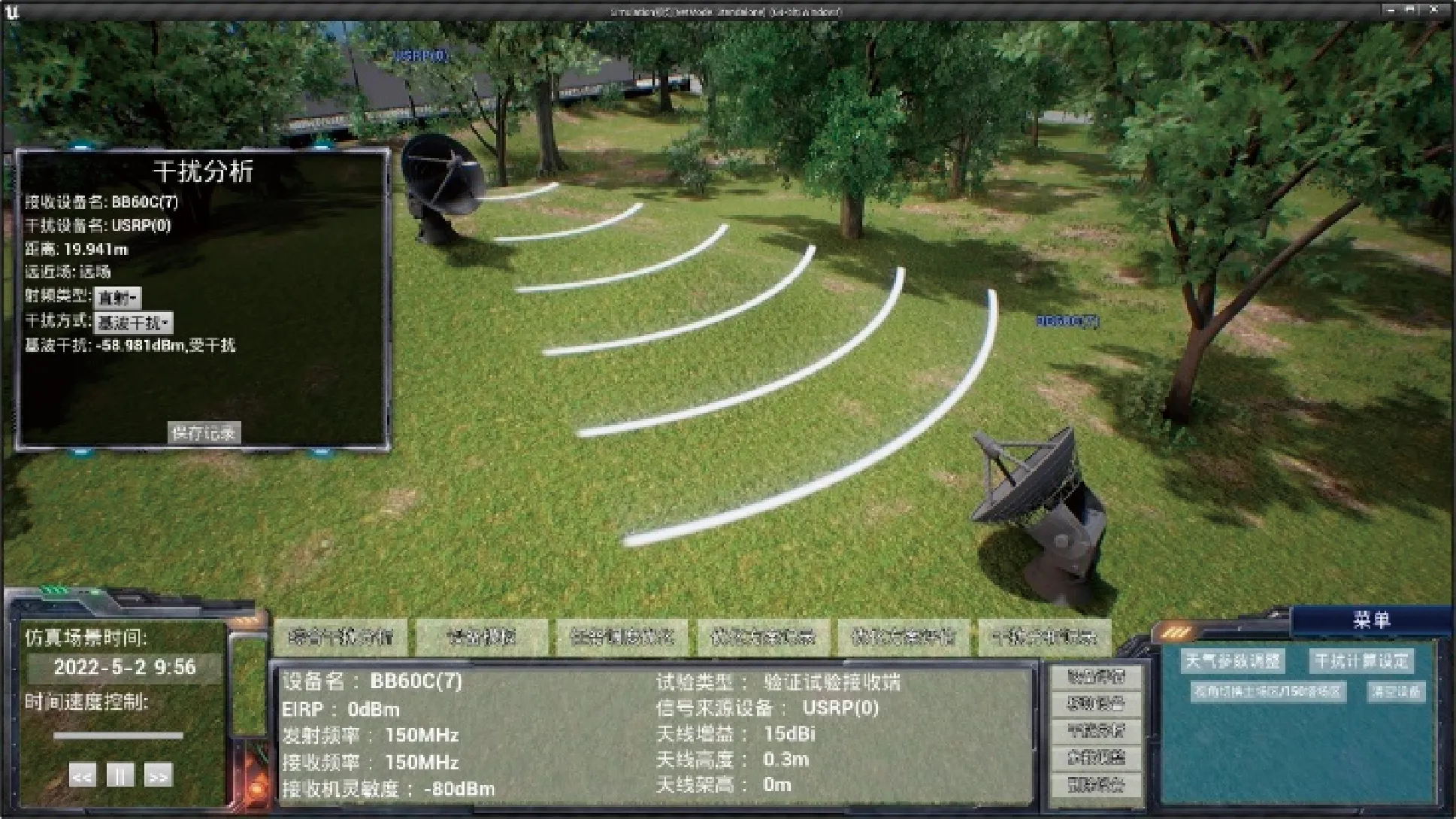
圖7 20 m仿真場景Fig.7 20 m simulation scene diagram

系統在模擬實際場景中,在參數設置上無法做到與實際環境完全一致。圖7中的仿真距離為19.941 m,與20 m相差不大。然而,當設備相距較遠時,UE4系統在計算二者之間的距離時就會出現較大的偏差。

表7為20 m距離的實際場景測量與系統仿真測試的基波干擾余量結果對比。

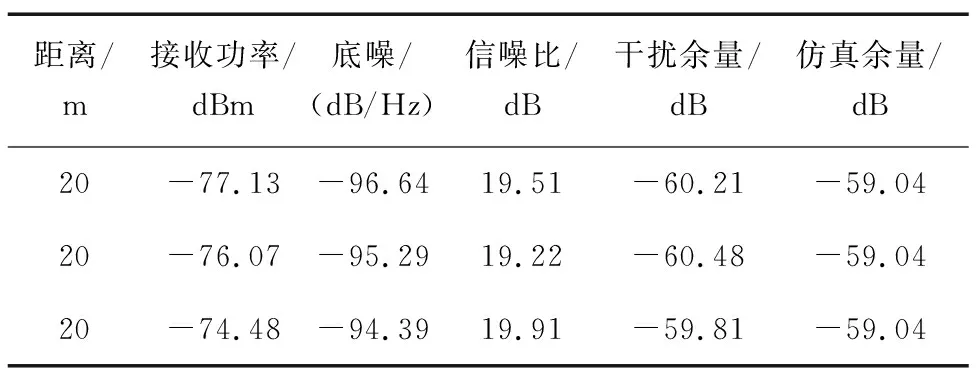
表7 小型天線20 m距離測試Tab.7 20 m distance test of small antenna

可以看出,在20 m的距離下,信噪比減小了12 dB左右,其干擾余量與系統仿真計算的干擾余量最大誤差為1.44 dB,不超過3 dB。3次測量的均值為60.17 dB,與仿真值相差1.13 dB。

此外,還進行了多種類型的干擾余量仿真計算,分別為基波干擾、基波亂真干擾、諧波干擾和諧波亂真干擾。仿真系統在10～60 m距離下的4種干擾余量計算結果如表8所示。

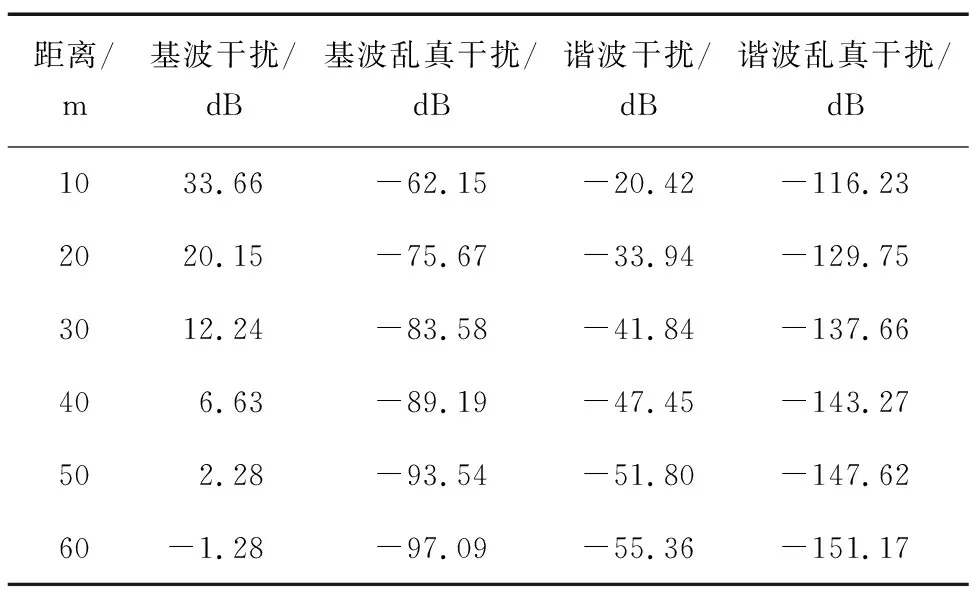
表8 小型天線多類型干擾仿真Tab.8 Multi-type interference simulation of small antenna

從表8可以看出,接收靈敏度為-80 dBm的情況下,4種干擾類型中,最主要且最嚴重的干擾是基波干擾。在50 m范圍內,基波干擾余量大于0,這意味著50 m內會受到基波干擾。其他3種干擾余量均小于0,其中諧波干擾余量相比另外2種又大很多,可以看出除了基波干擾,其次是諧波干擾影響較大。

基波干擾余量如圖8所示。可以看出,隨著距離的增加,干擾余量呈非線性趨勢不斷減小,在57 m左右干擾余量降為0。

綜上,根據實際環境測量與系統仿真測試對比,可以得出,仿真系統在UE4平臺中具有一定的有效性和準確性。

5 結束語

研究了基于UE4平臺的大型電子綜合試驗場的干擾分析方法。通過構建設備發射機模型和接收機模型,采用FDTD法、射線跟蹤法等方法,分析了場內不同類型的設備試驗、可能設備間的干擾余量,并考慮基波干擾、基波亂真干擾、諧波干擾和諧波亂真干擾4種干擾類型,分析了場區內存在的干擾類型,為試驗場區的頻譜優化和資源調度提供了數據支撐。