基于SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)航空壁板裝夾變形預(yù)測(cè)研究
劉紅軍,邵泓斌
(沈陽航空航天大學(xué)機(jī)電工程學(xué)院,遼寧沈陽 110136)
0 前言
薄壁件因其質(zhì)量輕、強(qiáng)度高、承載能力強(qiáng)等優(yōu)點(diǎn),如今被廣泛應(yīng)用于航空領(lǐng)域,如整體隔框、整體翼肋等[1]。現(xiàn)對(duì)機(jī)翼進(jìn)行盲制孔,因受其工裝夾具的影響,機(jī)翼中的壁板在安裝夾具后會(huì)相較于未安裝夾具前發(fā)生輕微變形,若不考慮則會(huì)導(dǎo)致最終盲制孔位置與期望的位置發(fā)生偏差,從而影響制孔精度。
受加工效率及加工條件的影響,對(duì)壁板變形量的測(cè)量無法通過眾多的激光測(cè)距傳感器實(shí)現(xiàn)。為提高盲制孔的加工精度,有必要建立一種航空壁板的變形預(yù)測(cè)算法,對(duì)航空壁板安裝夾具后的變形進(jìn)行準(zhǔn)確的預(yù)測(cè)。
趙欣等人[2]運(yùn)用Abaqus軟件模擬了葉片加工過程的變形量,并通過正交試驗(yàn)獲取切削參數(shù)、刀具傾角等數(shù)據(jù)來觀察葉片變形的影響規(guī)律,最后通過線性回歸的分析方法擬合出預(yù)測(cè)模型。王駿騰等[3]考慮到薄壁件的結(jié)構(gòu)復(fù)雜,且時(shí)變加工工況造成的殘余應(yīng)力難以獲取,分析了幾種典型裝夾方式的感知過程,提出了一種感知預(yù)測(cè)模型,實(shí)驗(yàn)結(jié)果表明:預(yù)測(cè)值與實(shí)測(cè)值相比,誤差為13%,具有較好的一致性。CHENG等[4]采用有限元仿真的方法建立了三維鈦合金薄壁銑削模型,并分析了其變形規(guī)律。于金、王胤棋[5]為解決Abaqus軟件仿真運(yùn)算時(shí)間較長的問題,采用Python語言編寫腳本對(duì)Abaqus軟件進(jìn)行了二次開發(fā),仿真預(yù)測(cè)時(shí)間縮短,可較好地預(yù)測(cè)大型曲面薄壁件加工時(shí)的變形情況。王慶霞等[6]運(yùn)用AdvantEdge軟件建立三維銑削加工的有限元模型,根據(jù)仿真得到的結(jié)果確立了進(jìn)給速度、切削力和工件切削時(shí)加工變形之間的多項(xiàng)式數(shù)值模型,從而實(shí)現(xiàn)對(duì)加工過程中變形的實(shí)時(shí)預(yù)測(cè)。屈力剛等[7]首先根據(jù)薄壁件的加工路徑構(gòu)建了UKF預(yù)測(cè)模型,其次把在機(jī)測(cè)量系統(tǒng)的檢測(cè)數(shù)據(jù)作為已知噪聲輸入到UKF算法中進(jìn)行預(yù)測(cè)模型的訓(xùn)練,最后使用MATLAB預(yù)測(cè)出零件的變形量,根據(jù)試驗(yàn)對(duì)比,預(yù)測(cè)變形量精度從45.7%提高至74.2%。HUANG等[8]為了提升預(yù)測(cè)零件變形的計(jì)算效率,首次使用了結(jié)構(gòu)分析、特殊網(wǎng)格生成和結(jié)構(gòu)靜態(tài)剛度修正結(jié)合的方法,提出一種新的有限元模型,最后計(jì)算零件隨時(shí)間和位置變化的變形量,預(yù)測(cè)壁厚誤差。秦國華等[9]針對(duì)航空薄壁零件,采用了神經(jīng)網(wǎng)絡(luò)的方法對(duì)裝夾布局進(jìn)行了預(yù)測(cè)、控制與優(yōu)化。韓軍等人[10]將Abaqus有限元仿真與BP神經(jīng)網(wǎng)絡(luò)結(jié)合的方法應(yīng)用到齒圈裝夾變形預(yù)測(cè)中,得到的預(yù)測(cè)結(jié)果與實(shí)際值相比較誤差在0.05%之內(nèi)。陳永當(dāng)?shù)萚11]首先運(yùn)用Python對(duì)Abaqus進(jìn)行二次開發(fā),對(duì)建模周期進(jìn)行了縮短和簡化,其次通過對(duì)BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練,對(duì)最大鉚接變形量進(jìn)行了預(yù)測(cè),性能較好。
上述學(xué)者對(duì)模型的變形預(yù)測(cè)大多使用Abaqus有限元軟件進(jìn)行分析,缺點(diǎn)是預(yù)測(cè)時(shí)間較長,效率低。韓軍等人[10]通過Abaqus與BP神經(jīng)網(wǎng)絡(luò)結(jié)合的方法,先通過Abaqus仿真模型獲取訓(xùn)練樣本的數(shù)據(jù),再使用BP神經(jīng)網(wǎng)絡(luò)的方法進(jìn)行變形預(yù)測(cè),大大減少了運(yùn)算時(shí)間,提高了預(yù)測(cè)的效率,但BP神經(jīng)網(wǎng)絡(luò)并沒有對(duì)初始權(quán)值和閾值進(jìn)行優(yōu)化,容易陷入局部最優(yōu)解,造成預(yù)測(cè)值的精準(zhǔn)度降低。李樂等人[12]使用粒子群算法對(duì)BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值與閾值進(jìn)行了初次優(yōu)化,預(yù)測(cè)精度有了較大的提升。
本文作者將根據(jù)航空壁板實(shí)際的裝夾情況,采用Abaqus有限元仿真與神經(jīng)網(wǎng)絡(luò)相結(jié)合的方法,首先對(duì)航空壁板進(jìn)行有限元分析,從而獲取神經(jīng)網(wǎng)絡(luò)所需要的訓(xùn)練以及預(yù)測(cè)數(shù)據(jù);其次提出一種改進(jìn)的神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法,即SSA-PSO-BP預(yù)測(cè)算法,快速且準(zhǔn)確地預(yù)測(cè)航空壁板裝夾后的變形量。
1 航空壁板裝夾變形有限元分析
對(duì)現(xiàn)場安裝夾具后3個(gè)激光測(cè)距傳感器的測(cè)距值進(jìn)行記錄,作為神經(jīng)網(wǎng)絡(luò)的輸入值輸入到Abaqus軟件中,對(duì)壁板進(jìn)行仿真變形預(yù)測(cè),將得到的8個(gè)預(yù)測(cè)值作為神經(jīng)網(wǎng)絡(luò)的輸出值。總共得出50組數(shù)據(jù)集作為神經(jīng)網(wǎng)絡(luò)的訓(xùn)練以及預(yù)測(cè)。
此次使用Abaqus2020有限元軟件建立壁板裝夾變形的仿真分析,研究壁板制孔處x方向的位移,主要涉及幾何模型建立、材料屬性賦予、邊界條件及接觸定義、網(wǎng)格劃分共4部分內(nèi)容。
(1)幾何模型設(shè)計(jì)與建立。對(duì)航空壁板實(shí)際模型進(jìn)行適當(dāng)?shù)暮喕⒃赟olidWorks軟件中進(jìn)行等比例建模,最終導(dǎo)入Abaqus軟件中進(jìn)行有限元分析。
(2)材料屬性賦予。航空壁板的材料為Ti-6Al-4V,其中彈性模量E=110 GPa,密度ρ=4 510 kg/m3,泊松比μ=0.34。因航空壁板在實(shí)際裝夾過程中的塑性屈服并不明顯,此處采用Johnson-Cook模型[13]來描述Ti-6Al-4V鈦合金的本構(gòu)關(guān)系,表達(dá)式如式(1)所示:
(1)
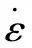
(3)邊界條件及接觸定義。根據(jù)現(xiàn)場實(shí)際裝夾情況,壁板的上下兩段與飛機(jī)翼框接觸且固定約束,僅允許在x軸與y軸方向上移動(dòng)。
(4)網(wǎng)格劃分。為壁板劃分網(wǎng)格時(shí),考慮到其形狀復(fù)雜且不規(guī)則,將其合理地劃分為四面體結(jié)構(gòu)網(wǎng)格,選擇常用于接觸分析的三維應(yīng)力線性單元,單元類型為C3D10。
仿真后的位移變化云圖如圖1所示,最大變形量約為2.776 mm。以同樣的方法將測(cè)得的不同激光傳感器數(shù)值進(jìn)行模擬仿真,總共得到50組數(shù)據(jù)作為神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練樣本和預(yù)測(cè)樣本。50組數(shù)據(jù)如表1所示。
2 SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)模型
2.1 BP神經(jīng)網(wǎng)絡(luò)
人工神經(jīng)網(wǎng)絡(luò)(Artificial Neural Networks,ANN)是1980年以來人工智能領(lǐng)域的重點(diǎn)研究內(nèi)容,主要用于處理多節(jié)點(diǎn)和多輸出點(diǎn)的網(wǎng)絡(luò)結(jié)構(gòu)[14]。BP神經(jīng)網(wǎng)絡(luò)屬于人工神經(jīng)網(wǎng)絡(luò)的一種,屬于多層前饋神經(jīng)網(wǎng)絡(luò),其拓補(bǔ)結(jié)構(gòu)主要由輸入層、隱含層、輸出層組成。
BP神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)如圖2所示。

圖2 BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
目前,BP神經(jīng)網(wǎng)絡(luò)已經(jīng)足夠成熟,可以解決大部分的預(yù)測(cè)問題,但是在使用過程中也逐漸發(fā)現(xiàn)其有一定的缺陷:即每次賦予的權(quán)值與閾值都是隨機(jī)的,造成整體神經(jīng)網(wǎng)絡(luò)的收斂速度過慢,并且容易陷入局部最優(yōu)解。
因此本文作者基于傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò),在其原有的基礎(chǔ)上先進(jìn)行一次PSO粒子群優(yōu)化算法的優(yōu)化,再進(jìn)行一次SSA麻雀搜索算法的優(yōu)化。其目的是為了對(duì)BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值與閾值進(jìn)行兩次尋優(yōu),從而得到改進(jìn)的BP神經(jīng)網(wǎng)絡(luò),即SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)算法,其流程如圖3所示。
圖3 SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)算法流程
2.2 SSA原理
麻雀搜索算法(Sparrow Search Algorithm,SSA)是由薛建凱[15]通過模擬麻雀在自然界的生存過程提出的一種群體優(yōu)化算法,相較于之前的蝙蝠算法、灰狼優(yōu)化算法、鯨魚優(yōu)化算法等,SSA具有精度更高、收斂速度更快、穩(wěn)定性更強(qiáng)的優(yōu)點(diǎn),并且具有較好的全局尋優(yōu)能力。
為了更好地生存,麻雀種群通常分為兩種類型:發(fā)現(xiàn)者和加入者,發(fā)現(xiàn)者負(fù)責(zé)尋找食物,為整個(gè)種群提供覓食的方向,其生存能力較強(qiáng),加入者通過發(fā)現(xiàn)者來獲取食物,屬于弱勢(shì)個(gè)體。發(fā)現(xiàn)者與加入者的身份是可以動(dòng)態(tài)變化的,只要能找到食物,每只麻雀都可以成為發(fā)現(xiàn)者,但是發(fā)現(xiàn)者與加入者占整個(gè)種群的比例是不變的,即一只麻雀成為發(fā)現(xiàn)者必有另一只麻雀成為加入者。此外,當(dāng)麻雀意識(shí)到危險(xiǎn)時(shí),為了保證安全,群體邊緣的麻雀會(huì)迅速向安全區(qū)域移動(dòng),不斷更新自己的位置。
(1)發(fā)現(xiàn)者的位置更新如式(2)所示:
(2)
式中:t為當(dāng)前的迭代次數(shù),j=1,2,3,…,d;M表示最大的迭代次數(shù);Xi,j表示第i個(gè)麻雀在第j維中的位置信息;α是(0,1)內(nèi)的隨機(jī)數(shù);R2表示預(yù)警值,Ts表示安全值,其中R2∈[0,1],Ts∈[0.5,1];Q為服從正態(tài)分布的隨機(jī)數(shù);L代表一個(gè)大小為1×d維的矩陣,且矩陣中的各個(gè)元素都為1。
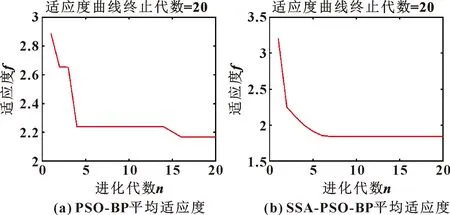
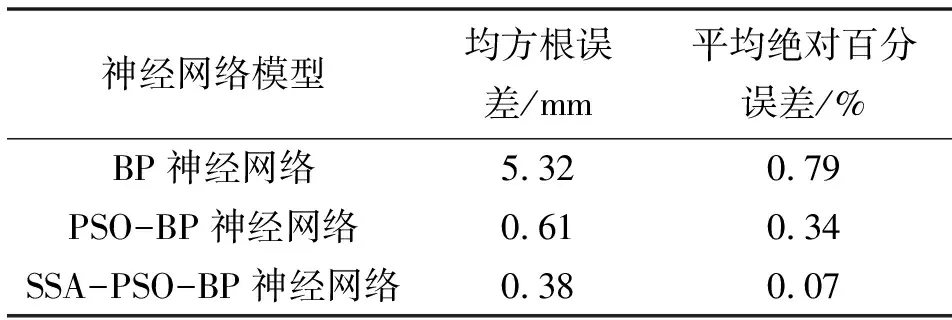
當(dāng)R2 (2)加入者的位置更新如式(3)所示: (3) 式中:Xp表示當(dāng)前種群內(nèi)的最優(yōu)位置;Xworst表示當(dāng)前種群內(nèi)的最差位置;A表示一個(gè)大小為1×d維的矩陣,矩陣中的每個(gè)元素被隨機(jī)賦值為1或-1,且滿足A+=AT(AAT)-1。 當(dāng)i>n/2時(shí),表示種群當(dāng)中的第i個(gè)加入者沒有找到食物,適應(yīng)度值較低,需要前往其他區(qū)域?qū)ふ沂澄铮垣@取更多的食物補(bǔ)充能量。 (3)在進(jìn)行種群模型構(gòu)建的過程中,假定種群中有10%~20%的麻雀會(huì)提前預(yù)知到風(fēng)險(xiǎn),在向種群發(fā)出預(yù)警信號(hào)后麻雀會(huì)迅速做出反捕食行為,其位置更新公式如式(4)所示: (4) 式中:Xbest是當(dāng)前種群內(nèi)的最優(yōu)位置;β表示系統(tǒng)步長控制參數(shù),其數(shù)值滿足均值為0、方差為1,并且服從正態(tài)分布;K為[-1,1]內(nèi)的隨機(jī)數(shù);fi為當(dāng)前第i個(gè)麻雀的適應(yīng)度值;fg表示當(dāng)前全局最佳的適應(yīng)度值;fw表示當(dāng)前全局最差的適應(yīng)度值;ε表示最小的常數(shù),作用是為了避免分母為零的情況出現(xiàn)。 當(dāng)fi>fg時(shí),表示此時(shí)麻雀處于邊緣位置,極易被捕食者發(fā)現(xiàn)并受到攻擊;當(dāng)fi=fg時(shí),表示此時(shí)處于種群中心的麻雀意識(shí)到了危險(xiǎn),需要立即更新自身的位置向危險(xiǎn)區(qū)域的麻雀靠攏。 根據(jù)算法流程圖可知,對(duì)BP神經(jīng)網(wǎng)絡(luò)權(quán)值與閾值進(jìn)行PSO算法的初次優(yōu)化,其中PSO算法的具體參數(shù)設(shè)置為迭代次數(shù)為20,種群規(guī)模為10,學(xué)習(xí)因子c1=c2=1.494 45;其次采用迭代速度快、全局尋優(yōu)能力強(qiáng)的SSA對(duì)權(quán)值與閾值進(jìn)行二次尋優(yōu),SSA的參數(shù)為迭代次數(shù)為20,種群規(guī)模為10,發(fā)現(xiàn)者和加入者各占種群數(shù)目的20%,預(yù)警值R2=0.8。 根據(jù)上述參數(shù)設(shè)定,選取有限元仿真數(shù)據(jù)中45組數(shù)據(jù)作為SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練數(shù)據(jù)集對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練,剩余5組數(shù)據(jù)作為神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)數(shù)據(jù)集,驗(yàn)證神經(jīng)網(wǎng)絡(luò)是否符合要求。 為驗(yàn)證此次建立的SSA-PSO-BP網(wǎng)絡(luò)與BP神經(jīng)網(wǎng)絡(luò)以及PSO-BP兩種神經(jīng)網(wǎng)絡(luò)的不同之處,用訓(xùn)練集對(duì)BP網(wǎng)絡(luò)、PSO-BP網(wǎng)絡(luò)以及SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練后,分別用于對(duì)航空壁板變形進(jìn)行預(yù)測(cè)。期望值與各個(gè)神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)值的對(duì)比如圖4所示,各個(gè)神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)誤差如圖5所示。 圖4 預(yù)測(cè)值與期望值對(duì)比 圖5 誤差對(duì)比 根據(jù)圖4與圖5可以看出:除4號(hào)樣本SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)值誤差較大,其他4組測(cè)試樣本的SSA-PSO-BP預(yù)測(cè)值較BP與PSO-BP兩種神經(jīng)網(wǎng)絡(luò),其預(yù)測(cè)的準(zhǔn)確性明顯優(yōu)于后兩者,與期望值的擬合效果更佳。 圖6為兩種神經(jīng)網(wǎng)絡(luò)的適應(yīng)度進(jìn)化曲線,與PSO-BP神經(jīng)網(wǎng)絡(luò)相比,SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)在相同20次迭代次數(shù)下適應(yīng)度趨于平穩(wěn)的速率更快,經(jīng)過7次迭代便達(dá)到了適應(yīng)度的全局最優(yōu)值,并且適應(yīng)度較PSO-BP神經(jīng)網(wǎng)絡(luò)也有了明顯的降低。因此,文中所提出的SSA-PSO-BP優(yōu)化算法對(duì)BP神經(jīng)網(wǎng)絡(luò)的收斂速度及預(yù)測(cè)精度提升較大。 圖6 適應(yīng)度曲線對(duì)比 為評(píng)價(jià)各神經(jīng)網(wǎng)絡(luò)模型的性能,采用均方根誤差(RMSE)以及平均絕對(duì)百分誤差(MAPE)對(duì)預(yù)測(cè)結(jié)果進(jìn)行精度評(píng)定。RMSE可以比較預(yù)測(cè)值與真實(shí)值之間的偏差,MAPE可以衡量一個(gè)模型預(yù)測(cè)結(jié)果的準(zhǔn)確性。相應(yīng)的計(jì)算公式如式(5)(6)所示: (5) (6) 對(duì)預(yù)測(cè)結(jié)果進(jìn)行精度評(píng)定,結(jié)果如表2所示。 表2 模型準(zhǔn)確度對(duì)比 由表2可知:BP神經(jīng)網(wǎng)絡(luò)的均方根誤差是5.32 mm,平均絕對(duì)百分誤差為0.79%;PSO-BP神經(jīng)網(wǎng)絡(luò)的均方根誤差是0.61 mm,平均絕對(duì)百分誤差為0.34%,比BP神經(jīng)網(wǎng)絡(luò)有了明顯的降低;而SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)均方根誤差是0.38 mm,平均絕對(duì)百分誤差為0.07%,相較于BP與PSO-BP神經(jīng)網(wǎng)絡(luò)模型精度有了進(jìn)一步的提升,說明SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)具有較好的全局精度。 為解決航空壁板裝夾變形預(yù)測(cè)問題,提出了一種Abaqus仿真與神經(jīng)網(wǎng)絡(luò)算法相結(jié)合的方式,并對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行了優(yōu)化,實(shí)驗(yàn)結(jié)果表明,相較于傳統(tǒng)的有限元模擬仿真,以及傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò),此次運(yùn)用Abaqus與SSA-PSO-BP神經(jīng)網(wǎng)絡(luò)結(jié)合的這一結(jié)合思維,首先通過有限元仿真獲取神經(jīng)網(wǎng)絡(luò)所需要的訓(xùn)練以及預(yù)測(cè)數(shù)據(jù),其次通過對(duì)BP神經(jīng)網(wǎng)絡(luò)算法加以改進(jìn)將其權(quán)值與閾值進(jìn)行二次優(yōu)化,最終表明構(gòu)建的壁板裝夾變形預(yù)測(cè)數(shù)字化模型具有很高的精度和很快的收斂速度,并且極大地減少了運(yùn)算時(shí)間,提高了預(yù)測(cè)的效率。3 神經(jīng)網(wǎng)絡(luò)實(shí)例應(yīng)用
3.1 神經(jīng)網(wǎng)絡(luò)參數(shù)設(shè)定
3.2 三種神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)值對(duì)比
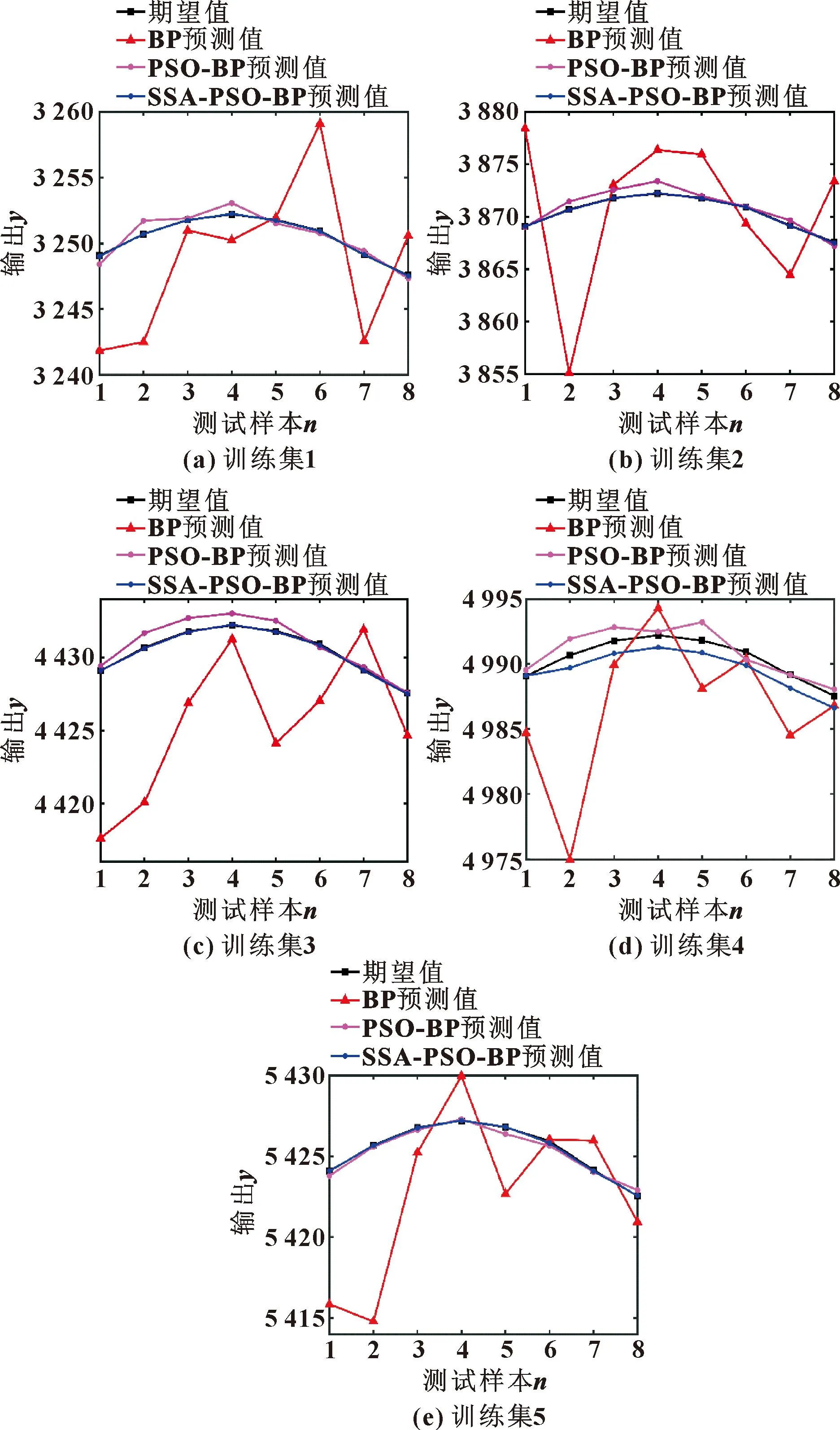
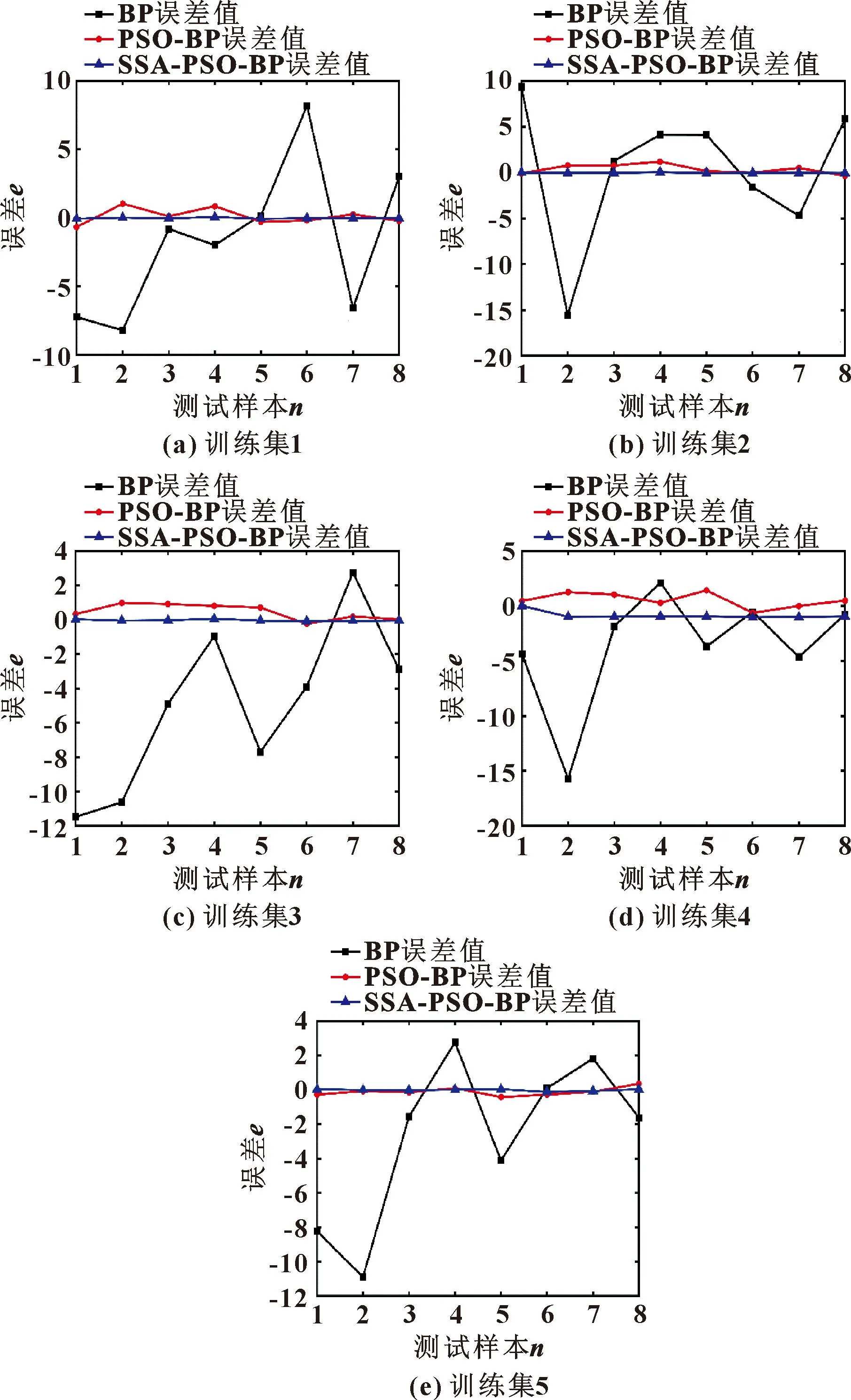
4 結(jié)論

