新型變指數趨近律的PMSM滑模控制
李璐,譚草,2,張玉學,郭春霖,孫兆岳,王子喆
(1.山東理工大學交通與車輛工程學院,山東淄博 255049;2.山東中保康醫療器具有限公司,山東淄博 256407)
0 前言
近年來,電力電子技術快速發展。永磁同步電機(Permanent Magnet Synchronous Motor,PMSM)具有體積小、質量輕、功率密度高、啟動轉矩大等優點[1-3],已在汽車、航天、機器人等領域得到了廣泛的應用。
滑模控制作為一種變結構非線性的控制方法,相比于傳統的PI控制具有響應快速和強魯棒性的優點,并且對內部參數和外部擾動不敏感,廣泛應用于PMSM調速系統。但滑模控制的一個主要缺點是系統狀態變量在滑模面附近做滑模運動時,會發生抖振現象[4-6]。解決抖振問題已成為滑模控制的熱點研究問題。
文獻[7]提出一種基于新型滑模趨近律的魯棒控制策略,并在位置環引入了積分-非奇異終端滑模控制器,仿真驗證了該控制器可有效克服系統結構參數的變化,并提高了響應能力。文獻[8]提出一種新型分數階趨近律,將冪次趨近律與分數階微積分相結合,應用分段型指數函數代替趨近律中的符號函數;仿真結果表明:該方法能有效解決傳統滑模控制中存在的問題,具有抖振小、控制精度高等優點。文獻[9]提出一種基于高階滑模觀測器與新型滑模速度控制器相結合的PMSM無傳感器矢量控制方法,用高階滑模觀測器代替傳統滑模觀測器,用新型滑模轉速控制器代替傳統比例積分轉速控制器,仿真結果表明:新型雙滑模控制系統轉速的超調量與抖振更小。文獻[10]采用邊界層可變的正弦型飽和函數替代傳統符號函數,提出一種用于PMSM無傳感器控制的軟開關滑模觀測器,實驗結果表明,新型滑模控制器有效消除了估計結果的抖振。
本文作者在傳統冪次趨近律的基礎上引入一個變指數項,加快了系統的收斂速度,并且將滑模趨近律的符號函數替換成正弦飽和函數,抑制了系統的抖振問題;針對外部擾動對滑模控制系統的影響,設計非奇異快速終端滑模擾動觀測器,避免較大的滑模增益,解決系統的抖振問題。仿真實驗結果表明:結合擾動觀測器的新型變指數趨近律滑模控制系統具有響應速度快、抖振小、抗干擾能力強的特點。
1 PMSM數學建模
永磁同步電機是一個非線性、多變量、強耦合的復雜系統。忽略永磁同步電機鐵芯飽和、磁滯損耗、渦流損耗等影響,對永磁同步電機三相坐標系進行數學建模,永磁同步電機同步旋轉坐標系下的數學模型[11]為
(1)
(2)
(3)
對于表貼式PMSM,由于轉子磁路對稱,有Ld=Lq,故式(3)可以表示為
Te=3/2npφmiq
(4)
電機機械運動方程:
(5)
一般在電機調速系統中,把外界負載TL看作外部擾動d(t),則式(5)可表示為
(6)
其中:Rs為定子電阻;ωe為轉子電角速度;id、iq分別為定子d、q軸電流;ud、uq分別為定子d、q軸電壓;Ld、Lq分別為定子d、q軸電感;np為電機極對數;φm為永磁體磁鏈;w為微分算子;Te、TL分別為電磁轉矩和負載轉矩;J為轉動慣量;B為黏滯摩擦系數;d(t)為外部擾動。
2 控制器的設計及穩定性證明
2.1 改進變指數趨近律滑模控制器
首先定義電機的參考轉速為ωref,實際轉速為ωm,可得出速度誤差和其變化率:
(7)
非奇異終端滑模(Non-singular Terminal Sliding Mode,NTSM)解決了終端滑模奇異性問題,但在系統誤差到達滑模面后,其收斂速度表現的要比線性函數構成的滑模面慢。因此,構建非奇異快速終端滑模控制器(Non-singular Fast Terminal Sliding Mode-Controller,NFTSMC)的表達式[12]為
(8)
其中:S(x)是滑模面;x是系統狀態變量;θ>0;p、q均為大于0的奇數,且q
令S=0,得到速度誤差變化率為
(9)
由式(9)可知,系統誤差做趨近滑模面的運動時,誤差收斂速度取決于指數項,當系統誤差接近平衡點時,誤差收斂速度主要取決于線性項,保證了全局的收斂速度。
基于傳統冪次趨近律的基礎建立了快速冪次趨近律,這種新型的趨近律保持了傳統冪次趨近律的優點,又進一步加速了全局收斂速度,抑制了系統抖振。現給出其具體的形式,如下所示:
(10)
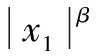
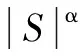
為進一步抑制系統的抖振問題,繼續對上述趨近律進行改進,采用一種正弦飽和函數代替符號函數。飽和函數法又稱邊界層法,利用邊界層原理使系統變成連續系統,新型正弦飽和函數的表達式[13]為
(11)
其中:Δ為邊界層的厚度,λ=π/2Δ。這樣,在飽和層外采用開關切換控制,飽和層內采用線性控制,既保證了收斂速度,又減小了高頻切換產生的抖振,保證電機在中低速場合的跟蹤性能。
則結合式(6)(8)(10),新型非奇異快速終端滑模控制律如下:
(12)
2.2 速度控制器穩定性證明
利用Lyapuov穩定性條件加以說明。現定義一個存在一階偏導數的Lyapuov函數V(x),如下:
V(x)=1/2S2
(13)
求導得到:
(14)
由式(8)可知:
(15)
上文已推出iq表達式:
(16)
則有:
(17)
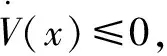
3 擾動觀測器的設計及穩定性證明
針對滑模變結構控制在負載擾動時動態性能不佳的問題,設計非奇異快速終端滑模轉矩觀測器,實時觀測負載轉矩的變化,并將觀測得到的擾動量前饋至電流給定,克服了負載擾動對系統控制性能的影響。
在一個控制周期內,負載轉矩變化較慢[14],一階導數可看成0,有
(18)
即
(19)
以電機機械角速度ωm和負載擾動量d(t)構建狀態方程[12]:
(20)
將機械角速度和系統負載擾動作為觀測對象,構建非奇異快速終端滑模觀測器方程為
(21)
其中:g為觀測器增益;f(eω)為觀測的滑模控制率。兩次相減得出誤差方程為
(22)
其中:ed為擾動觀測誤差;eω為速度觀測誤差。
同樣選取非奇異快速終端滑模作為擾動觀測器滑模面:
(23)
結合上文的新型趨近律,得到擾動觀測器的趨近律為
C|Sω|αsat(Sω)+ε|eω|βSω-B/Jeω
(24)
由式(23)(25)可得
(25)
則有
ε|eω|βSω-B/Jeω)≤0
(26)
由式(26)可知,擾動觀測器符合李雅普諾夫第二穩定性理論。圖1為文中NFTSMC矢量控制策略系統控制框圖。
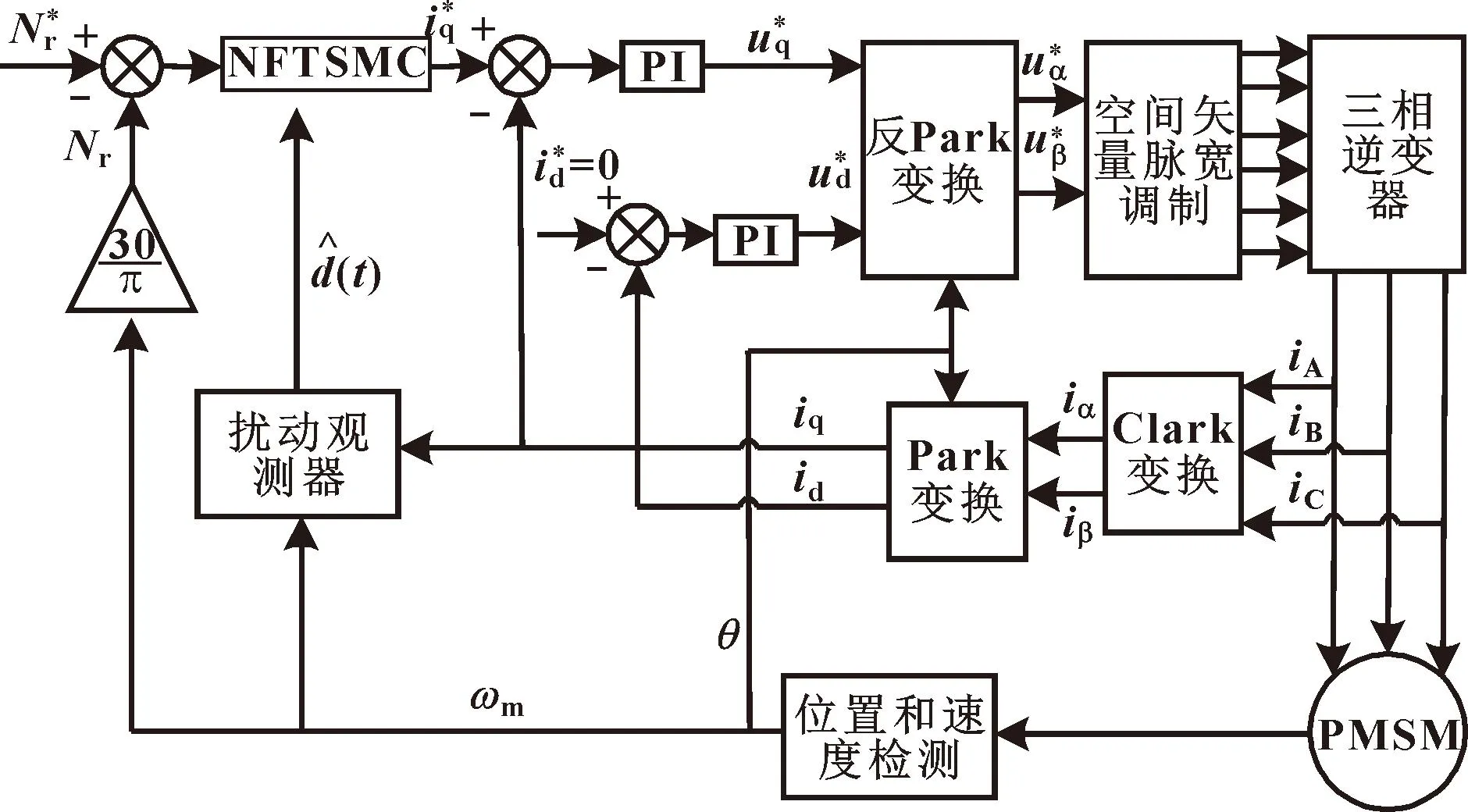
圖1 系統控制框圖
4 結果及分析
搭建的基于RTU-BOX的調速系統實驗平臺實物如圖2所示,實驗平臺包括直流電源、三相全橋逆變器、RTU-BOX控制器、實驗電機、負載電機、轉速轉矩傳感器。
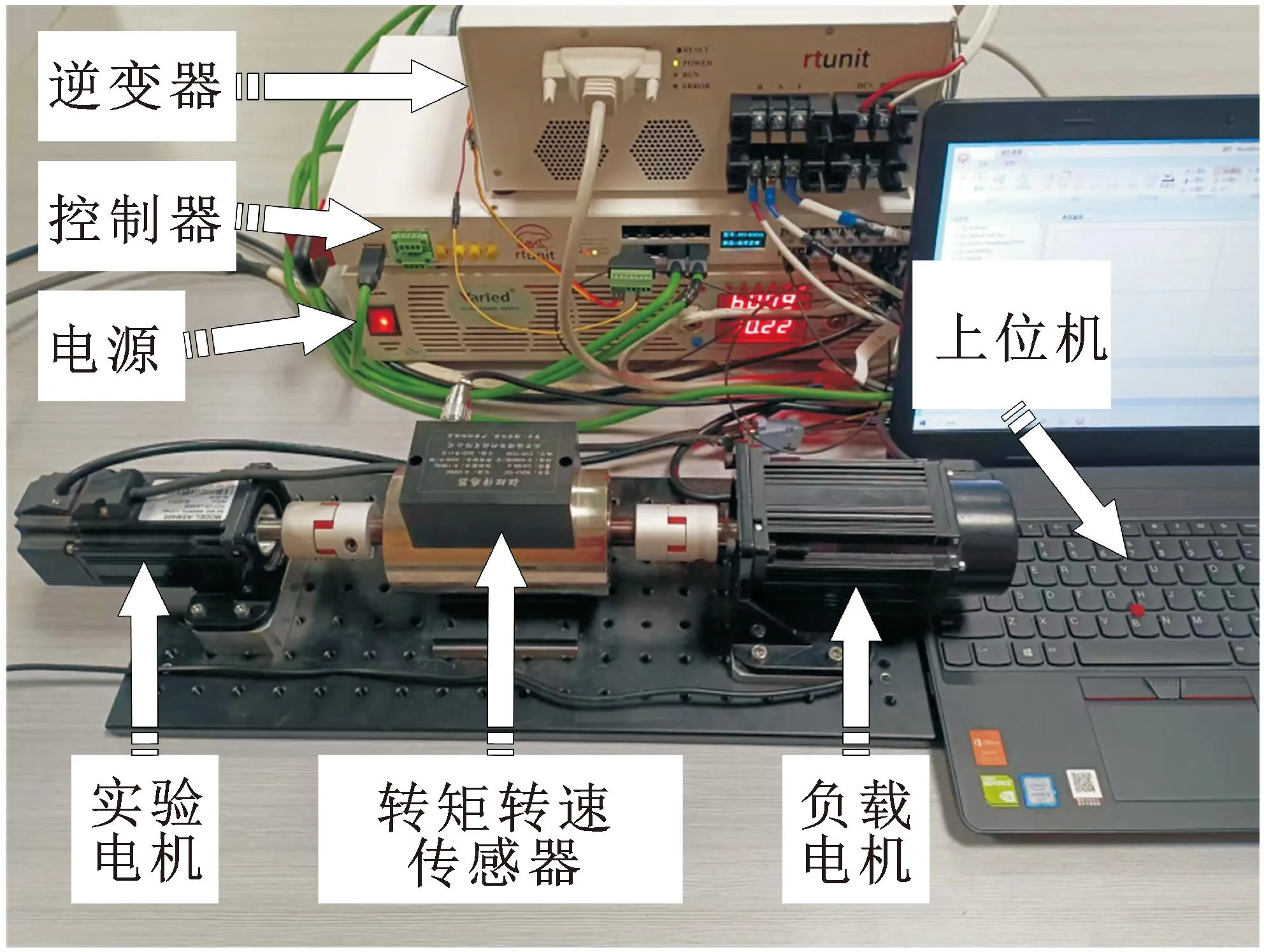
圖2 永磁同步電機實驗平臺
為驗證引入負載擾動觀測器的基于新型變指數趨近律的NFTSMC轉速控制策略控制效果,將MATLAB/Simulink調速系統NFTSMC矢量控制仿真模型嵌入控制器,在保證電機參數相同且采樣時間以及仿真條件均保持一致的條件下對基于飽和函數的變指數趨近律的非奇異快速終端滑模速度控制器進行仿真,同時與基于符號函數的變指數趨近律的非奇異終端滑模速度控制器進行性能對比。表1為電機參數。

表1 永磁同步電機的主要參數
4.1 啟動工況性能實驗
圖3為基于不同滑模控制策略控制下的電機啟動轉速實驗波形,電機給定參考轉速為600 r/min。其中NTSMC-sgn為基于符號函數的變指數趨近律非奇異終端滑模控制,NFTSMC-sat為基于飽和函數的變指數趨近律非奇異快速終端滑模控制,下文NFTSMC-sat+DOB為結合擾動觀測器的基于飽和函數的變指數趨近律非奇異快速終端滑模控制。
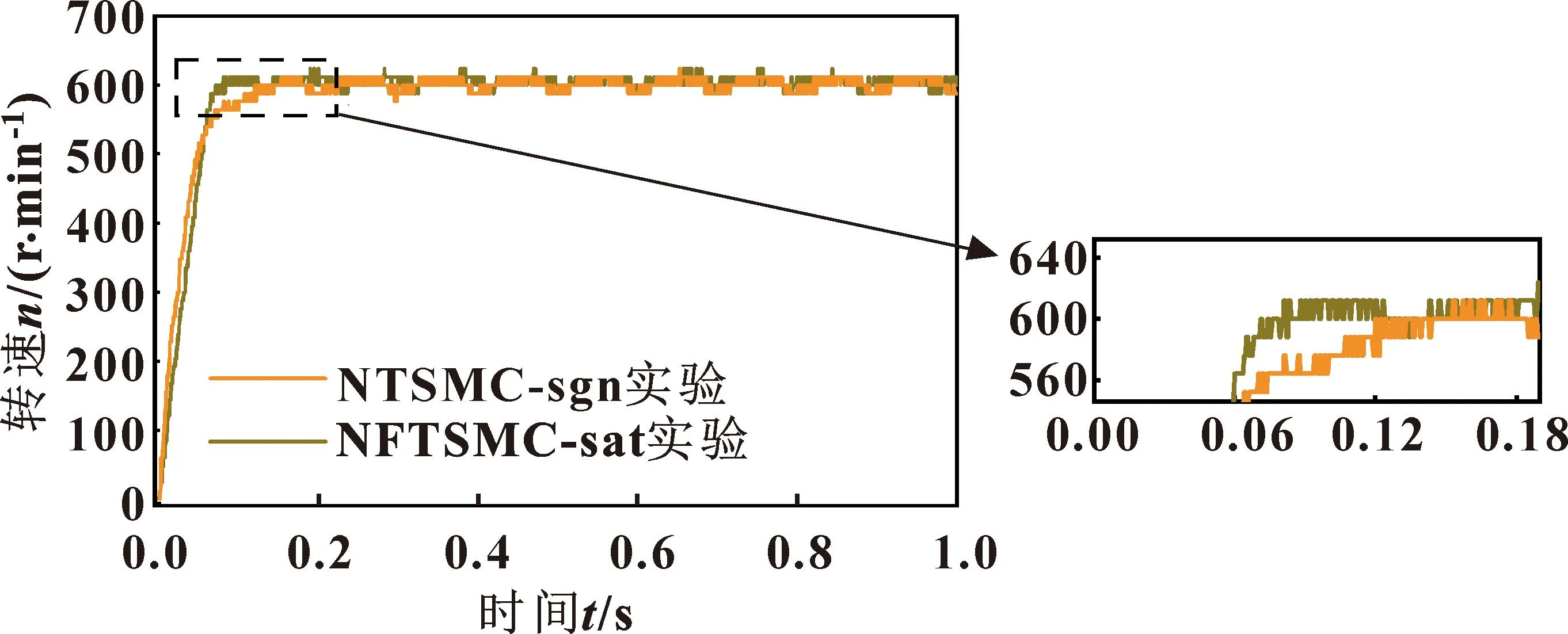
圖3 啟動工況永磁同步電機轉速
由圖3可知:基于符號函數的變指數趨近律非奇異終端滑模控制的電機在0.118 s達到參考轉速,而所設計的基于飽和函數的變指數趨近律非奇異快速終端滑模控制的電機在0.071 s就達到參考轉速,并且達到穩定前無超調。實驗證明了所設計控制器的合理性。
4.2 變負載工況性能仿真
啟動階段給定電機負載轉矩0 N·m,在0.2 s時突增負載,變成4 N·m,圖4為不同控制策略下電機轉速響應曲線。
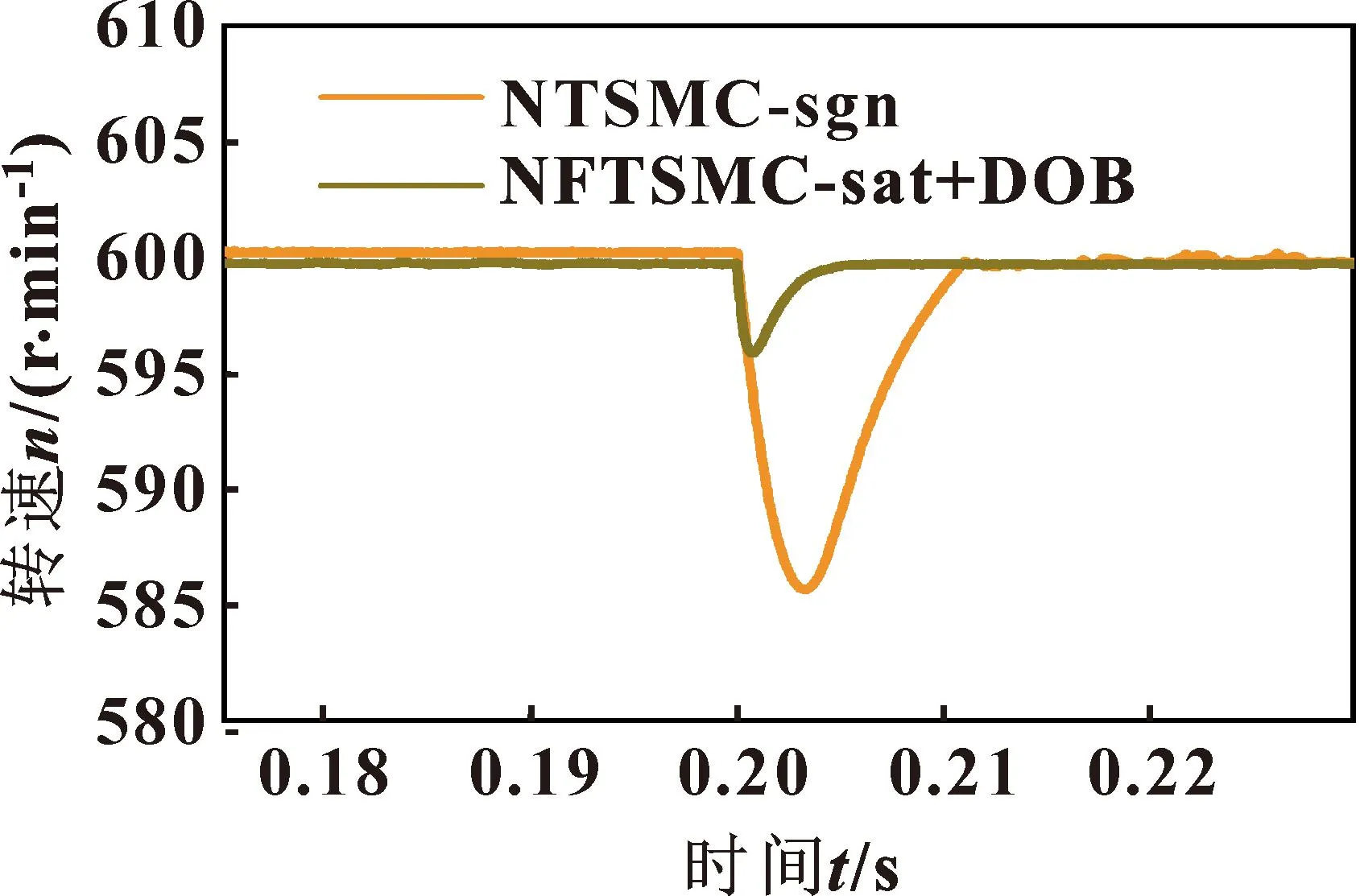
圖4 變負載工況永磁同步電機轉速
由圖4可知:基于符號函數的變指數趨近律非奇異終端滑模控制的電機轉速下降到585.6 r/min,且穩定時間較長,轉速穩定過程中抖振較大;結合擾動觀測器的基于飽和函數的變指數趨近律非奇異快速終端滑模控制的電機轉速下降到596.1 r/min,且可以很快穩定到參考轉速,穩定后轉速波動小。因此,采用基于飽和函數的新型變指數趨近律的滑模控制結合擾動觀測器可以有效抵抗外界負載干擾,恢復時間短,且有效降低抖振。
由圖5可知:在0.2 s突加4 N·m負載,兩種滑模控制下的電機皆很快達到參考轉矩,但基于符號函數的變指數趨近律非奇異終端滑模控制的電機轉矩達到穩定前超調量比較大;采用引入負載擾動觀測器的基于飽和函數的變指數趨近律非奇異快速終端滑模控制的電機轉矩在0.206 s就達到了穩定,并且僅略有超調,且穩定階段波形毛刺少,抖振小,電機轉矩平穩。
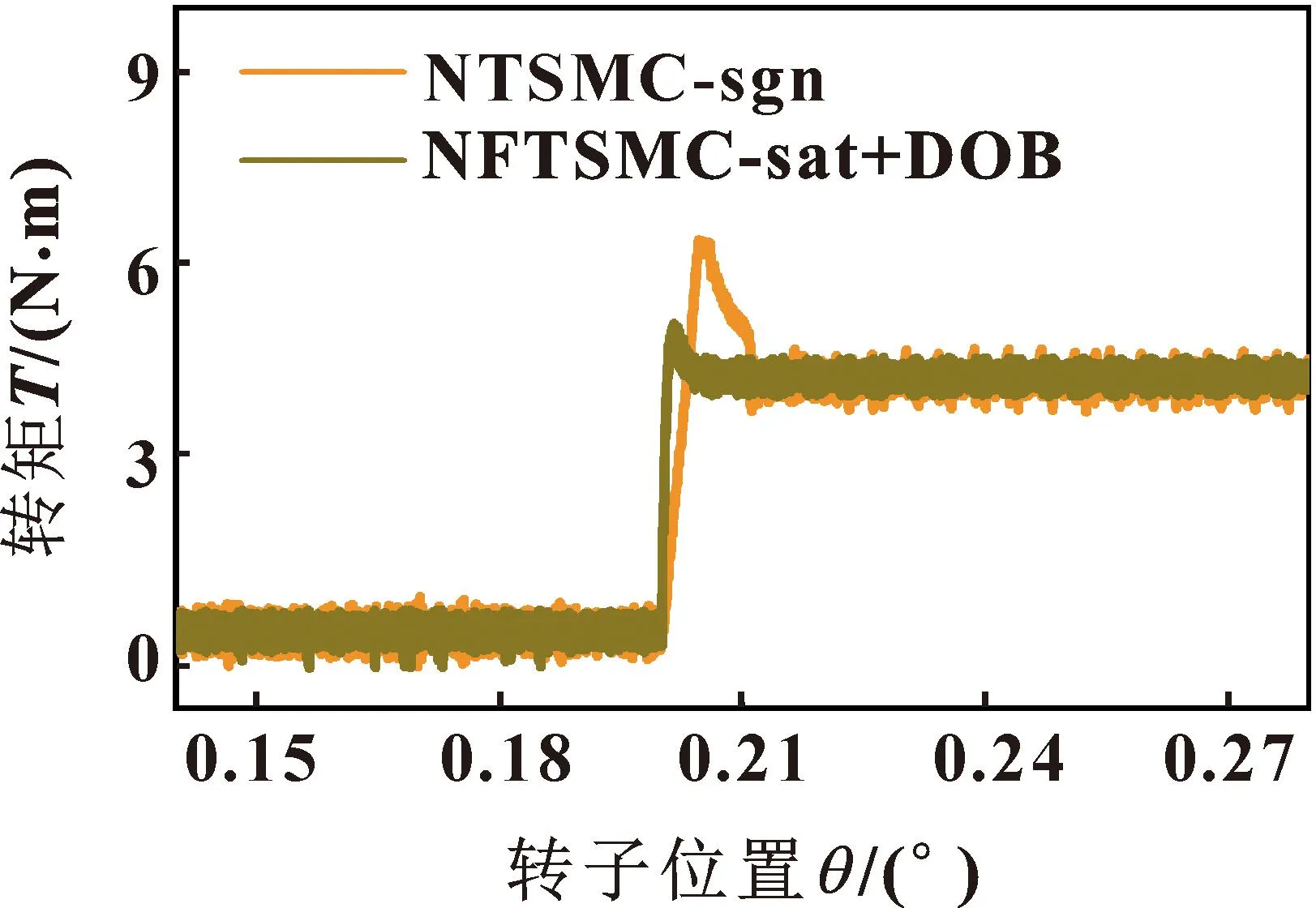
圖5 變負載工況永磁同步電機轉矩
4.3 變轉速工況性能仿真
在0.2 s時將參考轉速600 r/min突變為900 r/min,整個過程帶載運行,負載為2 N·m,基于兩種控制類型的變轉速工況電機電磁轉矩響應曲線如圖6所示。可知:采用基于符號函數的變指數趨近律非奇異終端滑模控制的電機,0.2 s轉速突變時,在0.208 s恢復穩定,但穩定運行時抖振較大;采用基于飽和函數的變指數趨近律非奇異快速終端滑模控制的電機電磁轉矩在0.205 s恢復穩定,恢復速度快,達到穩定時超調較小,穩定運行時轉矩波形較為平穩。
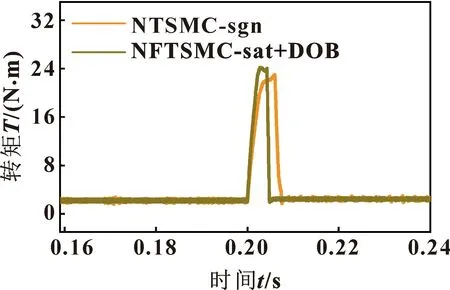
圖6 變轉速工況永磁同步電機轉矩
5 結論
(1)提出一種新型變指數趨近律滑模控制策略,并且將滑模趨近律中的符號函數替換成新型飽和函數,抑制了系統的抖振問題。
(2)針對外部擾動對滑模控制系統的影響,設計了非奇異快速終端滑模擾動觀測器,提升系統的抗干擾性能。
(3)仿真實驗結果表明:引入擾動觀測器的新型變指數趨近律滑模控制系統響應速度快、抖振小、抗干擾能力強,有較好的動態性能。

