基于神經(jīng)網(wǎng)絡(luò)相對增益陣的非線性系統(tǒng)常規(guī)控制回路配對
許鋒 劉文澤 劉聰 羅雄麟


基金項(xiàng)目:國家自然科學(xué)基金(批準(zhǔn)號:21676295)資助的課題。
作者簡介:許鋒(1976-),副教授,從事過程控制與系統(tǒng)工程方面的研究,xufeng@cup.edu.cn。
引用本文:許鋒,劉文澤,劉聰,等.基于神經(jīng)網(wǎng)絡(luò)相對增益陣的非線性系統(tǒng)常規(guī)控制回路配對[J].化工自動化及儀表,2023,50(6):000-000.
DOI:10.20030/j.cnki.1000-3932.202306000
摘? 要? 化工過程一般為非線性系統(tǒng),對其進(jìn)行常規(guī)控制系統(tǒng)結(jié)構(gòu)設(shè)計(jì)一般采用基于線性化模型的相對增益陣方法,但是當(dāng)非線性特性對控制性能影響較大時(shí),應(yīng)采用基于非線性模型的相對增益陣方法。筆者考慮非線性靜態(tài)環(huán)節(jié)與線性動態(tài)環(huán)節(jié)連接的Hammerstein模型,采用能量增益將線性動態(tài)環(huán)節(jié)轉(zhuǎn)換為靜態(tài)增益陣,與非線性靜態(tài)環(huán)節(jié)串聯(lián)為多變量非線性靜態(tài)增益陣,利用神經(jīng)網(wǎng)絡(luò)分別對組合后的非線性靜態(tài)增益陣的正向和逆向的映射關(guān)系進(jìn)行擬合,以訓(xùn)練好的正/逆神經(jīng)網(wǎng)絡(luò)求取非線性相對增益陣進(jìn)行常規(guī)控制回路配對。最后通過線性系統(tǒng)的實(shí)例分析驗(yàn)證了所提方法的正確性,并對酸堿中和反應(yīng)和精餾塔進(jìn)行了常規(guī)控制回路配對。
關(guān)鍵詞? 過程控制? PID控制? 多變量系統(tǒng)? 控制回路配對? 非線性系統(tǒng)
中圖分類號? TP13? ? ? ? ? 文獻(xiàn)標(biāo)志碼? A? ? ? ? ?文章編號? 1000-3932(2023)06-0000-00
化工過程一般為多變量系統(tǒng),即存在多個被控變量和多個操縱變量,因此多變量系統(tǒng)的內(nèi)部一般存在一定程度的耦合作用。考慮到控制安全可靠的要求,化工過程的底層控制系統(tǒng)主要采用常規(guī)PID控制,即將多變量系統(tǒng)分解為多個單入單出子系統(tǒng),分別設(shè)計(jì)PID控制回路,組成分散控制的多回路PID控制系統(tǒng)。
分散PID控制系統(tǒng)的各個控制回路之間如果存在比較嚴(yán)重的相互耦合作用,將難以達(dá)到較好的控制效果。因此,在進(jìn)行分散PID控制系統(tǒng)設(shè)計(jì)時(shí),首先要進(jìn)行控制系統(tǒng)的結(jié)構(gòu)設(shè)計(jì),即確定被控變量和操縱變量的配對,組成相應(yīng)的控制回路,而配對的原則是各個控制回路之間的相互耦合作用最小化,這樣才可以運(yùn)用成熟的經(jīng)典控制理論對各控制回路進(jìn)行單回路PID控制器設(shè)計(jì)。
多變量系統(tǒng)的關(guān)聯(lián)分析和控制回路配對問題的研究一般基于過程的線性模型,最早由BRISTOL E H于1966年提出相對增益陣(Relative Gain Array,RGA)方法[1]。WANG S和MUNRO N將其推廣到高維系統(tǒng)[2]。NIEDERLINSKI A提出了尼德林斯基指數(shù)(Niederlinski Index,NI)[3],與RGA配合使用,篩選不合適的控制回路配對。GROSDLDLER P等進(jìn)一步給出了RGA和NI閉環(huán)穩(wěn)定性的證明[4],該方法要求基于過程線性靜態(tài)增益陣計(jì)算RGA,在RGA中應(yīng)當(dāng)盡可能選擇大于零且接近于1的元素對應(yīng)的輸入輸出配對,即可保證控制回路之間的耦合最小化。
由于RGA忽略了系統(tǒng)的動態(tài)特性,因此在其基礎(chǔ)上提出了各種基于線性動態(tài)模型的改進(jìn)方法。RGA的動態(tài)改進(jìn)方法大體可以分為:基于開環(huán)階躍響應(yīng)的時(shí)域RGA[5~8]、基于頻率特性的頻域RGA[9~11]、基于最優(yōu)閉環(huán)控制器的動態(tài)RGA[12~14]、靜態(tài)信息與動態(tài)信息結(jié)合的組合RGA[15~20]。以上改進(jìn)方法中,時(shí)域RGA和頻域RGA都需要進(jìn)行時(shí)域或頻域積分求取平均值,計(jì)算量較大;而基于最優(yōu)閉環(huán)控制器的動態(tài)RGA,其配對結(jié)果依賴于閉環(huán)控制器的性能,需要對閉環(huán)控制器進(jìn)行最優(yōu)參數(shù)整定;組合RGA利用過程的帶寬、截止頻率、停留時(shí)間、時(shí)間常數(shù)及純滯后等信息與靜態(tài)增益陣相結(jié)合構(gòu)造含有動態(tài)信息的增益陣計(jì)算RGA,計(jì)算比較簡單,得到了廣泛應(yīng)用。
化工過程本質(zhì)上是非線性系統(tǒng),或多或少都含有非線性環(huán)節(jié)。對于非線性多變量系統(tǒng)的關(guān)聯(lián)分析和控制回路配對問題,針對弱非線性系統(tǒng),KADHIM A M H等采用最小二乘法辨識近似線性脈沖傳遞函數(shù)矩陣[21],XU C和SHIN Y C將模糊基礎(chǔ)函數(shù)網(wǎng)絡(luò)辨識結(jié)果線性化[22],創(chuàng)造應(yīng)用RGA方法的條件。當(dāng)非線性特性對控制性能影響較大時(shí),或隨著控制精度要求提高,原本可忽略的非線性特性必須予以考慮時(shí),這種情況下,就應(yīng)當(dāng)根據(jù)非線性環(huán)節(jié)的特征描述應(yīng)用相應(yīng)的關(guān)聯(lián)分析方法。針對仿射非線性系統(tǒng),DAOUTIDIS P和KRAVARIS C提出了基于相對階矩陣的配對準(zhǔn)則[23],相對階是對系統(tǒng)響應(yīng)慣性的一種衡量,因此每行中相對階最小的元素對應(yīng)的變量可組成配對;SHAKER H R和KOMAREJI M從系統(tǒng)可控、可觀性的角度思考控制回路配對問題,將仿射非線性系統(tǒng)可控、可觀格拉姆矩陣的乘積陣用于判斷每個子系統(tǒng)在整個大系統(tǒng)中的重要程度[24];GLAD S T等認(rèn)為RGA是正、逆系統(tǒng)的開環(huán)靜態(tài)增益之積[25,26],將靜態(tài)增益泛化為映射關(guān)系,被控變量經(jīng)開環(huán)系統(tǒng)逆向映射、正向映射后的異化情況可以用來衡量耦合程度。
Hammerstein非線性系統(tǒng)由一個非線性靜態(tài)環(huán)節(jié)后接一個動態(tài)線性環(huán)節(jié)構(gòu)成。在實(shí)際工業(yè)過程中,很多非線性系統(tǒng)都可被模擬為Hammerstein系統(tǒng),如熱交換器[27]、催化裂化裝置[28]、精餾塔[29~31]及pH酸堿中和過程[27]等。
基于線性動態(tài)模型的組合RGA方法中,文獻(xiàn)[20]提出的能量增益將靜態(tài)特性與線性動態(tài)特性分離,與Hammerstein非線性系統(tǒng)相似,因此筆者將Hammerstein系統(tǒng)的線性動態(tài)環(huán)節(jié)轉(zhuǎn)化為靜態(tài)的能量增益陣,再與非線性靜態(tài)環(huán)節(jié)相結(jié)合,形成等效的非線性靜態(tài)增益陣。然后筆者受文獻(xiàn)[25,26]的啟發(fā),利用人工神經(jīng)元網(wǎng)絡(luò)(Artificial Neural Network,ANN)擬合非線性靜態(tài)增益陣正向、逆向的映射關(guān)系,建立一個等效系統(tǒng),然后以訓(xùn)練好的正/逆神經(jīng)網(wǎng)絡(luò)求取非線性相對增益陣,考察被控變量經(jīng)過逆向映射和正向映射后的異化情況,以此進(jìn)行關(guān)聯(lián)分析和控制回路配對。
1非線性相對增益陣
對于如下多變量非線性靜態(tài)系統(tǒng):
其中,u為n維輸入變量,y為n維輸出變量,H為Rn到Rn的非線性映射關(guān)系。y0=H(u0)為系統(tǒng)的標(biāo)稱工作點(diǎn)。
當(dāng)除輸入uj外,其他輸入均保持在標(biāo)稱工作點(diǎn)(即其他回路開環(huán))時(shí),輸入uj對輸出yi的影響為:
其中,Hi為H的第i行。
如果非線性映射H可逆,令H-1為H的逆映射。當(dāng)除輸出yi外,其他輸出均保持在標(biāo)稱工作點(diǎn),即其他回路為閉環(huán)理想控制時(shí),需要保持當(dāng)前輸出yi所需的輸入uj為:
(3)
其中,為的第j行。
基于φij和ψji可定義非線性相對增益為:
(4)
非線性相對增益排列為陣列,得到非線性RGA為:
(5)
根據(jù)式(2)和式(3),可發(fā)現(xiàn)非線性RGA與輸出工作點(diǎn)有關(guān)。
當(dāng)非線性RGA滿足:
(6)
此時(shí)多變量非線性靜態(tài)系統(tǒng)式(1)是完全解耦的,即對于非線性RGA,第i行第j*列元素以斜率1單調(diào)變化,第i行其他元素保持不變時(shí),多變量非線性靜態(tài)系統(tǒng)是不存在內(nèi)部耦合的。非線性RGA與式(6)的異化程度,可以用來衡量多變量非線性系統(tǒng)的耦合程度。進(jìn)行控制回路配對時(shí),應(yīng)當(dāng)盡量選擇非線性RGA中變化斜率接近于1的元素對應(yīng)的輸入變量和輸出變量組成控制回路配對。
在工作區(qū)間內(nèi),繪出輸出yi與非線性相對增益λij的映射曲線。λij隨yi變化的斜率越接近1,表明uj對yi通道受其他通道的影響越小,應(yīng)當(dāng)選擇輸入變量uj和輸出變量yi組成控制回路配對。
由于對于非線性系統(tǒng),工作區(qū)間內(nèi)yi與非線性相對增益λij的映射曲線變化比較復(fù)雜,難以看清變化趨勢,為了進(jìn)行直觀的定量分析,基于yi與非線性相對增益λij的映射曲線上的離散點(diǎn),定義了平均非線性相對增益:
(7)
其中,{yi,1,…,yi,m,…,yi,N}為對輸出yi在其工作區(qū)間內(nèi)N組按升序排列的離散數(shù)據(jù),{λij,1,…,λij,m,…,λij,N}為對應(yīng)的非線性相對增益。
當(dāng)γij=1時(shí),表明λij隨yi變化的斜率為1;當(dāng)γij=0時(shí),表明λij保持不變;γij越接近1,表明uj對yi通道受其他通道的影響越小,應(yīng)當(dāng)選擇輸入變量uj和輸出變量yi組成控制回路配對。
對應(yīng)的平均非線性相對增益陣為:
(8)
平均非線性相對增益實(shí)際上是衡量了非線性相對增益λij與輸出yi的變化曲線與斜率為1曲線的平均偏離程度,由于非線性的影響,平均非線性相對增益陣無法具有與線性系統(tǒng)RGA完全相同的性質(zhì),如行元素和與列元素和等于1。但是,根據(jù)平均非線性相對增益陣選擇控制回路配對方案時(shí)也應(yīng)遵照以下規(guī)則:
a. 所有被選擇的變量配對對應(yīng)的γij取值必須是正數(shù);
b. 被選擇的變量配對的γij值應(yīng)盡量接近1。
2? Hammerstein系統(tǒng)等效非線性能量增益陣
Hammerstein非線性系統(tǒng)由非線性靜態(tài)環(huán)節(jié)后串聯(lián)線性動態(tài)環(huán)節(jié)組成,可表示為:
(9)
其中,u為n維輸入變量,y為n維輸出變量,H(u)為多變量非線性靜態(tài)映射,G(s)為多變量線性動態(tài)環(huán)節(jié)的傳遞函數(shù)矩陣。
H(u)可表示為:
(10)
G(s)可表示為:
(11)
對于多變量線性動態(tài)環(huán)節(jié)G(s),基于平方偏差積分,引入能量消耗的概念,定義輸入vj(t)對輸出yi的能量消耗大小為:
(12)
其中,eij(t)為輸入vj(t)作單位階躍輸入信號時(shí)輸出yi(t)與穩(wěn)態(tài)值yi(∞)之間的偏差歸一化后的值,即:
(13)
能量消耗只與過程的動態(tài)特性有關(guān),結(jié)合穩(wěn)態(tài)增益和能量消耗,能量增益定義為:
(14)
將所有輸入對輸出的能量增益組合起來,得到多變量線性動態(tài)環(huán)節(jié)G(s)的能量增益陣:
(15)
能量增益陣將多變量線性動態(tài)環(huán)節(jié)的傳遞函數(shù)矩陣G(s)等效為線性靜態(tài)增益陣,用能量增益陣KE取代多變量線性動態(tài)環(huán)節(jié)與非線性靜態(tài)環(huán)節(jié)H(u)串聯(lián),得到等效的多變量非線性靜態(tài)系統(tǒng)H*(u):
(16)
(17)
基于等效的多變量非線性靜態(tài)系統(tǒng)H*(u)計(jì)算非線性相對增益陣,以其作為控制回路配對和常規(guī)控制系統(tǒng)設(shè)計(jì)的依據(jù)。
3? 神經(jīng)網(wǎng)絡(luò)相對增益陣
要想計(jì)算非線性相對增益陣,就必須求得非線性靜態(tài)映射H*(u)的逆映射H*-1(y),但是非線性映射求取逆映射是非常困難的。由于BP神經(jīng)網(wǎng)絡(luò)具有很好的擬合非線性靜態(tài)映射的能力,因而用它分別對等效的多變量非線性靜態(tài)系統(tǒng)的正向、逆向映射關(guān)系進(jìn)行擬合。
對于已知的正向非線性系統(tǒng)H*(u),在給定的工作區(qū)間內(nèi)對輸入變量施加一系列隨機(jī)信號,產(chǎn)生一系列對應(yīng)的輸入輸出數(shù)據(jù)樣本{(yF,1,uF,1),(yF,2,uF,2),…,(yF,L,uF,L)}(下標(biāo)F指用于擬合的數(shù)據(jù))。
對于H*(u),以{uF,1,uF,2,…,uF,L}為輸入數(shù)據(jù)、{yF,1,yF,2,…,yF,L}為輸出數(shù)據(jù)訓(xùn)練正向神經(jīng)網(wǎng)絡(luò)NN_Ⅰ,就可以得到正向多變量非線性映射H*(u)。
對于H*-1(y),以{yF,1,yF,2,…,yF,L}為輸入數(shù)據(jù)、{uF,1,uF,2,…,uF,L}為輸出數(shù)據(jù)訓(xùn)練逆向神經(jīng)網(wǎng)絡(luò)NN_Ⅱ,就可以得到逆向多變量非線性映射H*-1(y)。
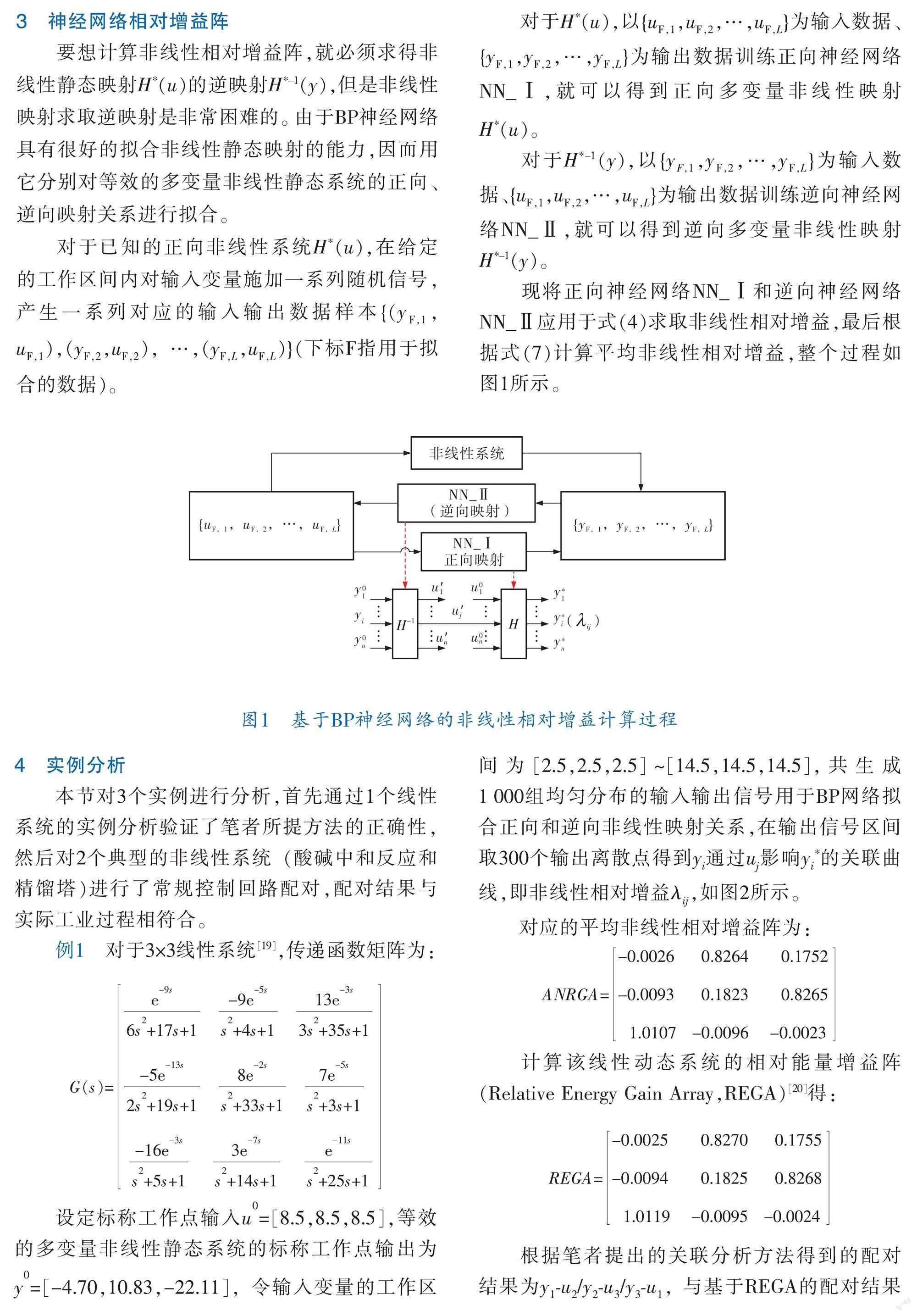
將正向神經(jīng)網(wǎng)絡(luò)NN_Ⅰ和逆向神經(jīng)網(wǎng)絡(luò)NN_Ⅱ應(yīng)用于式(4)求取非線性相對增益,最后根據(jù)式(7)計(jì)算平均非線性相對增益,整個過程如圖1所示。
圖1? 基于BP神經(jīng)網(wǎng)絡(luò)的非線性相關(guān)增益計(jì)算過程
4? 實(shí)例分析
本節(jié)對3個實(shí)例進(jìn)行分析,首先通過1個線性系統(tǒng)的實(shí)例分析驗(yàn)證了筆者所提方法的正確性,然后對2個典型的非線性系統(tǒng)(酸堿中和反應(yīng)和精餾塔)進(jìn)行了常規(guī)控制回路配對,配對結(jié)果與實(shí)際工業(yè)過程相符合。
例1? 對于33線性系統(tǒng)[19],傳遞函數(shù)矩陣為:
設(shè)定標(biāo)稱工作點(diǎn)輸入u0=[8.5,8.5,8.5],等效的多變量非線性靜態(tài)系統(tǒng)的標(biāo)稱工作點(diǎn)輸出為y0=[-4.70,10.83,-22.11],令輸入變量的工作區(qū)間為[2.5,2.5,2.5]~[14.5,14.5,14.5],生成1 000組均勻分布的輸入輸出信號用于BP網(wǎng)絡(luò)擬合正向和逆向非線性映射關(guān)系,在輸出信號區(qū)間取300個輸出離散點(diǎn)得到λij與yi的關(guān)聯(lián)曲線,如圖2所示。
圖2? 非線性相對增益曲線(例1)
對應(yīng)的平均非線性相對增益陣為:
計(jì)算該線性動態(tài)系統(tǒng)的相對能量增益陣(Relative Energy Gain Array,REGA)[20]得:
根據(jù)筆者提出的關(guān)聯(lián)分析方法得到配對結(jié)果為y1-u2/y2-u3/y3-u1,與基于REGA的配對結(jié)果相同,與文獻(xiàn)[19,20]的結(jié)論一致,由此驗(yàn)證了筆者所提方法的正確性。
例2? 對于酸堿中和反應(yīng)系統(tǒng)[27],其Hammerstein模型為:
其中,Xt為線性動態(tài)模型的狀態(tài)變量;Yt為線性動態(tài)模型的輸出變量;Ut為線性動態(tài)模型的輸入變量;ui*為非線性靜態(tài)模型的輸入,ui*通過非線性靜態(tài)模型轉(zhuǎn)化為Ut。
該酸堿中和反應(yīng)系統(tǒng)有2個操縱變量,分別為注入攪拌罐的酸液和堿液的流量;2個被控變量,分別為攪拌罐的液位與混合液的pH值。
眾所周知,酸堿中和反應(yīng)系統(tǒng)具有很強(qiáng)的非線性,在這種情況下,其配對方案依賴于具體的工作區(qū)間。實(shí)驗(yàn)選取了兩個測試工作區(qū)間,工作區(qū)間1的標(biāo)稱工作點(diǎn)輸入u0=[3,2.5],等效的多變量非線性靜態(tài)系統(tǒng)的標(biāo)稱工作點(diǎn)輸出為y0=[23.66,-6.24],令輸入變量的工作區(qū)間為[1.8,1.7]~[4.2,3.3];工作區(qū)間2的標(biāo)稱工作點(diǎn)輸入u0=[8,8],等效的多變量非線性靜態(tài)系統(tǒng)的標(biāo)稱工作點(diǎn)輸出為y0=[145.22,-115.56],令輸入變量的工作區(qū)間為[3,3]~[13,13]。從工作區(qū)間生成1 000組均勻分布的輸入輸出信號用于BP網(wǎng)絡(luò)擬合正向和逆向非線性映射關(guān)系,在輸出信號區(qū)間取300個輸出離散點(diǎn)得到λij與yi的關(guān)聯(lián)曲線,如圖3所示。
a. 工作區(qū)間1
b. 工作區(qū)間2
圖3? 非線性相對增益曲線(例2)
工作區(qū)間1的平均非線性相對增益陣計(jì)算結(jié)果為:
工作區(qū)間2的平均非線性相對增益陣計(jì)算結(jié)果為:
根據(jù)平均非線性RGA,工作區(qū)間1應(yīng)采取非對角配對方案,工作區(qū)間2應(yīng)采取對角配對方案。圖3亦直觀地佐證了相應(yīng)選擇,其配對方案對應(yīng)的λij與yi的關(guān)聯(lián)曲線斜率基本為正實(shí)數(shù)。此控制回路配對結(jié)果與工業(yè)過程實(shí)際情況是相符合的。
例3? 對于二元精餾塔系統(tǒng)[31],其Hammerstein模型為:
其中,輸出y1、y2分別表示塔底輕組分摩爾分率xB與塔頂輕組分摩爾分率xD的變化量;輸入u1、u2分別表示塔底再沸汽量V與塔頂回流量R的變化量,輸入最大變化量為穩(wěn)態(tài)值的±10%。
在本例中,標(biāo)稱工作點(diǎn)輸入u0=[0,0],等效的多變量非線性靜態(tài)系統(tǒng)的標(biāo)稱工作點(diǎn)輸出為y0=[0,0],令輸入變量的工作區(qū)間為[-0.5,-0.5]~[0.5,0.5],從工作區(qū)間生成1 000組均勻分布的輸入輸出信號用于BP網(wǎng)絡(luò)擬合正向和逆向非線性映射關(guān)系,在輸出信號區(qū)間取300個輸出離散點(diǎn)得到λij與yi的關(guān)聯(lián)曲線,如圖4所示。
圖4? 非線性相對增益曲線(例3)
平均非線性相對增益陣計(jì)算結(jié)果為:
分析圖4的關(guān)聯(lián)曲線與平均非線性相對增益陣,可以得到對角配對方案,即塔頂回流量控制塔頂產(chǎn)品的純度,塔底再沸汽量控制塔底產(chǎn)品純度,此控制回路配對結(jié)果符合精餾塔就近控制的一般性原則。
5? 結(jié)束語
針對Hammerstein系統(tǒng)具有動態(tài)特性與靜態(tài)特性分離的特點(diǎn),將Hammerstein系統(tǒng)的線性動態(tài)環(huán)節(jié)轉(zhuǎn)化為靜態(tài)的能量增益陣,再與非線性靜態(tài)環(huán)節(jié)相結(jié)合,形成等效的非線性靜態(tài)增益陣。再利用神經(jīng)網(wǎng)絡(luò)分別對組合的非線性靜態(tài)增益陣的正向和逆向的映射關(guān)系進(jìn)行擬合,以訓(xùn)練好的正/逆神經(jīng)網(wǎng)絡(luò)求取非線性相對增益陣,進(jìn)而計(jì)算工作區(qū)間內(nèi)的平均非線性相對增益陣,可以用與線性系統(tǒng)相對增益陣相似的方法完成控制回路配對。
由于非線性特性的影響,平均非線性相對增益陣與工作區(qū)間有關(guān)。對于線性系統(tǒng)和弱非線性系統(tǒng),可以得到統(tǒng)一的控制回路配對結(jié)果;而對于強(qiáng)非線性系統(tǒng),控制回路配對結(jié)果與工作區(qū)間有關(guān),當(dāng)工作區(qū)間發(fā)生大范圍變化時(shí),控制回路配對結(jié)果將不適用,需要重新進(jìn)行常規(guī)控制系統(tǒng)結(jié)構(gòu)設(shè)計(jì)。因此,對于強(qiáng)非線性系統(tǒng),務(wù)必將工作點(diǎn)控制在合理的工作區(qū)間,脫離工作區(qū)間將導(dǎo)致系統(tǒng)發(fā)生故障。
參? 考? 文? 獻(xiàn)
[1]BRISTOL E H.On a new measure of interaction for multivariable process control[J].IEEE Transactions on Automatic Control,1966,11(1):133-134.
[2]WANG S,MUNRO N.A complete proof of Bristol's relative gain array[J].Transactions of the Institute of Measurement & Control, 1982, 4(1): 53-56.
[3]NIEDERLINSKI A.A heuristic approach to the design of linear multivariable interacting control systems[J].Automatica,1971,7(6):691-701.
[4]GROSDLDLER P,MORARI M,HOLT B R.Closed-loop properties from steady state gain information[J].Industrial & Engineering Chemistry Fundamentals,1985,24(2):221-235.
[5]WITCHER M F, MCAVOY T J.Interaction control system:Steady state and dynamic measurement of interaction[J].ISA Transactions, 1977,16(3): 35-41.
[6]GAGNEPAIN J P,SEBORG D E.Analysis of process interactions with application to multiloop control system design[J].Industrial & Engineering Chemistry Process Design and Development,1982,21(1):5-11.
[7]葉凌箭,宋執(zhí)環(huán).多變量控制系統(tǒng)的一種變量配對方法[J].控制與決策,2009,24(12):1795-1800.
[8]羅雄麟,任麗紅,周曉龍,等.常規(guī)控制系統(tǒng)配對設(shè)計(jì)的動態(tài)相對增益陣研究[J].化工自動化及儀表,2012,39(3):295-300.
[9]許鋒,潘琦,王一嵐,等.工業(yè)過程多變量系統(tǒng)常規(guī)控制結(jié)構(gòu)的頻域設(shè)計(jì)[J].清華大學(xué)學(xué)報(bào),2016,56(4):448-452.
[10]許鋒,袁未未,羅雄麟.化工過程非方瘦系統(tǒng)的串級控制系統(tǒng)結(jié)構(gòu)設(shè)計(jì)[J].化工學(xué)報(bào),2017,68(7):2833-2843.
[11]許鋒,袁未未,羅雄麟.大系統(tǒng)的常規(guī)控制系統(tǒng)結(jié)構(gòu)設(shè)計(jì)[J].計(jì)算機(jī)與應(yīng)用化學(xué),2017,34(9):661-668.
[12]MEEUSE F M,HUESMAN A E M.Analyzing dynamic interaction of control loops in the time domain[J].Industrial & Engineering Chemistry Research,2002,41(18):4585-4590.
[13]MCAOY T,ARKUN Y,CHEN R,et al.A new approach to defining a dynamic relative gain[J].Control Engineering Practice,2003,11(8):907-914.
[14]XU F,CAO P F,LUO X L.Regulator configuration design by means of model predictive control[J].Journal of Process Control,2015,28:95-103.
[15]XIONG Q,CAI W J,HE M J.A practical loop pairing criterion for multivariable processes[J].Journal of Process Control,2005,15(7):741-747.
[16]XIONG Q,CAI W J,HE M J, et al.Decentralized control system design for multivariable processes—A novel method based on effective relative gain array[J].Industrial & Engineering Chemistry Research,2006,45(8):2769-2776.
[17]XIONG Q,CAI W J.Effective transfer function method for decentralized control system design for multi-input multi-output processes[J].Journal of Process Control,2006,16(8):773-784.
[18]XIONG Q,CAI W J,HE M J.Equivalent transfer function method for PI/PID controller design of MIMO processes[J].Journal of Process Control,2007,17(8):665-673.
[19]HE M J,CAI W J,NI W,et al.RNGA based control system configuration for multivariable processes[J].Journal of Process Control, 2009,19(6):1036-1042.
[20]任麗紅,劉雨波,羅雄麟,等.多變量時(shí)滯系統(tǒng)的關(guān)聯(lián)分析與變量配對[J].化工自動化及儀表,2012,39(6):743-746.
[21]KADHIM A M H,MIGUEL C A,BIRK W.Relative gain array of weakly nonlinear systems using a nonparametric identification approach[C]//2015 IEEE Conference on Control Applications(CCA).Piscataway,NJ:IEEE,2015:1612-1617.
[22]XU C,SHIN Y C. Interaction analysis for MIMO nonlinear systems based on a fuzzy basis function network model[J].Fuzzy Sets and Systems,2007,158(18):2013-2025.
[23]DAOUTIDIS P,KRAVARIS C.Structural evaluation of control configurations for multivariable nonlinear process[J].Chemical Engineering Science,1992,47(5):1091-1107.
[24]SHAKER H R,KOMAREJI M.Control configuration selection for multivariable nonlinear systems[J].Industrial & Engineering Chemistry Research,2012,51(25):8583-8587.
[25]GLAD S T.Extensions of the RGA concept to nonlinear systems[C]//European Control Conference(ECC).Piscataway,NJ:IEEE,1999:961-963.
[26]MOAVENI B,KHAKISEDIGH A.Input-output pairing for nonlinear multivariable systems[J].Journal of Applied Sciences,2007,7(22):3492-3498.
[27]LAKSHMINARAYANAN S,SHAH S L,NANDAKUMAR K. Identification of Hammerstein models using multivariate statistical tools[J].Chemical Engineering Science,1995,50(22):3599-3613.
[28]HARNISCHMACHER G,MARQUARDT W.A multi-variate Hammerstein model for processes with input directionality[J].Journal of Process Control,2007,17(6):539-550.
[29]BIAGIOLA S I,F(xiàn)IGUEROA J L.Identification of uncertain MIMO Wiener and Hammerstein models[J].Computers and Chemical Engineering,2011,35(12):2867-2875.
[30]G?MEZ J C,BAEYENS E.Identification of block-oriented nonlinear systems using orthonormal bases[J].Journal of Process Control,2004,14(6):685-697.
[31]FRUZZETTI K P,PALAZO?LU A,MCDONALD K A.Nolinear model predictive control using Hammerstein models[J].Journal of Process Control,1997,7(1):31-41.
(收稿日期:2022-10-31,修回日期:2023-06-25)

