基于混合優化算法的超參數優化方法及其應用

作者簡介：丁彧洋（1997-），碩士研究生，從事深度學習、時間序列分析的研究，6201905018@stu.jiangnan.edu.cn。

引用本文：丁彧洋.基于混合優化算法的超參數優化方法及其應用[J].化工自動化及儀表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘? 要? 卷積神經網絡（CNN）自身結構的超參數對于分類問題中的準確率與效率有較大的影響，針對現有超參數優化方法多依賴傳統組合，優化結果不徹底，導致模型分類效果不佳的狀況，提出一種基于混合優化算法的CNN超參數優化方法。該方法根據CNN架構的結構特點選取超參數，然后采用粒子群優化算法（PSO）-梯度下降（GD）混合算法進行優化。在測試數據集上的實驗結果表明：該方法在分類問題上具有較好的性能，提升了超參數的優化效率，避免了傳統PSO算法易陷入局部最優的缺點。

關鍵詞? PSO-GD混合算法? 超參數優化? CNN? 分類性能? 優化效率? 局部最優

中圖分類號? TP183? ? ? 文獻標志碼? A? ? ? 文章編號? 1000-3932（2023）06-0000-00

現階段，信息分類技術已經發展得比較成熟，適用于不同場景的卷積神經網絡（Convolutional Neural Network，CNN）架構[1～4]層出不窮，但復雜的CNN結構往往耗費硬件資源及計算成本。CNN用于分類任務訓練前，需提前設置好CNN內部的一些參數（即超參數），選取一組最優超參數可以在不改變CNN結構的前提下最大程度地提升CNN的分類性能。因此，選定適合的超參數將CNN架構的分類性能完全釋放出來，在工程實踐中具有極其重要的作用和意義。

相關CNN超參數優化方法的研究已經有一些成果，早期研究集中于將機器學習的超參數優化方法用于CNN[5]。超參數優化方法主要分為無模型優化和基于模型的優化，目前，前者最先進的方法包括簡單的網格和隨機搜索；后者包括基于種群的啟發式優化算法，以及基于高斯過程的貝葉斯優化（GP）[6]。啟發式優化算法對于CNN超參數優化尤為值得關注，其中粒子群優化算法（Particle Swarm Optimization，PSO）[7，8]由于其簡單性和通用性已經被證明在解決許多區域中的多任務方面非常有效，并且它具有大規模并行化的巨大潛力。基于PSO的超參數優化，其搜索效率遠超網格搜索、隨機搜索等，縮短了超參數優化的搜索時間，解決了傳統超參數優化效率低、耗時長等問題。但PSO也存在易陷入局部最優的問題，這會造成超參數優化停留在局部最優而非全局最優的一組超參數，在一定程度上無法搜索到使CNN性能達到最優的一組超參數，從而無法使CNN處理分類問題時達到最理想的結果。由此，混合優化算法合成為新趨勢之一，通過將不同的元啟發算法進行結合，綜合不同元啟發式算法的特性，使混合算法擁有更快的尋優速度或更好的尋優特性。文獻[9]探索了一種遺傳算法+PSO的混合算法，該算法對優化問題有顯著效果；文獻[10]提出一種模擬退火和梯度結合的混合算法，該混合算法為模型提供了概率爬坡的能力，在不犧牲模型收斂效率和穩定性的情況下具有更好的泛化效果。如今，混合算法更傾向于針對具體問題進行混合和改進，文獻[11]為特征選擇問題提出一種混合灰狼優化和粒子群優化的二進制形式算法，用以獲得更優的特征性能指標和使用精度；文獻[12]針對具有有限函數計算的計算成本數值問題，提出混合螢火蟲和粒子群優化算法，通過檢查前期的全局最佳適應度值，正確確定了本地搜索過程的開始點位。

筆者提出一種基于粒子群優化算法（PSO）-梯度下降（Gradient Descent，GD）混合優化算法的CNN超參數優化方法，根據CNN的架構特點選取卷積層與池化層的結構參數，以避免傳統PSO對超參數的優化停留在局部最優的弊端。

1? CNN及其超參數優化算法

1.1? CNN

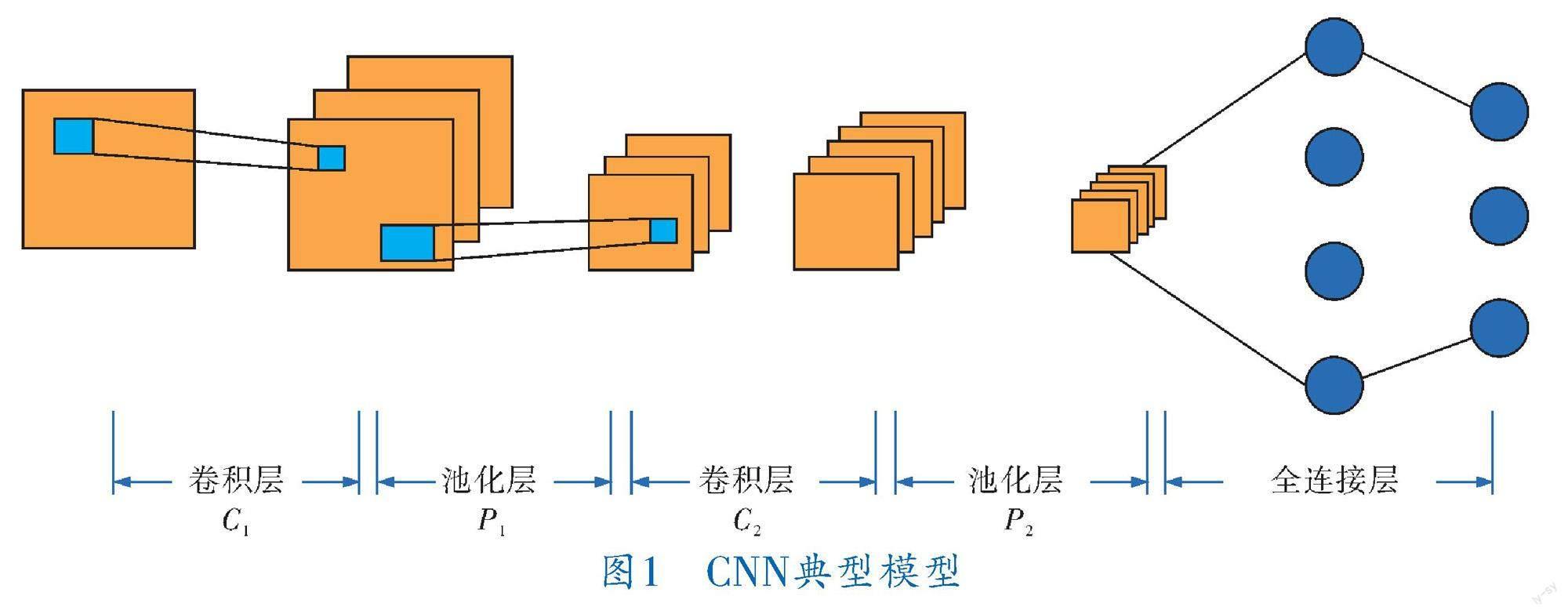
CNN作為前饋神經網絡，其概念主要來自信號處理領域的卷積，實際表征了輸入與輸出間的映射關系，典型模型如圖1所示，其結構主要包括卷積層、池化層以及激活函數等，由卷積層對輸入值間存在的耦合關系進行處理，激活函數保證整個模型能夠較好地擬合非線性函數，而全連接層則進一步提高網絡的擬合能力。

1.2? 混合智能優化算法

混合智能優化算法是將啟發式算法與梯度算法相結合，其本質上是隨機的，因為它依賴于啟發算法繞過局部極小值，類似于對未知數的連續隨機擾動，并且能夠以正概率“逃離”任何陷阱。同時，對于小鄰域，它能以極快的速度收斂到局部極小值，大幅提高隨機優化算法的搜索效率和收斂速度。

由于PSO始于解的一個種群（多點）而非單個解，因此具有更好的全局尋優能力。采用概率而不是確定的狀態轉移規則，能自適應地調整搜索方向，因此能更好地跳出局部最優點。而GD算法則采用負梯度作為極值的搜索方向，以便能夠在搜索區間內最快速下降，這樣與初值點選取的好壞關系減小，又由于GD算法每次的迭代計算量小，在經過有限量次迭代后目標函數值都能夠大幅下降、程序簡短，并且占用較少的時間資源和運算資源。因此，筆者將兩種算法結合，提出PSO-GD混合優化算法，其流程如圖2所示，先采用GD算法找到局部最優點，再采用PSO算法尋找最優解。同時，如果算法陷入局部最優點，PSO能跳出局部最優點再次尋找全局最優點。

2? 基于PSO-GD算法的CNN超參數優化方法

2.1? 算法基本原理

根據圖2所示的完整算法流程，可大致將PSO-GD混合智能優化算法描述為：

a.隨機生成并評估。令迭代數。

b.通過基于梯度的最小化方法求解局部最小值，并作為初始猜測給出，，其中，是閾值，設定為接近零值的正參數。

c.從開始，執行次模擬粒子群發散直到獲得一個點，使得對于誤差精度滿足。

d.。回到步驟b循環，直到收斂。

在算法的步驟c中，模擬的粒子群迭代由4個關鍵步驟組成，即：

a.下一個實驗點主要是由已知解的附近空間的粒子運動產生的；

b.將粒子群個體特征轉換為二進制數字，確定它們的值范圍和邊界條件；

c.通過改變新一代分布來控制是否跳出局部最優極限；

d.結合粒子群變異和交叉的特點，在迭代過程中獲得最適合個體的最優解，終止迭代并輸出最終結果。

2.2? 算法收斂性分析

2.2.1? 標準PSO算法的全局收斂性

首先描述PSO的迭代過程：

a.初始化，隨機查找且設；

b.從已有的粒子值中隨機生成新的極值；

c.設，再選擇，設（其中（·）為迭代函數，，且是的任意Borel子集），返回步驟b迭代。

條件1? ，并且若，則有。

條件2? 對中的任意Borel子集，且，有。

定理1? PSO算法不滿足條件1。

定理2? PSO算法不滿足條件2，不能保證全局收斂性。

因此可得出結論，該算法作為隨機搜索算法，當粒子尚未搜索到最優區域時，粒子的發散速度就可能已經失去動力，進而導致無法跳出局部最優，即不能得到全局最優。而從整體來看，應該分析最優保持操作，所以最優保持操作需由梯度算法實現，從而需要進一步分析梯度算法得出的結果。

2.2.2? GD算法的收斂性

首先，由數學理論可以得到以下定義和定理。

如果標量函數滿足如下條件，稱其滿足Lipschitz連續性條件：

（1）

其中，為Lipschitz常數。對于固定的，是一個定值。這個條件對函數值的變化做出了限制。

如果函數的梯度滿足值為的Lipschitz連續，稱函數為平滑：

（2）

這個條件對函數梯度的變化進行了約束：梯度之差的模長不會超過自變量之差模長的常數倍。滿足平滑的函數有如下性質：

（3）

如果函數為凸函數，過的切線在曲線下，則有：

（4）

進而。

因此得出平滑具有兩個性質：

（5）

（6）

首先證明GD算法的自變量的新解比當前解更接近最終解。考慮新解到最終解的距離：

（7）

利用平滑的第2點性質（即式（6）），考慮在點的線性擬合：

（8）

由于為最終解，則有：

（9）

（10）

（11）

代入式（7），有：

（12）

顯然，只要學習率，就可以保證：

（13）

然后，考慮兩次迭代的函數值：

（14）

插進最優解的函數值，比較兩次迭代距最優點函數值的距離：

（15）

利用凸函數性質以及柯西-施瓦茨不等式，構造一個關系：

（16）

（17）

代入式（15）可得：

（18）

從之前的證明可以得到，于是除去分母中的，則有：

（19）

然后兩邊同時除以正數得到：

（20）

然后對式（20）從0～t-1進行累加：

（21）

由于：

（22）

所以：

（23）

由此證明完畢，即算法的收斂性成立。

2.3? CNN超參數優化建模

首先對需要分類的數據集進行預處理，并將其按比例劃分成訓練集T、測試集和驗證集V，其中驗證集是從訓練集中提取的，滿足。

在準備工作完成后，開始搭建CNN架構，包括卷積層、池化層、卷積層、池化層，最后由Softmax激活終止。根據CNN架構的結構特點，選取卷積層C1和池化層P1的結構參數為后決定的超參數，并確定這組超參數的取值范圍為。

而后在驗證集V上采用PSO-GD混合算法優化CNN架構的超參數，可得一組對應的超參數值，整個超參數優化過程設計到的相關變量見表1。

在第次迭代時，每個粒子更新自己的速度和位置：

（24）

（25）

其中，為慣性因子，和為學習因子，均為自選常數；和是范圍內的隨機數。

隨后選擇全局變異算子對整個群體中的所有粒子的位置進行變更，或者選擇局部變異算子對群體中的精英粒子的位置進行變更。全局變異算子與局部變異算子對位置變更的公式為：

（26）

（27）

其中，是波動因子；為范圍內的隨機數；為精英粒子；是由局部變異算子生成的新粒子的數目；為全局變異頻率；為局部變異頻率。

之后，檢查粒子速度和位置是否越界，若越界則以其超出的邊界值取代相應的粒子值。設為粒子的速度范圍，為粒子的位置范圍。具體判斷方法如下：

a.若，則；

b.若，則；

c.若，則；

d.若，則。

根據上述限制條件確定的最優位置即所要求的超參數值。將超參數輸入到CNN中，并用最初得到的訓練集對優化后的CNN進行訓練，而將初始步驟得到的測試集輸入訓練好的CNN中，可以得到最終結果。

隨后根據條件，判斷迭代是否達到終止條件。

首先計算各個粒子的適應度函數值：

（28）

其中，為先前階段得到的分類結果的準確率。

通過式（28）得到的本次迭代的各個粒子適應度函數值，分別更新個體歷史最優位置和群體最優位置，得到本次迭代最優粒子：

（29）

（30）

判斷最優粒子的適應度值增加小于閾值，判斷群體中的最佳粒子位置更新小于最小步長，判斷迭代次數是否達到最大迭代次數，若滿足上述終止條件之一，則終止迭代。如果沒有達到終止條件，則重新代回超參數值確定步驟起始段繼續流程，如果達到終止條件，得到最終的最優超參數，記為，并將其代入到CNN結構中，對整個數據集的進行分類，得到最終結果。

3? 仿真實驗與結果分析

為了驗證基于PSO-GD混合優化算法的CNN超參數優化方法的性能，選取兩個基準測試數據集進行實驗仿真，其中手寫數字識別MNIST數據集的片段如圖3所示，該數據集有70 000個灰度圖像，每個圖像像素為28×28，其中包含10個類別，每個類別有7 000個圖像；隨機選取該數據集中的60 000個圖像作為訓練集，剩余的10 000個圖像作為測試集，從訓練集中隨機挑選出6 000個圖像作為驗證集。

物體識別cifar-10數據集的片段如圖4所示，該數據集有60 000個32×32像素的彩色圖像，其中包含10個類別，每個類別有6 000個圖像；隨機選取該數據集中的50 000個圖像作為訓練集，剩余的10 000個圖像作為測試集，從訓練集中隨機挑選出5 000個圖像作為驗證集。

3.1? MNIST數據集實驗

將混合優化算法中的參數定為粒子搜索空間維度，粒子個數，慣性因子，學習因子，閾值，最小步長，判斷迭代次數。搭建CNN架構，選取卷積層C1和池化層P1的結構參數為超參數，確定這組超參數的取值范圍，見表2。

在算法結構中，將輸出結果以適應度函數的值進行表示，由于過程包含收斂性的分析，因此整體結果按相反數取值，因此，適應度函數值越大，分類效果越好。

MNIST數據集的分類結果如圖5所示。

3.2? cifar-10數據集實驗

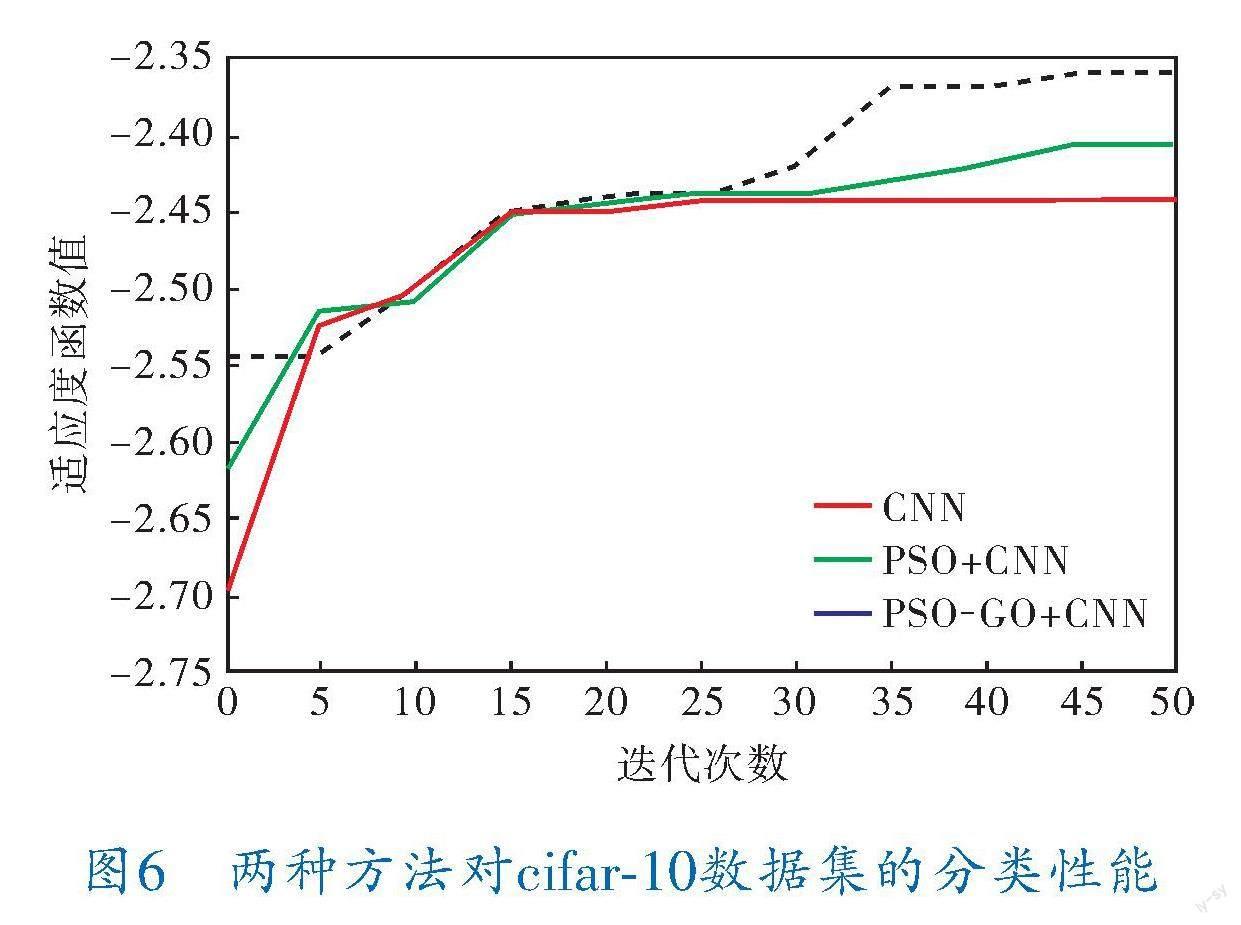
實驗所選取各參數與MNIST數據集實驗相同，分類結果如圖6所示。

對比圖5、6可以看出，無論是超參數優化前的常規CNN，還是PSO、PSO-GD優化超參數后的CNN，隨著迭代次數的增加，優化都在逐步進行，分類誤差不斷減小，而經過超參數優化后的方法，在分類準確性上有所提高。

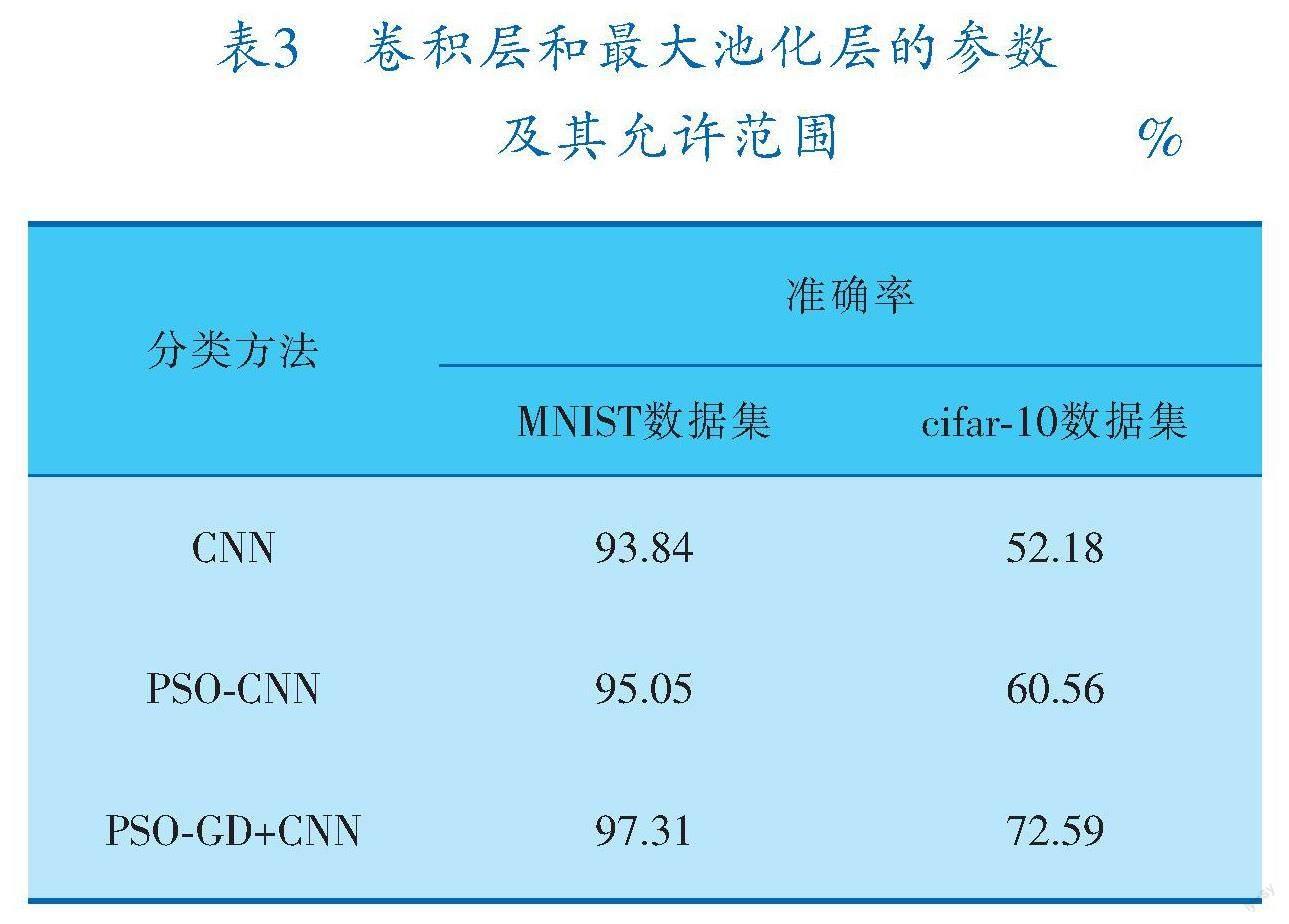
超參數優化方法改進前后手寫數字識別MNIST數據集和物體識別cifar-10數據集圖像分類準確率對比見表3，可以看出，PSO-GD混合優化方法在不改變分類CNN架構的前提下對圖像分類準確率有一定程度的提升，最大程度地發揮了CNN架構的圖像分類潛力，節約了CNN進行圖像分類時的硬件資源及計算成本。

4? 結束語

利用PSO的全局搜索性能融合GD算法的快收斂性，提出基于PSO-GD混合優化算法的超參數優化方法，對CNN結構中的超參數進行了優化，并通過典型的測試數據集對其分類性能進行了評價。實驗結果表明，該方法與優化前相比，具備了更好的跳出局部最優限制的能力，最大程度地發揮了CNN架構的分類潛力，節約了CNN進行分類任務時的硬件資源及計算成本，該方法具有一定工程應用價值。

參? 考? 文? 獻

[1] SIMONYAN K，ZISSERMAN A.Very deep convolutional networks for large-scale image recognition[C]//Proceedings of? the? 3rd? International? Conference? on? Learning Representations.San Diego：ICLR，2015：1-14.

[2] KRIZHEVSKY A，SUTSKEVER I，HINTON G E.Imagenet classification with deep convolutional neural networks[J].Communications of the ACM，2017，60（6）：84-90.

[3] GIRSHICK R，DONAHUE J，DARRELL T，et al.Rich feature hierarchies for accurate object detection and semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2014：580-587

[4] REDMON J，DIVVALA S，GIRSHICK R，et al.You only look once：Unified，real-time object detection[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2016：779-788.

[5] ANDONIE R，FLOREA A C.Weighted random search for CNN hyperparameter optimization[J].arXiv preprint arXiv：2003.13300，2020.

[6] WU J，CHEN X Y，ZHANG H，et al.Hyperparameter optimization for machine learning models based on Bayesian optimization[J].Journal of Electronic Science and Technology，2019，17（1）：26-40.

[7] WANG D，TAN D，LIU L.Particle swarm optimization algorithm： an overview[J].Soft computing，2018，22：387-408.

[8] SALLEH I，BELKOURCHIA Y，AZRAR L.Optimization of the shape parameter of RBF based on the PSO algorithm to solve nonlinear stochastic differential equation[C]//2019 5th International Conference on Optimization and Applications （ICOA）.2019：1-5.

[9] GHORBANI N，KASAEIAN A，TOOPSHEKAN A，et al.Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability[J].Energy，2018，154：581-591.

[10] CAI Z.SA-GD：Improved Gradient Descent Learning Strategy with Simulated Annealing[J].arXiv preprint arXiv：2107.07558，2021.

[11] AL-TASHI Q，KADIR S J A，RAIS H M，et al.Binary optimization using hybrid grey wolf optimization for feature selection[J].Ieee Access，2019（7）：39496-39508.

[12] AYDILEK I B.A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems[J].Applied Soft Computing，2018，66：232-249.

（收稿日期：2023-02-17，修回日期：2023-03-22）