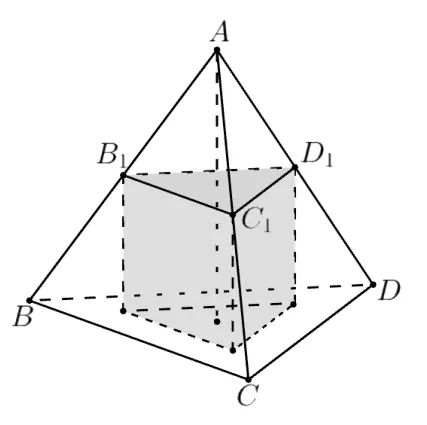
什么樣的圓柱和圓錐可以放入正方體及正四面體內?
深圳市龍華區教育科學研究院附屬外國語學校(518109)鐘文體
1 問題呈現
2023 年新課標I 卷第12 題是一道源于生活的立體幾何問題(物品裝箱問題).題目以正方體為載體,涉及正方體的面對角線、體對角線、最大截面、內接球、內接四面體、內接圓柱以及它們的位置關系等知識,綜合性較強.原題的一個亮點是沒有給出圖形,而正方體、正四面體、圓柱、球等都是數學中常見的“空間想象的支架”[1],也是生活中隨處可見的圖形.此題要求學生以“支架”為支撐構建空間圖形,需要較強的空間想象的能力.筆者認為,不給出圖形恰是此題的點睛之筆,以便更好地考察直觀想象和邏輯推理等數學學科核心素養.此外,要想順利解答此題還需要一定的數據估計能力.原題如下:
試題下列物體中,能夠被整體放入棱長為1(單位: m)的正方體容器(容器壁厚度忽略不計)內的有( )
A.直徑為0.99m 的球體
B.所有棱長均為1.4m 的四面體
C.底面直徑為0.01m,高為1.8m 的圓柱體
D.底面直徑為1.2m,高為0.01m 的圓柱體
解析對于A 選項,因為棱長為1m 的正方體的內接球直徑為1m,而0.99m < 1m,所以直徑為0.99m 的球體可以放入棱長為1m 的正方體內,A 正確.
對于D 選項, 忽略0.01m 的厚度, 將圓柱近似為直徑為1.2m 的二維圓盤, 則問題轉化為直徑為1.2m 的圓能否放入棱長為1m 的正方體內.考慮正方體的最大截面EFGHIJ, 這是一個正六邊形, 其頂點為正方體棱的中點,如圖1 所示.可算出正六邊形EFGHIJ的內切圓直徑為,所以直徑為1.2m 的圓可以放入棱長為1m 的正方體內,D 正確.
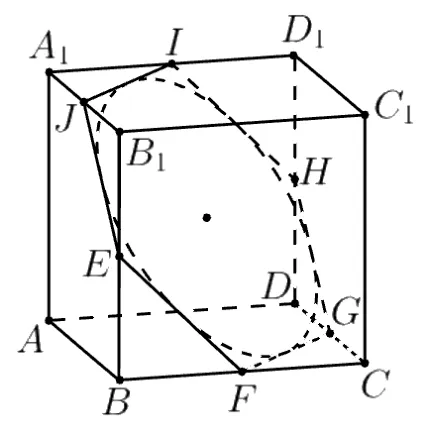
圖1
以上對A、B、C 選項的解析都符合數學的嚴謹性,無可挑剔.對于D 選項,以上呈現的解析是網絡上比較流行的“秒殺”方法, 適合在考場上使用.但嚴格來說,這樣的做法其實是站不住腳的,“將0.01m 的厚度忽略”在數學上缺乏嚴謹性.例如, 若將D 選項的圓柱厚度改為0.02m、0.03m、0.04m 等等,那么還能忽略厚度嗎? 作為教師,我們應對D 選項進行嚴謹的理性分析,切不可模棱兩可.
2 什么樣的圓柱可以放入正方體內?
我們提出以下更一般的問題.
問題1什么樣的圓柱可以放入棱長為a的正方體內?
顯然, 若底面半徑為r, 高為h的圓柱可以放入正方體內,則底面半徑不超過r,高不超過h的圓柱都可放入正方體內.因此,只需探討什么樣的圓柱恰好可以放入正方體即可,這里的“恰好放入”是指圓柱的面或邊緣與正方體的接觸面是緊貼著的,類似于兩條曲線的相切.我們也稱圓柱和正方體的這種位置關系為圓柱內接于正方體.
首先,底面直徑和高都為a的圓柱恰好可以放入棱長為a的正方體內,此時,只需將圓柱底面圓心與正方體其中一個側面的中心重合,且圓柱的高與此側面垂直即可,如圖2 所示.我們稱這種放入方式為圓柱正接于正方體內.
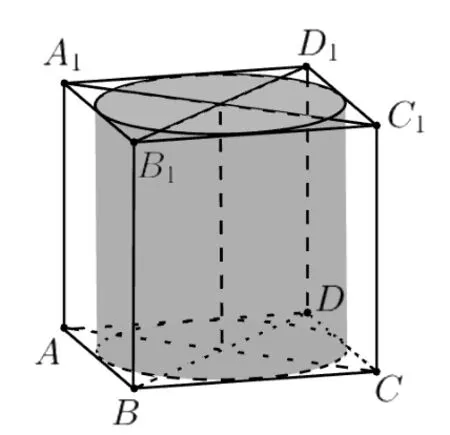
圖2
另一種方式是斜接,圓柱的底面圓心連線與正方體的體對角線重合, 圖3 和圖4 展示了兩種典型情形, 分別為“扁平”型和“細長”型.
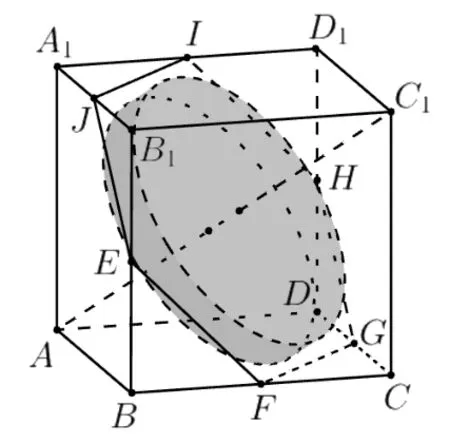
圖3

圖4
那么, 當圓柱斜接于正方體內時, 圓柱的高和底面半徑之間有什么關系呢? 如圖5, 設圓柱底面半徑為r,底面圓心為O, 圓柱與正方體上底面的接觸點為P, 根據對稱性可知點P在正方體的面對角線A1C1上.易知,, 從而.因此, 圓柱的高.于是,我們得到了正方體斜接圓柱的底面半徑和其高的關系.根據這一關系可知,當r= 0.6時,,從而原題的D 選項正確.至此,我們給出了D 選項的嚴謹解釋.
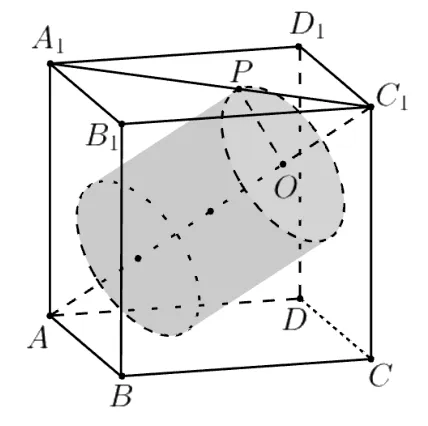
圖5
根據上面得到的關系,還可以求出斜接于正方體的圓柱體積的最大值.事實上,圓柱體積
求導得
3 什么樣的圓錐可以放入正方體內?
對經典試題進行變式、聯想、遷移可以幫助學生更深入、透徹地理解問題的本質,也有助于培養發散思維,提高問題解決能力.圓錐也是常見的“空間想象的支架”[1]之一,以上解決了正方體內接圓柱問題,下面用類似的方法解決正方體內接圓錐問題.
問題2什么樣的圓錐可以放入棱長為a的正方體內?
類似前面,只考慮恰好可以放入的情形.也分為正接(圖6)和斜接兩種方式(圖7).正接較為簡單,以下討論斜接情形.如圖7,設圓錐底面半徑為r,底面圓心為O,圓錐與正方體下底面的接觸點為P,類似前面可知.因此,圓錐的高.于是,我們得到了正方體斜接圓錐的底面半徑和其高的關系.

圖6

圖7
根據這一關系,還可以求出斜接于正方體的圓錐體積的最大值.事實上,圓錐體積
從而V(r)單調遞增,故當時,斜接于正方體的圓錐體積取最大值.此時,圓錐的底面為正方體最大截面的內切圓,如圖8 所示.
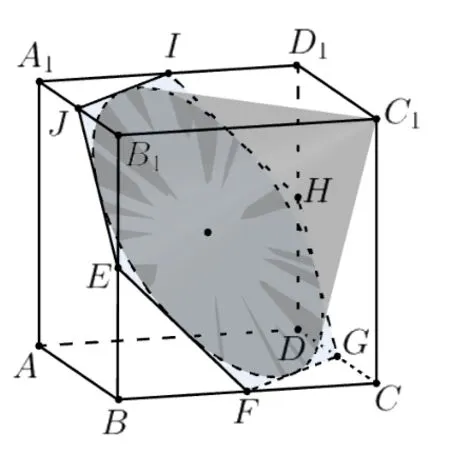
圖8
4 什么樣的圓柱可以放入正四面體內?
正四面體是另一種常見的正多面體,下面將以上方法類比到正四面體中.
問題3什么樣的圓柱可以放入棱長為a的正四面體內?
同樣只考慮恰好可以放入的情形.為此,先回顧正三角形和正四面體中的一些有用的數量關系.
結論1邊長為a的正三角形的內切圓半徑為
結論2棱長為a的正四面體的高為
結論3正四面體對棱中點的連線是對棱的公垂線.棱長為a的正四面體的對棱間的距離為.設正四面體兩個面的夾角為α,則.
結論1 和2 較容易證明,只證結論3.
證明如圖9, 設正四面體ABCD的棱BC,AD的中點分別為M,N.連接AM,DM, 易知AM=DM, 從而MN⊥AD.同理MN⊥BC, 故MN是BC和AD的公垂線.設正四面體ABCD棱長為a, 則,從而.易知AM⊥BC,DM⊥BC,從而∠AMD為二面角A-BC-D的平面角,故∠AMD=α,因此.
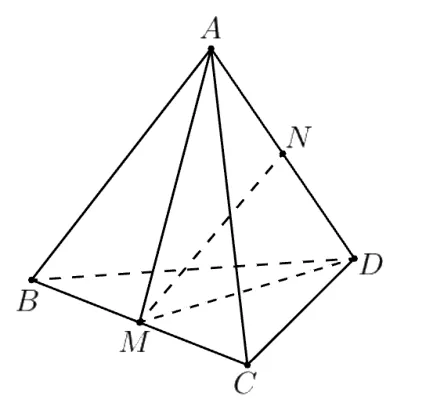
圖9
若圓柱的一個底面圓心和正四面體的一個面的中心重合,且圓柱的高垂直于這一個面,則稱這種方式為正接,如圖10 所示.
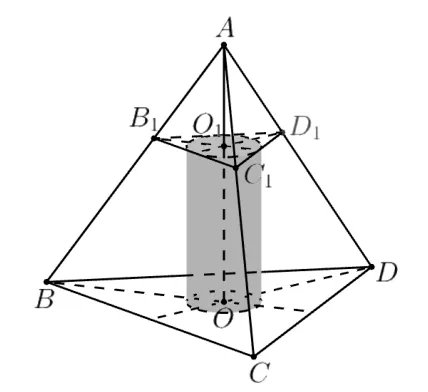
圖10
不妨設圓柱的底面圓心O與正四面體ABCD的面BCD的中心重合,另一個底面所在的平面與四面體三條棱AB,AC,AD的交點分別為B1,C1,D1, 則此底面的圓周恰好是?B1C1D1的內切圓.設AB1=B1C1=C1D1=D1B1=x(0 若圓柱底面圓心的連線與正四面體對棱的公垂線重合,則稱為斜接,如圖11 所示.不妨設圓柱底面圓心的連線與正四面體ABCD的對棱BC和AD的公垂線MN重合,其中M,N分別為BC和AD的中點. 圖11 設圓柱與面ABC的接觸點為P, 相應的底面圓心為O.根據對稱性可知點P在線段AM上.設OM=x, 則.由結論3 可知, 圓柱底面半徑, 圓柱高.故此時圓柱高與底面半徑的關系為.此時圓柱體積求導得,從而當時,V(x)單調遞增,當時,V(x)單調遞減.因此,斜接于正四面體的圓柱體積的最大值為 還有其它內接方式嗎?回答是: 還有.如圖12 所示,此時, 圓柱的側面與正四面體的兩個面相切, 我們稱這種內接方式為側接.如圖12,不妨設圓柱側面與面ABC和面ABD相切,AB中點為M,CD中點為N,圓柱底面與面ACD的接觸點為P, 與面ABC的接觸點為E, 相應的底面圓心為O,圓柱底面圓心連線與面ACD的交點為F.根據對稱性可知點P和點F在線段AN上.設直線OP與AB交于點Q,連接QE. 易知AB平行于圓柱母線, 故AB⊥PQ,AB⊥OE, 從而AB⊥QE, 故∠OQE為二面角C-AB-D的平面角的一半.設圓柱半徑為r, 根據結論3 可知.從而,故.易知?AQP與?AMN相似,從而,故 圖13 問題4什么樣的圓錐可以放入棱長為a的正四面體內? 也分為正接和斜接兩種情形.正接較容易解決, 如圖14 所示.此時圓錐底面半徑為, 高為, 體積為. 圖14 下面考慮斜接, 如圖15 所示.圖中字母的意義與圖11相同.設OM=x, 則, 圓錐底面半徑,圓錐高.故此時圓錐高與底面半徑的關系為. 圖15 此時圓錐體積 圖16 類似前面可知,斜接于正四面體的圓錐一定可以“正著”放入正四面體內. 也可考慮正四面體的側接圓錐,此時,圓錐底面半徑和高的關系為.限于篇幅,不再展開討論. 原題是一道別具一格的優秀試題,雖然其中的D 選項可借助幾何直觀進行“秒殺”,但數學是嚴謹的演繹科學,作為數學教育工作者,理應弄清楚“將0.01m 的厚度忽略”的底層邏輯.這樣,面對學生刨根問底的提問時,才能做到“心中有數,手中有法”,不至于亂了陣腳.一道優秀試題往往有著旺盛的生命力和深入挖掘的價值, 本文嚴謹地解決原試題后,將其作了進一步的引申和類比,得到了正方體和正四面體內接圓柱和圓錐的底面半徑和高之間的精確關系.據此可以編制出一些變式問題,茲舉例如下. 變式下列物體中,能夠被整體放入棱長為1(單位: m)的正四面體容器(容器壁厚度忽略不計)內的有( ) A.直徑為0.4m 的球體 B.底面邊長為0.5m,高為0.4m 的正三棱柱 C.底面直徑為0.01m,高為1.1m 的圓柱體 D.底面直徑為0.25m,高為0.45m 的圓柱體 解析設棱長為1m 的正四面體為ABCD,設其各面的面積為S,高為h,內切球半徑為r. 對于B 選項,設棱AB,AC,AD的中點分別為B1,C1,D1,考慮以?B1C1D1為底面,另一底面落在面BCD上的正三棱柱, 如圖17 所示.易知, 此正三棱柱的底面邊長為0.5m,高為,故底面邊長為0.5m,高為0.4m 的正三棱柱可以放入棱長為1m 的正四面體內,B正確. 圖17 對于C 選項,正四面體內任意兩點的距離不可能超過正四面體的棱長,故高為1.1m 的圓柱體不能放入棱長為1m 的正四面體內,C 不正確. 對于D 選項, 根據本文第四節所得的正接于正四面體的圓柱的底面半徑與高之間的關系, 可知當圓柱底面直徑為0.25m 時, 高為,故底面直徑為0.25m,高為0.45m 的圓柱體以放入棱長為1m 的正四面體內,D 正確.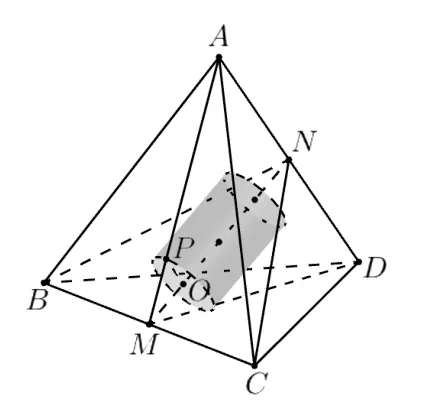

5 什么樣的圓錐可以放入正四面體內?


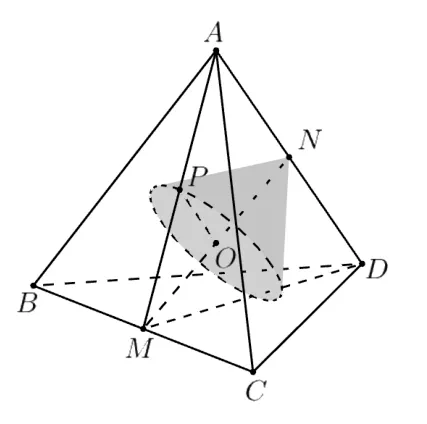
6 寫在最后