永磁直線同步電機自適應反推非奇異終端滑模控制
張 悅,趙希梅
(沈陽工業大學 電氣工程學院,沈陽 110870)
0 引 言
永磁直線電機省去了中間機械傳動環節,以其結構簡單、可靠性高、定位精度高、響應速度快等優點,適用于高速高精度要求的場合,廣泛應用于高檔數控機床、半導體制造、工業機器人等各類精密加工領域[1]。但直接驅動方式也導致了各種擾動將直接作用在電機動子上,限制了系統位置跟蹤精度的提高[2]。因此,快速準確的擾動抑制是實現動子高精度跟蹤的關鍵所在,這就對控制系統設計提出了苛刻要求。
眾所周知,滑模控制(以下簡稱SMC)具有設計簡便、控制效果好、魯棒性強等優點,在電機控制領域得到了廣泛應用。傳統SMC采用線性滑模面,其跟蹤誤差的收斂時間無窮大;另外由于系統固有延遲及慣性問題的影響,系統狀態軌跡會在滑模面附近頻繁切換,產生高頻抖振,增加系統的電損耗和機械損耗,因此難以滿足高性能場合下的控制要求。而引入非線性項的終端SMC,可以使得被控狀態在有限時間內收斂,成為了該領域的研究熱點[3]。文獻[4]提出了非奇異快速終端SMC方法,避免了普通終端滑模中控制量無窮大的問題,并使其在系統狀態遠離平衡點的位置也能得到較快的收斂,但外部擾動出現時系統不穩定。文獻[5]在非奇異快速終端滑模中引入自適應控制算法,對系統的不確定性上界進行自適應補償,減小了滑模切換增益,削弱了抖振現象,提高了系統魯棒性。
近年來,反推控制得到了廣泛關注,作為一種非線性系統控制策略,運用遞歸的思想,先引入虛擬控制輸入項,將系統分解為低階子系統,同時選擇合適的Lyapunov函數,在保證各子系統的穩定性的同時,實現對系統的全局調節[6]。文獻[7]提出了反推全局快速終端滑模控制的方法,將反推與SMC相結合,先對復雜系統進行分解,再利用全局快速終端SMC,使得系統在平衡點附近也能夠實現快速收斂。但其控制器中指數項是負數,使系統控制量可能會趨于無窮大,進而產生奇異現象。文獻[8]在全局積分終端滑模的基礎上,引入RBF徑向基神經網絡擾動觀測器,進一步減小切換增益,削弱抖振。針對擾動問題,文獻[9]通過非奇異快速終端SMC方法實現了永磁直線電機位置跟蹤誤差的快速收斂,并將系統集總擾動通過高階超螺旋擾動觀測器反饋給滑模控制器,減小了系統的抖振現象。其中非線性擾動觀測器由于其計算簡單,且能做到對非線性系統狀態的全部觀測,獲得了廣泛應用[10-11]。文獻[12]針對系統外部干擾,采用非線性擾動觀測器(以下簡稱NDO)進行實時辨識并補償,提高了系統的跟蹤精度和抗干擾能力。
本文提出基于NDO的自適應反推非奇異終端滑模控制(以下簡稱NDO-ABNTSMC)方法,將NDO與反推非奇異終端滑模控制(以下簡稱BNTSMC)相結合,首先通過反推控制將系統降階處理,再利用BNTSMC實現系統有限時間內的快速收斂,并利用自適應控制適時調整滑模控制器切換項,削弱滑模抖振。然后采用NDO觀測系統的集總擾動,并前饋補償給滑模位置控制器,以提高系統的魯棒性。最后,通過仿真對本控制方法的有效性進行了驗證。
1 數學模型
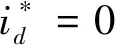
(1)
式中:ud、uq、id、iq、Ld、Lq分別為d、q軸的電壓、電流和電感;Rs為電樞電阻;ψPM為永磁體磁鏈;p為極對數;x2為直線電機動子速度;τ為極距。
電機電磁推力可表示:
(2)
(3)
式中:Kf為電磁推力系數。PMLSM動力學方程可表示:
(4)
式中:M為PMLSM的動子質量;B為粘滯摩擦系數;Γ表示系統集總不確定擾動,包括參數變化、負載擾動、非線性摩擦力、端部效應及齒槽效應等。
2 PMLSM控制系統設計
2.1 反推非奇異終端滑模控制器設計
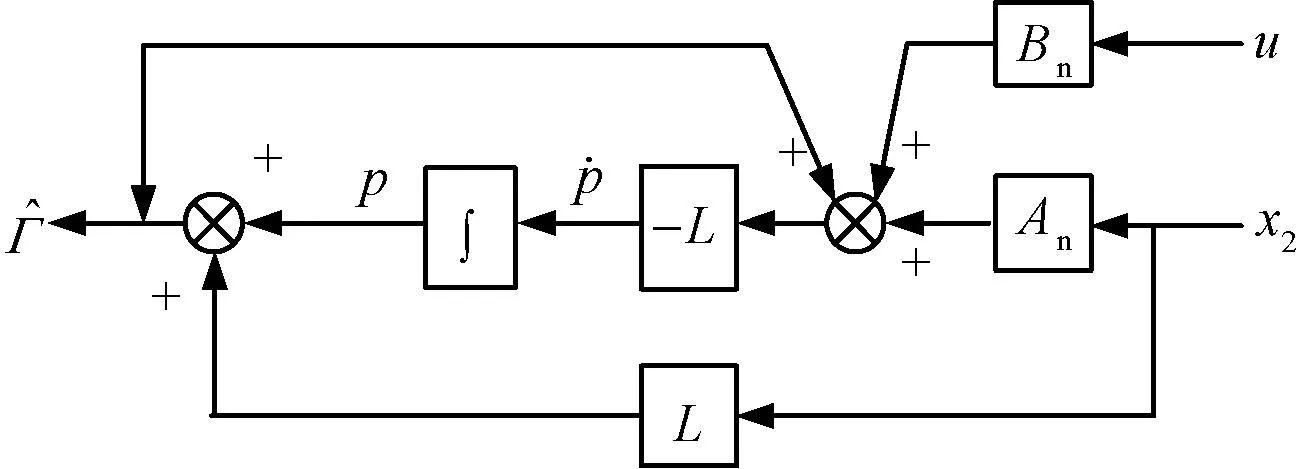
PMLSM實現高精度位置跟蹤的控制,要求在擾動情況下,電機動子仍可以準確跟蹤給定參考軌跡。因此,本文利用非奇異終端滑模的快速收斂性,再結合反推算法,逐步推導出實際的控制律,實現對系統的全局控制,基于NDO-ABNTSMC的PMLSM系統控制框圖如圖1所示。
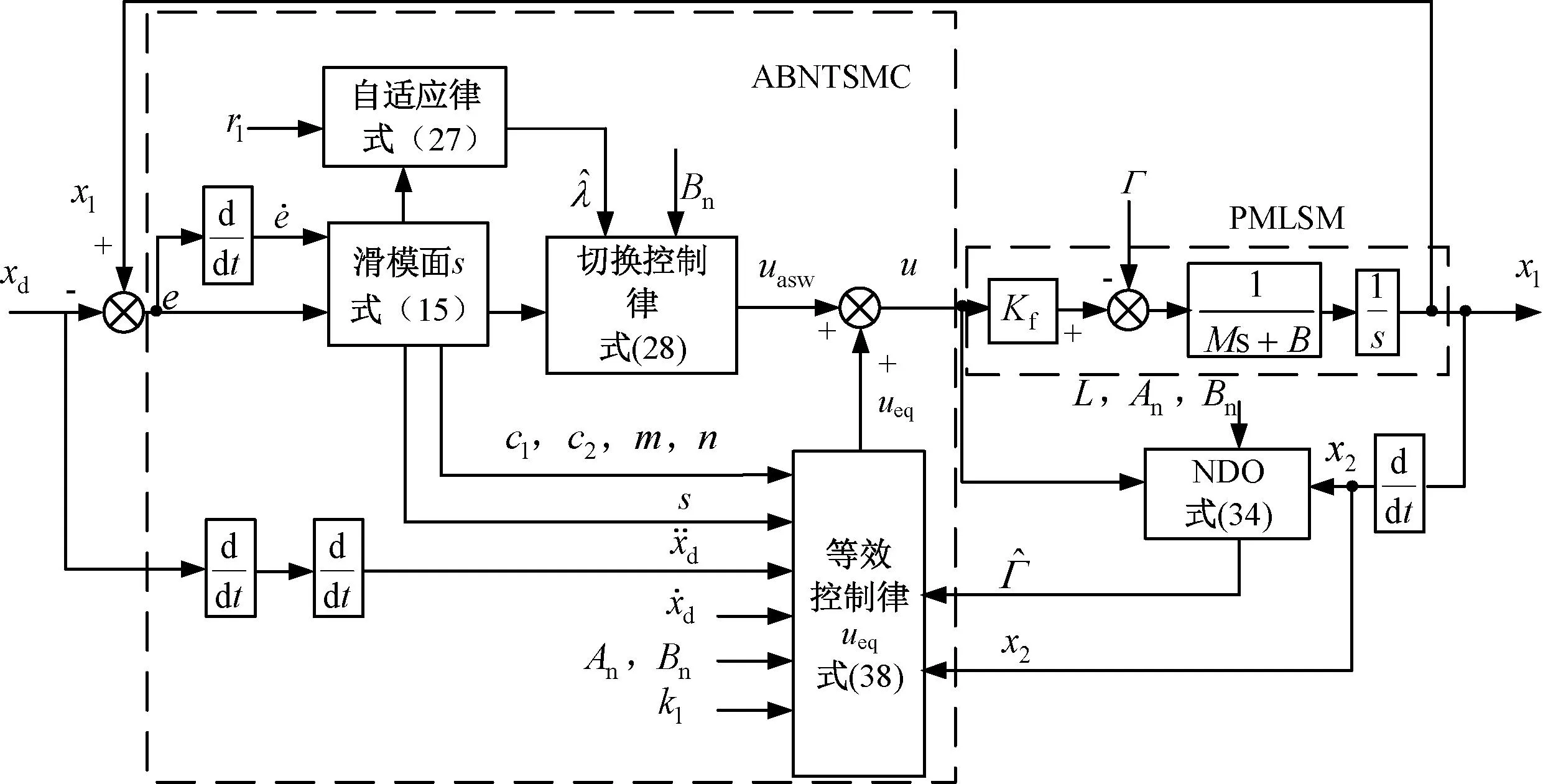
圖1 基于NDO-ABNTSMC的PMLSM系統控制結構框圖
首先,定義位置跟蹤誤差:
e=x1-xd
(5)
式中:xd為給定參考位置;x1為動子的實際位置。
(6)
式中:x2為動子的實際速度。
定義穩定函數:
α1=-k1e+s
(7)
式中:k1>0;s為滑模面。
為保證穩定性,構造第一個Lyapunov函數:
(8)
求導可得:
(9)
其次,定義虛擬控制輸入:
(10)
(11)
則:
(12)
將式(11)代入式(9)中可得:
(13)
當s→0時,有:
(14)
由Lyapunov定理可知,當s→0時,位置跟蹤誤差e漸進穩定。
接著,選定非奇異終端滑模面:
(15)
式中:設計參數c1,c2>0;m,n為正奇數,且滿足1 (16) 為證明穩定性并保證系統狀態變量始終保持在滑模面s上,構造第二個Lyapunov函數: (17) 求導可得: (18) 代入式(11)和式(12),可整理得: (19) (20) 另外,選擇切換控制律: (21) 式中:δ,η>0,為待設計的控制參數,其中η為一較小值,δ為切換增益,且滿足系統集總擾動|Γ|≤δ,通過選擇合適的δ值,可以削弱滑模抖振現象。 由此,系統總的控制律: (22) 將式(22)代入式(19)得: (23) 實際仿真過程中,集總擾動Γ的上界是很難獲得的,通常采用試湊法來選定切換增益δ的值,而切換增益過大會加劇系統抖振,過小則會降低系統的抗擾能力。為此,本文在BNTSMC中引入自適應控制方法,自適應調整切換增益,從而對系統抖振與抗擾效果進行折衷考慮。 令λ=δ+η,則估計誤差: (24) (25) 對V3求導,并結合式(23)和式(24)得: (26) (27) 此時,自適應切換控制律表示: (28) 將式(27)代入式(26)可得到: (29) 由Lyapunov第二方法可知,此時系統漸進穩定。 采用NDO對集總擾動Γ進行估計補償,來進一步提高系統的魯棒性。NDO主要通過觀測器估計值與實際輸出之間的差值來對估計值進行調整,其控制結構框圖如圖2所示。 圖2 NDO結構框圖 系統的集總擾動: (30) 引入觀測器增益L,則NDO設計: (31) 定義輔助變量對式(31)進行降階處理,即: (32) 對式(32)求導可得: (33) 即整理得到如下的NDO: (34) 定義NDO的跟蹤誤差: (35) 求導得: (36) (37) 引入非線性擾動觀測器后,可對集總擾動Γ進行觀測,因此系統的控制律中無需再忽略集總擾動項,此時系統等效控制律表示: (38) 代入式(28)和式(38),系統總的控制律由式(22)變為: (39) (40) (41) (42) (43) 對式(43)兩端同時積分,可得: (44) 因此,當t≥0時,Lyapunov函數非增且有界。又因為e、s有界,當t→∞時,則有: (45) 由Barbalat引理,k1e2+λ|s|有界,因此有 (46) 可推出s和e漸進收斂,因此基于NDO的ABNTSMC方法可以使系統漸近穩定,保證系統位置跟蹤誤差在有限時間內衰減為零。 PMLSM的主要參數:Rs=2.1 Ω,Ld=Lq=41.4 mH,ψPM=0.09 Wb,τ=32 mm,M=16.4 kg,Kf=50.7 N/A,B=8.0 N·s/m。 其中SMC控制器參數:c=18,δ=18,η=0.1;ABNTSMC控制器參數:c1=200,c2=10,m=5,n=3,k1=5,r1=1 200;NDO-ABNTSMC控制器參數:c1=90,c2=1,m=5,n=3,k1=5,r1=1 200,L=2 000。 首先,驗證NDO的擾動觀測能力,為便于分析,忽略電機內部參數的變化,而只改變電機的外加負載情況,施加如圖3所示的突加負載。可以看出,0.5 s時負載由零突變為30 N,NDO可以較好地觀測負載變化,在4 ms內逐漸逼近真實值,且幾乎無波動。由此可見,本文所設計的NDO具備較高的觀測速度與觀測精度。 圖3 突加負載實際值與觀測值曲線 為驗證有效性,分別對SMC、ABNTSMC、NDO-ABNTSMC三種方法控制的PMLSM伺服系統在不同工況下進行對比。 1)驗證本方法在階躍信號下的響應性能。 系統空載起動,跟蹤幅值為1 mm的階躍信號,并在0.8 s時刻突加100 N的負載擾動,觀察系統的響應情況。三種控制方法的位置響應曲線如圖4所示。 由圖4可以看出,隨著電機空載起動,SMC方法緩慢跟蹤給定信號,并在突加100 N負載時,立即偏離跟蹤信號,穩定后始終維持著平均25 μm左右的穩態誤差;而ABNTSMC和NDO-ABNTSMC方法具有更快的響應速度,電機空載起動后大約0.05 s到達了期望軌跡,其中ABNTSMC方法下系統在起動期間有約20%的超調量,在0.8 s突加負載后產生較大的偏移量,雖然在約0.6 s時可收斂至跟蹤信號,但其突加負載瞬間產生誤差較大,可達到0.13 mm,且收斂緩慢;而基于NDO-ABNTSMC方法在電機起動期間避免了超調現象,在突加負載時的瞬間誤差非常小,只有5.6 μm,且收斂速度非常快,約0.05 s后即收斂到給定值附近。由此可見,相較于另外兩種方法,基于NDO-ABNTSMC方法通過NDO觀測負載擾動并進行前饋補償,使得階躍信號跟蹤下,系統具有更快的響應響應速度和更強的抗擾能力。 2)驗證周期性正弦信號下,本方法的響應性能。 對系統給定如圖5所示的幅值30 mm、周期為2 s的正弦位置信號,在標稱狀態下和電機參數變化(粘滯摩擦系數B變為2倍)的情況下,三種控制方法下系統的位置響應誤差曲線分別如圖6和圖7所示。 圖5 給定正弦信號 圖7 正弦信號下系統的響應性能曲線(參數變化) 由圖6可以看出,在標稱狀態下三種方法對正弦位置信號都有著不錯的跟蹤效果,在給定信號隨著時間發生變化時,均能夠緊密地跟蹤給定信號。SMC下系統跟蹤誤差跟隨給定信號產生較大的上下波動,誤差約在±5 μm之間。與之相比,ABNTSMC下,位置誤差的波動范圍明顯減小,在±3 μm左右。而NDO-ABNTSMC方法對系統的控制方法進一步優化,具有最小的位置跟蹤誤差,誤差波形約在-1.5 μm~1.5 μm的范圍內隨著給定信號小幅度上下波動,與前兩種控制方法相比,位置誤差波動范圍分別減小了70%和50%。可見,NDO-ABNTSMC方法可以較好地抑制擾動,誤差波動更小,系統位置跟蹤效果更好。 如圖7所示,當系統參數發生變化時,三種控制方法下伺服系統仍有著不錯的位置響應性能,只是跟蹤誤差的波動范圍均有所擴大。在參數變化的情況下,SMC和ABNTSMC方法下系統的位置誤差范圍分別擴大到±10 μm和±8 μm之間。而相較之下,NDO-ABNTSMC方法由于非線性擾動觀測器的加入,電機參數的變化得以被觀測和補償,因此與ABNTSMC相比,系統的抖振明顯減小,同時位置跟蹤誤差也最小,僅在約±2 μm的范圍內隨著給定正弦信號小幅度波動。因此,NDO-ABNTSMC方法能夠較好地克服參數變化對系統的影響,可以較好的提高系統的抗擾能力和位置跟蹤精度。 為提高系統位置響應性能,本文提出了一種基于NDO的ABNTSMC方法,并在PMLSM的數學模型基礎上,對控制算法的有效性進行仿真驗證。由上述結果可以看出: 1)本文將反推與非奇異終端SMC相結合,提高了系統魯棒性,保證了系統響應的快速性,且避免了奇異問題。同時結合自適應算法,動態調整滑模切換增益,削弱了滑模抖振; 2)引入的NDO實現了對負載擾動的觀測與補償,提高了系統抗擾能力,進一步提高了系統位置跟蹤性能; 3)在負載擾動和參數變化條件下,基于NDO的ABNTSMC方法可以對擾動進行有效識別,系統響應更快誤差更小,抖振現象減弱,具有強魯棒性。
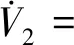
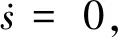
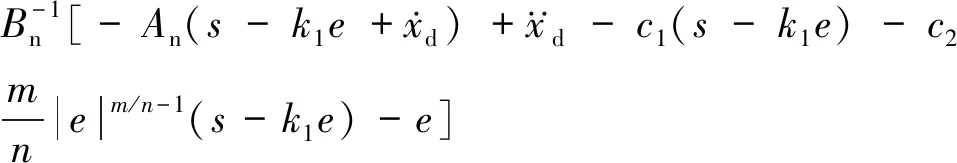
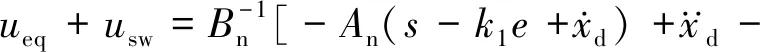
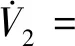
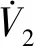
2.2 自適應反推非奇異終端滑模控制器設計
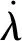
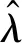
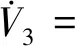
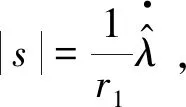
2.3 NDO的設計

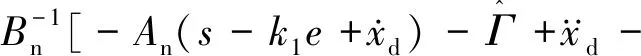
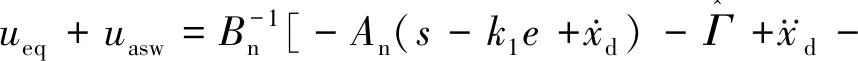
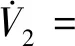
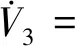
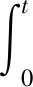
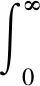
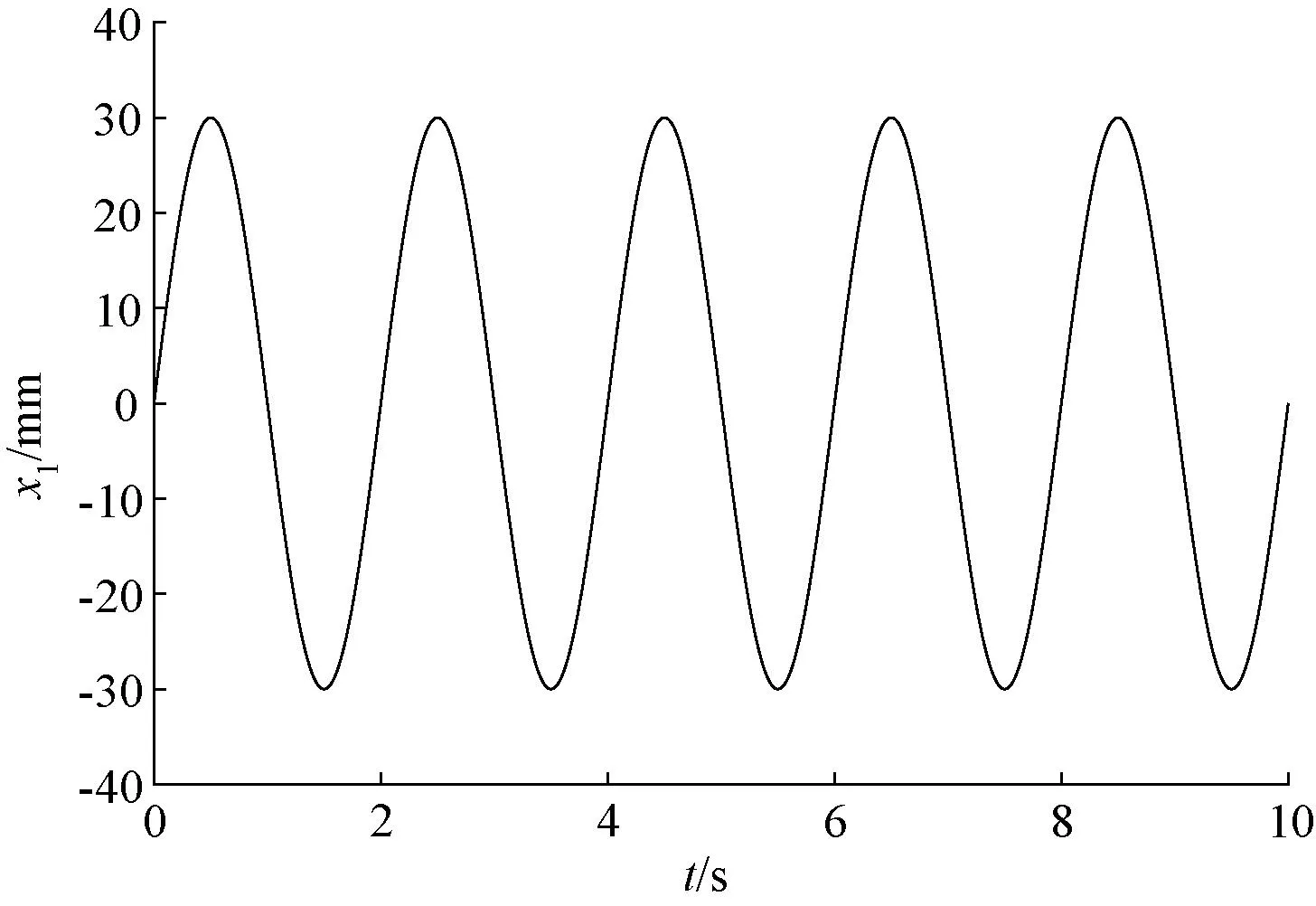
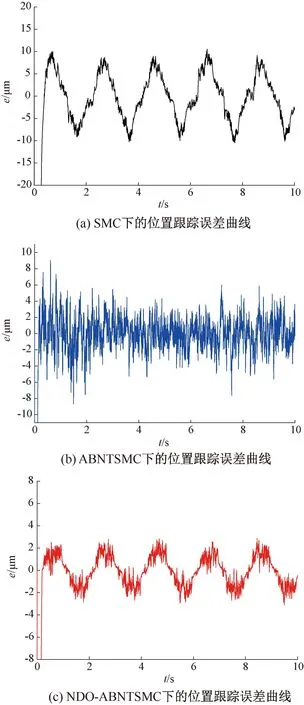
3 系統仿真結果及其分析

4 結 語

