環形流道內擾流柱參數優化的模擬分析

王風錄 虞 斌 呂 林 許 蕾

（南京工業大學機械與動力工程學院）

套管式熱交換器［1］被廣泛應用于石油、化工等行業的生產過程中。 相較于其他形式的換熱器，套管式熱交換器具有結構簡單、換熱面積增減自如、傳熱效能高及純逆流傳熱等優點。 在設計過程中基于傳熱介質物性的不同，可使用多種被動方式提高套管結構的傳熱效率，如改變套管的形 狀［2，3］，加裝 翅片［4～7］、肋槽［8，9］、擾流 柱［10～12］及內插物［13，14］等，通過破壞或消除流體壁面 的邊界層、產生二次流促進流體的混合、改變流場和溫度場的分布特性以及增大換熱面積等方式，達到強化換熱的效果。

張延靜等指出，釘頭管換熱器具有良好的強化傳熱效果，與光管相比，其總傳熱系數可提高約88%［15］。釘頭結構既增大了傳熱面積，也使套管環形流道中的流體更易形成湍流，能夠進一步強化換熱。 ZHANG L等指出，安裝擾流柱的螺旋流道具有更高的流速，速度分量的功率譜范圍也更寬［16］，擾流柱能夠顯著增加湍流的生成。 虞斌等研究的一套高溫高含塵爐氣急冷器系統中采用了套管結構［17］。設備中的套管結構可將1 500 ℃的高溫爐氣在極短時間 （0.01 s） 內急速冷卻到750～900 ℃，過程中可獲取大量熱能。 在內、外套管之間須設置支撐結構， 保證總長度約12.5 m的內管在壓力和溫度的作用下，具有足夠的剛度，不致發生屈曲失效等；同時，套管間的支撐結構也能夠起到強化傳熱的效果。 筆者在之前的研究基礎上， 在套管的環形流道內周期性地布置不同參數的擾流柱， 并采用正交試驗結合數值模擬的方法對其進行優化，使之獲得更好的強化傳熱效果。

1 模型描述

1.1 模型建立與基本假設

高溫高塵爐氣急冷器的結構如圖1所示，中段部分為套管結構，取該部分作為研究對象。 套管的內外管長度均為7.5 m，外管尺寸為φ89 mm×6 mm，內管尺寸為φ62 mm×5 mm；擾流柱的截面為橢圓形，短軸長度為a，長軸長度為b，扭轉角為α，相鄰兩環擾流柱的圓周差角為β，擾流柱數量為每環m個，如圖2所示。為得到更好的模擬結果，在套管的出入口處均同時延長一段距離。 套管內管中的介質為高溫煙氣，密度0.474 kg/m3［18］；環形流道中的介質為軟水，密度951 kg/m3。 套管材料為15CrMo。

圖2 套管和擾流柱局部結構示意圖

對模型的數值計算做如下假設：

a.物理模型為三維結構，最外層壁面不與環境發生熱交換；

b.忽略重力對流場的影響；

c.流體為不可壓縮流體，是穩態的、充分發展的湍流。

1.2 邊界條件與數值處理方法

邊界條件：內管的進口為速度入口62 m/s，溫度1 500 ℃； 環形流道的進口為速度入口0.6 m/s，溫度110 ℃； 內管與環形流道的出口均采用壓力出口，分別為0.3、4.0 MPa。 所有壁面均采用無滑移邊界條件；固-液交界壁面設置為耦合壁面；最外側壁面采用絕熱壁面， 不與外界發生熱量交換。

數值處理方法：

a.采用雙精度求解器， 選取RNG k-ε方程模型，并對壁面采用增強壁面函數處理；

b.由于內管介質是高溫煙氣，套管的換熱除了對流傳熱外， 還必須考慮煙氣的輻射換熱，因此激活P-1輻射模型；

c.壓力和速度耦合采用Simple算法，動量、能量、湍動能和湍流耗散率離散均采用二階迎風格式，以提高精度。

2 正交試驗及分析

2.1 評價指標

努塞爾數Nu和阻力系數f的定義如下：

式中 de——當量直徑；

h——對流換熱系數；

L——有效長度；

u——流場平均流速；

ΔP——進出口壓降。

為了評價環形流道內設置不同尺寸參數擾流柱的綜合強化傳熱性能，引入工程上普遍使用的綜合評價指標（PEC），其計算式為：

式中 f——有擾流柱的套管的阻力系數；

f0——無擾流柱的套管的阻力系數；

Nu——有擾流柱的套管的努塞爾數；

Nu0——無擾流柱的套管的努塞爾數。

2.2 正交試驗

正交試驗可以在短時間內用較少的試驗次數確定不同因素的最佳匹配關系。 模擬因素包括擾流柱橢圓截面的短軸長度a、長短軸之比c、擾流柱的環向布置個數m、軸向布置環數n、相鄰兩環的圓周差角β和擾流柱的扭轉角α，共6個因素，目標函數是Nu、f和PEC。 在不考慮交互作用的情況下，本次研究使用正交表L18（36）。

2.3 網格無關性驗證

對模型進行網格無關性計算分析，選取正交試驗中第2組試驗， 以環形流道的壓降作為觀測變量，其網格無關性分析規律如圖3所示。 網格數量達到60萬之后，壓降變化趨于平緩，故選取70～80萬網格作為計算網格。

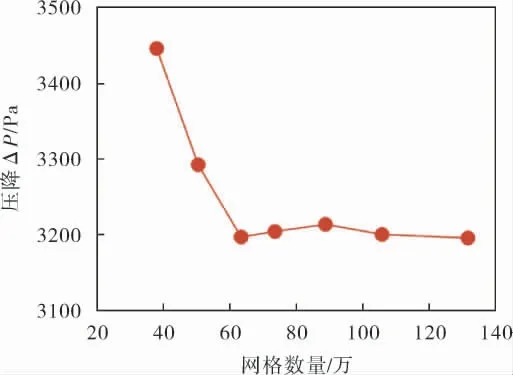
圖3 計算網格獨立性驗證

2.4 試驗結果與極差分析

正交試驗選取的因素、水平、方案和計算結果見表1。采用極差分析法對結果進行分析。極差分析法是計算相同試驗因素在不同水平下的平均值，通過一組平均值中的極大值與極小值之間差值的大小，可以直觀地表現出各個因素影響目標函數的影響程度。 差值越大，說明該因素對目標函數的影響程度越大。

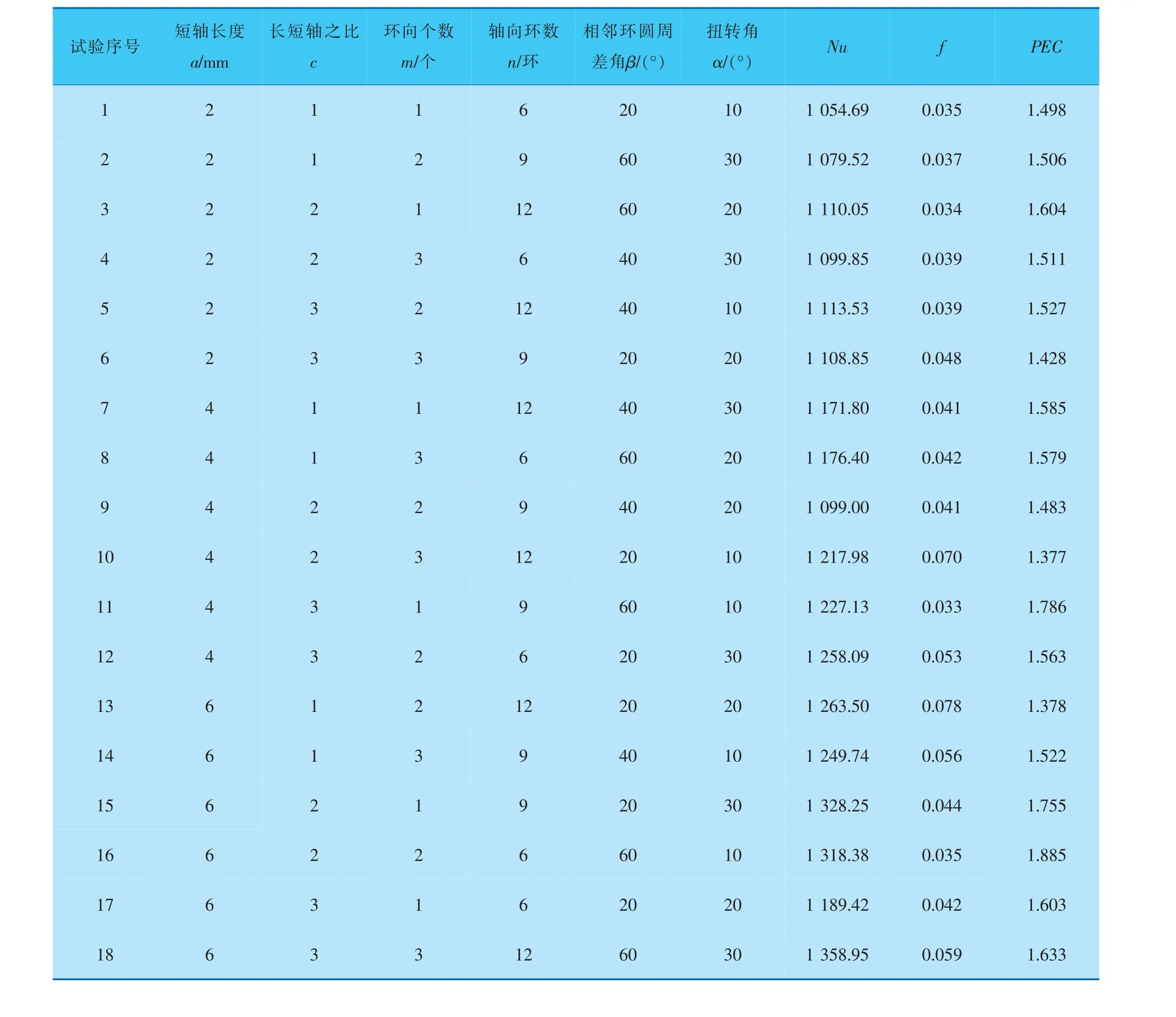
表1 擾流柱正交試驗表及數值計算結果

基于正交試驗結果分別對目標函數Nu、f和PEC進行極差分析。

基于極差分析結果得到各因素水平對Nu、f和PEC的影響趨勢如圖4所示。

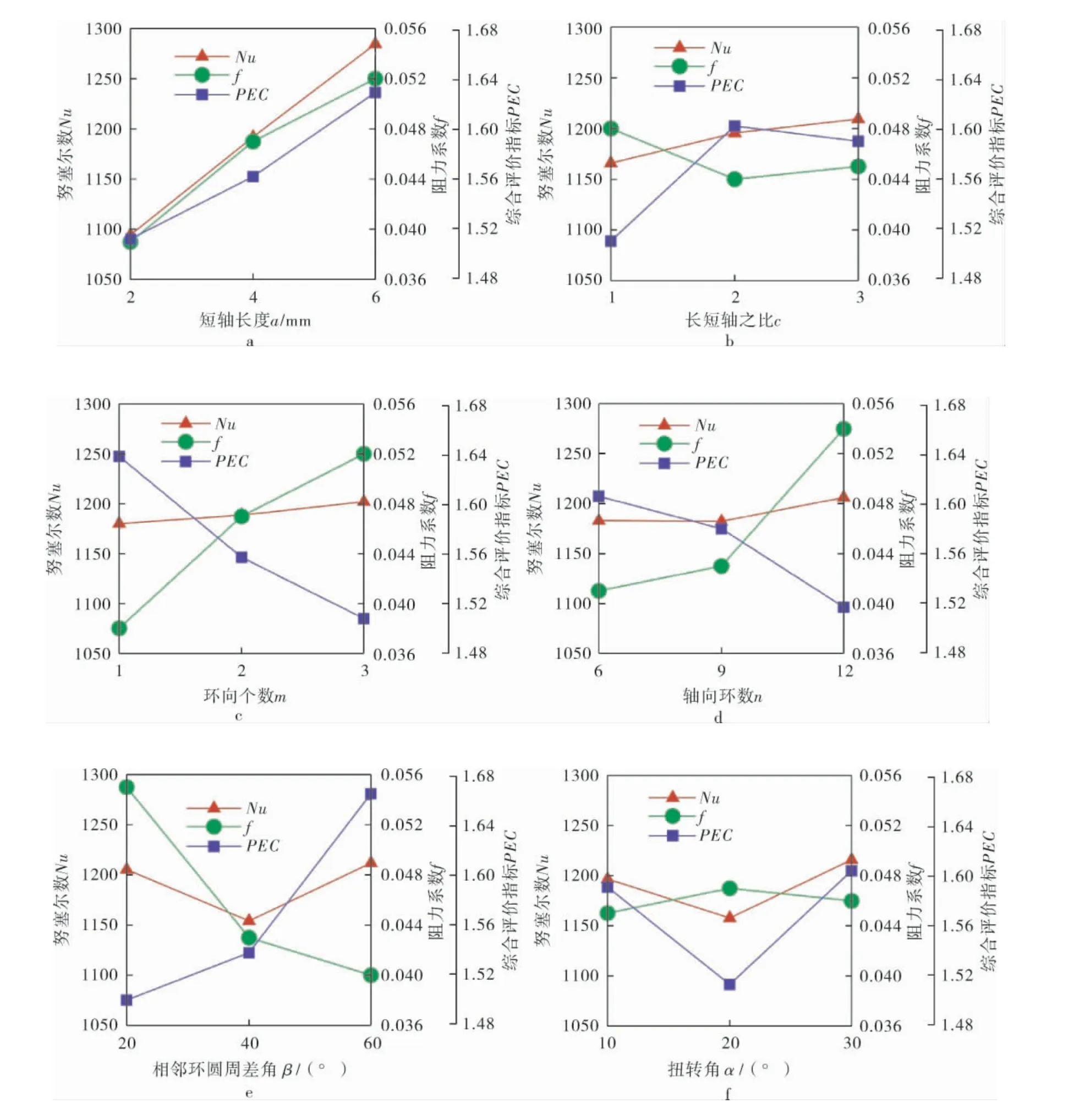
圖4 各因素水平對Nu、f和PEC的影響趨勢

因素水平對Nu的影響見表2，分析表2中的數據可知， 各因素水平對Nu影響的主次順序為：擾流柱的短軸長度a>扭轉角α>相鄰環圓周差角β>長短軸之比c>軸向環數n>環向個數m。 圖4中，隨著擾流柱短軸長度的增加，Nu顯著上升。 Nu對于長短軸之比、 環向個數和軸向環數3個因素的水平變化相對不敏感。 相鄰環圓周差角和扭轉角對Nu的影響受到多因素耦合作用，變化規律并不是隨著水平變化而單純的增加或減少。若只考慮Nu這一個指標， 最優的水平組合是A3B3C3D3E3F3，即為正交試驗中的第18 組試驗， 此時PEC 值為1.633。

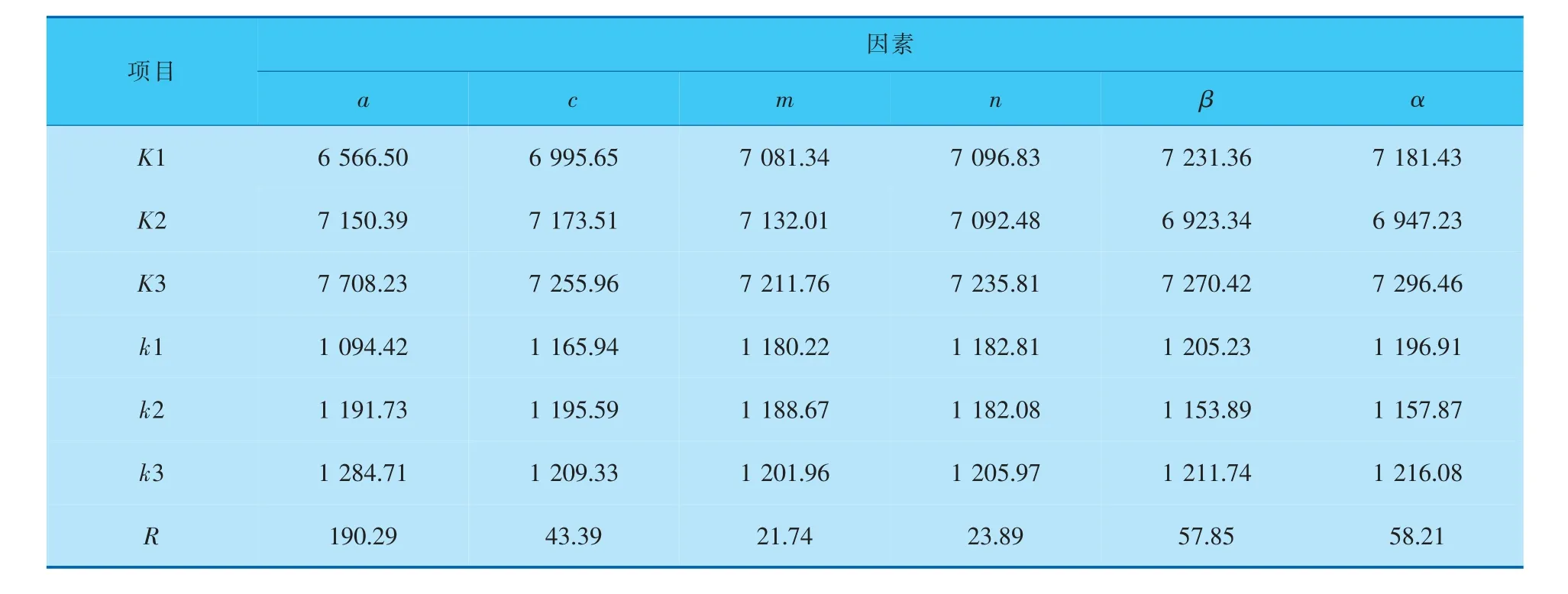
表2 Nu極差分析表

因素水平對阻力系數f的影響見表3，分析表3中的數據可知， 各因素水平對f影響的主次順序為：擾流柱相鄰環圓周差角β>環向個數m>短軸長度a>軸向環數n>長短軸之比c>扭轉角α。 圖4中，f隨著短軸長度的增加、環向個數和軸向環數的增多顯著上升； 相鄰環圓周差角的增加使f顯著下降。f對于長短軸之比和扭轉角的水平變化相對不敏感。 若只考慮f這一個指標，最優的水平組合為A1B2C1D1E3F1，經再次建模并數值模擬驗證其PEC值為1.50。

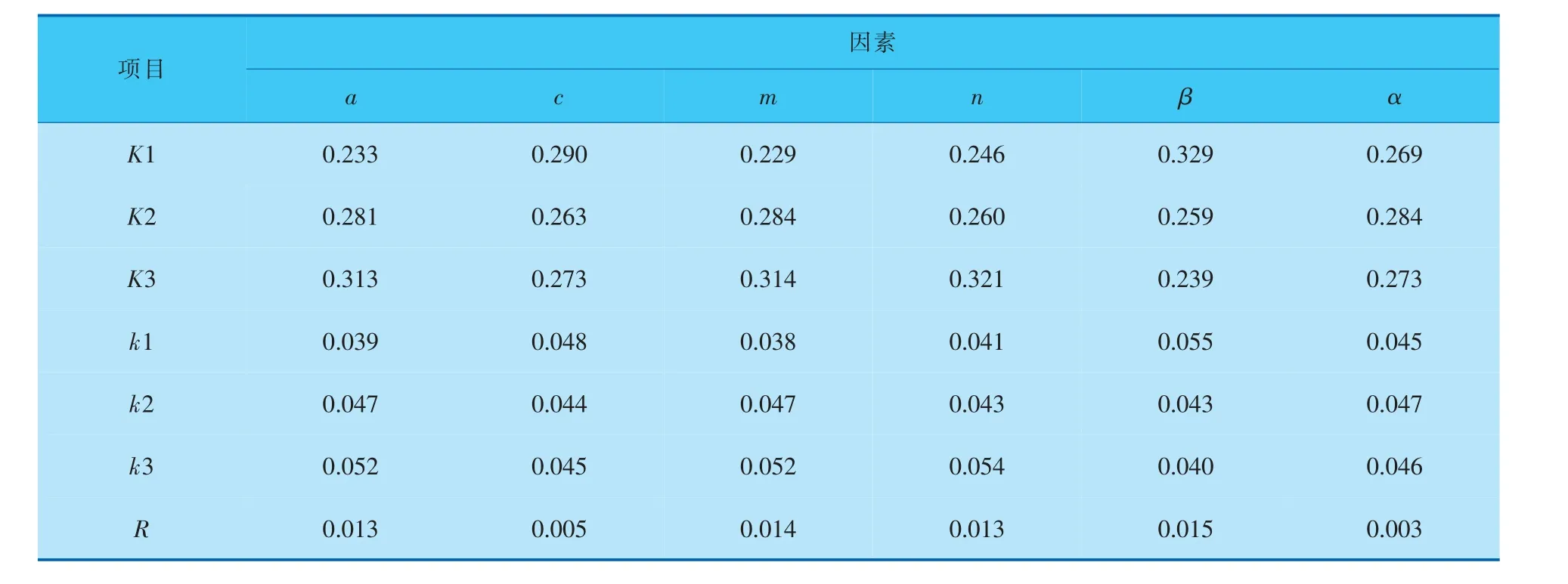
表3 f極差分析表

因素水平對PEC的影響見表4，各因素水平對PEC影響的主次順序為： 擾流柱的相鄰環圓周差角β>環向個數m>短軸長度a>扭轉角α>長短軸之比c>軸向環數n。 圖4中，擾流柱的相鄰環圓周差角β的增大會大幅降低流動阻力而使PEC顯著提高。 環形流道內的換熱面積隨著短軸長度的增加而增大，同時流場的壓降也會相應增大，使Nu、f和PEC同時顯著提高。 擾流柱環向個數和軸向環數的增加，僅會使Nu小幅度提升，但會大幅增加f，使得PEC大幅下降。 當擾流柱的長短軸之比大于1， 即采用橢圓形擾流柱對環形流道進行傳熱強化時，流場中的Nu、f和PEC均優于圓形擾流柱。此時優化組合方案是A3B2C1D1E3F3，即短軸長度為6 mm、長短軸之比為2、環向個數為1、軸向環數為6、相鄰環圓周差角為60°、扭轉角為30°。經數值模擬驗證其Nu為1 341.46，f為0.032，PEC為1.973。

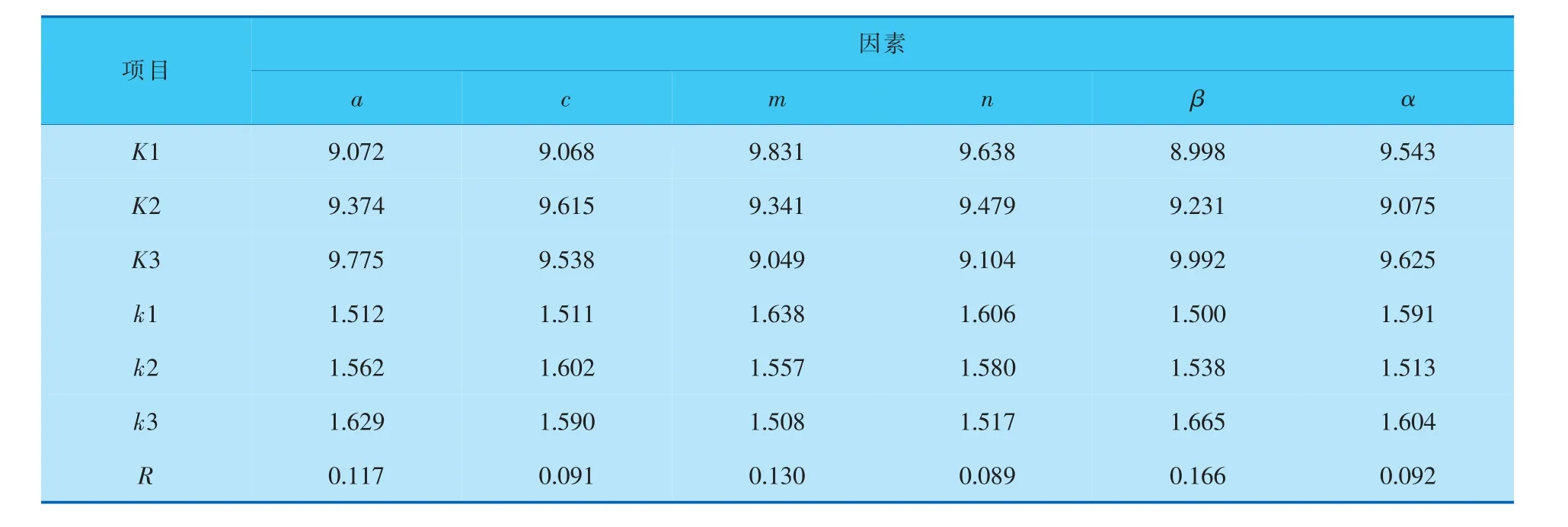
表4 PEC極差分析表

3 場協同分析

場協同原理［19］認為，對流換熱的性能不僅取決于流體的速度、 物性和流體與壁面的溫差，還取決于流體的速度場和溫度場之間的協同程度。在相同的速度和溫度邊界條件下，速度場與溫度場之間的協同程度越好，換熱強度就越高。

管內對流換熱的溫降主要發生在徑向，其徑向溫度梯度遠大于軸向溫度梯度， 一般徑向溫度梯度比軸向溫度梯度大2～3個數量級甚至更多［20］。對于套管的環形流道內的溫度場也具有相同規律。 因此，只要提高流體徑向速度，即可對換熱產生顯著的影響。 圖5是光管和PEC=1.973組合的套管環形流道內的徑向速度和軸向速度絕對值之比沿徑向方向的變化。 相較于光管，環形流道內設置的具有扭轉角的橢圓形擾流柱使徑向速度大幅提升，約可達到軸向流速的4%。

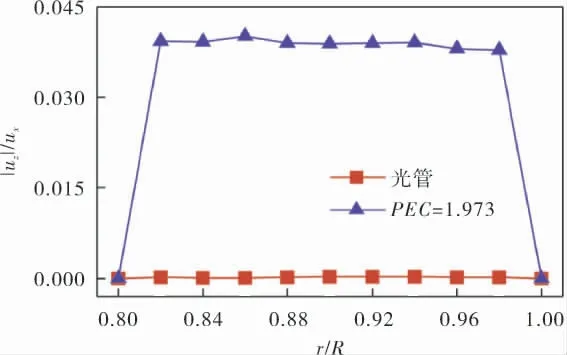
圖5 徑向速度和軸向速度絕對值之比沿徑向方向的變化

取r/R=0.90處的柱面溫度云圖并沿圓柱母線展開，如圖6所示。 可以看到具有擾流結構的環形流道內的溫度場分布更均勻。 這種強化措施顯著改善了流道內的場協同效果，起到了強化傳熱的作用。

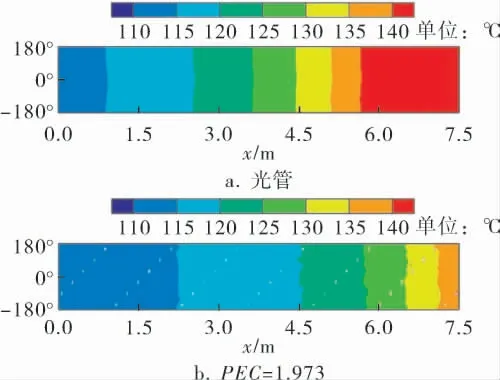
圖6 r/R=0.90處的溫度場圓周展開示意圖

4 結論

4.1 基于數值模擬和正交試驗結果對綜合評價指標PEC進行極差分析， 套管中安裝具有扭轉角的橢圓形擾流柱的結構參數中，擾流柱的相鄰環圓周差角對其流動特性和傳熱性能綜合影響最大，并得出一組綜合換熱效果最優的結構參數組合，其PEC=1.973。

4.2 基于場協同理論分析，環形流道內設置的具有扭轉角的橢圓形擾流柱使徑向速度大幅提升，約可達到軸向流速的4%。這種強化措施顯著改善了流道內的場協同效果，起到了強化傳熱的作用。