壓裂液黏度和注液速率對含層理頁巖水力裂縫擴展行為的影響規律研究
白岳松 ,胡耀青 ,李 杰
(1.太原理工大學 礦業工程學院,山西 太原 030024;2.中煤科工集團沈陽研究院有限公司,遼寧 撫順 113122;3.煤礦安全技術國家重點實驗室,遼寧 撫順 113122)
我國頁巖氣資源豐富,但是頁巖氣儲層同時存在滲透性差、開采難度高等特點[1-5]。為此,眾多學者為有效提高頁巖氣儲層的滲透性而進行研究并提出多種開采技術。其中,水力壓裂技術為應用最為廣泛的技術[6-12]。為了優化水力壓裂技術對頁巖氣儲層滲透性的改造,有必要探究在對頁巖氣井進行水力壓裂過程時影響其裂縫擴展的影響因素,特別是頁巖氣儲層中含有層理構造時其水力裂縫擴展行為的影響因素。KAHRAMAN S等[13]采用巖石脆塑性及斷裂韌性等參數對儲層的可壓裂性進行評價;趙爭光等[14]采用地面微震技術證實儲層的巖性是影響其水力裂縫擴展的重要因素;劉建中等[15]采用物理模擬實驗的方法發現水力裂縫在壓裂后的延伸過程中會逐漸沿著垂直于最小水平主應力的方向擴展;門曉溪[16]通過數值模擬發現儲層中的層理角越大,其起裂壓力越大;李曉等[17]采用實驗室試驗的方法,得到層理傾角小于30°時頁巖破裂所需破裂壓力大,且破壞形態差異大的試驗結果;HENG S 等[18]通過試驗發現,在水力壓裂過程中當水力裂縫和層理面相交時,穿透層理延伸的水力裂縫的縫高延伸速率顯著低于沿層理擴展的水力裂縫;侯冰等[19]采用實驗室試驗的方法,發現復雜的地質條件、脆性、發育的層理面和天然裂縫等會導致頁巖在壓裂后形成具有非平面、不對稱和多分支行為的復雜水力裂縫網絡。根據以上研究可知,鮮有針對施工參數(注液速率、液體黏度)對含層理頁巖水力壓裂過程中其水力裂縫擴展行為的影響規律研究。同時,考慮到理論分析無法對水力壓裂過程中所產生的復雜裂縫進行合理解釋,以及實驗室研究無法進行基于工程尺度的水力壓裂實驗研究[20-22],采用離散元法對含層理頁巖水力壓裂過程中其水力裂縫的擴展行為進行數值模擬研究,以揭示液體黏度和注液速率對其影響規律。
1 水力壓裂控制方程
頁巖氣儲層的水力壓裂過程是一個涉及孔隙、裂縫、流體、應力等多相介質的復雜流固耦合問題,而塊體離散元方法在模擬裂縫內的流固耦合行為上具有較高的優勢。綜合考慮本次數值模擬的研究目的可知,其控制方程主要涉及裂縫破壞的判定、節理內流體的流動及相關求解方程。
1.1 裂縫破壞判定
塊體離散元方法通過塊體間的節理面來模擬裂縫,節理面的破壞表示裂縫的開啟。節理的本構模型為庫倫滑移節理模型。在模型中均考慮了剪切和張拉失效,同時也考慮了節理的膨脹。在塊體離散元方法中節理通過接觸來描述,在彈性階段,接觸之間通過法向剛度與切向剛度來描述。節理的法向力學行為可表示為[23]:
式中:c為節理的黏聚力,MPa; φ為節理的摩擦角,(°)。
當節理上的力超過其抗拉或抗剪強度后,接觸失效,同時節理的抗拉強度以及黏聚力變為 0。此時節理面上的最大拉力和最大剪切力可表示為:

剪切位移會引起法向的位移變化,其關系可由膨脹角θ 來表征:
式中:ΔUn(dil)為膨脹引起的法向位移。
此時法向力應該綜合考慮膨脹的影響,法向力變為:
1.2 節理內流體流動
節理內的流體流動符合N-S方程。當2 個面近似平行的非滲透面,且流體為不可壓縮流體時,N-S方程可以簡化為雷諾方程[23]:
式中:u為平面上一點xi處的非滲透邊界的距離,u=u(xi) ;h為水頭高度,m; ρ為流體密度,kg/m3; μ為流體黏度,Pa?s;g為重力加速度,m/s2。
根據式(11)可得到流體的流速Vi方程為:
式中:u2/12為單裂縫滲透;kH為水力傳導率,kH=u3ρg/12μ。
1.3 數值求解
在水力壓裂中假設裂縫擴展行為主要由近尖端行為和流體整體體積平衡決定,裂縫擴展過程中主要有3 種能量耗散方式:流體流動過程中的黏性能耗散、產生新裂縫(巖石斷裂)所需的能量耗散以及流體濾失產生的能量耗散。對此,DONTSOV 等[23]給出了斷裂韌度、流體黏度和濾失的圓盤狀水力裂縫解模型。
以DONTSOV 等提出的求解模型為基礎并進行簡化,在不考慮流體慮失的條件下,可得到黏性控制機制下裂縫開度wm(ρ,t)和 裂縫半長Rm(t)的解析解分別為:

2 模型驗證
為了驗證塊體離散元方法在模擬水力壓裂中的可行性,基于上述2 種控制機制的求解方式,分別選取一定的頁巖屬性參數來進行模擬,并將數值計算所得到的裂縫開度分布值與理論解進行對比。數值模擬參數見表1,數值模擬結果與理論解對比如圖1。
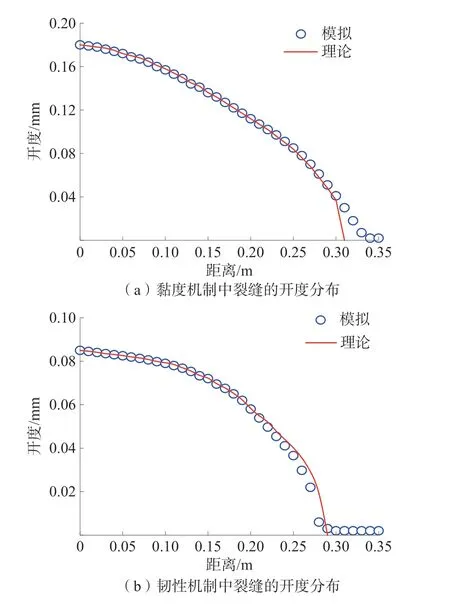
圖1 數值模擬結果與理論解對比Fig.1 Comparison between numerical simulation results and theoretical solutions

表1 數值模擬參數Table 1 List of numerical simulation parameters
從圖1 可以看出,無論是黏度控制機制,還是韌性控制機制,采用塊體離散元方法模擬所得到的裂縫開度分布的數值解與Donstov 所建立的近似理論解匹配度極高。因此,可以認為,塊體離散元法在頁巖水力壓裂中可以較好地模擬裂縫的擴展行為。
3 水力裂縫擴展行為數值模擬
3.1 數值模型
主要研究含層理頁巖在水力壓裂過程中,壓裂液黏度及注液速率對水力裂縫擴展行為的影響,故建立數值模型,數值模型如圖2。
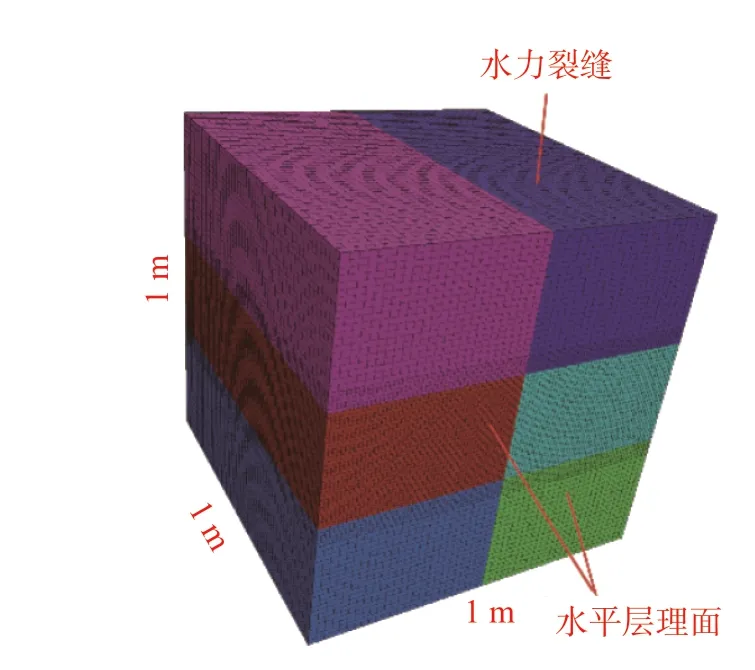
圖2 數值模型Fig.2 Numerical model
模型尺寸為1.0 m×1.0 m×1.0 m,模型中包含1 個垂向節理和2 個水平節理。其中,垂向節理則作為預置的水力裂縫,用以模擬水力裂縫的豎向擴展;水平節理用來模擬2 個水平層理面,2 個層理面間距0.3 m。注入點設置在垂向節理面的中心位置,注入點距離2 個水平層理面的距離相等。為了提高計算精度,在節理面附近進行網格加密。
此外,為了排除其他影響因素對模擬結果的影響,模擬中的地應力設置為均勻地應力(σx=σy=σz=20 MPa),節理參數設定為固定值(抗拉強度為10 MPa,黏聚力為5 MPa,摩擦角為20°),地層的流體壓力設定為10 MPa。頁巖的物理力學參數設定值分別為:密度2 600 kg/m3,彈性模量20 GPa,泊松比0.25。
3.2 數值模擬結果
3.2.1 壓裂液黏度
為探究壓裂液黏度對水力裂縫擴展行為的影響規律,將注液速率設置為3 mL/s,分別模擬不同壓裂液黏度(10~100 mPa·s,)下水力裂縫的擴展行為,不同壓裂液黏度時水力裂縫在豎向的擴展行為(注液速率為3 mL/s)如圖3。

圖3 不同壓裂液黏度時水力裂縫在豎向的擴展行為(注液速率為3 mL/s)Fig.3 Vertical expansion behaviors of hydraulic fractures under different fracturing fluid viscosity conditions(liquid injection rate is 3 mL/s)
從圖3 可以看出:當壓裂液黏度不超過65 mPa·s 時,水力裂縫未能穿過層理,且裂縫高度受到限制;當壓裂液黏度不低于66 mPa·s 時,水力裂縫穿過層理面并繼續豎向擴展,且裂縫高度不受限制。這說明壓裂液黏度會影響水力裂縫的穿層能力,低黏度有利于水力裂縫轉向層理擴展,而高黏度則有利于水力裂縫穿過層理。進而分析可知,壓裂液黏度對水力裂縫穿層行為的影響主要包含3 點:①壓裂液黏度會影響水力裂縫的分布形態,較低的壓裂液黏度有利于水力裂縫轉向,沿著水平層里面擴展,較高的壓裂液黏度則有利于水力裂縫的穿層,沿著豎向延伸;②壓裂液黏度會影響裂縫的開度,壓裂液黏度較低時,裂縫開度較小且變化梯度較小,隨著壓裂液黏度的增加,裂縫開度也會隨之增加,裂縫開度的分布梯度也會隨之增大;③壓裂液黏度會影響水力裂縫在水平層理面內的擴展,較低的壓裂液黏度有助于水力裂縫沿水平層理面延伸,壓裂液黏度越低,裂縫沿水平層理面的延伸距離越大。
3.2.2 注液速率
為探究注液速率對水力裂縫穿層能力的影響規律,在注液速率為3 mL/s 的基礎上,模擬1 組注液速率為30 mL/s 時不同壓裂液黏度條件下水力裂縫的擴展行為,并采用對比不同注液速率下水力裂縫在豎向的擴展來對其進行分析,不同壓裂液黏度時水力裂縫在豎向的擴展行為(注液速率為30 mL/s)如圖4。

圖4 不同壓裂液黏度時水力裂縫在豎向的擴展行為(注液速率為30 mL/s)Fig.4 Vertical expansion behaviors of hydraulic fractures under different fracturing fluid viscosity conditions (liquid injection rate is 30 mL/s)
從圖4 可以看出,當注液速率為30 mL/s 時,水力裂縫的穿層能力同樣表現出隨其壓裂液黏度的增加而增加的變化規律。此外,結合圖3 可知,注液速率為3 mL/s 時影響水力裂縫穿過層理的壓裂液黏度界限介于65~66 mPa·s 之間,而注液速率為30 mL/s 時影響水力裂縫穿過層理的壓裂液黏度界限則介于8~9 mPa·s 之間,這說明注液速率的增大,有效提高了水力裂縫的穿層能力,即大的注液速率更有利于水力裂縫穿過層理面。同時,當注液速率分別為3 mL/s 和30 mL/s 時,壓裂液黏度為100 mPa·s 時的裂縫開度分別為0.24 mm和0.37 mm,這說明隨著注液速率的增大,裂縫開度也隨之增加。
3.2.3 裂縫內壓力分布
在模型中布置4 個監測水力裂縫內壓力的觀測點,以便分析裂縫內的壓力分布特征。觀測點分布示意圖如圖5,其中,點1 為注入點所在位置,點4 位于豎向節理和橫向節理的相交線上。
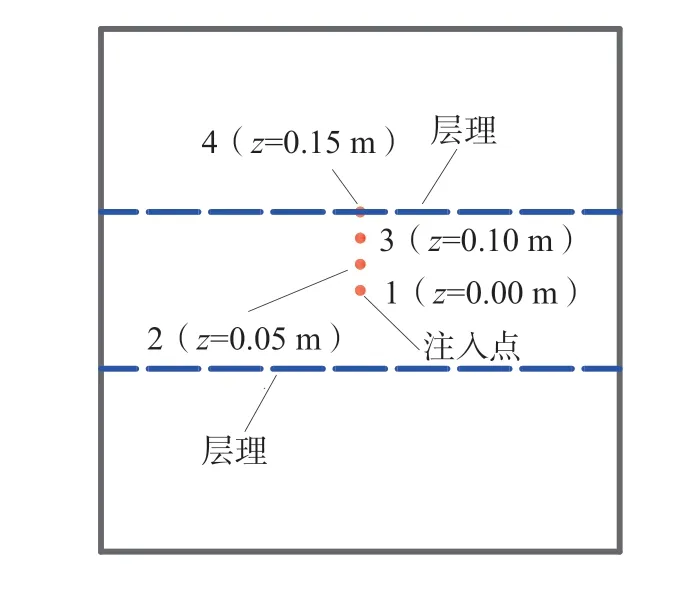
圖5 觀測點分布示意圖Fig.5 Distribution diagram of observation points
不同壓裂液黏度及不同注液速率下,裂縫內的壓力分布曲線如圖6。
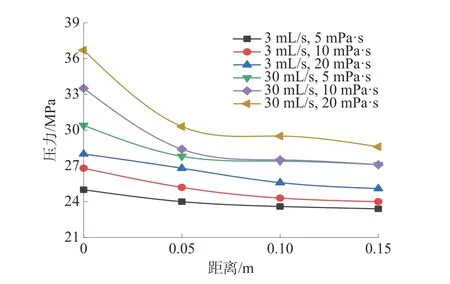
圖6 裂縫內的壓力分布曲線Fig.6 Pressure distribution curves in fracture
從圖6 可以看出:裂縫內的壓力從注入點向外逐漸降低,且在點 1 到點 2 之間(0.00~0.05 m)壓力曲線的變化梯度最大,壓力降低較快;而隨著裂縫的不斷擴展,向外側壓力衰減逐漸減慢;同時也可以看出,隨著壓裂液黏度和注液速率的上升,縫內壓力逐漸上升,且分布越來越不均勻。
4 結 語
1)基于塊體離散元方法所建立的數值模型能夠有效計算含節理頁巖氣儲層水力壓裂過程中的裂縫擴展問題。
2)較低的壓裂液黏度和注液速率時,裂縫內壓力較低且分布比較均勻,水力裂縫更傾向于轉向層理擴展;較高的壓裂液黏度和注液速率時,裂縫內壓力較高且分布差異大,此時水力裂縫更趨向于穿過層理面豎向擴展。
3)裂縫內的壓力從注入點向外逐漸降低,且隨著裂縫的不斷擴展,向外側壓力衰減逐漸減慢。

