帶學習效應、資源及工期分配的成組技術排序

摘"" 要：研究帶有學習效應、凸資源分配及不同工期分配的單機成組技術排序問題。為了提高生產效率，將工件按類分組，同一組內的工件可以分配不同的工期，工件的實際加工時間和組的實際安裝時間不僅與凸資源有關，還與學習效應有關。目的是確定組內工件的加工順序、組間的加工順序、最優資源分配量及最優DIF工期分配，在資源有限的條件下使提前、延誤和工期分配的總懲罰成本極小化。對于一般情況給出了目標函數表達式，對于一個特殊情況的問題，通過將其轉化為指派問題進行求解，給出了一個時間復雜度為O（n3）的多項式時間算法。

關 鍵 詞：成組技術; 學習效應; 資源分配; 不同工期分配

氧化鈷; 納米結構; 電容器; 電催化

中圖分類號：O343.1;O341""" 文獻標志碼：A

doi：10.3969/ j.issn.16735862.2024.01.012

Group technology scheduling problems with learning effects， resource allocation and due date assignment

CUI Song "LYU Yan "CHEN Lanfeng^1，2

ZHAO Yufang， GONG Dan

（1. College of Physical Science and Technology， Shenyang Normal University， Shenyang 110034， China）

（College of Mathematics and Systems Science， Shenyang Normal University， Shenyang 110034， China）

Abstract：

In this paper， we consider the single machine group technology scheduling problems with learning effects， unrestricted due date assignment method（DIF） and convex resource allocation. In order to improve production efficiency， the jobs are classified into groups， and the jobs in the same group can be assigned different due dates. The actual processing time of the jobs and the actual setup time of the group are related to the convex resource allocation and the learning effect. The goal is to determine the optimal job and group schedules， the optimal allocation of resources and the optimal DIF due date allocation， such that the total penalty cost of earliness， tardiness， and DIF due date assignment is minimized subject to limited resources availability. The objective function expression is given for the general case. And for a special case， it is solved by transforming it into an assignment problem， and an O（n3） polynomial time algorithm is given.

Key words：

group technology; learning effects; resource allocation; unrestricted due date assignment

成組技術利用任務的某種性質將任務分成若干組再進行加工以提高生產效率，它不僅需要確定各任務組之間的加工順序，還需要確定同組中每個任務之間的加工順序，以使目標函數值達到最優。Yoshida等^［1］首次提出了關于成組技術排序問題。隨后，成組技術問題受到了越來越多的關注。在傳統的排序問題中，工件的加工時間通常假設為常數。然而，在實際生產中會出現學習效應情況。Huang^［2］研究了帶惡化效應的雙準則單機成組技術排序問題，其中組的安裝時間和工件加工時間是開始加工時間的線性惡化函數。其目標中主要準則是總加權完工時間，次要準則是最大成本，并證明了問題可以在多項式時間內求解。Wang和Wang^［3］研究了帶釋放時間的單機成組技術排序問題，其中組的安裝時間和工件加工時間都是其開始加工時間的成比例線性函數，證明了最大完工時間問題可以在多項式時間內求解。Wang等^［4］研究了帶有縮短加工時間的單機成組技術排序問題。對于帶釋放時間的最大完工時間問題，證明了當組數固定時問題可以在多項式時間內求解，也給出了幾類多項式時間可解的特殊情況。對于線性成比例的最大完工時間問題，Lu等^［5］研究了帶有釋放時間的單機成組技術排序問題，其中組的安裝時間和工件的實際加工時間都是其開始加工時間的線性遞減函數，并證明了帶釋放時間的最大完工時間問題可以在多項式時間內求解，并且對于一般情況提出了啟發式算法。Kuo和Yang^［6］考慮了帶學習效應的單機成組技術排序問題，使最大完工時間和總完工時間極小化，并分別給出了在多項式時間內的最優算法。Lee和Wu^［7］研究了與位置相關的學習效應的單機成組技術排序問題，并提出了學習效應不僅取決于工件的位置，還取決于組的位置，并證明了最大完工時間和總完工時間問題仍然是多項式可解的。進一步，Zhang和Yan^［8］研究了具有惡化和學習效應的單機成組技術排序問題，證明了最大完工時間和總完工時間問題都在多項式時間內可解，其中學習效應不僅取決于工件位置，還取決于組中位置，而惡化效應取決于工件的開始時間。Kuo^［9］考慮了工件的實際加工時間與加工完工件的加工時間相關的學習效應及與位置相關的安裝時間學習效應的單機成組技術排序問題，對于最大完工時間問題分別給出了2種多項式時間算法，并在一定條件下給出了總完工時間的多項式時間最優算法。Yan等^［10］研究了帶有學習效應和資源分配的單機成組技術排序問題，目標是確定工件和組間的最優排序及最優資源分配，在有限資源條件下使總完工時間極小化，并證明了在某些特殊情況下問題是多項式可解的。

另外，在現代供應鏈管理中，由于當前制造業從批量生產向定制生產的轉變，以及人們對準時系統的興趣日益濃厚，工期分配問題引起人們的關注。由于生產能力有限，通常不可能在各自的工期內完成所有的任務，在工期之前完成加工的工件通常會產生提前成本（即儲存成本），而超過工期加工的工件會產生延誤成本。較早的工期對顧客更有吸引力，而較晚的工期可能會導致銷售損失，也有與工期分配相關的成本。因此，對于制造商來說，考慮所有相關成本并對總體成本進行優化是至關重要的。工期分配一般分為公共工期分配（common due date assignment method，CON）、松弛工期分配（slack due date assignment method，SLK）及不同工期分配（unrestricted due date assignment method，DIF）。Liu和Wang^［11］考慮了帶有SLK及CON和加工時間可控的成組技術排序問題，對于加工時間是線性資源和凸資源的函數，目標是使提前、延誤、2種工期分配及資源分配成本的加權總和極小化，證明了該問題可以在多項式時間內求解。Chen等^［12］考慮了帶有工期分配的單機成組技術排序問題，其中工期分配包括CON、SLK及DIF，目標是使提前、延誤、工期分配及完工時間的加權總和極小化，并證明了3種工期分配方法均可在多項式時間內求解。Chen和Cheng^［13］考慮了帶有凸資源分配和DIF的單機成組技術排序問題，目標是使提前、延誤、工期分配及資源分配成本的加權總和極小化，并證明了該問題可以在多項式時間內求解。在Chen和Cheng^［13］的基礎上，Chen等^［14］繼續考慮了帶有DIF和2種資源分配的單機成組技術排序問題，目標是使提前、延誤、工期分配和資源分配總成本極小化，對于凸資源和線性資源分配，證明了它們都在某種特殊條件下通過指派問題可以在多項式時間內求解。本文在Yan等^［10］和Chen等^［14］研究的基礎上進行了拓展，考慮帶有學習效應、凸資源分配及DIF的單機成組技術排序問題，目標函數是在總資源分配成本有限的條件下，使提前、延誤和DIF的加權總和極小化，在特殊情況下給出了多項式時間算法。

1 問題描述

設n個工件分為m組在一臺機器上加工，所有工件在0時刻都是可用的，且加工過程中不允許中斷。機器在某一時刻只能加工一個工件。在同一組內的工件是連續加工的，也就是一組工件全部加工完之后，才能加工下一組工件，且組內工件加工時不需要安裝時間。第i組記為Gi，其工件數記為ni，即∑mi=1ni=n，每組開始加工時需要一個安裝時間。Jij表示在i組中的第j個工件（i=1，…，m；j=1，…，ni）；dij和Cij分別表示其工期和完工時間。如果工件Jij排在第r組，則工件的實際加工時間為

pAij=（pijr^a1uij）v （1）

其中：pij為工件Jij的基本加工時間；a1≤0為工件的學習效應；uij為分配給Jij的資源量；v為給定的正實數。另外，當組Gi在給定排序中的第r個位置時，Gi的實際安裝時間為

sAi=（sir^a2ui）v （2）

在凸資源模型下，若分配的資源量uij或ui趨近于0，則工件的實際加工時間pAij或組的實際安裝時間sAi將趨近于無窮大，這不符合實際情況。因此，令uij≥uij，ui≥ui，其中uij和ui分別為分配給工件Jij和組Gi的資源量的下界。

對于組G［i］中工件排序π（J［i］［1］，…，J［i］［ni］），J［i］［j］（i=1，…，m； j=1，…，ni）為排在第i組中第j個位置的工件，用p［i］［j］和C［i］［j］表示J［i］［j］的基本加工時間和完工時間，d［i］［j］為工期，G［i］表示排在第i個位置的組，n［i］為其工件數，這里研究DIF模型，即在同組中的每個工件可以不受限制地分配不同的工期^［15］。本文需要確定的是組內工件的排序、各組之間的排序、最優的資源分配量及最優的DIF，目標函數為

∑mi=1∑ⁿⁱj=1（αijdij+βijEij+γijTij），在滿足資源約束∑mi=1∑ⁿⁱj=1uij≤和∑mi=1ui≤條件下求目標函數極小值，其中Eij=max{dij－Cij，0}和Tij=max{Cij－dij，0}，分別為工件Jij的提前和延誤，（gt;0）和（gt;0）是給定的資源總量，αij，βij和γij分別表示工期、提前和延誤的單位懲罰。用三參數表示法可以將問題描述如下：

1|GT，pAij=（pijr^a1uij）v，sAi=（sir^a2ui）v，∑mi=1∑nij=1uij≤，∑mi=1ui≤|∑mi=1∑nij=1（αijdij+βijEij+γijTij）（3）

其中GT表示成組技術。

2 初步結果

下面給出2個最優排序的性質。

引理1 對于問題式（3）的一個排序π，最優DIF工期分配d*（π）能夠通過下列規則得到：對于i= …，m；j= …，ni，當α［i］［j］lt;γ［i］［j］時，取d*［i］［j］（π）=C［i］［j］（π）；當α［i］［j］gt;γ［i］［j］時，取d*［i］［j］（π）=0；當α［i］［j］=γ［i］［j］時，d*［i］［j］（π）能取［0，C［i］［j］（π）］內的任意值。

引理2 問題式（3）存在一個最優排序，其中機器在加工過程中不空閑。

下面分析目標函數的表達式。

對于排序π，工件J［i］［j］的目標函數值記為Z［i］［j］（π，d*（π））。由引理1，對于i= …，m；j= …，ni，Z［i］［j］（π，d*（π））有以下3種情況：

1） 當α［i］［j］gt;γ［i］［j］時，取d*（π）［i］［j］=0，則E［i］［j］=max{d［i］［j］－C［i］［j］，0}=0；T［i］［j］=max{C［i］［j］－d［i］［j］，0}=C［i］［j］，因而Z［i］［j］（π，d*（π））=γ［i］［j］C［i］［j］；

2） 當α［i］［j］lt;γ［i］［j］時，d*（π）［i］［j］=C［i］［j］；T［i］［j］=E［i］［j］=0，故

Z［i］［j］（π，d*（π））=α［i］［j］C［i］［j］；

3） 當α［i］［j］=γ［i］［j］時，Z［i］［j］（π，d*（π））=α［i］［j］d［i］［j］+γ［i］［j］（C［i］［j］－d［i］［j］），即

Z［i］［j］（π，d*（π））=α［i］［j］C［i］［j］。

取ψ［i］［j］=min（α［i］［j］，γ［i］［j］），則Z［i］［j］（π，d*（π））=ψ［i］［j］C［i］［j］。

綜上，目標函數可以表示為

Z（π，d*（π））=∑mi=1∑n［i］j=1（ψ［i］［j］C［i］［j］）（4）

其中ψ［i］［j］=γ［i］［j］， 當α［i］［j］gt;γ［i］［j］α［i］［j］， 當α［i］［j］≤γ［i］［j］

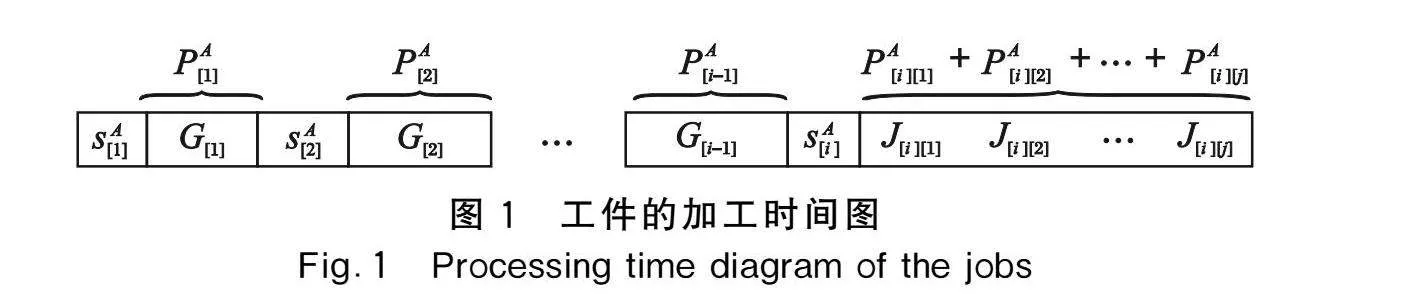
根據引理2，本文僅考慮機器在加工過程中不空閑的排序。設PA［k］表示組G［i］中所有工件的總加工時間，即PA［k］=∑l=1^n［k］pA［k］［l］。如圖1所示，工件J［i］［j］的完工時間為

C［i］［j］=∑i-1k=1PA［k］+∑ik=1sA［k］+∑jl=1pA［i］［l］=∑i-1k=1∑n［k］l=1pA［k］［l］+∑ik=1sA［k］+∑jl=1pA［i］［l］ （5）

將式（5）代入式（4）得

Z（π，d*（π））=∑mi=1∑n［i］j=1ψ［i］［j］（∑ik=1sA［k］）+∑mi=1∑n［i］j=1ψ［i］［j］（∑i－1k=1∑n［k］l=1pA［k］［l］）+∑mi=1∑n［i］j=1ψ［i］［j］（∑jl=1pA［i］［l］） （6）

又 ∑mi=1∑n［i］j=1ψ［i］［j］（∑ik=1sA［k］）=∑mi=1（∑mk=iΨ［k］）sA［i］ （7）

其中Ψ［i］=∑^n［i］j=1ψ［i］［j］是在組G［i］的所有工件ψ［i］［j］的和。

而" ∑mi=1∑n［i］j=1ψ［i］［j］（∑i-1k=1∑n［k］l=1pA［k］［l］）=∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］）pA［i］［j］（8）

且 ∑mi=1∑n［i］j=1ψ［i］［j］（∑jl=1pA［i］［l］）=∑mi=1∑n［i］j=1（∑n［i］l=jψ［i］［l］）pA［i］［j］" （9）

因此，將式（7-9）代入式（6）并整理得

Z（π，d*（π））=∑mi=1（∑mk=iΨ［k］）sA［i］+∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）pA［i］［j］（10）

將式（1）和式（2）代入式（10）得

Z（π，d*（π））=∑mi=1（∑mk=iΨ［k］）（s［i］i^a2u［i］）v+∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1u［i］［j］）v（11）

由式（11）可知，總懲罰成本Z（π，d*（π））是關于uij和ui的連續遞減凸函數。下面討論uij和ui的取值問題。

引理3 對于問題式（3），在排序π中，最優資源分配u*［i］［j］和u*［i］（i= …，m； j= …，ni）分別為

u*［i］［j］=［（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1）v］^1v+1∑mi=1∑n［i］j=1［（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）×（p［i］［j］i^a1）v］^1v+1×（12）

和u*［i］=［（∑mk=iΨ［k］）（s［i］i^a2）v］^1v+1∑mi=1［（∑mk=iΨ［k］）（s［i］i^a2）v］^1v+1×（13）

證明 由于式（11）是關于u［i］［j］和u［i］的凸函數，其中∑mi=1∑nij=1uij≤，∑mi=1ui≤，所以使用拉格朗日乘子法求解。拉格朗日函數為

L（u，δ，γ）=Z（π，d*（π））+δ（∑mi=1∑n［i］j=1u［i］［j］－）+γ（∑mi=1u［i］－）

=∑mi=1（∑mk=iΨ［k］）（s［i］i^a2u［i］）v+∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1u［i］［j］）v+

δ（∑mi=1∑n［i］j=1u［i］［j］－）+γ（∑mi=1u［i］－）（14）

其中δ≥0和γ≥0是拉格朗日乘子。先對L（u，δ，γ）中u［i］［j］和δ求導得

L（u，δ，γ）u［i］［j］=δ－v（（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1）v（u［i］［j］）^v+1）=0（15）

L（u，δ，γ）δ=∑mi=1∑n［i］j=1u［i］［j］－=0（16）

由式（15）和式（16）可得

u［i］［j］=v（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）δ^1v+1（p［i］［j］i^a1）^vv+1（17）

δ^1v+1=∑mi=1∑n［i］j=1［v（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）］^1v+1（p［i］［j］i^a1）^vv+1（18）

將式（18）代入式（17）得

u*［i］［j］=［（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1）v］^1v+1∑mi=1∑n［i］j=1［（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）（p［i］［j］i^a1）v］^1v+1×

同上，再對L（u，δ，γ）中u［i］和γ求導得

u［i］=v（∑mk=iΨ［k］）γ^1v+1（s［i］i^a2）^vv+1（19）

γ^1v+1=∑mi=1［v（∑mk=iΨ［k］）］^1v+1（s［i］i^a2）^vv+1（20）

將式（20）代入式（19）得

u*［i］=［（∑mk=iΨ［k］）（s［i］i^a2）v］^1v+1∑mi=1［（∑mk=iΨ［k］）（s［i］i^a2）v］^1v+1×，即結論成立。

將式（12）和式（13）代入式（11）得目標函數為

Z（π，d*（π））=^－v［∑mi=1（∑mk=iΨ［k］）^1v+1（s［i］i^a2）^vv+1］^v+1+

^－v［∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）^1v+1（p［i］［j］i^a1）^vv+1］^v+1（21）

為了討論方便，令

Z1=^－v［∑mi=1（∑mk=iΨ［k］）^1v+1（s［i］i^a2）^vv+1］^v+1

Z2=^－v［∑mi=1∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）^1v+1（p［i］［j］i^a1）^vv+1］^v+1

則Z（π，d*（π））=Z1+Z2。

引理4^［16］ 如果2個序列xi與yi是逆序的，也就是xi按不增（不減）排列，yi按不減（不增）排列，則它們的積之和∑xiyi可以取得最小值。

引理5 在問題式（3）的最優排序中，組G［i］內的工件按p［i］［j］不減的順序排序，即p［i］［1］≤p［i］［2］≤…≤p［i］［ni］。

證明 在Z（π，d*（π））=Z1+Z2中，Z1與工件無關；在Z2中，設

［i］［j］=（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）^1v+1i^va1v+1

由于∑mk=i+1Ψ［k］是定值，而∑n［i］l=jψ［i］［l］是關于j的單調遞減函數；又因在組G［i］中，同組內工件，i相同，v相同，a1相同，所以i^va1v+1相同，故φ［i］［j］是單調遞減函數。于是，在Z2的式子中，

∑n［i］j=1（∑mk=i+1Ψ［k］+∑n［i］l=jψ［i］［l］）^1v+1（p［i］［j］i^a1）^vv+1=

∑n［i］j=1（∑mk=i+1Ψ［k］+

∑n［i］l=jψ［i］［l］）^1v+1i^va1v+1p［i］［j］^vv+1=∑n［i］j=1［i］［j］p［i］［j］^vv+1

由引理4，在最優排序中組G［i］工件按p［i］［j］不減排序，即p［i］［1］≤…≤p［i］［ni］。結論成立。

3 特殊情況

定理1 對于問題式（3），如果a2=0，si=s，ψij=ψ，ni=nm=n*（i=1，…，m；j=1，…，ni），則組間排序π*G可以轉化為指派問題求解。

證明 根據引理5，在組G［i］內的工件按p［i］［j］不減的順序排序，即p［i］［1］≤…≤p［i］［ni］。對于Z1，若a2=0，si=s，v為給定的正實數，則（s［i］i^a2）^vv+1為定值；若ψij=ψ，ni=nm=n*，則Ψ［k］=∑^n［k］j=1ψ［k］［j］=∑^n*j=1ψ=n*ψ，故（∑mk=in*ψ）^1v+1=（（m－i+1）n*ψ）^1v+1，從而Z1為一個定值。對于Z2，由Ψ［k］=n*ψ，得∑mk=i+1Ψ［k］=∑mk=i+1n*ψ=（m－i）n*ψ，又由∑^n［i］l=jψ［i］［l］=∑^n*l=jψ=（n*－j+1）ψ，令

Ωil=∑^n*j=1（（m－l）n*ψ+（n*－j+1）ψ）^1v+1（pi［j］l^a1）^vv+1，則對于組間排序問題可以轉化為如下指派問題：

min ∑mi=1∑ml=1Ωilxil

s.t.∑mi=1xil=1，i= …，m

∑mi=1xil=1，l= …，m

xil=0，l，i= …，m；l= …，m（22）

因此，當a2=0，si=s，ψij=ψ，ni=nm=n*（i= …，m；j= …，ni）時，問題式（3）的組間排序π*G可以用指派問題求解。

4 算法及算例

在a2=0，si=s，ψij=ψ，ni=nm=n*（i=1，…，m；j=1，…，n*）的情況下，問題式（3）可以通過下列多項式時間算法求解：

算法：

步驟1 將各組工件按基本加工時間不減排序；

步驟2 根據式（12）和式（13）計算Ωil，通過指派問題式（22）得到組間的最優排序π*G；

步驟3 由式（12）和式（13）計算資源分配u*ij和u*i；

步驟4 通過引理1計算工件的最優工期d*ij。

定理2 如果a2=0，si=s，ψij=ψ，ni=nm=n*（i=1，…，m；j=1，…，n*），則問題式（3）能夠在O（n3）時間內求解。

證明 步驟1復雜度為O（mn*logn*）；步驟2計算Ωil（i=1，…，m；l=1，…，m）的復雜度不超過m2，因而求解指派問題的復雜度為O（m3）；步驟3計算最優資源分配的復雜度為O（n）；步驟4計算最優工期分配的復雜度為O（n）；由ni=nm=n*，得O（m）=O（n），則算法的總復雜度為O（n3）。

5 結 語

本文研究了具有學習效應、凸資源分配及DIF的單機成組技術排序問題，目標是確定每組中工件的最優排序和組間的最優排序及最優資源分配和工期分配。在資源有限的條件下，極小化提前、延誤、DIF總懲罰成本。在一定條件下給出了多項式時間算法，利用算法給出了工件的最優排序、組間的最優排序、最優的資源分配和工期分配。在今后的研究中，可以考慮對一般情況的求解方法，例如分枝定界算法等。

參考文獻：

［1］KRAJCINOVIC D，FONSEKA G U.The continuous damage theory of brittle materials［J］.J Appl Mech，1981，48（4）：809824.

YOSHIDA T，NAKAMURA N，HITOMI K.A study of production scheduling （optimization of group scheduling on a single production stage）［J］.Trans Japan Soc Mech Eng，1973，39：19932003.

［2］HUANG X.Bicriterion scheduling with group technology and deterioration effect［J］.J Appl Math Comput，2019，60：455464.

［3］WANG J B，WANG J J.Single machine group scheduling with time dependent processing times and ready times［J］.Inform Sci，2014，275：226231.

［4］WANG J B，LIU L，Wang J J，et al.Makespan minimization scheduling with ready times，group technology and shortening job processing times［J］.Comput J，2018，61（9）：14221428.

［5］LU Y Y，WANG J J，WANG J B.Single machine group scheduling with decreasing time-dependent processing times subject to release dates［J］.Appl Math Comput，2014，234：286292.

［6］KUO W H，YANG D L.Single-machine group scheduling with a time-dependent learning effect［J］.Comput Oper Res，2006，33（8）：20992112.

［7］LEE W C，WU C C.A note on single-machine group scheduling problems with position-based learning effect［J］.Appl Math Model，2009，33（4）：21592163.

［8］ZHANG X G ，YAN G L.Single-machine group scheduling problems with deteriorated and learning effect［J］.Appl Math Comput，2010，216（4）：12591266.

［9］KUO W H.Single-machine group scheduling with time-dependent learning effect and position-based setup time learning effect［J］.Ann Oper Res，2012，196：349359.

［10］YAN J X，REN N，BEI H B，et al.Study on resource allocation scheduling problem with learning factors and group technology［J］.J Ind Manag Optim，2023，19（5）：34193435.

［11］LIU W，WANG X.Group technology scheduling with due-date assignment and controllable processing times［J］.Processes，2023，11（4）：1271.

［12］CHEN Y，XU Y，ZHANG G，et al.A single machine group scheduling problem with due date assignment and position-dependent costs［J］.Asia Pac J Oper Res，2023，40（4）：20.

［13］CHEN Y，CHENG Y.Optimal due date assignment without restriction and convex resource allocation in group technology scheduling［C］//International Conference on Combinatorial Optimization and Applications.Cham：Springer International Publishing，2021：456467.

［14］CHEN Y，MA X，ZHANG G，et al.On optimal due date assignment without restriction and resource allocation in group technology scheduling［J］.J Comb Optim，2023，45（2）：64.

［15］SEIDMANN A，PANWALKAR S S，SMITH M L.Optimal assignment of due-dates for a single processor scheduling problem［J］.Int J Prod Res，1981，19（4）：393399.

［16］HARDY G H，LITTLEWOOD J E，POLYA G.Inequalities［M］.London：Cambridge University Press，1967.

【責任編輯：溫學兵】