一種基于一致性的分布式天基雷達組網空中目標高度估計與定位方法

王增福 邵 毅 祁登亮 金術玲

①(西北工業大學自動化學院 西安 710072)

②(西安航天動力試驗技術研究所 西安 710100)

③(中國電子科技集團公司第三十八研究所 合肥 230088)

1 引言

天基探測雷達具有全天候、全天時的戰略、戰術預警能力，且具有不受地球曲率限制、不易受攻擊等優勢，在預警防御系統中具有巨大潛力。本文考慮面向大范圍自主搜索發現任務的天基雷達。設計過程中，為了實現較好的最小可檢測速度，通常方位向孔徑尺寸較大；而綜合考慮重量、收攏等因素，俯仰向口徑尺寸較小，俯仰向測角能力較弱。因此，單個天基探測雷達對空中目標跟蹤定位時，相比于目標徑向距量測及方位角量測誤差，目標俯仰角量測誤差較大；僅利用單雷達徑向距量測、方位角量測、俯仰角量測難以有效估計空中目標高度。空中目標高度信息的缺失嚴重放大了目標定位誤差，同時不利于目標屬性判別與威脅估計。天基探測雷達空中目標高度估計研究較為少見。Graves[1]提出了一種基于多路徑干擾模式的天基雷達空中目標高度估計方法，理論上難以適用于低空目標。而通過多個天基探測雷達組網，融合利用多個天基探測雷達徑向距、方位角量測，可提高空中目標高度估計準確度，對改善目標定位精度及威脅估計能力等具有重要意義。

天基探測雷達目標定位涉及多次坐標轉換，具有較強的非線性，需要采用非線性濾波算法估計目標運動狀態。常見的非線性濾波方法有擴展卡爾曼濾波(Extended Kalman Filter,EKF)、無跡卡爾曼濾波(Unscented Kalman Filter,UKF)、轉換量測的卡爾曼濾波(Converted Measurement Kalman Filter,CMKF)和粒子濾波(Particle Filter,PF)等。Kulikov等人[2]基于全局誤差控制常微分方程(Ordinary Differential Equations,ODE)求解器提出了一種精確的連續離散EKF方法，在高維雷達目標跟蹤場景下對所提算法進行了驗證，數值結果表明該方法可用于實際的目標跟蹤，靈活度和魯棒性更高。Kulikov等人[3]和Zhang等人[4]采用無跡變換(Unscented Transform,UT)來近似非線性系統的狀態轉移過程和量測方程，結果表明其濾波精度要優于EKF方法。然而，EKF和UKF濾波器忽略了狀態協方差矩陣的欠估計問題，導致濾波精度下降。張連仲等人[5]采用一種基于期望最大化的轉換量測卡爾曼濾波方法，將球坐標系下的雷達量測值轉換到直角坐標系下，利用期望最大化方法修正了量測噪聲協方差，最后利用標準卡爾曼濾波器進行濾波，提高了野值干擾下的目標跟蹤精度，但該方法需要利用真值計算量測轉換誤差矩陣，進而導致兼容性問題。Wu等人[6]提出了一種重新加權的魯棒粒子濾波方法來降低量測野值對目標跟蹤精度的影響，結果表明該方法具有較高的跟蹤精度，但是，由于使用蒙特卡羅采樣，粒子濾波所需計算時間成本過高。Ait-El-Fquih等人[7]提出了一種基于變分貝葉斯(Variational Bayes,VB)的粒子濾波方法，該方法將VB方法與隨機抽樣技術相結合以分割狀態空間，從而推導出一種新的計算效率高的粒子濾波算法。閆文旭等人[8]在VB框架下，將系統狀態的后驗分布近似于一個可解的變分分布，通過迭代優化證據下界，并考慮懲罰因子調整迭代的步長，在非線性基礎上推導出閉合形式的迭代EKF。

近年來，概率圖模型及運行其上的消息傳遞方法得到了極大發展，并被應用于目標跟蹤定位問題中[9–11]。概率圖模型結合概率論和圖論，利用圖模型表示變量的聯合概率分布，利用條件獨立性將高維推斷問題分解，從而構造高效的學習和推斷算法。常見圖模型包括貝葉斯網絡、馬爾可夫隨機場以及因子圖，且它們之間可以相互轉化。同時，對于復雜推斷問題，具體的消息傳遞方法近年來也備受關注[12–15]，常見算法包括信度傳播(Belief Propagation,BP)、環信度傳播(Loopy BP,LBP)、變分消息傳遞(Variational Message Passing,VMP)、期望傳播(Expectation Propagation,EP)、非參數信度傳播(Nonparametric BP,NBP)、粒子信度傳播(Particle BP,PBP)、廣義信度傳播(Generalized BP,GBP)、平均場近似與信度傳播組合的消息傳遞等。

多天基雷達組網融合跟蹤本質上是一個復雜的推斷問題。考慮到天基平臺計算資源的稀缺性等實際需求，需要準確、低計算復雜度的融合跟蹤方法。鑒于因子圖模型對復雜推斷問題強大的表征能力，本文采用因子圖對多部雷達目標跟蹤問題進行建模，首先基于因子圖描述傳統的一致卡爾曼濾波，隨后引入耦合參數，并考慮到目標跟蹤模型的非線性特性，推導了分布式一致擴展卡爾曼濾波(Distributed Consistent Extended Kalman Filter,DCEKF)算法。隨后，針對EKF線性化非線性模型可能導致誤差變大的問題，在建立的因子圖的基礎上，利用分布式NBP (DCNBP)算法，有效解決了多雷達目標跟蹤的非線性問題，相較于DCEKF算法跟蹤精度明顯提升。

2 系統建模與問題描述

2.1 天基雷達目標跟蹤坐標系轉換

天基雷達提供的目標測量(徑向距、方位角和俯仰角)位于雷達測量坐標系，而常見的空中目標經度、緯度、高度信息在大地坐標系中描述。為了量測信息的統一，將大地坐標系向雷達測量坐標系轉換。首先是大地坐標系到地心(第4)赤道坐標系(簡稱ECEF坐標系)的轉換，本文采用近似迭代方法[16]，該方法具有更好的轉換效率和精度，并且在地球半徑50 km以內，不存在奇點和不收斂情況。下面介紹本文涉及的幾種坐標系及坐標轉換[8]。

如圖1所示，ECEF坐標系以地球球心O為原點，OXE軸指向0經度方向，OZE軸垂直赤道平面并指向地球自轉角速度方向，OXE,OYE與OZE軸構成右手法則坐標系。為了坐標轉換需要，同樣在圖1中建立地心(第1)赤道坐標系(簡稱ECI，又稱J2000.0坐標系)，其以地球球心O為原點，OXJ軸指向春分點，OZJ軸垂直赤道平面并指向地球自轉角速度方向，OXJ,OYJ與OZJ軸構成右手法則坐標系。天基雷達通常安裝在衛星上，故建立衛星軌道坐標系(簡稱LVLH坐標系)，其以衛星質心o為原點，oxL軸為地心指向衛星質心的衛星矢徑方向，ozL軸為衛星運動速度方向，oxL,oyL和ozL軸構成右手法則坐標系，下面介紹從ECEF坐標系到雷達量測坐標系的轉換步驟，坐標轉換的流程如圖2所示。

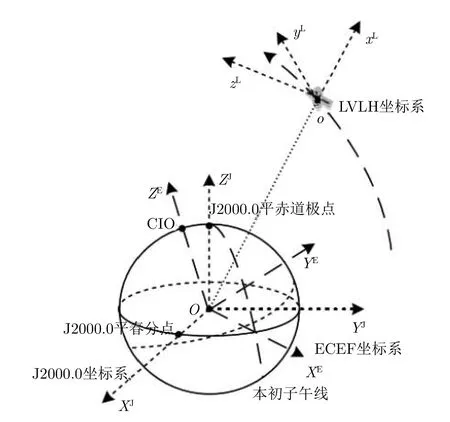
圖1 坐標系示意圖Fig.1 Coordinate systems

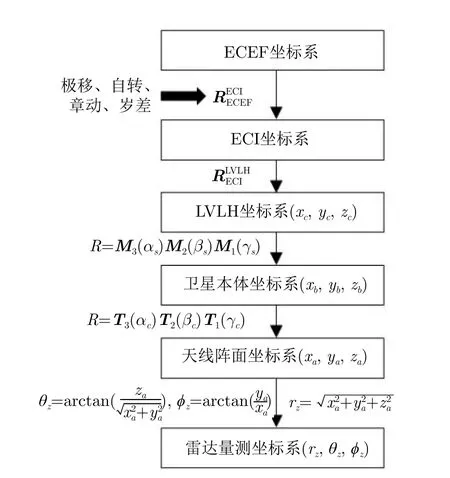
圖2 坐標系轉換流程圖Fig.2 Procedure of coordinate systems transformation

為了得到較為精確的坐標轉換，考慮地球的極移、自轉、章動、歲差的影響，從ECEF到ECI的坐標變換為

其中，[A],[B],[C] 和 [D] 分別為t0時刻的極移、自轉、章動和歲差矩陣，且

其中，xp和yp為地極坐標，θG為格林尼治恒星時角，εM,Δε和 Δ?分別為平黃赤交角、交角章動和黃經章動，Zp,θp和ξp為歲差參數，t0為歷元起始時刻，Rx(·),Ry(·)和Rz(·) 分別為繞x軸、y軸和z軸旋轉的方向余弦矩陣。

從ECI坐標系到衛星LVLH坐標系的旋轉矩陣為

其中，ν為緯度幅角，Ω和i為軌道傾角與升交點赤經。

衛星本體坐標系oxbybzb以衛星質心為坐標原點o，3軸為衛星的3個慣性主軸，oyb軸垂直于星箭分離面，ozb軸垂直指向星體對地面，oxb,oyb與ozb構成右手直角坐標系。理想情況下，衛星入軌姿態角全為 0°，衛星LVLH坐標系與衛星本體坐標系重合。衛星LVLH坐標系到衛星本體坐標系的轉換為

其中，γs,βs和αs分別為衛星在本體坐標系中姿態的滾動角、俯仰角和偏航角，M1,M2,M3分別為按照右手法則繞x,y,z軸逆時針旋轉一定角度的旋轉矩陣，xc,yc和zc為目標在衛星LVLH坐標系下的位置，xb,yb和zb為目標在衛星本體坐標系中的位置。

如圖3所示，天基雷達天線陣面坐標系oxayaza坐標原點o在天線中心，oxa軸指向天線橫軸，oya軸指向天線縱軸，oza軸指向天線陣面法向，oxa,oya與oza構成右手直角坐標系。一般天線安裝在衛星的對地面(通常天線陣面坐標系oxa的軸與衛星本體坐標系的oxb軸重合)，主要用于對地任務，入軌后轉動角度滿足對地工作要求，當所有陣面姿態角均為 0°時，天線陣面坐標系與衛星本體坐標系重合。衛星本體坐標系到天線陣面坐標系的轉換為

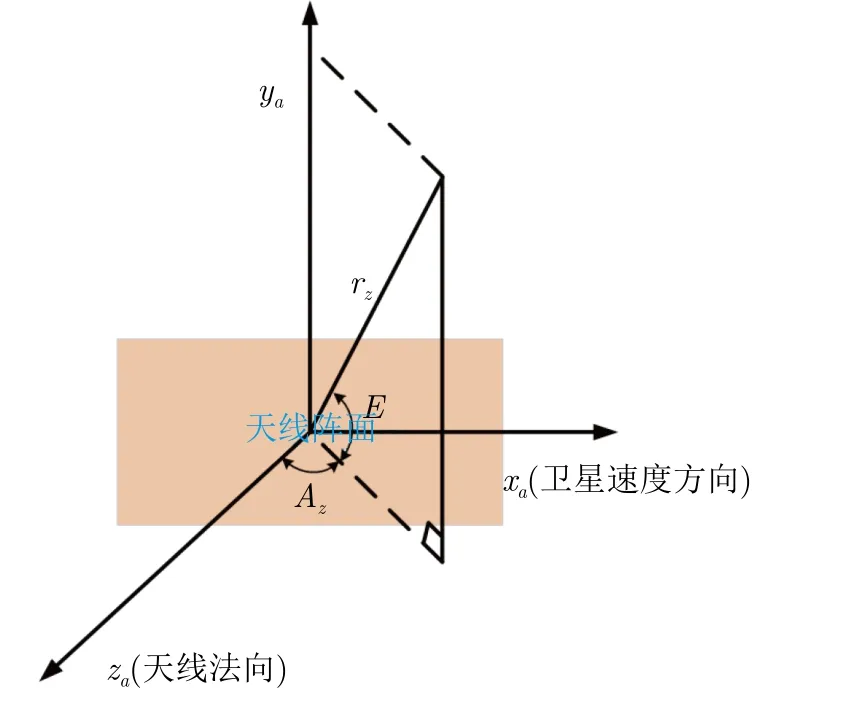
圖3 天基雷達天線陣面坐標系Fig.3 Space-based radar antenna array coordinate system

其中，γc,βc和αc分別為雷達天線陣面的滾動角、俯仰角和偏航角，xa,ya和za為目標在天線陣面坐標系下的位置，T1,T2,T3分別為按照右手法則繞x,y和z軸逆時針旋轉一定角度的旋轉矩陣。

雷達陣面測量坐標系為以天線中心為原點的球坐標系，從天線陣面坐標系到雷達量測坐標系的轉換為

其中，rz,θz和?z分別為雷達陣面測量坐標系下的空中目標的徑向距、方位角、俯仰角。

2.2 目標運動模型

不失一般性，考慮空中弱機動目標，此類目標的運動可以近似為勻速運動，其運動模型可以描述為

其中，xk為k時刻目標在ECEF坐標系下的位置速度矢量，，F為目標狀態轉移矩陣

其中，T為采樣間隔，ωk-1為過程噪聲，且假設ωk-1～N(0,Q)。

2.3 雷達量測模型

假設在k時刻共有N部天基雷達對目標進行測量，每部雷達得到的目標量測信息為徑向距、方位角。為了方便描述多雷達組網分布式融合中每個雷達的局部目標跟蹤，重寫目標運動模型式(7)如下。在第n個雷達節點，目標的運動模型可以近似為

由于俯仰角誤差較大，僅利用雷達徑向距和方位角量測估計目標高度及位置，第n個雷達在k時刻的量測方程表示為

2.4 基于因子圖的天基雷達組網目標跟蹤建模

因子圖是概率圖模型的一種。一般情況下，高維復雜隨機系統的推斷問題可以通過帶有局部交互函數的概率圖模型來建模，即利用因子分解方式和條件獨立性假設緊湊表示多個變量的聯合分布。因子圖模型中包含變量節點和因子節點，其中每個變量節點表示一個隨機變量，每個因子節點表示一個局部函數，連接變量節點和因子節點的邊表示該因子是該變量的函數。因子圖模型結合消息傳遞方法為解決復雜環境下的目標跟蹤與多源信息融合問題提供了統一框架，將復雜高維推斷問題轉換為優化問題，在估計精度、計算復雜度和實現的靈活性方面具有顯著優勢，能夠為目標跟蹤問題提供效果好、效率高和可擴展的統一解決方案。為此，在上述空中目標與天基雷達量測模型的基礎上，本文采用因子圖方法對天基雷達組網目標跟蹤進行建模。

其中，p(xk |xk-1)為狀態轉移概率分布函數，p(yk |xk)為似然函數。式(12)可以用因子圖4表示，其中，fk和hk分別表示k時刻狀態轉移函數和似然函數對應的因子節點。

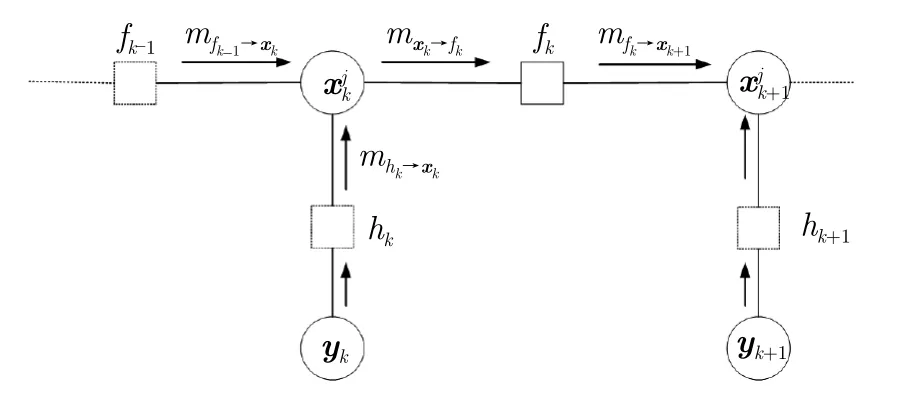
圖4 目標狀態與量測聯合概率分布函數的因子圖分解Fig.4 Factor graph decomposition of the joint probability distribution function of target states and measurements

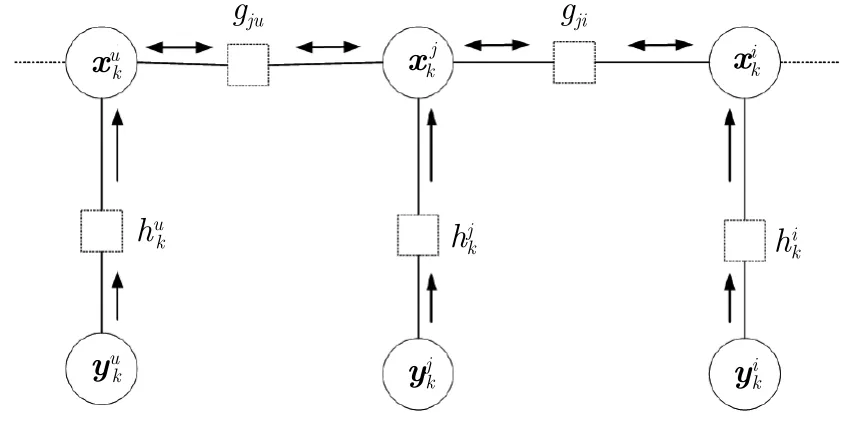
圖5 k 時刻局部因子圖模型Fig.5 A local factor graph model at time k

3 基于因子圖的分布式濾波算法

3.1 分布式一致擴展卡爾曼濾波

圖4所示因子圖模型中，k時刻，通過因子圖上的遞歸計算得到狀態xk的后驗邊緣分布和狀態xk+1的預測分布，即

式(13)與式(14)為目標全局狀態變量的更新與預測。根據2.3節的雷達觀測模型，在局部狀態變量中，引入一個耦合因子節點gji來表示全局變量xk的兩個復制狀態變量和在相鄰節點i和j上的關系，其中，i ∈Dj，Dj表示j的鄰居集合。將gji定義為一個指數函數[17]

因此，k時刻局部變量的后驗邊緣分布為

因子節點gji到變量節點的消息為

將式(15)和式(21)代入到式(20)中，可以得到迭代方程。初始化后，第l次迭代時的方程為

至此，完成了DCEKF算法推導，具體流程總結如算法1所示。

3.2 分布式非參數信度傳播算法

在DCEKF算法中，將量測方程式(10)中的非線性進行準線性化近似，以達到采用均值和方差表示消息的目的。但線性化近似可能產生較大損失，因此針對因子圖模型中的非線性、非高斯概率分布，結合信度傳播與粒子濾波，采用分布式非參數信度傳播算法(DCNBP)計算因子圖中的消息傳遞。在2.4節基礎上加入耦合函數后，k時刻的因子圖如圖6所示。

算法 1 天基雷達組網目標跟蹤DCEKF算法Alg.1 DCEKF algorithm for target tracking in space-based radar networks

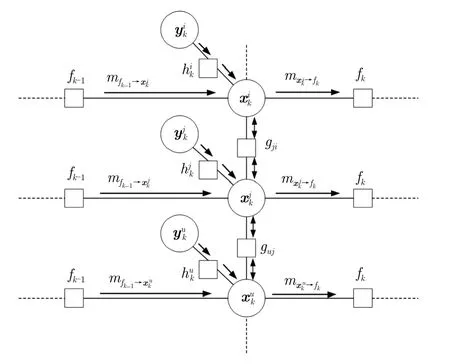
圖6 k時刻因子圖模型Fig.6 The factor graph at time k

其中，g-1(·)表示從雷達陣面坐標系到ECEF坐標系的轉換函數，且?z～U(0,2π)。因此，從因子節點傳遞至變量節點的消息為，其粒子化形式為

其中，N(x;xi,s,Pi)表示歸一化的高斯密度函數，均值和協方差分別為xi,s和Pi。式(41)中，S個高斯密度函數選取相同的協方差

因此，D個輸入消息的乘積可以表示為

易知，D個高斯密度函數的乘積仍然是一個高斯密度函數

因此，式(45)所示的高斯密度函數N(x;)的權重可以表示為

由式(40)可知，p(x)表示D個高斯混合式的乘積，每個高斯混合又含有S個高斯分量，則p(x)一共含有SD個高斯分量，直接采樣的計算復雜度為O(SD) 。因此，對D個高斯混合式的乘積采用重要性采樣[18]，引入輔助變量用來表示抽取樣本的高斯分量

且ζ1:D={ζ1,ζ2,...,ζD}。離散隨機變量ζi=li表示從第i個高斯混合式中的第li個高斯分量中抽取一個樣本，則式(40)可寫成

令重要性采樣的建議性分布為p(ζ1:D)，且

綜上，以線圖拓撲下的天基雷達網絡為例，基于DCNBP的天基雷達組網分布式目標融合跟蹤結構圖如圖7所示。每個雷達節點包含利用本地量測的目標跟蹤模塊以及利用其他節點估計值的融合模塊。初始化后，在k時刻，每部雷達在目標跟蹤模塊基于本地量測進行本地跟蹤。本地跟蹤后，每部雷達再根據相鄰雷達傳遞的本地跟蹤值與本地量測進行消息融合更新，經過多次迭代更新，實現多部雷達目標跟蹤的一致性融合。

算法 2 基于重要性采樣的消息乘積粒子化算法Alg.2 Message product particleization algorithm based on importance sampling

3.3 算法復雜度分析

本節通過計算執行的基本運算，比較分析DCEKF算法與DCNBP算法的計算復雜度。記目標的局部狀態向量大小為s，局部量測向量大小為M，DCNBP算法中粒子數為S，消息迭代次數為L。

對于DCNBP算法，每個節點的消息均為單獨計算，因此其狀態向量和量測向量維度為s和L。每個時刻，首先采用式(28)和式(29)生成帶權值粒子進行粒子初始化，生成粒子和權值的計算復雜度分別為s2S和s2+sS+s，從而該步每個節點的計算復雜度為O(s2S)。然后，采用算法2計算算法3中的所有消息乘積的粒子化形式。對于算法2，記節點的輸入消息個數為D，計算所有高斯混合消息的均值與協方差的復雜度為sS和s2DS2。根據設置輔助變量采樣粒子，式(46)和式(47)的計算復雜度分別為s3D+s2D+s2和sD+s2+2s。因此，D個輸入消息乘積的粒子化形式的計算復雜度為DS(s3D+s2D+sD+2s2+2s)。從而，算法2的計算復雜度為O(s2DS2+s3D2S)。因此，經過多次迭代計算每個節點消息的計算復雜度為O(s2LDS2+s3LD2S)。最后通過算法2計算每個節點的后驗分布。因此DCNBP算法的計算復雜度為O(s2LDS2+s3LD2S)。

算法 3 天基雷達組網目標跟蹤DCNBP算法Alg.3 DCNBP algorithm for target tracking in space-based radar networks

本文選擇3顆天基雷達測量空中目標的徑向距和方位角，單顆雷達的局部量測向量維度M與消息輸入個數大小D均較小。因此，DCEKF和DCNBP算法的計算復雜度分別為O(s3L)和O(s2S2L+s3LS)。可以看出，DCNBP算法的粒子數越多，計算復雜度相較DCEKF算法越大。

3.4 濾波初始狀態的選取與俯仰角先驗信息

在實際跟蹤中，濾波器初值的選取會對跟蹤性能造成極大的影響，空中目標俯仰角誤差過大是天基雷達目標定位的一個關鍵問題。

雷達得到的俯仰角誤差越大，得到的濾波器初值與真實值偏差就越大。本文利用幾何法[19]先求解目標高度h，再結合地球半徑re、徑向距rz和方位角θz估計目標俯仰角?z，由雷達與目標空間位置關系可知

其中，rs為雷達到地心的距離，(xc,yc,zc)為目標在LVLH坐標系下的坐標。實際天基雷達天線較多安裝在對地面，即陣面姿態角中僅滾動角變化較多，為簡化推導，僅假設滾動角γc非零，則

其中，(xa,ya,za)為目標在雷達陣面坐標系下的坐標，將式(52)代入到式(51)中，得

整理得

再將式(6)代入到式(54)，整理得

通過上述方法可估計出雷達量測的俯仰角信息，并估計出目標高度作為濾波算法初值。一方面提高了濾波算法初值精度，另一方面對于單部雷達將俯仰角估計值初值加入到量測方程中，可以部分解決單部雷達因為俯仰角缺失或誤差太大無法跟蹤目標的問題，但目標高度估計誤差仍然較大。

4 仿真與分析

本節通過仿真驗證DCNBP算法的性能，與幾何法、傳統集中式EKF (CEKF)、DCEKF算法、集中式粒子濾波(CPF)算法進行對比，基于高度求解結果對俯仰角進行估計并將其加入到量測，仿真驗證高度估計誤差對目標定位精度的影響。

4.1 仿真場景設置

考慮一個空中勻速直線飛行的目標，高度為9 km，采用3顆天基探測雷達對此空中目標進行跟蹤。3顆衛星軌道六根數，即軌道半長軸a，偏心率e，軌道傾角η，近地點幅角ω，升交點赤經Ω,平近點角M參數設置如下。衛星1：6978.14 km,1.369e–15,20°,0°,0°,50°；衛星2：7078.14 km,1.369e–15,20°,0°,0°,60°；衛星3：7178.14 km,1.369e–15,20°,0°,0°,70°；3顆衛星姿態角均為0°。3部天基雷達陣面姿態角均為滾動角 30°、俯仰角 0°、偏航角 0°。雷達量測噪聲標準差相同，根據典型的雷達與目標參數(脈沖寬度、方位向波束寬度等)取值，設置為徑向距0.09 km，方位角 0.03°。

設置迭代次數L=4 ；系統噪聲協方差均為Q=diag{10-3,10-3,10-3,10-3/T,10-3/T,10-3/T}，T=15 s；仿真得到目標在ECEF坐標系下的位置，并將其轉換到大地坐標系，得到目標高度估計。算法性能評估指標為空中目標高度的均方根誤差，即

其中，N表示蒙特卡羅仿真次數，取N=100，和hk分別表示k時刻目標估計高度和真實高度。在CPF算法中，令粒子數S=800。

4.2 結果分析

首先令耦合參數κ=500，粒子數S=800。CEKF、DCEKF、DCNBP、幾何法估計以及CPF的目標高度RMSE結果在圖8中給出，從圖中可以看出，幾何法的目標高度估計誤差最大，在1.5～3.0 km，這是因為僅采用了量測信息。集中式算法由于能夠利用全局信息，一般情況下，相比于分布式估計方法，具有更高的估計精度。因此，可以看到，傳統CEKF算法和CPF算法的精度最高，目標高度估計的RMSE為0.50 km和0.45 km。但實際工作時，集中式算法需要將所有量測信息與狀態信息發送到一顆衛星上進行數據處理，對該單星的通信負載與計算速率要求高，并且如果該星發生故障后，可能會導致整個系統失效，從而，對于天基雷達應用，包括CEKF,CPF算法在內的傳統集中式濾波器魯棒性與靈活性較差。而DCEKF,DCNBP等分布式濾波算法能更好地克服此類問題。圖8中，DCEKF算法、DCNBP算法高度估計RMSE分別為0.85 km和0.55 km。相比于DCEKF算法，DCNBP算法估計精度提升了35.3%，同時曲線波動更小，可見DCNBP算法不僅具有較高的估計精度，也具有較好的靈活性和魯棒性。本文未實現分布式PF算法，理論上，與DCNBP算法相比，分布式PF算法具有更高的估計精度，但計算量也更大；天基平臺計算資源較為稀缺，有必要在目標高度估計精度與計算量之間做出權衡。

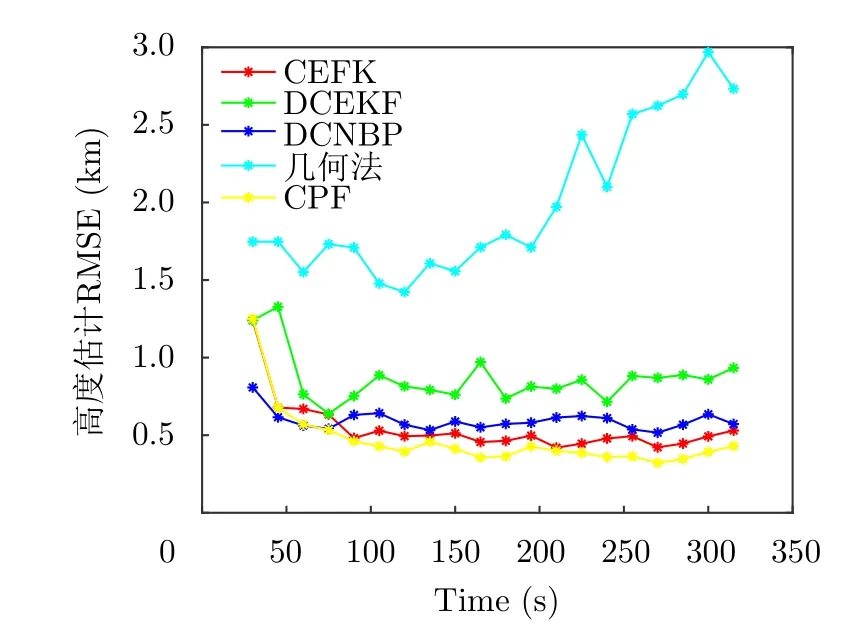
圖8 空中目標高度估計RMSEFig.8 RMSE of aerial target altitude estimation

DCNBP算法中，耦合參數κ和采樣粒子數S為關鍵參數，能夠影響算法估計性能。圖9和圖10分別為不同κ和S下DCNBP算法的目標高度估計結果，表1中列出了不同參數下算法估計的RMSE平均值。可以看出，隨著κ和S增大，DCNBP算法高度估計的RMSE變小，精度也越高。這是由于隨著κ的增加，相鄰變量的相關性越強，鄰居節點量測信息利用越充分，估計精度越好。而根據3.1節，當κ →∞時，局部變量與全局變量分布相同，高度估計精度并不會隨著κ的增加一直提高，其最終會趨于某一定值。同時當粒子數S越多，對非線性分布的近似誤差越小，最終的估計精度也更高，但S的增加也會提高算法的計算復雜度與通信負載，在應用當中需要根據實際情況進行權衡。

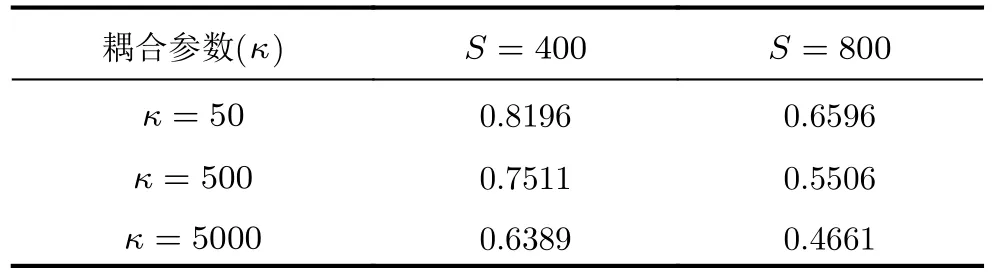
表1 不同參數下DCNBP算法估計的RMSE平均值(km)Tab.1 Average RMSE obtained by DCNBP with different parameters (km)

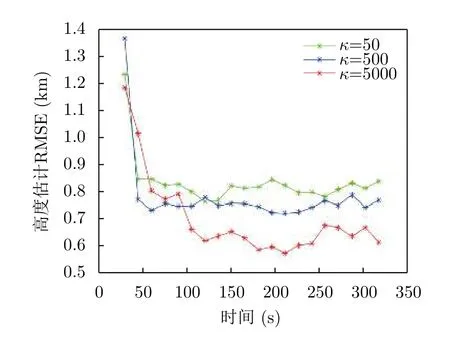
圖9 空中目標高度估計RMSE(粒子數 S=400)Fig.9 RMSE of aerial target altitude estimation(particle number S=400)

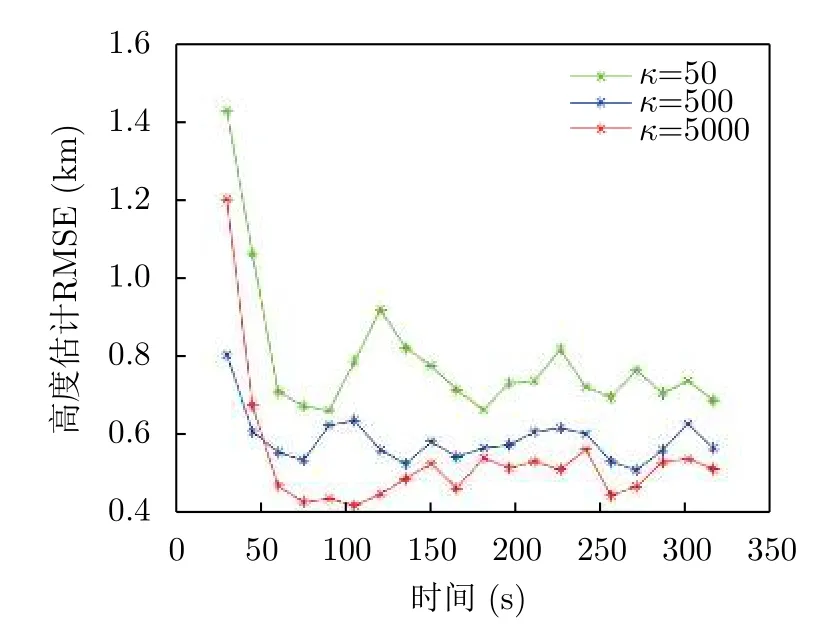
圖10 空中目標高度估計RMSE(粒子數 S=800)Fig.10 RMSE of aerial target altitude estimation(particle number S=800)

在天基雷達跟蹤目標過程中，雷達測量誤差與雷達到目標距離相關，因此分別取雷達對空中目標量測標準差為：徑向距0.07 km，方位角 0.02°；徑向距0.09 km，方位角 0.03°；徑向距0.11 km，方位角 0.04°。圖11所示為不同雷達測量誤差下DCNBP算法空中目標高度估計結果。由圖可知，當目標與雷達距離越近時，雷達量測誤差越小，目標最終的高度估計結果越精確。

前文中推導了基于高度估計的雷達俯仰角計算方法，該計算結果可以被認為是一個雷達偽測量值，高度估計越準確，該俯仰角偽量測值誤差就越小。為了進一步提高目標定位精度，將該偽測量值當作量測信息加入到濾波中，得到雷達徑向距、方位角與俯仰角信息，對空中目標進行定位估計。圖12為不同高度估計誤差下空中目標定位結果的RMSE。可以看出，高度估計誤差越大，俯仰角偽量測誤差越大，目標定位結果的RMSE也就越大；當高度估計誤差很大時，可等效為俯仰角信息缺失，此時，目標定位RMSE最大；隨著高度估計誤差的減小，俯仰角偽量測誤差逐漸減小，目標定位RMSE也逐漸減小，可知對目標高度估計越準確，加入俯仰角估計后的目標位置估計精度越高。由此可得，優先對目標高度進行估計進而得到雷達俯仰角偽測量值能夠彌補雷達在實際情況中俯仰角量測誤差大的缺點，進一步提高目標定位精度。

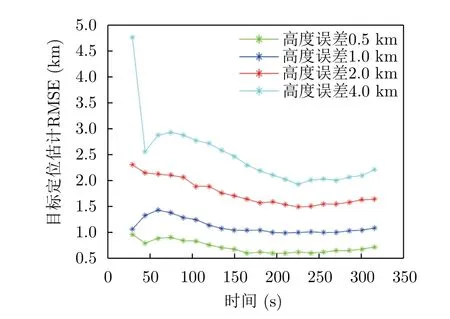
圖12 不同高度誤差空中目標定位估計RMSEFig.12 RMSE of aerial target position estimation with different altitude errors

5 結語

本文針對天基探測雷達空中目標定位時面臨的俯仰角信息缺失、量測非線性等問題，提出了一種基于一致性的分布式天基雷達組網空中目標高度估計與定位方法。首先建立了空中目標運動模型與天基雷達量測模型，并基于因子圖對傳感器目標跟蹤進行建模。考慮到雷達量測非線性，推導了基于因子圖消息傳遞的DCEKF算法；針對DCEKF對高非線性問題近似誤差大的問題，提出了基于采樣的DCNBP算法。仿真驗證表明，相較于DCEKFF、幾何法，DCNBP算法對目標高度估計精度更高。同時，分析了DCNBP算法參數對估計性能的影響。最后，根據得到的目標高度值估計出目標的俯仰角，并將該估計值當作偽測量估計目標位置。仿真結果顯示，目標高度估計越準確，加入俯仰角估計后的目標位置估計精度越高。

利益沖突所有作者均聲明不存在利益沖突

Conflict of Interests The authors declare that there is no conflict of interests