基于多臂賭博機的頻率捷變雷達在線決策方法

朱鴻宇 何麗麗 劉 崢* 謝 榮* 冉 磊

①(西安電子科技大學雷達信號處理全國重點實驗室 西安 710071)

②(江南機電設計研究所 貴陽 550009)

1 引言

隨著電子攻防對抗技術的迅速發展，雷達面臨著日益復雜的電磁干擾環境。噪聲壓制式干擾是最常用的有源電子干擾類型之一，對雷達目標探測造成了極大的威脅[1]。頻率捷變技術發揮了雷達在電子對抗中波形主動對抗優勢，具有優異的電子反對抗(Electronic Counter-Counter Measures,ECCM)性能[2]，是對抗噪聲壓制式干擾的有效手段。然而，傳統的頻率捷變雷達多采用固定或隨機的載頻跳變序列[3]，不能根據目標與電磁環境對載頻序列進行優化，從而限制了頻率捷變雷達在噪聲壓制干擾環境下的抗干擾能力[4]。

為了應對不同的干擾策略，如何設計智能的頻率捷變策略以提高雷達的檢測和抗干擾性能已經成為國內外學者越來越關注的問題[5]。傳統的雷達頻率捷變設計問題被描述為一個確定性的優化問題[6]，該類方法需要估計干擾和目標特性，以確定雷達的最優發射參數[7,8]。然而，在電子戰場景下的噪聲干擾通常是動態變化的，實時估計電磁環境參數對于資源有限的雷達通常是不切實際的。為了提高雷達對環境的適應能力，強化學習[9]被引入雷達抗干擾技術中。Selvi等人[10]將認知雷達與通信共存問題建模為一個馬爾可夫決策問題，并采用策略迭代法[11]解決該優化問題。Thornton等人[12]將深度強化學習引入雷達抗干擾中，實驗結果表明，在雷達與通信共存場景中，DQN (Deep Q-Network)算法[13]表現出更好的抗干擾性能。Ailiya等人[14]提出了一種基于強化學習的載頻和脈寬選取方案，以增強抗干擾性能。Li等人[15]設計了一種基于近端策略優化(Proximal Policy Optimization,PPO)算法[16]的子脈沖捷變方法，該方法通過發射誘導子脈沖欺騙干擾機并保護真實的探測信號，從而提高雷達抗干擾性能。盡管基于強化學習的頻率捷變方法獲得了較好的抗干擾性能，但仍存在以下缺點：(1)基于強化學習的頻率捷變方法需要進行離線訓練。強化學習的樣本效率是低下的[17]，需要經過大量交互樣本才能學習到較好的抗干擾策略，因此，將強化學習應用于雷達抗干擾中通常需要大量的離線探索來學習有效的頻率捷變策略，而這在雷達抗干擾場景往往是不切實際的。(2)基于強化學習的頻率捷變方法缺乏理論保證。基于強化學習的頻率捷變方法將雷達與干擾環境的交互過程建模為馬爾可夫決策過程，但干擾環境通常是一個時變的隨機過程，其馬爾可夫性質無法保證保持不變。此外，馬爾可夫決策過程隱含著決策者的行為會影響環境的未來狀態[18]。然而，在一些隨機干擾場景中，干擾環境的狀態可能與雷達的發射頻率獨立，此時，馬爾可夫決策過程的假設將不再成立。

為避免強化學習在雷達抗干擾決策應用中出現的問題，多臂賭博機[19](Multi-Armed Bandit,MAB)決策模型被引入雷達系統中。MAB算法是在線學習算法的一個重要分支[20]，由于其簡單性和理論上的性能保證，已經在無線信道選擇[21,22]、動態頻譜接入[23,24]等領域展現出巨大的應用前景。目前，MAB在雷達中的應用還處于起步階段，文獻[25]基于組合式MAB算法設計了信道信噪比未知的MIMO雷達收發單元子集選擇問題，該方法可以有效地用于求解MIMO雷達收發單元子集選擇問題。文獻[26]基于置信區間上界(Upper Confidence Bound,UCB)[27]算法設計了一種相控陣雷達目標搜索策略，該方法可以提高發現目標的概率。文獻[28]基于湯普森采樣(Thompson Sampling,TS)[29]和EXP3 (Exponential weights for Exploration and Exploitation)[30]算法設計了雷達波形選擇方法，有效提升了雷達的檢測和跟蹤性能。文獻[31]基于折扣湯普森采樣算法設計了一種非平穩環境下頻率捷變雷達發射策略，提高了雷達在非平穩環境中的檢測性能。上述研究表明了MAB算法在雷達在線決策問題上具有巨大的潛力。

然而，現有的MAB算法存在一定的局限性：一方面，TS類和UCB類算法對干擾策略極為敏感，在面對動態干擾場景時，學習性能不理想；另一方面，EXP3類算法在面對靜態干擾場景時，由于收斂速度較慢，而選擇大量的次優頻率通道，導致學習性能降低。在實際應用中，由于無法提前獲取敵方的干擾策略，此時使用其中一類算法可能會造成較大的性能損失。

因此，如何在沒有干擾環境先驗信息的條件下，設計一種適用于任意干擾策略的頻率捷變雷達在線決策方法是一個重要且具有挑戰性的問題。為了解決這個問題，本文根據干擾策略的特征，將雷達所面臨的干擾場景分為3類，針對3類干擾場景下的干擾策略特征，提出一種基于MAB的頻率捷變雷達在線決策方法。該方法在沒有探測環境先驗知識和離線訓練的情況下仍能實現優異的學習性能，且在3類干擾場景中均具有理論上的遺憾性能保證，在提升頻率捷變雷達探測和抗干擾性能方面具有重要的應用前景。

2 問題描述

2.1 雷達檢測模型

在噪聲壓制式干擾存在的情況下，雷達接收到的信號由目標信號、壓制式干擾信號和噪聲信號3部分構成[32]。根據雷達方程[33]，對于一個點目標回波信號的功率ys為

其中，Pt為雷達發射功率，G為發射天線增益，λ為雷達發射信號波長，σ為目標的散射截面積(Radar Cross Section,RCS)，Ls為雷達系統損耗，R為雷達與目標之間的距離。

雷達的接收機內部噪聲yn為

其中，k=1.38×10-23J/K為玻爾茲曼常數，T0為標準室溫，一般取290 K，Bn為接收機帶寬，Fn為接收機的噪聲系數。

根據干擾方程[34]，雷達接收到來自干擾機發射的干擾信號功率yJ為

其中，PJ為干擾機的發射功率，λj為干擾信號波長，G(θ)為雷達在干擾機主瓣方向上的天線增益，GJ為干擾機天線增益，γJ為極化失配損失，LJ為干擾系統損耗，Rj為雷達與干擾機之間的距離，表示干擾機的發射帶寬，表示雷達接收機接收到的干擾信號帶寬。

此時，雷達對目標的檢測概率Pd可近似為[33]

2.2 頻率捷變雷達MAB問題描述

將頻率捷變雷達的跳頻帶寬分為互不重疊的N個頻率通道。令F={f1,f2,...,fN}表示雷達可用載頻集，其中，fi=f0+(i-1)·B,i ∈{1,2,...,N}，f0為雷達初始載頻，B為雷達發射信號帶寬，頻率捷變雷達在每個脈沖重復周期內可從N個可用載頻內中任選一個作為雷達的發射載頻。假設雷達的發射功率不變，則在第t個脈沖重復周期內，雷達的發射參數可用向量A(t)=[a1(t)a2(t) ...aN(t)]表示，其中，ai(t)∈{0,1}為二元變量，用于表示雷達是否選擇第i個頻率通道用于探測。圖1為雷達發射頻率通道選擇示意圖，其中N=10,A=[0 1 0 0 0 0 0 0 0 0]，代表雷達選擇第2個頻率通道來發射。

研究頻率捷變雷達在線決策的目標是最大化雷達的探測性能，本文將檢測概率作為頻率捷變雷達MAB問題的獎勵值。在其他參數一定時，每個頻率通道的檢測概率由該頻率通道的目標的RCS值和干擾能量共同決定，考慮到頻率捷變雷達通常不具有對整個跳頻帶寬信號頻譜的同時感知能力，且在對抗中雷達難以提前獲取目標的RCS值，在每次探測中，獎勵值應只對發射頻率通道的檢測概率進行計算，不應對整個跳頻帶寬進行頻譜感知。另一方面，在壓制式干擾存在的情況下，目標信號可能被壓制干擾淹沒，導致雷達無法檢測到目標，從而無法利用式(4)計算檢測概率。因此本文設計了如下的獎勵函數：

其中，gt(fi)代表第t個脈沖重復周期雷達選擇第i個頻率通道獲得的收益值；ct ∈{0,1}為二元變量，用于表示第t個脈沖重復周期的回波信號中是否檢測出目標信號；SINRt(fi)表示第t個脈沖重復周期雷達接收到回波信號的信干噪比。

頻率捷變雷達MAB問題可描述如下：在第t個脈沖重復周期，雷達根據跳頻策略πt從可用載頻集F中選擇一個載頻fi作為雷達的發射載頻，接收回波信號并計算當前頻率通道的收益值gt(fi)，根據收益值選擇下一脈沖重復周期雷達的跳頻策略πt+1。頻率捷變雷達MAB問題一個基本挑戰是解決探索與開發之間的權衡[35]，即在利用過去獲得最高收益的動作與探索未來可能獲得更高收益的新動作之間取得平衡。MAB算法的性能用遺憾值R(t)衡量[19]，遺憾值R(t)定義為在t個脈沖重復周期內，MAB算法計算出的跳頻策略與使用最優固定頻率通道之間的累計增益差值：

其中，gs(fi)表示第i個頻率通道在第s個脈沖重復周期的收益值，gs(πs) 表示雷達在應用策略πs時在第s個脈沖重復周期的收益值。由于收益值gt和策略πt通常是隨機的，遺憾值R(t)是一個隨機變量，本文采用期望遺憾值衡量本文的算法性能：

由式(5)可知，收益值gt ∈[0,1]為有界函數，令損失值lt=1-gt，可以將收益值gt轉換為損失值lt，期望遺憾值Rˉ(t)也可以寫為損失值的形式：

2.3 噪聲壓制式干擾場景分類

與頻率捷變雷達發射模型相似，干擾機的發射通道選擇可用向量J(t)=[j1(t)j2(t) ...jN(t)]表示，其中，ji(t)∈{0,1},i=1,2,...,N為二元變量，用于表示干擾機是否選擇干擾第i個頻率通道。同時，假設干擾機在每個頻率通道內的干擾功率用向量Pj(t)=[pj,1(t)pj,2(t) ...pj,N(t)]表 示，其中，pj,i(t)∈為干擾機最大發射功率。則在第t個脈沖重復周期內，干擾機的發射策略可表示為

其中，?表示Hadamard積。

一般而言，壓制式干擾通常根據干擾帶寬和干擾信號的中心頻率分為瞄準式、阻塞式和掃頻式3種干擾策略。然而，一方面，該分類方法僅關注干擾機的干擾通道選擇策略J(t)，未考慮干擾功率變化對雷達跳頻策略造成的影響；另一方面，該分類方法不能全面地描述干擾機的干擾策略，實際干擾機可以根據雷達的發射策略，對上述的基本形式進行組合，如多點頻瞄準式干擾、分段阻塞式干擾等。

因此，本文從干擾策略的角度出發，根據干擾機的發射策略I(t)是否隨時間改變以及干擾機是否根據雷達的發射策略實施針對性的干擾，對干擾場景進行分類。

本文將雷達所面臨的噪聲壓制式干擾場景分為以下3類：

(1) 靜態干擾場景

在靜態干擾場景中，干擾機的干擾策略I(t)不隨時間改變。由于干擾機在每個頻率通道內的干擾功率不隨時間改變，因此，每個通道的損失值lt(fi)僅由干擾功率和目標RCS決定且不隨時間改變，即lt(fi) 服從一個只依賴于通道fi，而不依賴于時間t的獨立隨機分布。此時，干擾環境滿足隨機性MAB問題的假設，常用的求解算法為UCB算法和TS算法，在隨機性MAB問題中具有 ln(t)階的遺憾值上界。

在該類干擾場景下，使用μ(fi)=E[lt(fi)]表示第i個頻率通道的期望損失，若頻率通道f*滿足

令Nt(fi)表示前t輪交互中，第i個頻率通道被雷達選擇的次數，則靜態干擾場景下的期望遺憾值也可寫為

值得注意的是，無干擾的探測環境也可視為靜態干擾場景的一種特例，此時，各頻率通道內的期望損失值僅受目標RCS影響。

(2) 非自適應干擾場景

與靜態干擾場景不同，在非自適應干擾場景下，干擾機的干擾策略I(t)隨時間變化，即被干擾頻率通道以及干擾功率都可能隨著時間變化。在非自適應干擾場景下，可假設干擾機是一個非自適應的干擾機，即干擾機的干擾策略不會對雷達發射策略做出反應，是一種簡單的攻擊模型。

由于每個頻率通道的損失值lt(fi)受干擾機的干擾策略影響，每個通道的損失值lt(fi)不只依賴于通道fi，還與時間t有關。此時，干擾環境滿足對抗性MAB問題的假設，常用的求解算法為EXP3算法，在對抗性MAB問題中具有階的遺憾值上界。

(3) 自適應干擾場景

與非自適應干擾場景不同的是，我們假設干擾機是一個自適應干擾機，即干擾機可以觀測到雷達的發射策略，并針對性地設計干擾策略，此時，每個通道的損失值lt(fi) 與雷達的前t-1個發射頻率通道選擇有關。與非自適應干擾場景相比，自適應干擾場景對頻率捷變雷達具有更大的威脅。

文獻[36]表明，對于具有無限記憶內存的自適應干擾機，它可以模仿并執行與雷達相同的學習算法，并設置與雷達頻率通道選擇概率相同的策略對雷達進行干擾，這將導致遺憾值隨時間t線性增長。因此，本文考慮一個介于非自適應干擾機和無限記憶內存的自適應干擾機之間干擾模型：m-內存的自適應干擾機模型[36]，該模型下干擾機僅會記錄m個雷達最新的發射頻點，并依賴于這些觀測值對雷達進行干擾。

圖2給出了噪聲壓制干擾場景的示意圖，其中，紅色為雷達的發射頻率通道，藍色為干擾機的干擾頻率通道，紫色代表雷達發射頻率通道與干擾機干擾通道重合。其中，無干擾環境可以看作靜態干擾場景的一種特例。

3 基于MAB的頻率捷變雷達在線決策算法

3.1 算法描述

如2.3節所述，根據干擾策略的特征，雷達所面臨的噪聲壓制式干擾場景可分為3類。在靜態干擾場景中每個頻率通道的損失值服從一個不隨時間改變的隨機過程，這滿足隨機性MAB問題的假設；而在非自適應干擾場景和自適應干擾場景中，由于干擾策略不斷變化，每個頻率通道狀態被敵方干擾機任意控制，這滿足對抗性MAB問題的假設。隨機性MAB問題和對抗性MAB問題是MAB問題的兩種主要形式[37]，由于兩種問題的損失值確定形式不同，因此分析方法和性能結果存在明顯差異。經典的EXP3算法、UCB算法和TS算法均只能在其中一種MAB問題上保證最優的遺憾性能。而在實際場景中，無法提前判斷雷達所面臨的干擾環境屬于哪一種干擾場景，此時采用其中一種問題假設可能導致學習性能不佳。

本節中，我們將基于EXP3++算法[38]，設計一種頻率捷變雷達在線決策方法，該方法引入參數εt對每個頻率通道的選擇概率進行單獨的調整，提高了靜態干擾場景下選擇最優頻率通道的概率；同時，該方法的頻率通道選擇策略為指數分布和參數εt組合構成的分布，使得具有在非自適應干擾場景和自適應干擾場景下均具有良好的學習性能。本文將該算法命名為RAFA-EXP3++(Radar Adaptive Frequency Agility based on EXP3++)算法，具體的流程如算法1所示。

3.2 遺憾性能分析

在本節，將分析該算法在上述3類干擾場景中的遺憾性能。

(1) 靜態干擾場景下遺憾性能分析

算法1 RAFA-EXP3++算法Alg.1 RAFA-EXP3++algorithm

由于本文所提方法中ηt=2βt，因此，在靜態干擾場景中，本文所提方法的遺憾值滿足式(15)，為 (lnt)3階的遺憾值上界。

值得注意的是，當Δ(fj)較小時，會導致次優頻率通道的選擇次數增加，由式(10)可知，在靜態干擾場景下會造成較大的遺憾值。

(2) 非自適應干擾場景下遺憾性能分析

在非自適應干擾場景中，由于干擾機的干擾策略隨時間改變，每個通道的損失值受干擾機的干擾策略影響，滿足對抗MAB問題的假設。參考文獻[38]中定理1的證明過程，可以獲得如下的遺憾值上界：

由式(18)可以看出，在非自適應干擾場景下，本文所提方法具有階的遺憾值上界，與EXP3算法相同，因此，本文所提方法在非自適應干擾場景下可獲得與EXP3算法相近的學習性能。

(3) 自適應干擾場景下遺憾性能分析

如前文所述，對于一個無限內存的自適應干擾機，任何MAB算法都無法令遺憾值隨時間t次線性增長。在自適應干擾場景中，考慮一個m-內存的自適應干擾機，根據文獻[36]中的定理2可知，通過將整個時間t分為大小為τ的連續且不相交的批次進行處理，并利用該小批次受到的平均損失來反饋給RAFA-EXP3++，則當時，本文所提方法的遺憾值上界為

對比式(19)和式(18)可以看出，自適應干擾場景的算法遺憾值更高，說明自適應干擾場景將對雷達造成更大的威脅。

4 仿真結果及分析

4.1 參數設置

在本節將利用仿真實驗驗證2.3節的3類壓制干擾場景下所提頻率捷變雷達在線決策方法的性能。所有實驗均重復進行10次，每次仿真的脈沖數為105個。所有實驗結果均與隨機捷變策略(Random)、ε-Greedy算法[9]、UCB1算法[27]，EXP3算法[30]以及文獻[31]中的CDTS算法進行比較。其中，隨機捷變策略指雷達均勻隨機地選擇發射頻率通道，該策略是頻率捷變雷達的常用策略。ε-Greedy算法中探索率設置為0.1。UCB1算法是隨機性MAB問題中的常用算法，仿真實驗的雷達參數見表1。

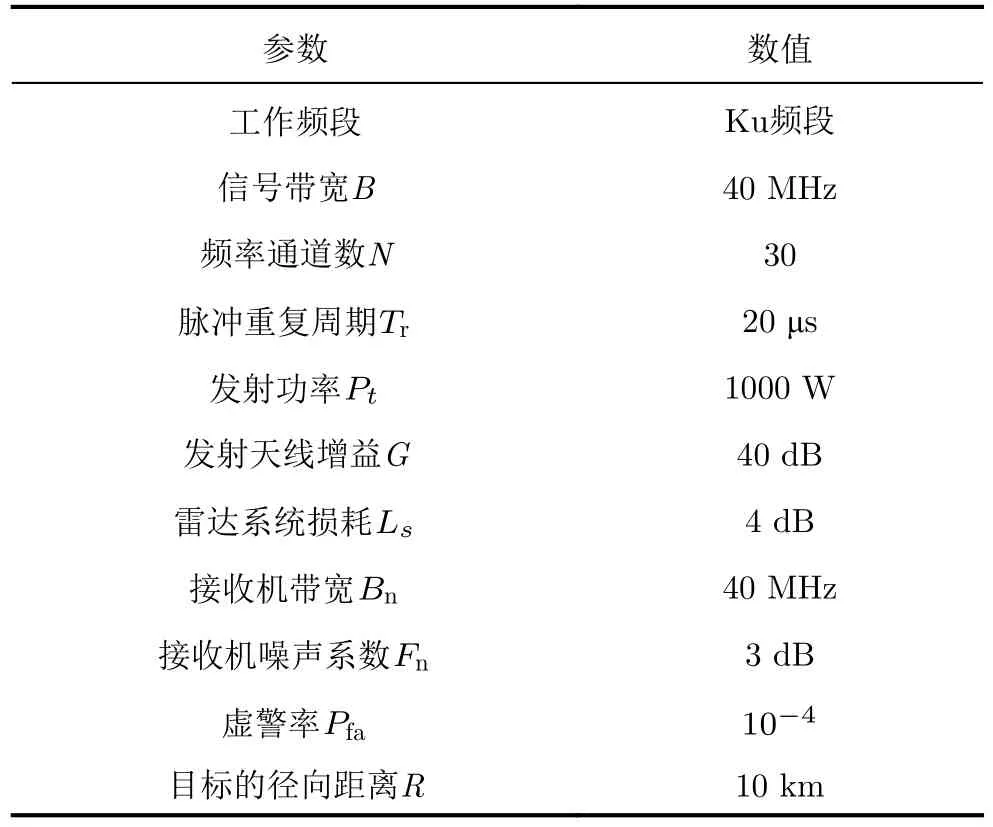
表1 仿真實驗雷達參數Tab.1 Radar parameters of simulation experiment

目標的RCS對電磁波頻率的變化極為敏感。不失一般性，假設目標的RCS是起伏的，起伏模型為Swerling II型，在各頻率通道內的RCS均值如表2所示。其中，U(a,b)表示服從在a到b之間均勻分布。

表2 仿真實驗中目標RCS均值(m2)Tab.2 The mean RCS of target in the simulation experiment (m2)

表3給出干擾機的部分仿真參數，其他參數在仿真實驗部分給出。

表3 仿真實驗干擾機部分參數Tab.3 Jammer parameters of simulation experiment

4.2 靜態干擾場景仿真結果及分析

為了驗證本文提出的算法在靜態干擾場景下的性能，在本節設計了無干擾以及固定干擾策略兩種干擾場景。

首先驗證無干擾場景下本文所提方法的性能。從圖3可以看出約有95%的發射信號選擇了SNR最高的頻率通道，有效避免了由于選擇次優頻率通道而降低雷達探測性能的問題。圖4為各算法的性能對比圖，其中，實線代表10次重復實驗的平均值，陰影部分為平均值±標準差后的邊界范圍。從圖中可以看出，隨機捷變策略的性能最差，這是由于隨機策略為均勻隨機選擇各頻率通道，而不是選擇收益最大的頻率通道，因此在無干擾場景中檢測性能較差。本文所提方法在無干擾場景下具有較低的遺憾值，與UCB1算法和CDTS算法的性能相近，與EXP3算法相比遺憾值降低90%。可以看出，在無干擾場景下本文所提方法優于EXP3算法和隨機捷變策略。

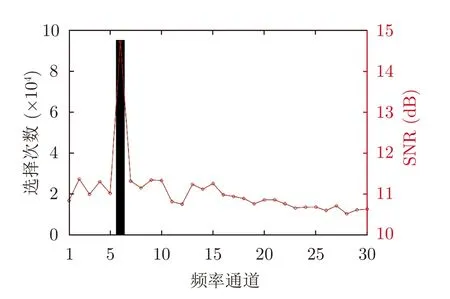
圖3 無干擾環境下頻率通道選擇次數與SNRFig.3 Frequency channel selection times and SNR in the no jamming environment

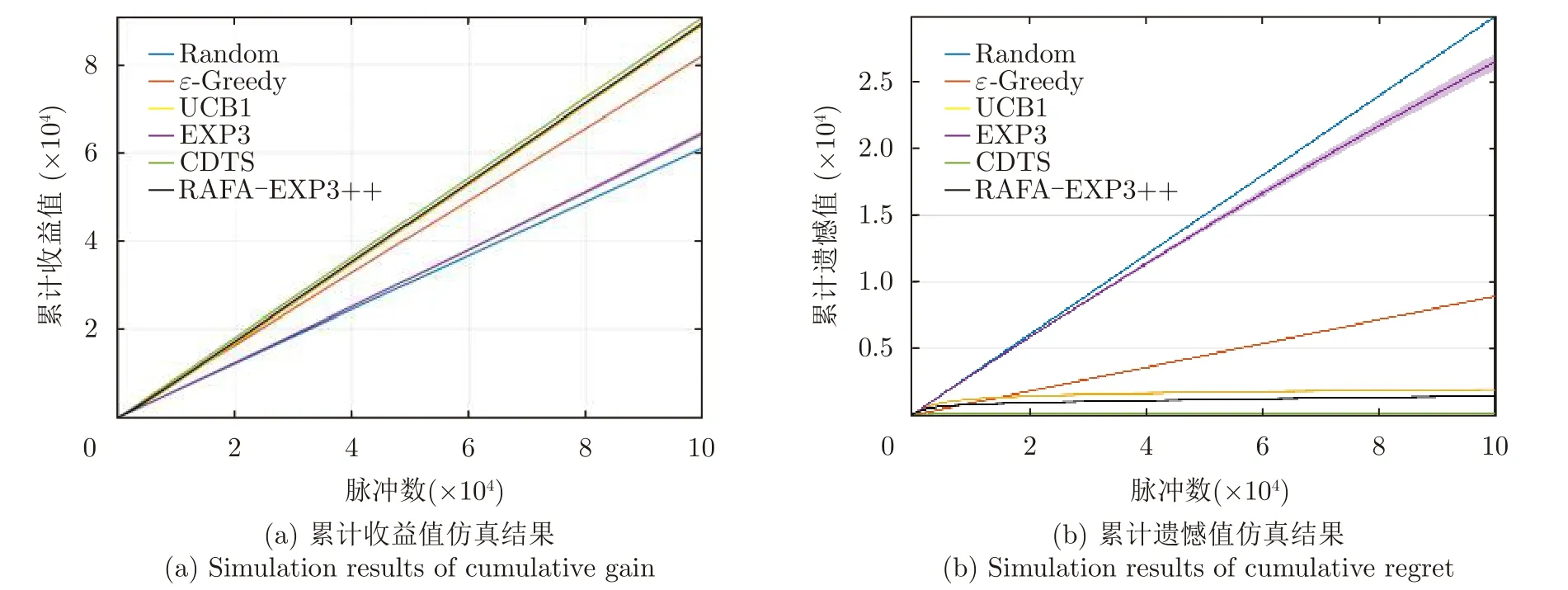
圖4 無干擾環境下所提算法的性能對比圖Fig.4 Comparison plots of the performance of the proposed algorithm in no jamming environment

下面驗證固定干擾策略的干擾場景下本文所提方法的性能。假設干擾機的干擾策略為干擾SNR最高的5個頻率通道，且不隨時間改變。從圖5可以看出，約有15%的發射信號選擇了SINR最高的頻率通道4，同時，由于頻率通道4與頻率通道15的SINR相近，因此約13%的發射信號選擇了頻率通道1。對于受到干擾的頻率通道，選擇概率均在0.1%以下，可以有效避開干擾。從圖6可以看出，本文所提方法在固定干擾策略的干擾場景下仍具有較低的遺憾值，與UCB1算法和CDTS算法性能相近，與EXP3算法相比遺憾值降低約50%。可以看出，在無干擾場景下本文所提方法優于EXP3算法和隨機捷變策略。

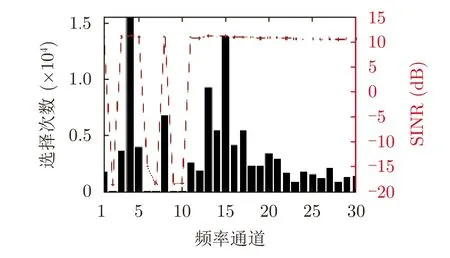
圖5 固定干擾策略環境下頻率通道選擇次數與SINRFig.5 Frequency channel selection times and SINR in the fixed jamming strategy environment

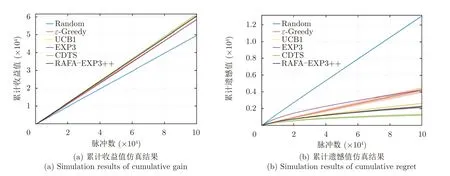
圖6 固定干擾策略場景下所提算法的性能對比圖Fig.6 Comparison plots of the performance of the proposed algorithm in fixed jamming strategy environment

從本節仿真實驗結果可以看出，本文所提方法與隨機性MAB問題中常用的UCB1算法性能相近，優于隨機捷變策略以及EXP3算法，與理論分析相同。我們注意到，與無干擾環境相比，固定干擾策略環境下本算法的累計遺憾值有所提高，這是因為當頻率通道損失期望差Δ變小時，選擇次優頻率通道的次數會增加，導致遺憾值變大，與理論分析相符合。由于最優頻率通道與次優頻率通道的期望獎勵值相近，因此，增加選擇次優頻率通道的次數不會大幅降低雷達的探測性能。

4.3 非自適應干擾場景仿真結果及分析

在本節將驗證本文所提方法在非自適應干擾場景中的性能，干擾場景設置如下。假設非自適應干擾場景中存在一掃頻式干擾機和阻塞式干擾機。當雷達探測過程開始時，阻塞式干擾機開始對雷達工作全頻段進行阻塞式干擾，此時干擾環境的SINR如圖7所示。0.1 s之后掃頻式干擾機開啟，并以固定的干擾功率掃描雷達的工作頻段，掃頻式干擾機的干擾策略參數如表4所示，其他參數見表3。可以看出，無論掃頻式干擾機還是阻塞式干擾機，其干擾策略都與雷達的頻率通道選擇策略無關。

表4 掃頻式干擾參數設置Tab.4 Parameter setting of sweeping frequency jamming

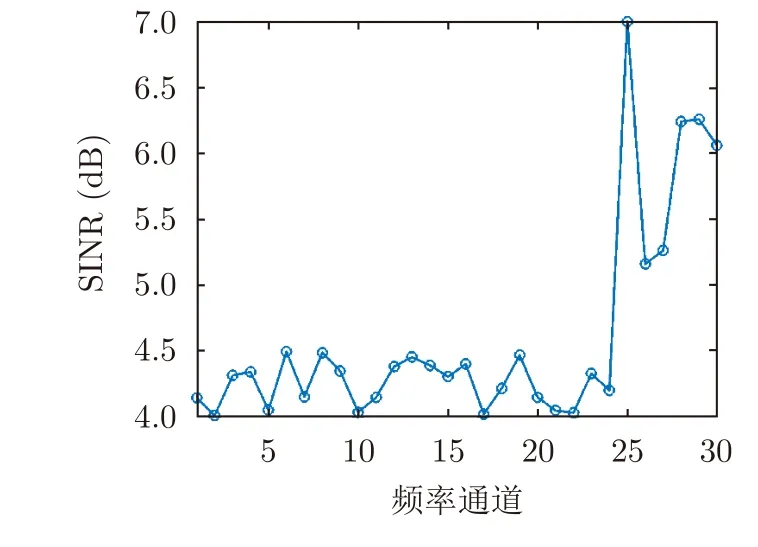
圖7 阻塞式壓制干擾下的SINRFig.7 SINR under blocking suppression jamming

表5統計了在該場景下的雷達檢測到目標的次數。圖8展示了非自適應干擾場景下所提算法的性能對比，可以看出，UCB1算法和CDTS算法僅與隨機捷變策略的性能相當，這說明了隨機性MAB問題假設下提出的算法并不能很好地應用于對抗性MAB問題中。同時，我們注意到UCB1算法和CDTS算法的方差較大，在非自適應干擾場景中存在著不穩定的缺點。而本文所提方法具有與EXP3算法相近的遺憾和收益性能，且算法的方差較小。如表5所示，本文方法與EXP3算法檢測到目標的概率達到73%，ε-Greedy算法達到67%，而CDTS算法和UCB1算法僅與隨機捷變策略的性能相當，僅在55%左右。可以看出，本文方法可以在非自適應干擾場景中有效提升雷達的探測性能。

表5 非自適應干擾場景中檢測到目標的次數Tab.5 The number of detected targets in non-adaptive jamming scene

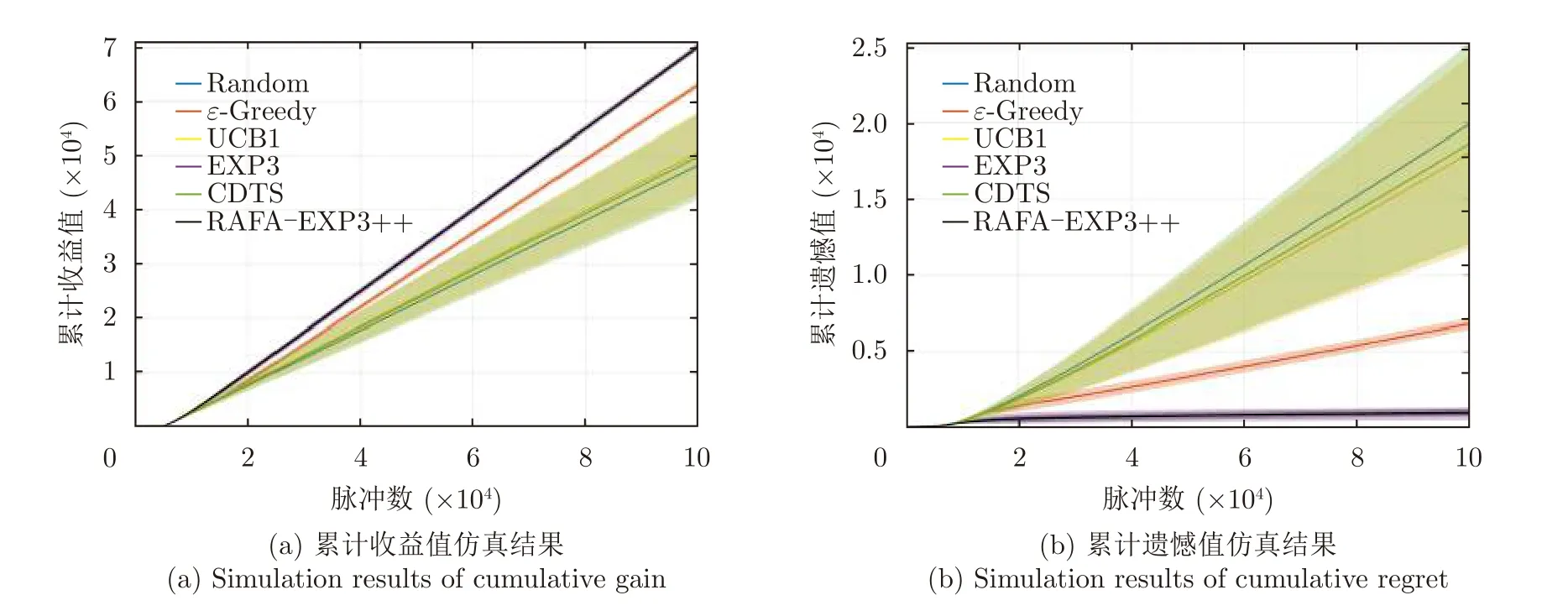
圖8 非自適應干擾場景中所提算法的性能對比圖Fig.8 Comparison plots of the performance of the proposed algorithm in non-adaptive jamming scene

4.4 自適應干擾場景仿真結果及分析

本節將驗證本文所提方法在自適應干擾場景中的性能，干擾場景設置如下。假設初始時自適應干擾場景中存在一自適應干擾機和阻塞式干擾機。其中，阻塞式干擾機的參數與4.3節相同，0.1 s后自適應干擾機開啟工作。如前文所述，本文考慮以1-記憶的自適應干擾機，即干擾信號的中心頻率為雷達的前一個發射頻率，假設干擾機的干擾帶寬為200 MHz，其他參數見表3，可以看出，干擾機的干擾策略與雷達的發射策略有關。

如圖9所示，本文所提方法仍可以獲得與EXP3算法相近的遺憾和收益性能，優于UCB1算法和CDTS算法。對比圖8(a)與圖9(a)可以看出，UCB1算法的收益性能下降最大，這是因為由UCB1算法計算出的發射策略為確定性策略，即在每次頻率通道選擇時，UCB1算法會計算出唯一的發射頻率通道。而CDTS算法、EXP3算法以及本文所提方法計算出的發射策略為隨機策略，在每次頻率通道選擇時，算法并不會指定唯一的頻率通道，而是給出每個頻率通道的選擇概率，然后依概率選擇當前的發射頻率通道，這樣可以提高自適應干擾機對雷達發射頻率通道的預測難度，從而提高雷達對抗性能。我們注意到，相較于非自適應干擾場景，雖然干擾機的干擾功率和干擾帶寬都相同，但由于干擾機的干擾策略與雷達發射策略相關，算法的性能會大幅下降，這與理論分析一致。

圖9 自適應干擾場景下所提算法的性能對比圖Fig.9 Comparison plots of the performance of the proposed algorithm in adaptive jamming scene

表6統計了在該場景下的雷達探測到目標的次數，本文所提方法和EXP3算法檢測到目標的概率約為55%，隨機捷變策略約為54%，CDTS算法約為33%，UCB1算法和ε-Greedy算法均在30%以下。由式(11)可知，本文所提方法中各頻率通道的選擇概率與該頻率通道的權重值呈正相關，由式(13)可知各頻率通道的權重值為各頻率通道累計損失估計值的負指數，對于累計損失值越小的頻率通道，權重值越高，具有更大的被選擇概率。因此，雖然本文所提方法與隨機捷變策略所檢測到目標的次數相近，但本文所提方法會以更大概率選擇到高SINR的頻率通道，可以提升雷達目標識別、跟蹤等功能的性能，故本文所提方法可以提升雷達在自適應干擾場景下的性能。

表6 自適應干擾場景下檢測到目標的次數Tab.6 The number of detected targets in adaptive jamming scene

5 結語

針對噪聲壓制干擾背景下的頻率捷變雷達探測問題，本文提出一種基于多臂賭博機的頻率捷變雷達在線決策方法。本文根據干擾機的策略特征，將壓制干擾場景分為靜態干擾場景、非自適應干擾場景以及自適應干擾場景，以雷達檢測概率為獎勵函數，設計了RAFA-EXP3++算法。理論分析和仿真結果表明，與隨機捷變策略和經典方法相比，本文所提的方法具有更強的靈活性，可適應全部3類干擾場景；且在靜態干擾場景中，本文所提方法可以獲得與UCB1相近的性能，在非自適應干擾場景和自適應干擾場景中，可以獲得與EXP3算法相近的性能。綜上，本文所提方法無需干擾環境的先驗信息和離線訓練過程，可以滿足雷達在噪聲壓制式干擾場景下的在線頻率捷變需求，在多種干擾場景下均能夠有效提升頻率捷變雷達的抗干擾和目標檢測性能。

利益沖突所有作者均聲明不存在利益沖突

Conflict of Interests The authors declare that there is no conflict of interests