直流網光伏系統多時間尺度調度算法
葉清泉,倪佳華,吳旭光,陳偉,吳明啟,項基
(1.國網浙江省電力有限公司平陽縣供電公司,浙江省溫州市 325400;2.浙江大學電氣工程學院,杭州市 310015;3.平陽縣昌泰電力實業有限公司,浙江省溫州市 325400;4.浙江大學工程師學院,杭州市 310027)
0 引 言
電網調度歷來是電網運營的重要組成部分,科學的調度能降低電網運營成本、改善電能質量,提升經濟效益[1-4]。光伏低滲透率情況下,光伏一般以最大功率模式運行,電網調度延續傳統的模式,通過調度儲能和燃料發電機來消納光伏的不確定性波動并優化運營成本[5-7]。
隨著光伏滲透率的增加,電網消納光伏波動的成本也隨之增長,光伏的最大功率運行模式已難以為繼,電網調度開始將光伏作為一種容量可變的電源納入調度范疇[8-10]。文獻[11]建立了包含多種電源類型的混合動態經濟排放調度優化模型,并通過增強的蛾火優化算法求解。文獻[12]提出了光伏啟停和出力優化的混合整數非線性模型,利用正則化和半正定松弛技術將該模型松弛為凸優化問題后求解最優值。文獻[13]提出了一種多能合作博弈優化模型,采用均衡度對比各主體收益,通過智能優化算法求解最優調度量,以求達到各主體的收益分配公平性。文獻[14]提出了負荷跟蹤、功率平滑兩種出力模式的調度模型,利用非支配排序遺傳算法和層次分析法確定最優調度方案。但是,這些文獻都是以預測后得到的光伏容量為基礎,從潮流優化或能量平衡的角度利用不同工具求解光伏等新能源接入下的多目標最優問題,沒有考慮光伏出力的不確定性。
為了減小光伏不確定性波動帶來的影響,提升電網電能質量,學者們研究如何把光伏不確定性納入調度考量。文獻[15]提出了基于機會約束的電網動態經濟調度模型,將光伏的出力預測誤差用隨機變量表示,把機會約束轉化為確定性等價類,最后用改進的粒子群優化算法求解。文獻[16]提出了基于電源分類的兩步式優化調度,首先用三階混合高斯分布量化光伏可用容量預測誤差,用蒙特卡洛法估計光伏不確定性的成本函數期望值和方差;然后用粒子群優化算法在一定量的樣本中找到成本均值最優的調度方案。文獻[17]提出了一種基于區間線性隨機機會約束規劃的優化調度策略,以正態分布函數量化光伏預測誤差,得到機會約束規劃模型,再用常規的規劃方法求解。文獻[18]提出了一種基于模型預測控制的優化調度方法,以光伏出力作為擾動變量,柴油機和儲能作為控制變量,基于未來一段時間已知的擾動變量進行滾動優化和反饋矯正,以保證調度結果的魯棒和抗擾性。文獻[19]提出了一種多目標魯棒優化調度方案,對光伏的不確定性做區間估計代入魯棒優化模型,以兼顧系統的靈活性和穩定性。這些文獻都從數學角度對光伏出力的不確定性進行了量化建模,以此刻畫出力不確定性對整體調度的影響。但是,這些文獻都提前對光伏不確定性波動做出了調整,以減小未來發生光伏波動時的影響。此類方法犧牲了當前時刻下的最優調度性能以彌補未來的不確定性影響,并且無法實時響應光伏的功率偏差。
有學者通過對模型或算法的訓練,使光伏系統輸出自適應光伏的不確定性波動。文獻[8]定義了一個參與因子用以刻畫調度周期間光伏對指令的跟隨程度,以此動態調整下一個周期的參與度,減少不確定性帶來的影響。文獻[20]提出了一種基于神經網絡的調度方案,利用歷史數據訓練神經網絡以提取光伏不確定性特征,在調度中依據預測的波動特性進行提前響應而增強系統穩定性和經濟性。文獻[21]提出了一種基于自適應約束隨機模型預測控制的調度策略,光伏的不確定性可以根據違規水平與期望水平的實際偏差概率以及偏差概率的當前變化率自適應地收緊或放松約束。文獻[22]提出了一種基于深度強化學習的自適應不確定性調度方法,引入深度強化學習中深度確定性策略梯度算法,通過訓練完成的模型自適應光伏隨機波動,避免了對復雜不確定性的建模。然而,光伏出力的隨機性特征是難以用數學模型精確量化和提取的,所以上述方法在實際使用過程中對光伏功率偏差的應對效果是無法保證的。
綜上,光伏系統經濟調度的相關研究中,已有調度方法沒有實時精確處理光伏不確定性帶來的功率缺額問題。當前研究對調度中光伏不確定性的處理方法主要分為兩類:量化和特征化。量化,就是用經典概率函數或可縮放的擾動變量描述光伏不確定性輸出功率,以此得到帶隨機變量的潮流優化模型,然后利用各種求解工具求解。特征化,就是對歷史光伏波動特征進行學習和提取,在算法運行中可以動態地自適應調整光伏的調度,避免了對復雜不確定性的建模。當前在調度中對光伏不確定性的處理思路是通過對不確定性的預估,提前預留一定的備用功率,以此減少不確定性波動發生時的負面影響。但是,光伏的隨機性和間斷性是難以被準確量化和度量的,所以在調度間隙還是會發生光伏缺電現象,由此惡化電能質量。雖然提高調度頻率可以縮短調度間隔,以實現對光伏更及時的調度,但是這無疑會增加調度中心的計算負擔,尤其在大規模電網中,調度周期還會受信息傳輸和處理速度的制約。因此,當前的研究空白在于缺乏一種低負擔的方式直接實時響應光伏的調度功率偏差問題。
本文提出了一種多時間尺度的光伏系統調度策略,以實現光伏熱備用的經濟高效調度。不同于傳統的在集中式調度算法對光伏的不確定性進行數學建模,所提調度方法引入了一致性分布式調度配合集中式調度方法。所提調度算法在不同時間尺度整合了集中式調度和分布式調度算法的優勢:在長時間下的集中式調度算法,可以根據全局信息實現全局優化;在短時間尺度下的分布式調度算法,可以根據光伏電源相鄰節點間的信息實時調度備用功率。所提調度算法無需對光伏輸出的不確定性進行復雜建模,可以實時響應光伏不確定性波動帶來的功率輸出偏差,又保證了全局最優調度。
本文將首先分析光伏在不同天氣條件下的出力特征,再對傳統集中式調度方法及其存在問題進行闡述,然后介紹本文所提的多時間尺度調度方法,最后在IEEE 5節點和IEEE 14節點系統上測試所提算法的性能。
1 光伏在不同天氣條件下的出力特征
光伏出力受到環境的影響(輻照度、溫度等),具有隨機性和不確定性。如圖1所示,分別為額定容量1 kW的光伏面板在杭州晴朗和多云天氣下的最大出力變化曲線。在晴朗天氣下,如圖1 (a)所示,光伏出力相對穩定,其可用容量呈現鐘型分布。圖1 (b)在20 min內展示其可用容量,光伏容量變化很小,波動在10 W以內。在多云天氣下,如圖1 (c)所示,陽光受不確定性云朵影響,其光照強度存在隨機波動,導致24 h內的光伏可用容量曲線也存在隨機和不確定性波動。圖1 (d)同樣為20 min內的容量變化曲線,其在20 min內的可用容量波動高達220 W。
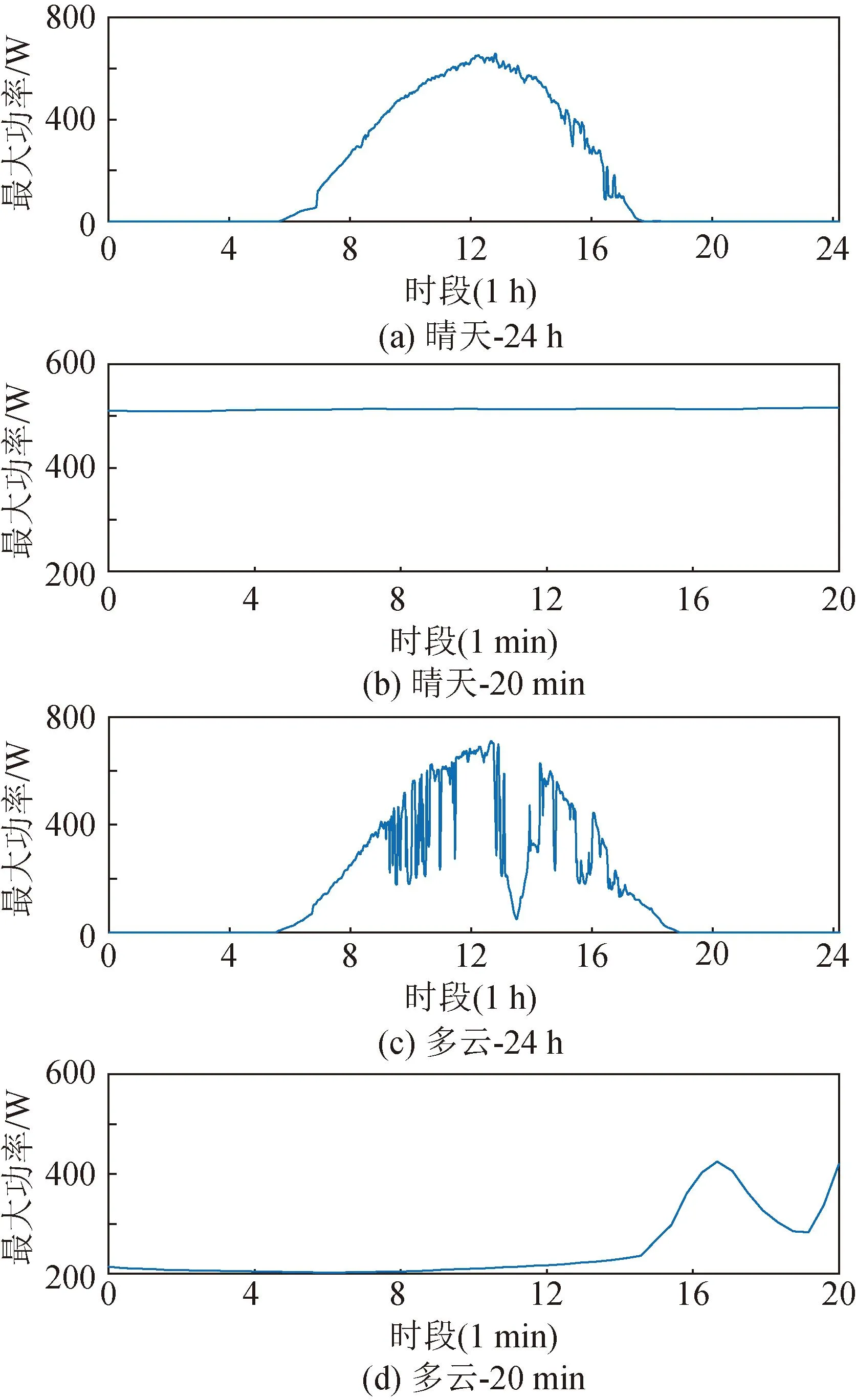
圖1 同一光伏面板在不同天氣情況下的出力Fig.1 A PV panel’s maximum power under different weather condition
2 傳統調度算法及其存在問題
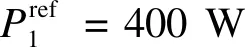
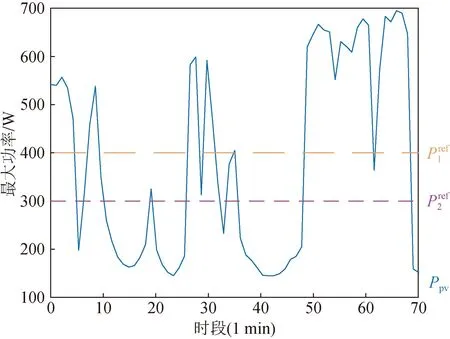
圖2 不同功率輸出參考值下的交互曲線Fig.2 The interaction curves with different power references
2.1 傳統調度算法
在傳統發電機為主體的配電網中,為了使得運行成本最小,其調度優化目標一般為發電成本最小:
(1)
式中:Pg是發電機輸出有功功率矩陣;G為發電機集合;Pg,i為第i臺發電機的輸出有功功率;c2,i,c1,i,c0,i為發電成本系數。
或者網損最小:
(2)
式中:I是支路電流矩陣;L為支路集合;Imn為支路mn上的電流值;Rmn為支路mn的等效阻抗。
從上面兩式可知,傳統的調度算法本質上是在滿足負荷需求的前提下,盡可能減少發電機的燃料消耗成本和線路損耗。但是,當電源由光伏系統構成時,情況有所不同。光伏,作為一種新能源電源,其安裝完成后,發電成本是忽略不計的。而且,從發電用戶側考慮,總是希望其發得越多越好,以提升售電收益,所以光伏的調度會從其熱備成本和節點電壓偏移角度考慮,調度優化目標為:
minf=cψΨ(I)+cφΦ(Pc)+cγY(V)
(3)
式中:cψ≥0,cφ≥0,cγ≥0為權重系數;Ψ(I) 為線損函數;Φ(Pc) 為光伏備用功率函數;Y(V) 為節點電壓相關函數,三者的具體表達式如下:
1)線損函數:網絡中的功率損耗。
(4)
2)功率熱備函數:光伏功率熱備帶來的成本。
(5)
式中:H為光伏集合;ah,bh為成本系數;Pc,h為第h臺光伏電源的備用功率。
3)電壓偏移函數:各節點電壓偏移平均值的程度。
(6)
式中:N為節點集合;n為節點個數;Vi為節點i的電壓。
2.2 問題描述
對比式(2)和式(3)可知,后者增加了備用功率成本和電壓偏移代價函數,但是仍然存在兩個問題:其一,網損最小和熱備成本最小的目標是矛盾的,在負荷一定的情況下,備用功率等于可用容量減去負荷,要減小備用功率,唯一的途徑就是增加網損,顯然對于電網運營方,即購電方,是不能接受的;其二,調度指令往往是基于當前時刻光伏的可用功率,在調度指令更新的時間間隔內,光伏的可用容量是會隨著環境變化而發生不確定波動的,光伏出力的優化沒能考慮實際可用容量不確定變化帶來的影響。如圖3 (a)所示,紅色為調度指令,每10 min根據當前光伏的可用功率更新一次,但是受光伏出力不確定性的影響,在下一次調度指令更新之前,可用功率可能小于調度指令,如陰影部分所示。有一種自然的方案就是縮短調度指令更新間隔,如圖3 (b)所示,當調度指令更新時間間隔從10 min縮短到5 min,在同樣的光照條件下,光伏系統發生功率偏差的時間有所減少,但是越高的調度指令更新頻率,意味著越多的數據傳輸和處理量,尤其是在節點眾多的大規模網絡中,對于中央處理器是一個不小的負擔。
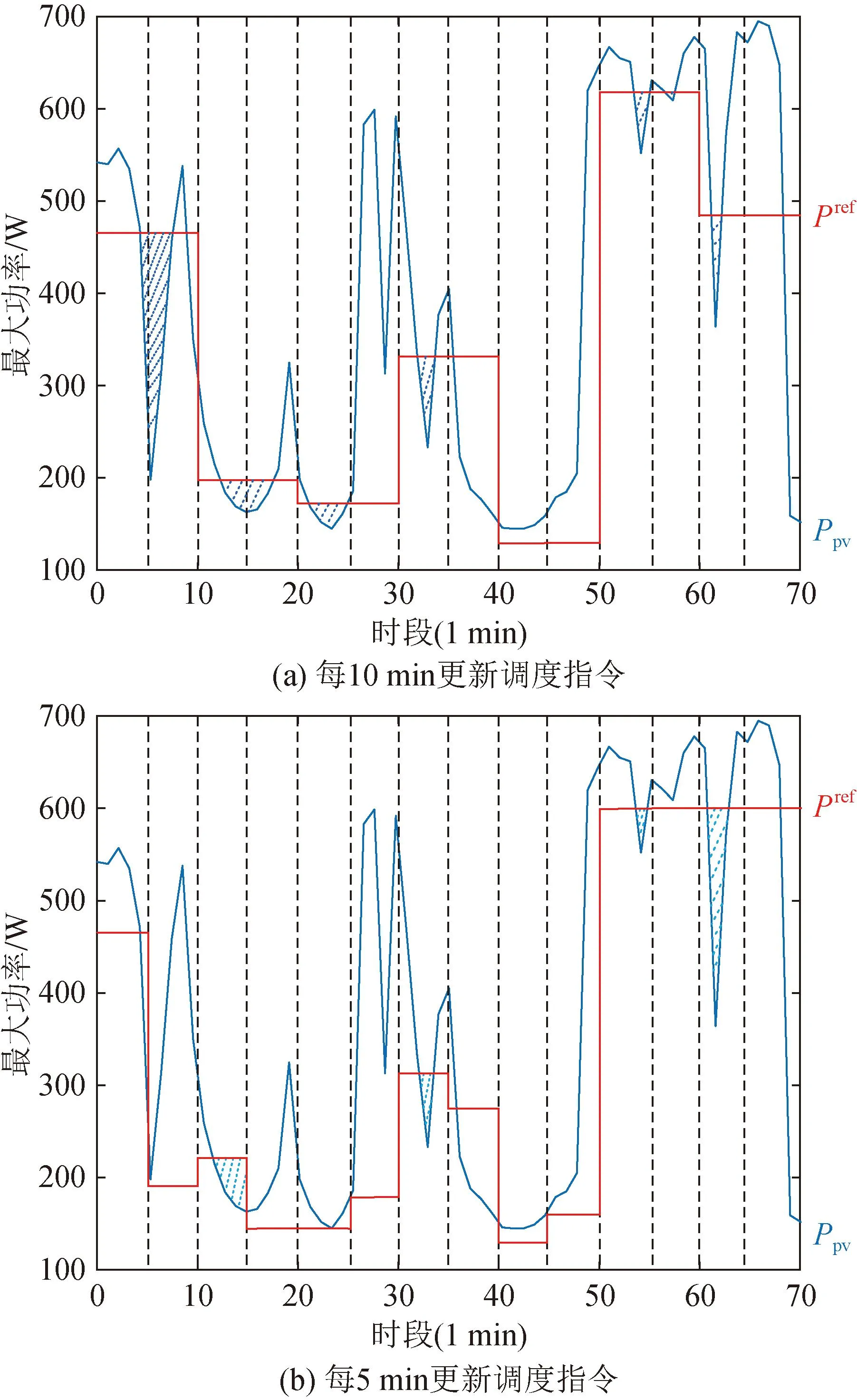
圖3 調度指令下的交互曲線Fig.3 The interaction curves with different dispatching orders
3 所提調度算法
為了解決集中式調度算法更新頻率和計算負擔之間的矛盾,本文提出了多時間尺度的調度方案:上層是集中式的潮流優化調度方法,以滿足網損和節點電壓要求;下層是分布式光伏熱備調度方法,以解決光伏調度功率偏差問題。兩者執行的頻次和信息交互方式如圖4所示,圖4(a)中紅色方塊為集中式調度執行時間,藍色方塊為分布式調度執行時間,由圖可見,分布式調度的時間間隔更短其執行頻率更高;圖4(b)中紅色虛線為集中式調度的信號傳輸線,藍色實線為分布式調度的信號傳輸線。因為集中式調度收集各節點的負荷和容量信息,結合網絡拓撲進行全局優化,因數據量一般較大,指令更新間隔較長頻率較低,而分布式調度算法只運行在各節點本地,和相鄰節點進行信息交換,指令更新間隔較短頻率較高。
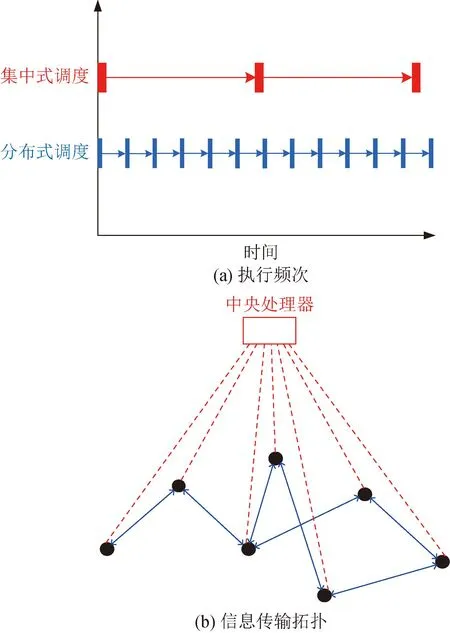
圖4 集中式和分布式調度邏輯Fig.4 Logic of center dispatching and distribute dispatching
3.1 上層集中式調度算法
本文從電網運營者的角度調度光伏輸出功率,所以無需考慮光伏熱備成本,上層調度優化算法以網損最小和電壓偏移最小為目標,其目標函數如下:
(7)
式中:V為節點電壓矩陣。
根據圖5所示的支路模型,可建立如下約束:
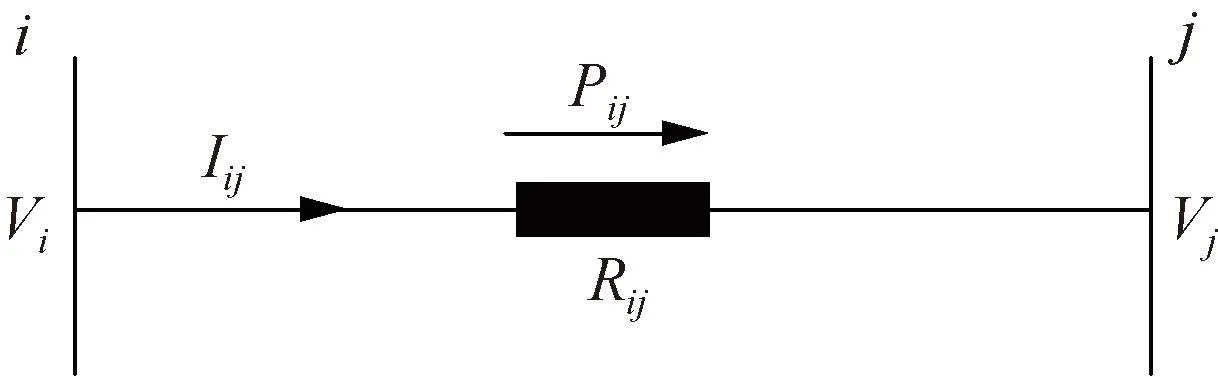
圖5 支路模型Fig.5 Branch model
1)功率平衡約束。
(8)
(9)
(10)
式中:Pg,i是i節點處光伏電源的輸出功率;Pd,i是i節點處負荷的功率;E+={(i,j)|i
2)節點電壓約束。
(11)

3)光伏約束功率。
(12)
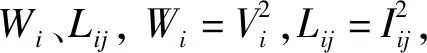
(13)
(14)
電壓約束式(11)變為:
(15)
4)二階錐松弛。
式(14)可以松弛為如下:
(16)
式(16)為二階錐松弛約束,等價于如下約束:
(17)
式(17)可以表示為如下二階錐松弛標準格式:
(18)
5)凸優化模型。
綜上,可以得到如下凸優化模型:
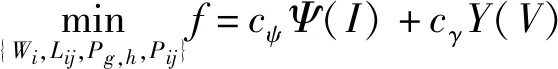
(19)
3.2 下層分布式調度
分布式調度算法的目的是調度光伏備用功率,讓留有多余備用功率的光伏電源根據一定規則調整輸出功率,以補足部分光伏電源因受光照影響而產生的功率偏差。分布式調度算法的指令更新頻率可以在集中式優化調度的10倍以上,各節點只和相鄰節點交換數據,因此無需擔心計算負擔,且適應拓撲多變情況。
1)算法描述。
光伏電源間構成強連通的無向圖G=(N,E),節點個數為n,節點集合N={1,2…,n},邊的集合為E,各節點的度為D={d1,d2…,dn}。Ps,i為節點i處的光伏電源功率偏差,指可用容量不足時,輸出參考功率和可用容量之間的功率差額,即Ps,i=Pref,i-Pmax,i,Pref,i>Pmax,i,容量充足時,功率偏差為零,即Ps,i=0,Pref,i≤Pmax,i;Ps={Ps,1,Ps,2…,Ps,n}為各電源功率偏差構成的向量;Ps(k)為k時刻的功率偏差向量;每兩個時刻的間隔時長為分布式算法執行的周期。
分布式一致性平均算法可表示為:
(20)
式中:P′s(k+1)為中間變量;A=[aij]n×n為權重矩陣;f(·)為自定義運算。
權重矩陣A設計為Metropolis-Hastings矩陣[26],即:
(21)
由于當功率偏差被分配到有多余功率熱備的光伏節點時,功率偏差會被節點消納,此時偏差置零,所以需要對平均后的功率偏差進行處理,運算規則f(·)為:
(22)
即,當前電源輸出功率增加分攤的功率偏差后[Ps,i′(k+1)+Pref,i(k)],若超過可用容量[Ps,i′(k+1)+Pref,i(k)>Pmax,i(k)],則超出部分為其功率偏差,如未超過[Ps,i′(k+1)+Pref,i(k)≤Pmax,i(k)],則分配的功率偏差被全部消納,其功率偏差為零。
2)穩態分析。
上文所提出的分布式一致性平均算法和經典的分布式一致性平均算法有所不同,即每一次運算后會經過f(·)運算調整。但是,其穩態值可以根據經典分布式一致性平均算法的理論推導得到。
首先,回顧經典分布式一致性平均算法的運算規則和穩態值。假設每一次運算結果不經過f(·)函數調整,則可以得到經典分布式一致性平均算法的表達式:
Ps(k+1) =A·Ps(k)
(23)
因為權重矩陣A是雙隨機的(1nA= 1nandAT1n= 1n),根據Perron-Frobenius 原理[26],可得到經典分布式一致性平均算法的穩態值:
(24)
式中:1n為元素全為1的n維向量。
然后,分析所提分布式一致性算法的穩態情況。因為在平均分配過程中,有多余熱備的光伏電源會消納部分功率偏差,所以總的功率偏差是隨時間非增的,即:
(25)
根據光伏可用功率和輸出參考功率之間的關系可得以下兩種情形:
情形1:總的光伏可用功率小于等于總的參考功率之和那么必然在某一個時刻k1,光伏可用熱備均被消耗完畢,此時:
Pref,i(k)=Pmax,i(k),?i∈N且k≥k1
(26)
結合式(20)、(22)和(24),可得:
(27)
情形2:總的光伏可用功率大于總的參考功率之和,那么必然在某個時刻k2,功率缺額被全部消納,此時:
Ps,i(k)=0,?i∈N且k≥k2
(28)
同理可得:
(29)
式中:On是元素均為0的n維向量。
3)算法實現。
上文已經對分布式一致性算法進行了數學描述,為了指導部署和實施,現給出各節點結合集中式調度指令的實現偽代碼,如圖6所示。每一個分布式算法調度周期下,各節點都根據自身的備用功率和周圍節點的功率偏差功率信息更新調度指令Pref,i。
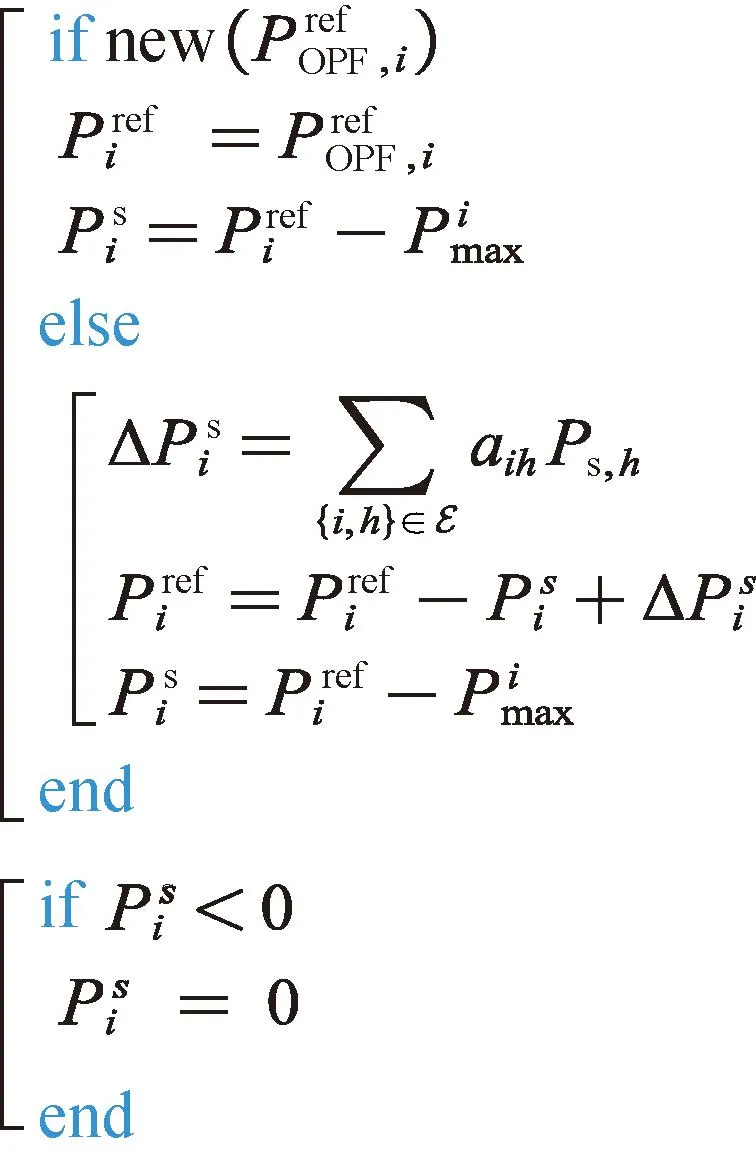
圖6 i節點的調度指令更新偽代碼Fig.6 Dispatching order updating pseudocode of node i
4 仿真案例分析
為了驗證所提算法的有效性,本節設計了3個案例場景進行測試:測試場景1為仿射狀IEEE 5節點拓撲下,不同位置單個電源發生功率偏差時的系統表現;測試場景2為標準IEEE 5節點拓撲下,不同位置單個電源發生功率偏差時的系統表現;測試場景3為標準IEEE 14節點拓撲,在模擬真實光照變化下的系統表現。
4.1 測試場景1:仿射狀IEEE 5 節點拓撲下不同位置單電源容量變化
先測試結構比較簡單的仿射狀IEEE 5節點拓撲下的算法性能表現,拓撲結構如圖7所示。各節點標準條件下光伏電源容量和負荷信息如表1所示。集中式調度算法更新周期為15 min,分布式調度算法更新周期為1 min。我們設置3處光伏電源分別在不同時間發生缺電:

表1 IEEE 5節點拓撲電源和負荷信息Table 1 Generation and load information of IEEE 5-node topology

圖7 仿射狀IEEE 5節點電路拓撲圖Fig.7 Topology diagram of affine IEEE 5-node
在16 min時,節點3處的3號光伏電源容量發生衰減至100 MW;在35 min時,節點2處的2號光伏電源容量發生衰減至150 MW;在50 min時,節點5處的5號光伏電源容量發生衰減至140 MW。
0 min時啟動集中式調度算法,3 min時啟動分布式調度算法。
圖8所示為所提多時間尺度調度算法的系統性能表現。圖8(a)中實線為調度算法給出的各電源功率輸出參考指令Pref,i,虛線為各電源的可用容量Pmax,i;圖8(b)為各節點電壓幅值;圖8(c)為各電源功率偏差Ps,i=Pref,i-Pmax,i;圖8(d)為總功率偏差。
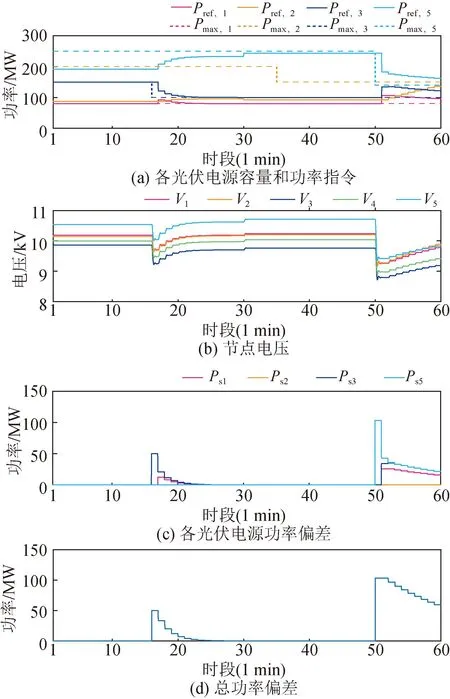
圖8 所提多時間尺度調度算法系統輸出性能Fig.8 System performance of the proposed multi-timescale dispatching algorithm
0 min時,各光伏電源接收集中式調度算法的功率指令,分別輸出80 MW /80 MW,87.46 MW /200 MW,150 MW/150 MW,191.5 MW/250 MW,其中1、3號光伏電源滿發,2、5號光伏電源有裕量。
3 min時分布式調度算法啟動,因無功率偏差,各光伏電源輸出功率保持不變。
16 min時,3號光伏電源發生功率偏差,其可用功率,如圖8 (a)中深藍色曲線所示,從150 MW 降至100 MW,出現功率偏差50 MW,電壓發生跌落,如圖8 (d)所示。同時,分布式算法執行后,各電源的功率偏差得到更新,分別為 0 MW,0 MW,50 MW,0 MW。此時總功率偏差為50 MW,如圖8 (c)所示。
17 min開始,在一致性平均的分布式算法作用下,功率偏差在各節點之間平均,3號光伏電源的功率偏差值逐漸遞減,2號和5號光伏電源的接受部分功率偏差而提高輸出功率,如圖8 (a)中黃色和淺藍色實線所示,因兩者的備用功率充足,參考輸出功率可達到,所以功率偏差一直保持為零。1號電源在18 min時承擔3號電源的12.5 MW功率偏差,因其已經滿發,故其功率偏差為 12.5 MW。19 min開始,1號電源的功率偏差也開始和周圍節點平均,由1號和5號電源消納,故其功率偏差也逐步遞減。同時,各節點電壓也逐步恢復至額定值附近。
25 min時,功率偏差逐步遞減至零,偏差值基本由2號和5號電源消納,此時各電源的輸出功率分別為:80 MW/80 MW,95.56 MW/200 MW,150 MW/150 MW,232.48 MW/250 MW
30 min時,集中式調度算法進行全局優化調度,各光伏電源出力調整為 80 MW/80 MW,92.26 MW/200 MW,100 MW/100 MW,243.18 MW/250 MW。
35 min時,2號光伏電源可用功率下降至150 MW,備用功率仍有富余,故功率輸出保持不變,至到45 min。
上述兩種缺電情況都是在總體可用功率大于負荷的條件下發生,經過分布式算法的若干次迭代后,功率偏差由存在多余功率熱備的電源消納。為了測試算法的穩定性,設計了可用功率小于負荷的情況:
50 min時,5號節點上的光伏電源可用功率減少至140 MW,產生功率偏差103.18 MW,此時電源全部容量為470 MW,負荷500 MW。同時,分布式算法更新各電源功率缺額:0 MW,0 MW,0 MW,103.18 MW。
51 min時,5號電源功率偏差和其相鄰的1號和3號電源平均,由于1號和3號電源已經滿發,功率偏差無法消納,各電源缺額功率分別為:25.81 MW,0 MW,34.41 MW,43.01 MW。
52 min開始,1、3、5號電源功率偏差均逐步減小,2號電源作為1號電源的相鄰節點消納1號電源功率偏差,輸出功率逐步增加。從圖8 (c)可知,總功率偏差逐步減小。直至60 min,受收斂時間所限,各電源之間功率偏差仍未趨于一致,但整體的收斂趨勢是不變的。
圖9所示為傳統的集中式調度算法系統輸出性能,光伏電源輸出功率每隔15 min進行調整,16 min發生光伏功率偏差,雖然由底層下垂控制進行了功率分擔而減緩了電壓跌落,但是各電源逐漸恢復到參考功率,等到30 min時才進行輸出功率調整,50 min處亦然。
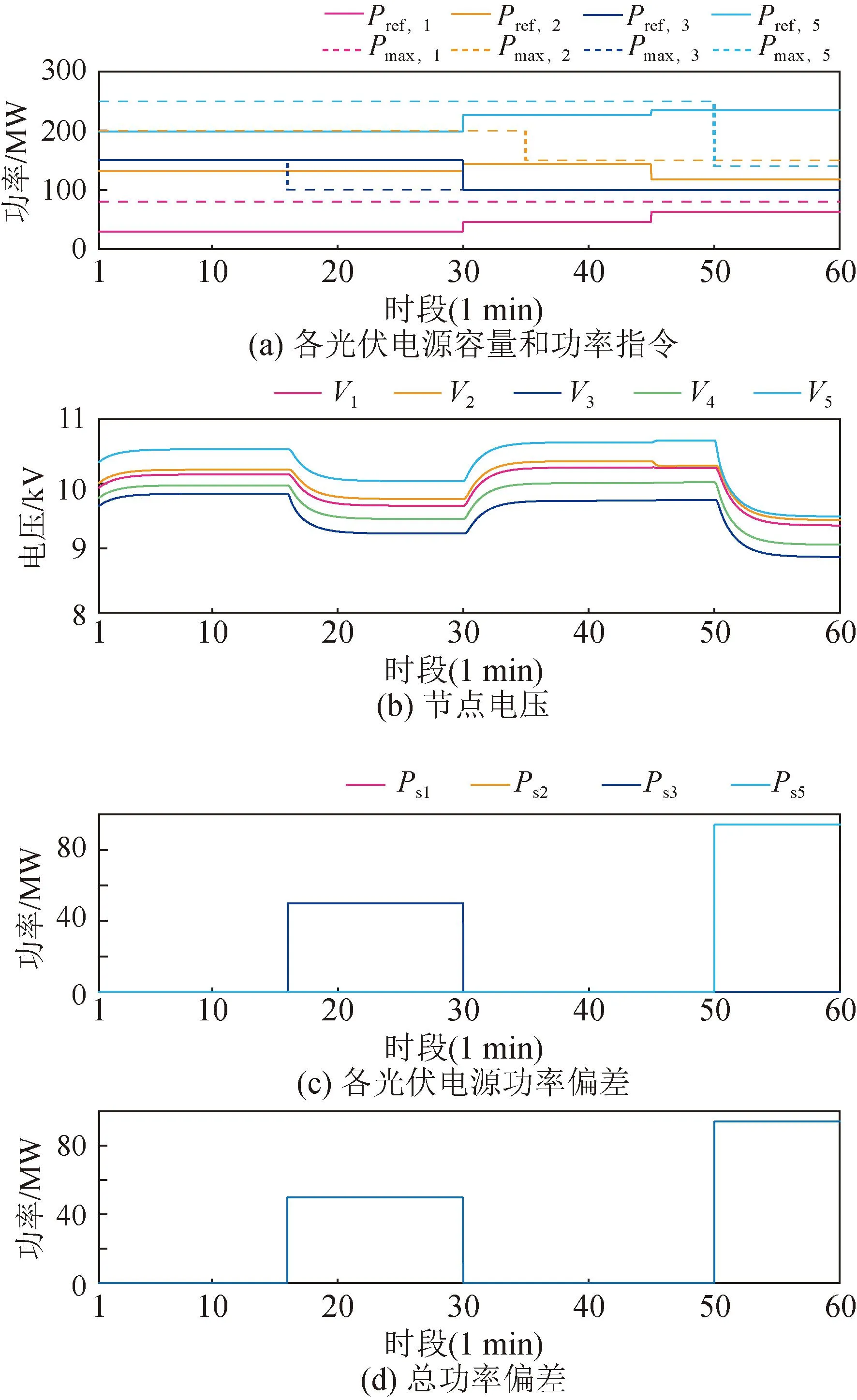
圖9 傳統集中式調度算法系統輸出性能Fig.9 System performance of traditional center dispatching algorithm
4.2 測試場景2:標準IEEE 5 節點拓撲下不同位置單電源容量變化
本小節測試標準IEEE 5節點拓撲下的算法性能,如圖10 所示,與測試場景1相比,網絡拓撲存在環路而變得更為復雜,各節點電源容量和負荷,以及工況變化和測試場景1一致。
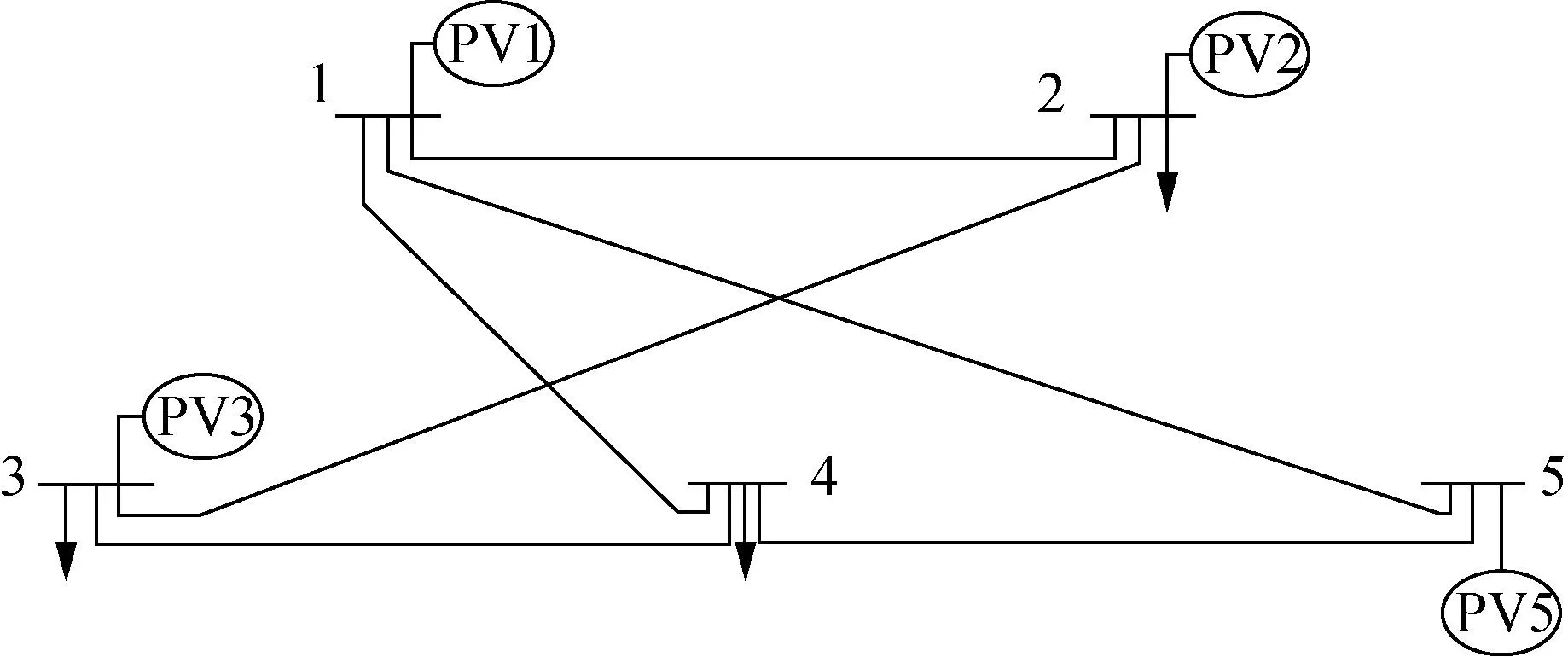
圖10 標準IEEE 5節點電路拓撲圖Fig.10 Topology diagram of standard IEEE 5-node
圖11為所提多時間尺度調度算法的系統性能表現,各子圖含義同上文。0 min時各光伏電源接收集中式調度算法的功率指令,分別輸出25.21 MW /80 MW,191.06 MW /200 MW,150 MW /150 MW,138.23 MW /250 MW,其中3 號光伏電源滿發,其余光伏電源均有裕量。3 min時分布式算法啟動,因沒有發生功率偏差的電源,電源功率指令保持不變。
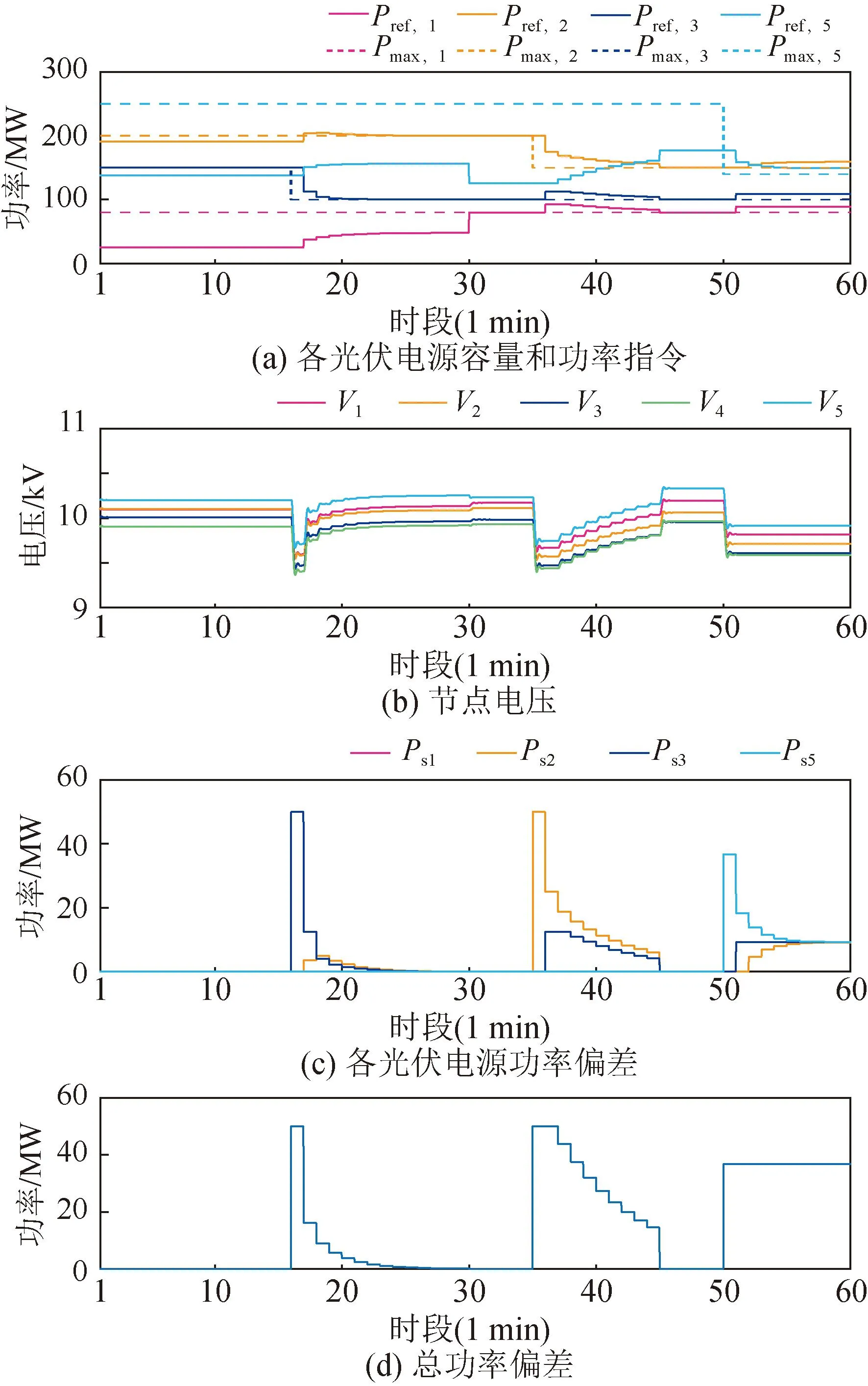
圖11 所提多時間尺度調度算法的系統輸出性能Fig.11 System performance of the proposed multi-timescale dispatching algorithm
16 min時,3號光伏電源發生功率偏差,其可用功率,如圖11 (a)中深藍色曲線所示,從150 MW降至100 MW,出現功率偏差50 MW,電壓發生跌落,如圖11 (d)所示。同時,分布式算法執行后,各電源的功率偏差得到更新,分別為0 MW,0 MW,50 MW,0 MW。此時總功率偏差為50 MW,如圖11 (c)所示。
17 min時,與3號電源的功率缺額與相鄰的1、2、5號電源平均,各電源參考功率分別調整為:37.71 MW /80 MW,203.56 MW /200 MW,112.50 MW /100 MW,150.73 MW /250 MW。此時,3號電源的功率偏差減小為12.5 MW,1、5號電源熱備容量充足而消納分配的功率偏差,2號電源可用容量不足,產生3.56 MW的功率偏差。之后,在分布式一致性平均算法的作用下,2、3號電源的功率偏差逐漸減小由1,5號電源消納。
26 min時,總功率偏差接近零,此時,各電源輸出功率為:47.73 MW /80 MW,200 MW /200 MW,100 MW /100 MW,156.31 MW /250 MW。各節點電壓恢復至額定值10 kV附近。
30 min時,集中式調度算法進行全局優化調度,各光伏電源出力調整為 80 MW /80 MW,200 MW /200 MW,100 MW /100 MW,125.69 MW /250 MW。
35 min時,2號光伏電源可用功率下降至150 MW,產生功率偏差50 MW。分布式算法更新各電源功率缺額,如圖11 (b) 所示,分別為:0 MW,50 MW,0 MW,0 MW。
36 min時,2號電源功率偏差和其相鄰的1號和3號電源平均,由于1號和3號電源已經滿發,功率偏差無法消納,各電源缺額功率分別為:12.5 MW,25 MW,12.5 MW,0 MW。
37 min開始,1、2、3號電源功率偏差均逐步減小,5號電源作為1、3號電源的相鄰節點消納1、3號電源功率偏差,輸出功率逐步增加。從圖11 (c)可知,總功率偏差逐步減小。直至45 min,受收斂時間所限,各電源之間功率偏差仍未趨于一致,此時,進行集中式全局優化,各電源輸出功率調整為:80 MW /80 MW,150 MW /150 MW,100 MW /100 MW,176.24 MW /250 MW。
上述兩種缺電情況都是在總體可用功率大于負荷的條件下發生,經過分布式算法的若干次迭代后,功率偏差由存在多余功率熱備的電源消納。同樣,設計了可用功率小于負荷的情況:
50 min時,5號節點上的光伏電源可用功率減少至140 MW,產生功率偏差36.24 MW,此時所有節點都達到滿發,無法消納功率偏差。
51 min開始,各電源功率偏差趨于一致,在57 min時,基本相等,各電源功率偏差均為9.1 MW左右。此后,保持穩定功率缺額和各電源功率偏差都保持不變。
圖12所示為傳統集中式調度算法在同樣的工況下的系統輸出性能。與所提控制算法相比,各光伏電源輸出功率只在集中式算法運行的時候進行調整,無法實時處理光伏電源的出力缺電情況。在15.5 min,30.5 min和45.5 min,光伏電源產生功率偏差而導致電壓跌落。對比圖11 (c)和圖12 (c)所示各節點電壓的平均偏移程度,傳統的集中式調度算法所示的電能質量更差。

圖12 集中式調度算法的系統輸出性能Fig.12 System performance of traditional center dispatching algorithm
4.3 測試場景3:標準IEEE 14節點系統在模擬真實光照下的系統表現
本小節在標準IEEE 14節點拓撲下進行算法測試,IEEE 14節點網絡拓撲結構如圖13所示,為體現高比例直流網特性,分別在1、2、3、6、8、10號節點接入光伏電源,且光伏裝機總容量大于正常負荷消耗,即由光伏電源承擔全部功率平衡責任。各光伏電源在標準條件下(25 ℃,1000 W/m2)的容量和節點負荷信息如表2所示,光伏系統總容量為1 150 MW,負荷消耗為800 MW。光伏系統間信息傳輸拓撲為完全圖,故分布式算法權重矩陣A=J6/6,J6表示全部為1的6× 6矩陣。

表2 IEEE 14節點系統電源和負荷信息Table 2 Power sources and loads of IEEE 14-node system
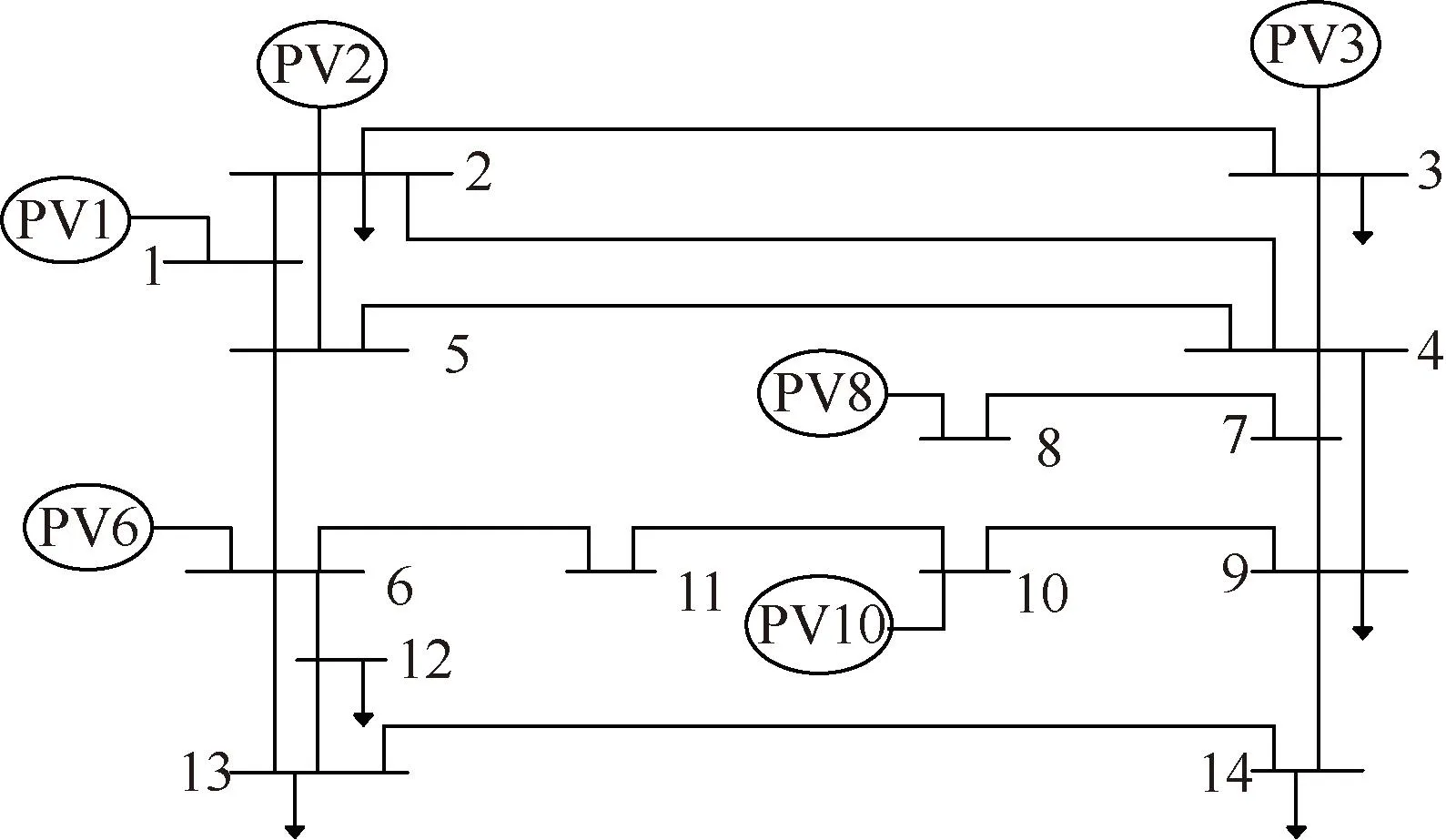
圖13 IEEE 14節點直流網拓撲圖Fig.13 Topology diagram of IEEE 14-node DC grid


圖14 各光伏電源輻照度曲線 Fig.14 The irradiance curves correspond to photovoltaic sources 1,2,3,6,8,and 10
調度算法更新周期和上文一致,集中式調度算法每15 min 運行一次,分布式調度算法每1 min 運行一次。
圖15和圖16分別為所提多時間尺度調度算法和考慮光伏不確定性的集中式調度算法[27]的系統輸出性能。對比兩者結果,從宏觀角度看,因為系統運行時間長,長時間尺度上仍由集中式調度算法主導,故光伏系統輸出曲線和節點電壓波動曲線兩者較為相似。但是,從局部短時間尺度看,特別是光伏容量減少的下行段,兩者有較為明顯的區別,如30 min、70 min、120 min、160 min、240 min 附近,圖15 (b)中,總功率偏差在所提分布式算法的調整下逐漸減小,而圖16 (b)中,兩次集中式調度之間總功率偏差保持不變。為量化比較系統性能,計算了各電源平均功率偏差和各節點的電壓標準差:表3所示為各電源平均功率偏差,從表中可知,所提控制算法作用下的1號和10號光伏電源平均功率偏差比對比算法略高,其余4 臺光伏電源的平均功率偏差均比對比算法更小,尤其是2、3、6號光伏電源的平均功率偏差減小較為明顯;表4所示為各節點電壓標準差,所提多時間尺度調度算法各節點上電壓標準差較對比算法有較大改善,即所提多時間尺度調度算法下系統的節點電壓穩定性更好。
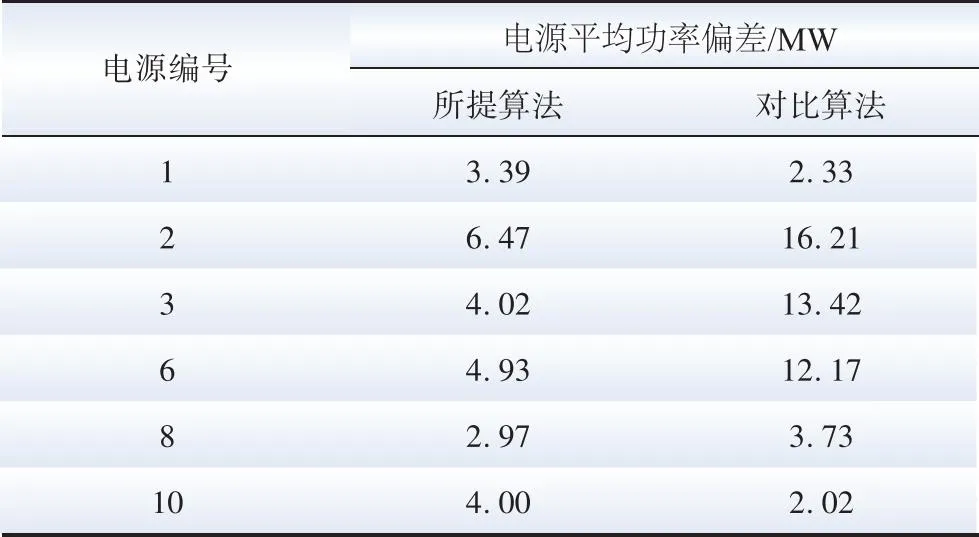
表3 各電源平均功率偏差Table 3 The average power deviation of each power source
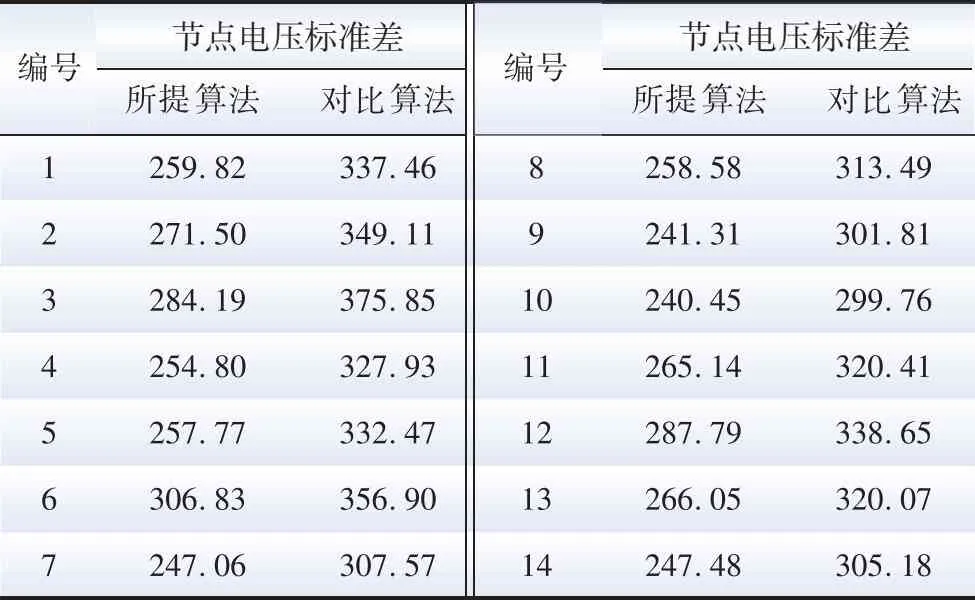
表4 各節點電壓標準差Table 4 The standard deviation of voltage at each node

圖15 所提多時間尺度調度算法在歷史光照場景下的系統性能Fig.15 The system performance of the proposed multi-time scale scheduling algorithm is evaluated under historical irradiance scenarios
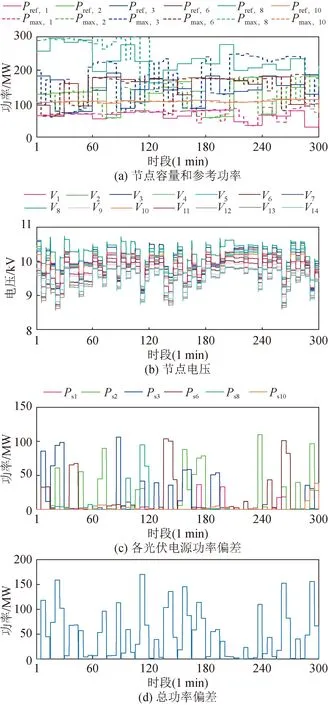
圖16 考慮光伏不確定性的集中式調度算法在歷史光照場景下的系統性能Fig.16 The system performance of centralized scheduling algorithm considering photovoltaic uncertainty is evaluated under historical irradiance scenarios
5 結 論
本文針對光伏系統經濟調度問題提出了一種多時間尺度的調度算法,解決了傳統集中式調度算法在光伏不確定性波動下的調度負擔和調度實時性之間的矛盾。所提多時間尺度調度策略分為兩層:第一層為在長時間尺度下的集中式調度算法,可以根據全局信息實現全局優化;第二層為在短時間尺度上的分布式調度算法,光伏電源根據相鄰節點間的信息調度可用功率。建立了直流網下基于二階錐松弛的全局凸優化模型和光伏系統間信息交換和功率調整規則。最后,在IEEE 5節點系統上進行了單電源和多電源容量變化下的仿真測試,在IEEE 14節點系統上結合歷史光照信息進行了模擬真實光照環境的測試,結果表明所提多時間調度算法提升了光伏系統備用功率的利用效率,減小了各電源的平均功率偏差,而且使節點電壓具有更好的穩定性。

