考慮風速時空分布及機組運行狀態差異的風電場有效慣量估計

李東東,張先明,姚寅,徐波,鞏偉崢

(1.上海電力大學電氣工程學院,上海市 200090;2.國家電網有限公司華東分部,上海市 200120)

0 引 言

隨著能源供應緊缺和環境保護的重視,風力發電依靠成熟的技術和良好的應用前景在電網中的比例逐年增長。以雙饋異步發電機(doubly fed induction generator,DFIG)為代表的風電依靠電力電子器件并入電網,導致機組無法響應系統頻率的變化,降低了系統轉動慣量水平[1-3]。為滿足風電的發展要求以及避免系統頻率穩定性的惡化,應充分挖掘風電機組虛擬慣量響應潛力,當前已有眾多學者針對風機轉子動能控制展開研究,使其具備類似同步機組慣量響應的能力,并類比同步機組搖擺方程對風機慣量水平進行估計。但仍存在以下弊端亟需解決。

其一,風速具有隨機性和不確定性,大型風電場的風速分布差異性顯著。導致DFIG轉子旋轉慣量難以實時評估。當前風場風速預測的方法分為兩類:基于空間相關性和數值天氣預報的機理驅動法[4],基于時間序列、概率模型和機器學習預測的模型驅動法[5-7]。文獻[8]提出計及尾流效應、時延效應的風速相關性分析方法,效率高,但大規模風電場預測精度低。文獻[9]基于大氣數據提出數值天氣預報法,通過數值計算實現場站級別風速預測,而單機計算量過大,實時性較差。對于模型驅動法,文獻[10-14]提出Copula函數風速預測方法,其準確度受模型選取及精度的影響。綜上,本文采用尾流效應分析相鄰機組和混合Copula函數分析任意機組風速相結合的雙驅動風速預測方法。在保證精度的同時顯著提高預測效率,便于后續風機慣量實時在線估計。

其二,風機虛擬慣量支撐能力受外界風速和自身運行狀態影響,其能量來源——轉子動能直接受風速影響。低風速下受轉速下限的約束,僅能提供少量慣量支撐[15],高風速下受電磁功率上限的約束,無法提供足夠的額外有功功率支撐[16]。對此在中高風速下通過減載控制降低功率輸出,不僅使機組具備一次調頻能力,還能改善慣量響應特性[17]。文獻[18-20]考慮不同風速下風機運行狀態的差異,得到各風速區間內的慣量評估表達式。文獻[21]提出減載控制和虛擬慣量結合的方式,能夠有效減小虛擬慣量響應能量輸出,避免轉子失速和頻率二次跌落。但未對減載控制后的風機虛擬慣量特性展開具體研究。對此本文分析不同風速區間減載控制下風機慣量響應特性的變化,并對參與慣量響應的轉子動能進行評估。

其三,DFIG虛擬慣量響應時,轉子轉速不斷下降使其風能捕獲偏離最大功率點跟蹤狀態。捕獲機械功率低于初始值并不斷下降,缺額部分功率由轉子動能補充,這造成了能量的損耗,使轉子動能不能100%參與慣量支撐。對此,風電場慣量評估需針對虛擬慣量動態過程進行具體分析,以修正慣量估計值,對此文獻[22]分析風機慣量響應過程中轉子動能損失以及轉速恢復階段的動態過程,但文章后續聚焦于改進慣量控制策略以減少動能釋放。文獻[23]通過內電勢相位運動方程,推導了異步電機的時變慣量表達式。文獻[24]從機-網特性的視角,基于雙饋風電機組的并網頻率響應模型推導其慣量表征式。文獻[25-28]從能量釋放角度給出DFIG慣量時間常數表征式。以上分析都忽略了風機慣量響應時刻機組運行情況。對此,本文考慮各機組運行狀態差異,對虛擬慣量動態過程進行解析,提出修正后的風電有效慣量估計方法。

綜上,本文提出雙驅動風速預測模型實現風場風速時空分布預測。同時,對于不同運行狀態和不同控制參數下的風機虛擬慣量響應過程進行動態分析,得到風電機組有效慣量表達式。最后,結合風速預測模型實現風電場有效慣量的在線估計,為掌握風電場真實慣量響應水平提供依據。

1 雙驅動風電場風速概率模型

本節采用雙模型驅動方法對風電場風速概率分布展開預測。具體流程見圖1。

圖1 風電場風速概率模型構建流程圖Fig.1 Flow chart of wind farm wind speed probability model construction

風電場通常利用測風塔獲取實時風速數據,測得的風速數據準確度高,能反映風電場整體風能資源大小,為構建風電場風速時空分布模型提供數據支撐。首先,對各臺風機風速數據進行優化處理,并采用k-means聚類法實現風電場的聚類分區[29-31]。對于機群內部,采用尾流效應分析相鄰機組間風速的相關性。對于機群之間,采用混合Copula函數擬合風電場內各機群和測風塔風速的相關性。該模型的特點在于只需輸入測風塔實時量測數據,即可得到各機組實時風速概率分布。

1.1 尾流效應機理

依據空氣動力學原理,下游機組受上游機組尾流遮擋,機端風速降低。這種現象稱為尾流效應。伴隨當前風機設計能力的加強,槳葉半徑越來越大,遮擋面積增加。同時風場逐步朝著大規模級別發展。風場內部尾流效應明顯。在考慮風電場內部風速變化特性時,尾流效應不可忽略,如圖2所示。

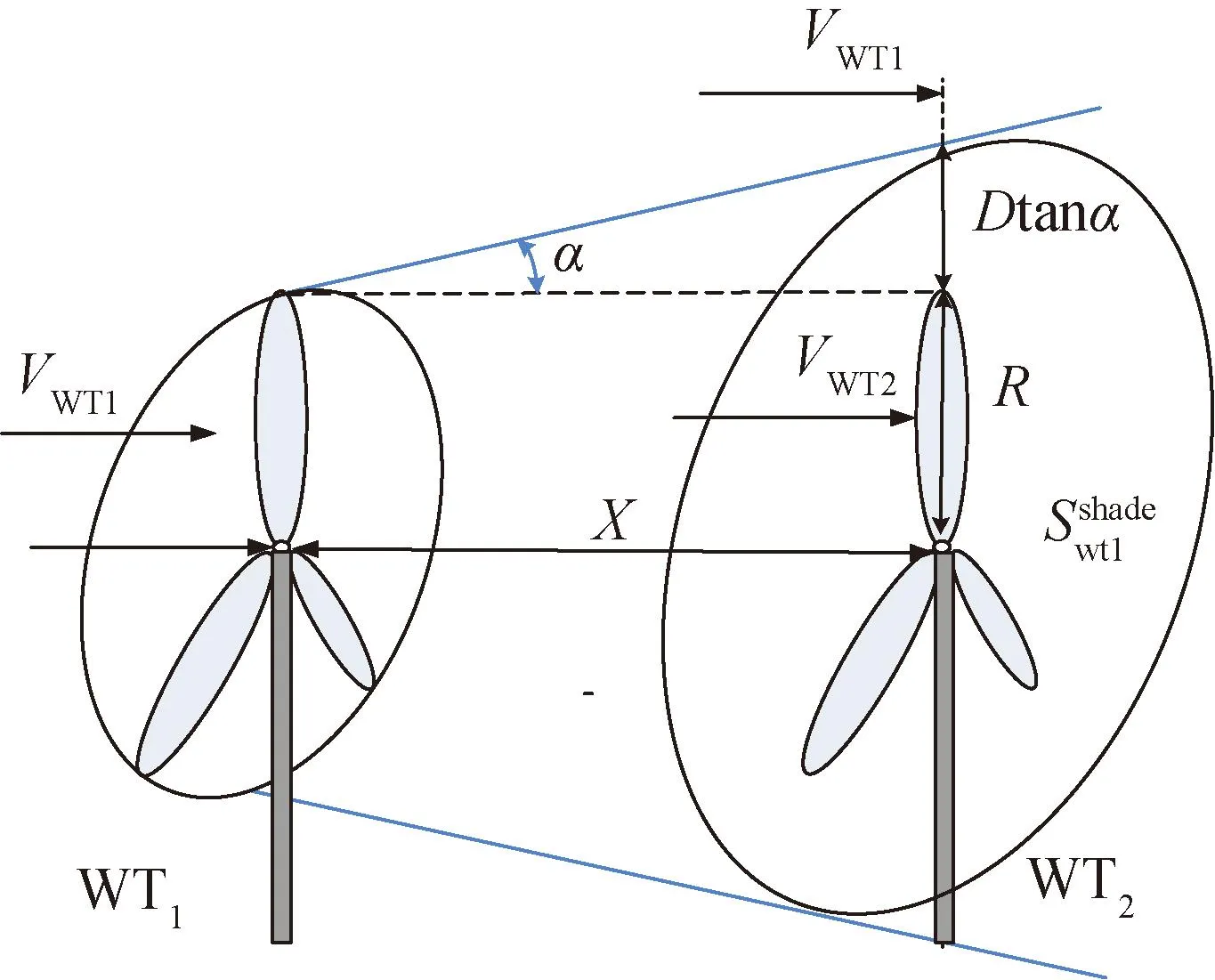
圖2 尾流效應原理圖Fig.2 Schematic diagram of wake effect

式(1)為常規Jensen尾流模型[32]描述上下游機組間風速關聯公式。

(1)

式中:VWT1、VWT2為機組WT1、WT2的機端風速;d為風速下降系數;CT為推力系數;R為葉片半徑;D為兩機組間隔;tanα是尾流常數,其中α為圓錐頂點系數。

圖1中WT2完全處于WT1尾流效應投影范圍內,但在實際運行中,由于風機地理位置以及風向的轉變,大多數風機處于尾流效應部分遮擋的區域,對此,修正后的公式為:

(2)

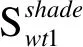
對于上游n′臺機組的尾流效應影響,下游機組j的風速受上游風機尾流效應疊加影響,如式(3)所示。

(3)

式中:Vj0為機組j未受尾流效應的風速。對于機群內部風電機組,采用尾流效應分析風速相關性的準確度較高。然而對于大型風電場,風速尾流效應疊加層次多,對于下游機組的風速擬合準確度較差,對此采用聚類方式實現風電場規模的降維處理,后續通過Copula函數預測各機群風速。

1.2 混合Copula函數

Copula函數可以實現多元隨機變量邊緣密度函數和聯合概率分布函數的連接,能將N個隨機變量的聯合分布分解為N個變量各自的邊緣分布以及一個Copula函數,實現變量隨機性和耦合性的分離,具體分析如下。

設測風塔測量的風速為V1以及各機群中心機組構成的多維風速隨機變量為V2,利用非參數核密度估計法構造邊緣分布函數f(V1)、f(V2),詳細過程見附錄A。若F(V1、V2)為兩處風速變量的聯合分布函數,則存在唯一的Copula函數C(·)將聯合分布函數和邊緣分布函數進行連接。

F(V1,V2)=C[f(V1),f(V2)]

(4)

不同相關性分析采用不同類型Copula函數,常見Copula分類見文獻[10],單一的Copula函數擬合時會出現失真,導致相關性分析誤差過大,對此可將特性不同的Copula函數按式(5)組合,構造混合Copula函數提高風速預測精度。

(5)

式中:m表示Copula函數的種類,一共有M個;φm∈[0,1]為權重系數;θm為描述相關變量之間相關性的相依系數。參數的求解是構造混合Copula函數的關鍵。本文提出利用EM算法進行參數估計,如算法1所示。

算法1 EM法估計混合Copula函數參數輸入:最大迭代次數I,相互獨立的觀測變量X。參數估計步驟:1.對需要估計的參數θ賦初值θ(0),進行EM算法迭代,迭代次數不能超過I。2.E步(期望步):第一輪采用θ(0),后續采用上一次M步求得的θ(t),計算隱變量z的條件概率Q(t)(z(m)|x(m);θ(t))。3.M步(極大步):根據求得的Q值,按下式更新參數θ(t+1)。θ(t+1)=argmax∑i∑z(i)Q(t)i(z(i))logp(x(i),z(i);θ(t))Q(t)i(z(i))(6)4.重復步驟2、3直至結果收斂,收斂依據為更新差值小于閾值ξ或達到最大迭代次數I:(θ(t+1)-θ(t)≤ξ)∪(t=I)(7)輸出:模型參數θ。

混合Copula函數擬合精度高,但是構建過程復雜,為減小算法計算量,僅構建各機群中心機組與測風塔的混合Copula函數。利用求得的混合Copula函數并結合公式(4)、(5)可以得到測風塔風速與中心機組風速聯合概率分布函數F(V1、V2),若已知t時刻測風塔風速為V1-t,則代入公式(4)后可以得到t時刻中心機組的風速概率分布函數f(V2-t)。由此獲得各中心機組風速的概率分布。

綜合上述兩節內容,構建雙驅動風電場風速時空分布概率模型,為各機組有效慣量估計提供數據支撐。

2 風機有效慣量估計

DFIG自身特性導致其慣量估計復雜,一是換流器控制策略決定虛擬慣量支撐功率大小,控制策略的靈活多變導致不能簡單地通過換流器參數來估計慣量水平,二是機組慣量水平受當前外部輸入和自身運行方式的變化而波動,機端風速影響最為顯著。相較于同步機轉子轉速在±5%的范圍變化,DFIG在虛擬慣量響應時轉速變化范圍為0.7～1.2 pu。以上這些特性都導致參與虛擬慣量支撐的能量隨時間劇烈波動,風電場內部慣量空間分布的差異更加明顯。

綜上,從能量角度分析風電機組慣量水平是最佳選擇,以風速為輸入量,通過分析機組運行狀態及其慣量響應過程,求解風機虛擬慣量能量波動。

2.1 DFIG運行特性分析

雙饋風機捕獲風能轉化為機械能,拖動感應電動機旋轉,輸出電磁功率Pe,其中捕獲的機械功率Pm由式(8)決定:

(8)

式中:ρ為空氣密度;CP(λ,β)為風能利用系數,是葉尖速比λ和槳距角β的函數;λ表示葉片末端線速度與風速的比值;ω為轉速;V為風速。

風能利用系數CP與λ、β詳細關系如附錄B所示。槳距角固定不變時,存在唯一的葉尖速比λopt使風能利用系數最大,這種運行狀態稱為最大功率跟蹤(maximum power point tracking,MPPT)。該模式下風機既無功率備用,也無慣量支撐能力。

為使風機具備參與慣量響應和一次調頻的能力。通過轉子動能控制將風機轉子存儲的動能轉化為額外有功支撐。常采用PD型綜合虛擬慣量控制,控制模型見圖3。

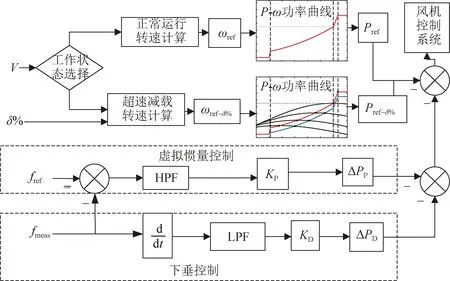
圖3 風機綜合運行控制框圖Fig.3 Fan integrated operation control block diagram

由圖3可知附加虛擬慣量控制的風機輸出電磁功率由式(9)決定:

(9)

式中:Pref為正常運行參考功率;KD、KP為虛擬慣量控制比例系數;fmeas為實測頻率;fref為額定頻率參考值。

為保證頻率數據不受雜波影響,圖3中附加了低通濾波器(low pass filter,LPF)和高通濾波器(high pass filter,HPF)。圖3中風機處于正常工作狀態時,功率曲線按照風速范圍的不同可分為啟動區、MPPT區、恒轉速區和恒功率區。各區間轉速-功率曲線按照公式(8)推導如下:

(10)

式中:k為啟動區的比例系數;kmax為MPPT區的比例系數;Pmax為最大功率;ωmax、ωmin分別為最大、最小轉速。

由圖3可知,除正常運行方式外,可按照預先設置的減載率δ%要求,通過超速減載或槳距角控制實現功率備用。中低風速下,轉子尚未達到額定轉速,通過超速減載控制,使其偏離MPPT運行點,風機轉速增加,輸出電磁功率減小。則減載運行下的葉尖速比δ%可利用式(11)求解:

(1-δ%)·CP(λopt,β)=CP(λδ%,β)

(11)

高風速下,為減小風力的沖擊,機組通過槳距角調節實現功率恒定在最大值,此時轉子轉速達到最大,只能通過進一步調節槳距角大小實現功率的備用。

2.2 考慮機組運行狀態的有效慣量估計

雙饋風機實際參與慣量支撐的過程如圖4所示。虛擬慣量響應過程中,按照用途的不同,存在3部分能量:轉子釋放動能ΔED(作為慣量響應的能量來源)、能量轉化損失ΔELOSS、機械能損失ΔEM。故轉子釋放動能并未全部參與慣量支撐,對此本文定義參與實際慣量支撐的能量為有效慣量ΔEK,如式(12)所示:

圖4 風機慣量響應過程分析Fig.4 Analysis of fan inertia response process

ΔEK=ΔED-ΔEM-ΔELOSS

(12)

雙饋風機慣量響應時,轉子轉速下降釋放動能。結合圖4從外部能量角度分析,轉子釋放動能ΔED約等于電磁功率與機械功率差值關于時間的積分,如式(13)所示。

(13)

(14)

機械能損失ΔEM是雙饋風機異于同步機組的特性。即轉速變化會影響機械功率的捕獲,導致虛擬慣量響應時,捕獲機械能減小,用于補充該部分的能量損失稱之為機械能損失,計算公式如下:

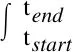
(15)

式中:Pm(t)可由公式(8)展開,與機端風速、風能利用系數相關。慣量響應持續時間一般為秒級,可認為這期間風速維持不變。風能利用系數的變化則復雜的多,對此需進一步求解分析。

以MPPT運行狀態為例,槳距角恒為0。虛擬慣量響應階段轉速變化曲線通過線性擬合可得:

(16)

其中:

(17)

利用式(16)結合公式(8)中轉速和葉尖速比的關系得葉尖速比時變函數如下:

(18)

在槳距角為0的情況下,將葉尖速比時變函數代入到風能利用系數表達式中。

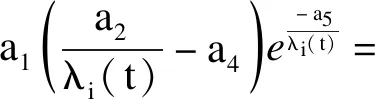
(19)

式中:CP為風能利用系數,是關于時間t和葉尖速比λ、槳距角β的函數;λi是與λ相關的中間系數;α1、α2、α3、α4、α5為相關系數。

由此得到慣量響應階段風能利用系數時變函數。將式(19)代入到式(8)、(12)、(15)可得風機有效慣量展開解析式,見附錄C。可知MPPT運行狀態下有效慣量是關于風速、轉速、捕獲機械功率和慣量響應持續時間的函數。其他運行狀態對有效慣量估計的影響分析如下。

（1）對整條光鏈路進行故障判斷。具體方法為在兩站端連接至繼保裝置處的尾纖頭用光源和光功率計測試。一站端的尾纖頭連接光源發光，另一站端的連接光功率計測試。收發兩條鏈路都要進行檢查測試，檢查鏈路是否暢通，衰耗是否滿足繼保通道的需求。若暢通且衰耗滿足要求，則可認定為光鏈路無任何問題，故障并不在通信專業的運維界面內，流程轉至第（5）步；若不通暢或者衰耗不達標，則需要進行具體故障位置定位，流程轉至第（2）步。

1)正常恒轉速運行狀態,風機脫離MPPT運行,公式(16)不再適用于推導轉速與風速的關系,此時可通過線性擬合的方式解析風速與轉速的關系。

2)正常恒功率運行狀態,通過槳距角調節實現高風速下功率的恒定,不同風速對應不同槳距角。慣量響應時風能捕獲利用系數不僅與葉尖速比有關,還需要獲取槳距角大小,對此需要修正風能利用系數表達式(19),見附錄C。

3)超速減載運行,該運行狀態對有效慣量估計的影響為兩方面,一是捕獲機械功率降低,如圖4中超速減載運行點B1、C1、D1縱坐標與正常運行點B0、C0、D0縱坐標對比,比例系數即為減載率。二是風機轉速增加,轉子動能增加。如圖4中超速減載運行點橫坐標所示。

4)變槳減載運行狀態:捕獲機械功率下降,葉尖速比脫離最優值,槳距角進一步增大。注意,高風速區正常運行時,通過槳距角控制實現功率恒定為最大值,若減載運行也需采用變槳控制,使功率恒定在次最大值,這兩種運行都需要變槳調節實現,但是目標功率不同。

最后,中低風速時,超速減載運行下的機組在慣量響應時,為盡可能釋放轉子動能,會不斷降低轉子轉速直到最小值;而超速減載控制下的機組在參與一次調頻時,為盡可能實現持續的功率支撐,轉速降低到最優轉速,使其工作點由次運行點回歸到最大功率捕獲運行點,持續增加輸出電磁功率以應對功率缺額,本文僅對風機慣量水平展開評估,因此不考慮第二種狀況,超速減載只考慮轉速降低到最小值這種情況。

3 仿真分析

3.1 雙驅動風速預測模型分析

以某風電場38臺機組為例,測量數據為各風機機端風速、轉速及功率,采樣間隔為10 min。各參數設置見附錄D,雙驅動風速預測模型步驟如下。

1)風速邊緣概率分布函數。

風速的隨機性使得其邊緣分布函數難以用常見的分布模型進行匹配,對此本文采用非參數核密度估計法構建風速邊緣概率分布函數,該方法能適應風速復雜的分布特性,結果如圖5所示。

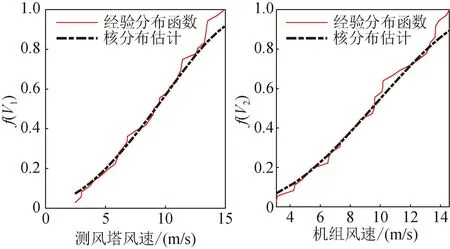
圖5 非參數核密度估計對比分析 Fig.5 Comparative analysis of nonparametric kernel density estimation

2)混合Copula函數的構建。

為確定各類Copula函數對實際風速相關性的擬合效果,需繪制測風塔和機組的風速聯合頻率分布直方圖,如圖6所示。

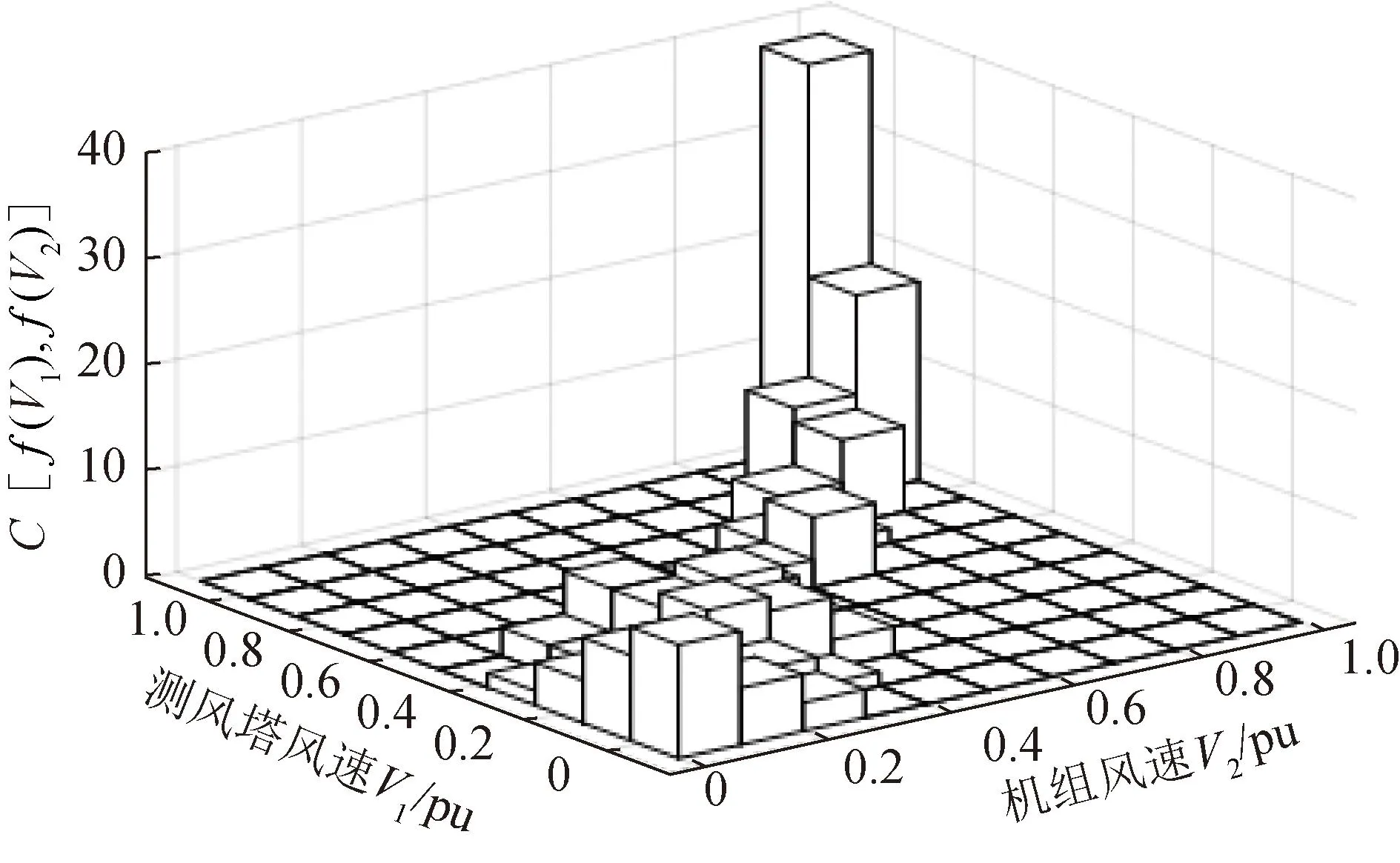
圖6 聯合頻率分布直方圖 Fig.6 Joint frequency distribution histogram

由圖6可知,風速聯合頻率分布主要集中在45°對角線上,表現出明顯的尖峰后尾特性。表明測風塔與機組風速具備等比關系,且在高風速下具備尾部強相關性。據此,采用不同類型Copula函數進行擬合,效果如圖7所示。

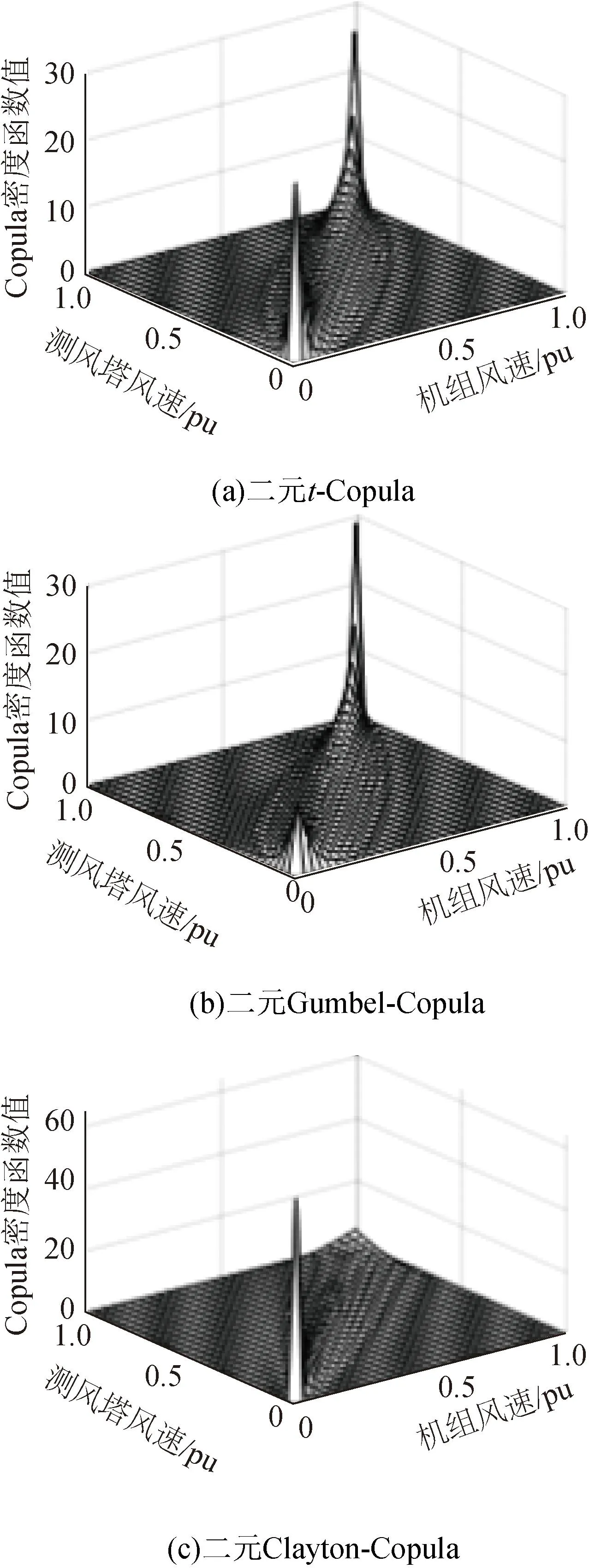
圖7 不同類型Copula函數聯合概率密度圖Fig.7 Joint probability density map of different types of Copula functions

對上述四種典型Copula函數進行組合,利用本文所提EM算法估計混合Copula模型的參數,結果見表1。

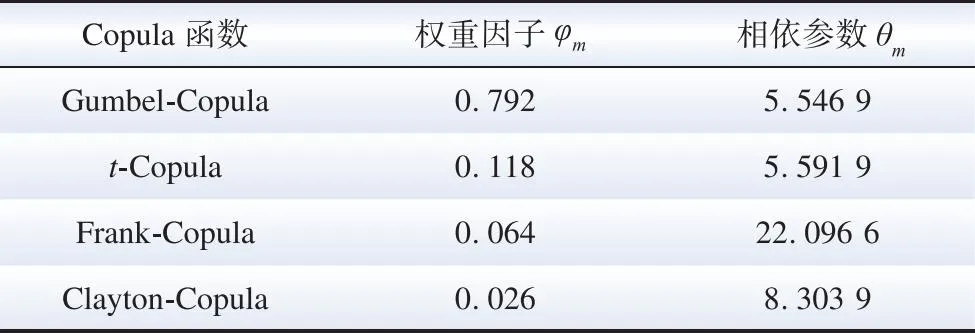
表1 混合Copula函數模型Table 1 Mix the Copula function

將表1中參數值代入公式(5)中得到混合Copula函數公式,擬合結果如圖8所示。

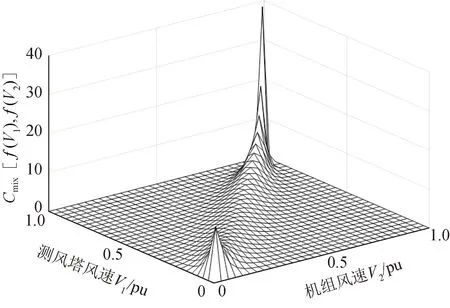
圖8 混合Copula函數概率密度圖 Fig.8 Mixed Copula function fitting graph

為驗證混合Copula函數擬合的優越性,對不同類型Copula函數擬合效果進行比較,如表2所示。

表2 擬合度對比Table 2 Comparison of fit degree

表2中Kendall系數衡量變量間變化趨勢方面的相關性程度,Speaman系數衡量不同變量間的依賴性程度。歐氏距離表示各類Copula函數與經驗分布Copula函數的距離,可以衡量擬合程度的高低[34-35],相關內容詳見附錄E。由表2可知,混合Copula函數的Kendall系數、Speaman函數均與經驗Copula函數相關系數更為接近,同時歐式距離也最小。故本文所提混合Copula函數在擬合風速相關性方面效果優異。

3)風速預測效果對比。

通過將混合Copula函數結合尾流效應可得風電場內各機組風速分布概率,取概率分布期望值為風速預測結果。將本文所提雙驅動風速預測方法與僅采用尾流效應或僅采用Copula函數法獲得的風速預測結果進行對比以驗證預測效果。取風電場內某臺機組全天風速預測結果如圖9所示。

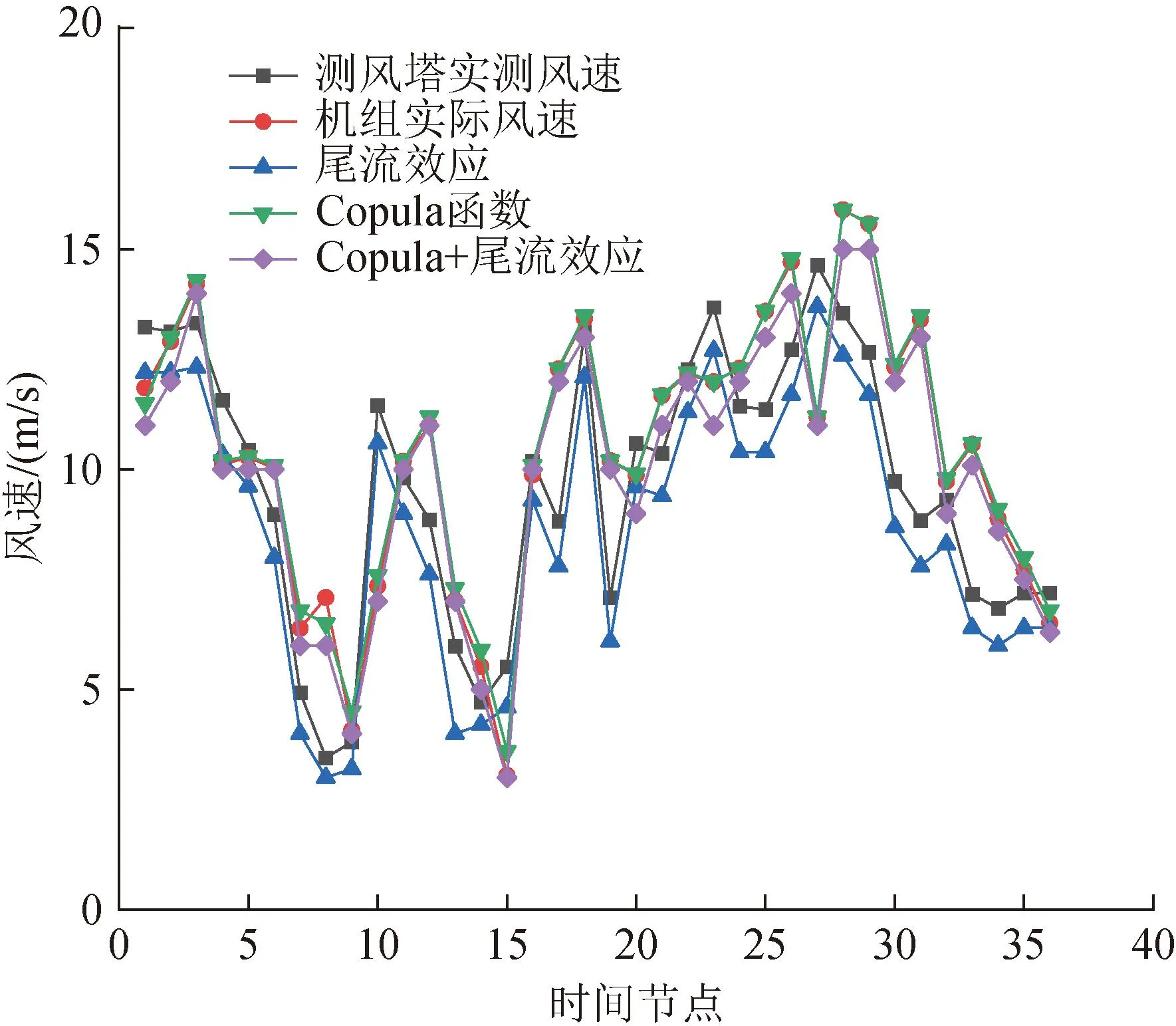
圖9 不同風速預測方法對比 Fig.9 Comparison of different wind speed prediction methods

由圖9可見,僅采用尾流效應的風速預測結果明顯偏離實際值,而僅采用Copula函數的風速預測結果最符合實際風速。為更加直觀比較不同方法的預測準確度,各時間節點預測結果誤差見表3。

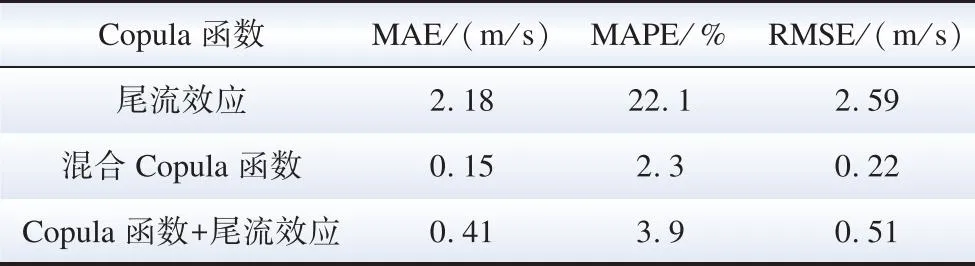
表3 預測誤差對比Table 3 Prediction error comparison

預測誤差分析采用平均絕對誤差(mean absolute error,MAE)表示預測值與實際值之間的相似程度,采用平均絕對百分比誤差(mean absolute percentage error,MAPE)表示對數據的變化敏感程度,均方根誤差(root mean square error,RMSE)可以體現預測值與實際值的整體偏差。由表3可知,Copula函數法預測風速精度最高,其次是本文所提算法,但二者精度差別不大。考慮到風電場內每臺機組并非都適合采用Copula函數分析,且偏遠機組由于相關度較低可能無法發揮Copula函數的優勢,所以僅采用Copula函數的方法不適合實際應用。同時,由Copula函數的構建流程可以看出,僅采用Copula函數預測每臺機組風速會增加計算復雜度。綜上,本文所提風速預測算法在保證較高準確度的前提下,能簡化整體計算流程,提高計算效率。

3.2 單機有效慣量估計

本文參考simulink模塊中雙饋風機模型,并附加虛擬慣量控制、減載控制模塊,對本文所提有效慣量估計算法進行仿真驗證。分析不同風速、不同減載率下雙饋風機慣量響應過程。

仿真輸入風速設置為恒定值8 m/s,在tstart=5 s時設置負荷擾動,機組啟動虛擬慣量響應,不同減載率下的風機輸出電磁功率、捕獲機械功率和轉速變化曲線如圖10所示。

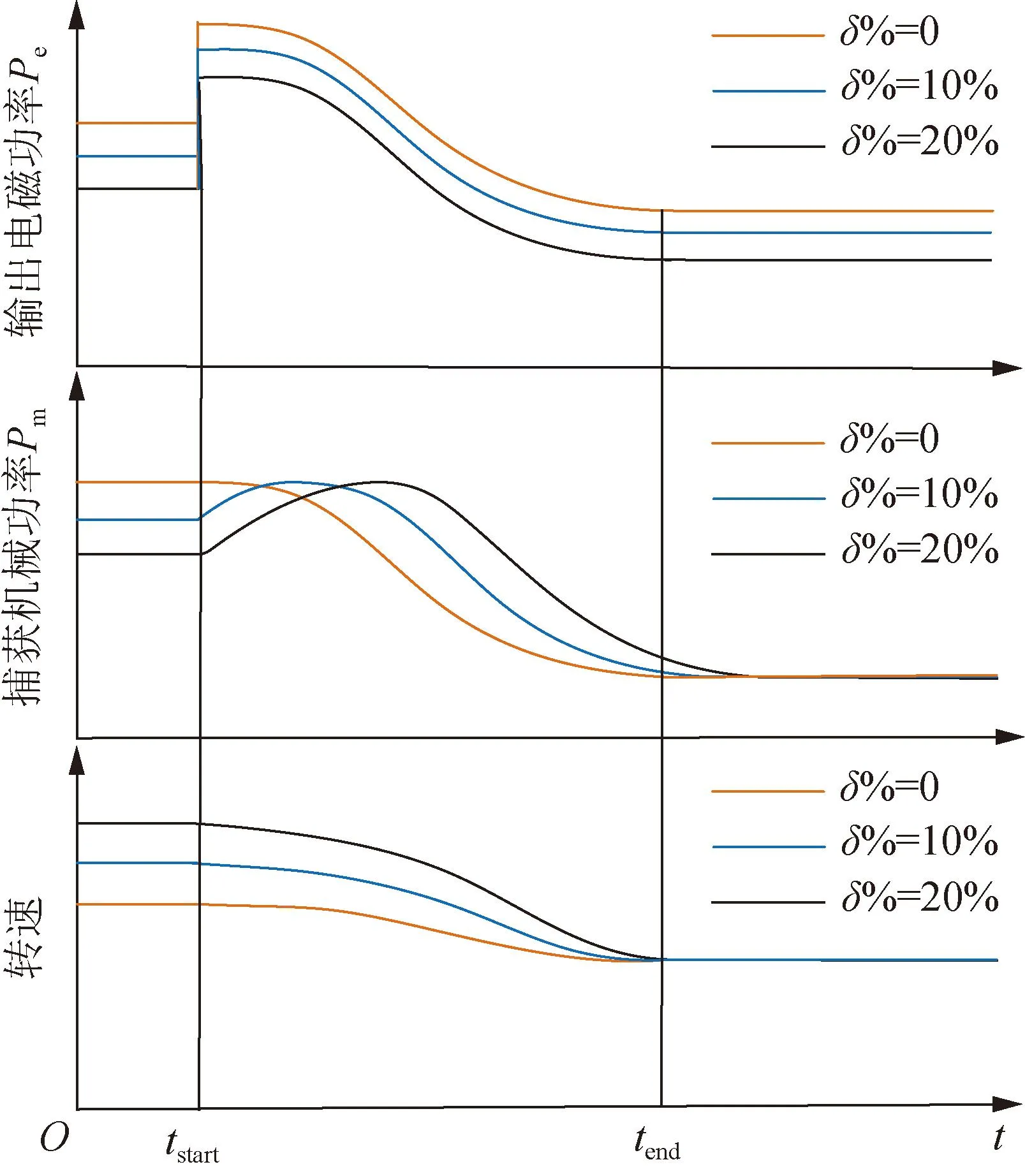
圖10 慣量響應階段變化曲線Fig.10 Phase curve of inertia response

由圖10可知,與非減載運行狀態(δ%=0%)相比,減載運行下,輸出電磁功率和捕獲功率按δ%值大小成比例縮減。慣量響應階段,增發輸出電磁功率隨著轉速的下降逐漸降低。而捕獲機械功率在慣量響應初期呈上升變化,達到最優捕獲功率值后轉為下降狀態,且變化程度由減載率決定。結合公式(14)可知減載運行狀態下,風機捕獲功率損失ΔEM小于正常運行狀態。這也是有效慣量估計過程中不能忽略機組運行狀態差異即減載率差異的原因。

在實際風電場中,風速不斷變化,對此,改變輸入風速值,通過多次重復仿真,得到不同風速下風機慣量響應中各能量值,結果如圖11(a)所示。其中能量轉化損失ΔELOSS無法通過數模仿真測得,只能通過實際機組實驗獲得,為簡化分析過程,取ΔELOSS=5%ΔED。

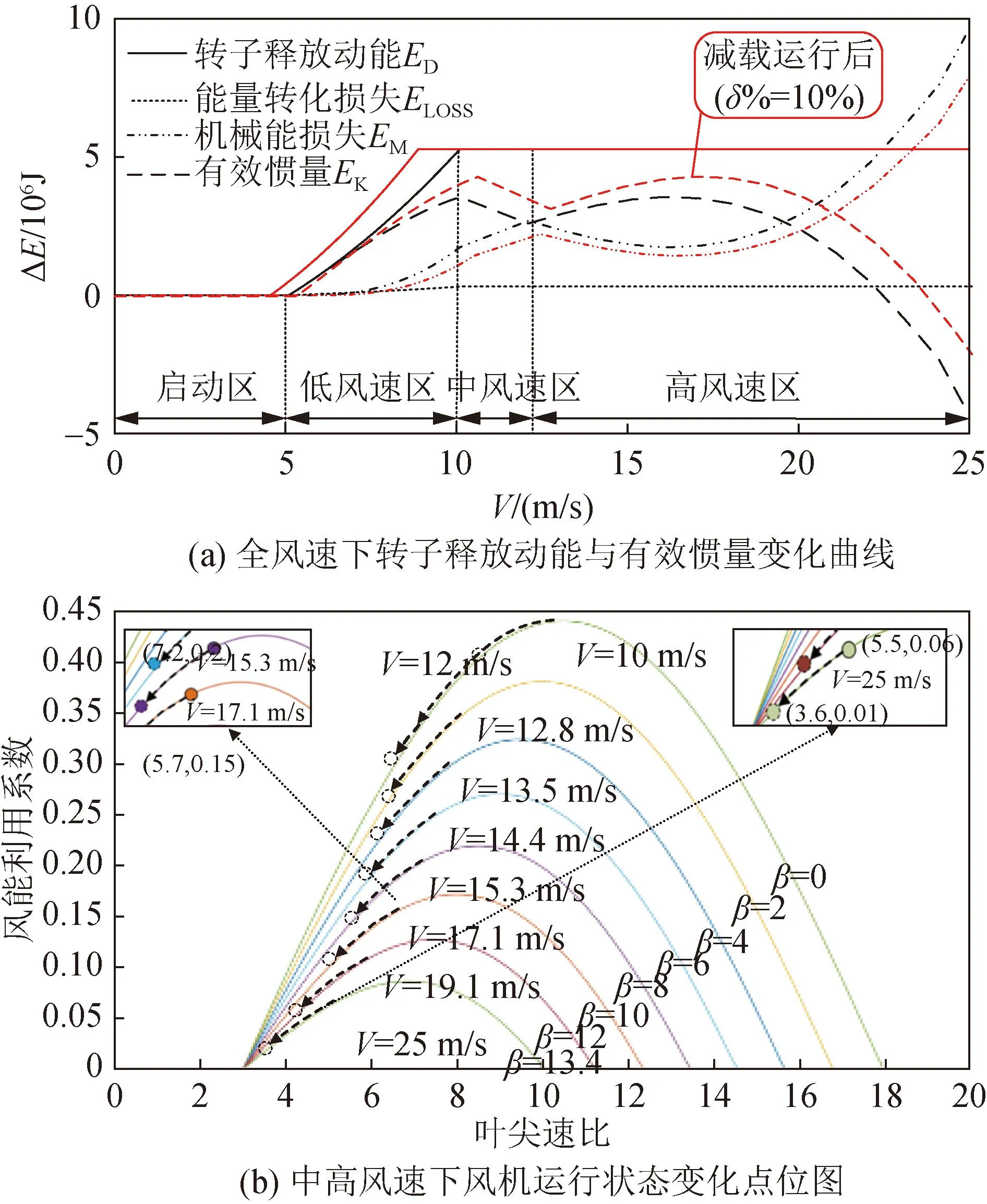
圖11 有效慣量變化曲線及高風速運行點偏移分析Fig.11 Effective inertia change curve and high wind speed operating state migration analysis

由全風速下轉子釋放動能曲線可知,低風速區風機轉子釋放動能與風速呈正相關,當風速達到10 m/s,風機轉子釋放動能不再變化。在恒轉速區機械能損失ΔEM與風速呈正比,在恒功率區ΔEM先減后增。有效慣量隨風速變化特性進行分區定性分析如下:

低風速區(5～10 m/s):MPPT運行狀態下風機有效慣量與風速呈現正相關特性;超速減載狀態下有效慣量曲線沿風速方向平移。

中風速區(10～12 m/s):恒轉速狀態下,風機逐漸達到滿發狀態,轉子轉速保持不變,轉子釋放動能為固定值。而在慣量響應階段,隨著轉速的下降,風機捕獲機械功率大幅下降,導致機械能損失增加,有效慣量降低。

恒功率區(12～16 m/s):通過變槳調節維持功率的恒定。慣量響應時,風機捕獲機械功率隨轉速的下降仍能維持在較高水平,因此機械能損失較低,有效慣量仍然繼續增加。

恒功率區(16～25 m/s):風速極高,槳距角調節程度進一步增加,風能利用系數很低。此時參與慣量響應,隨著轉速的下降風能利用系數到達極低的水平,捕獲功率降低程度較為嚴峻,機械能損失較大致使有效慣量不增反降,甚至低于0。

針對恒功率區下有效慣量先增后降的情況。可通過慣量響應始末時刻風機運行狀態進行定量分析,以間接解釋這種現象。

圖11(b)中不同風速下的運行狀態點對應不同顏色,右側為初始運行點,沿箭頭方向變化到終止運行點。在風速為12 m/s時,隨著轉子動能釋放,風能利用系數由0.42降為0.30,風機捕獲功率降低為初始時刻的71%;風速為16 m/s時,風能利用系數由0.18降為0.15,風機捕獲功率降低為初始時刻的83%;風速為25 m/s時,風能利用系數從0.06降為0.01,風機捕獲功率降低為初始值的16%。由此可推知,風速為12～16 m/s時,始末時刻捕獲功率差值隨風速增大而減小,機械能損失相應減少;風速為16～25 m/s時,風機終止運行點捕獲功率隨風速的增加而急劇減小,最小達到初始功率的16%,損失機械能持續增加,有效慣量下降。由此可解釋有效慣量先增后減的特性。風速為25 m/s時,機械能損失極大,甚至轉子釋放動能不能彌補這部分差值,致使有效慣量為負值,說明高風速下風機調頻能力較低甚至會對實際調頻起負面作用。

3.3 風電場有效慣量估計

以某風電場38臺機組為例,監測數據為各風機機端風速、轉速及功率。采樣間隔為10 min。其中,設置50%機組采用正常追蹤風速變化的方式運行,另外50%采用減載控制(δ%=10%)的方式運行。

利用本文所提雙驅動風速概率預測模型得到38臺機組風速時空分布。并利用本文所提有效慣量與風速關系式,對考慮運行狀態和不考慮運行狀態兩種情景下的風電場有效慣量進行估計。同時依據實際風速測量數據求解風電場有效慣量真實值,結果如圖12所示。

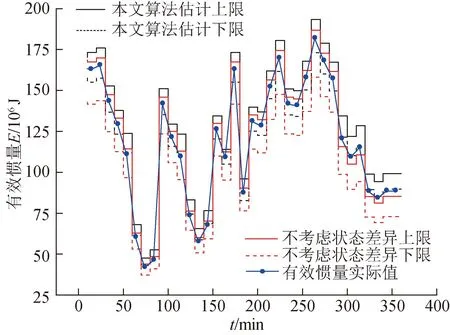
圖12 不同有效慣量算法估計結果對比Fig.12 Comparison of estimation results of different effective inertia algorithms

風速概率預測模型得到的是各機組風速概率分布函數,取90%置信度下的風速預測上下限。進而得到有效慣量估計上下限。由圖12可知,本文所提考慮各機組運行狀態差異的有效慣量估計結果上下限都在有效慣量實際值兩端,而不考慮運行狀態的評估方法,出現多次實際值越限的情況,越限的次數占全部評估次數的18%,特別是在中風速時間節點評估結果越限明顯。表明本文所提估計算法具備明顯的保守性,有效慣量越低時,評估結果越貼合實際值。取置信度為95%時,本文所提算法估計結果越限占比僅為2%,而不考慮運行狀態差異的估計結果越限占比達到31%。表明本文所提算法可有效減小估計值與實際值之間的誤差,準確度較高。

4 結 論

本文提出一種考慮風速時空分布和機組運行狀態差異的風電場有效慣量估計方法。通過軟件仿真和實際算例驗證,得到以下結論:

1) 所提雙驅動風速預測模型能顯著提高風電場風速時空分布預測準確度。尾流效應在分析大規模風電場風速相關性時計算簡便但誤差過大,MAPE達22.1;混合Copula函數擬合準確度優于其他算法,但過程復雜。將兩者結合可以提高風速預測模型的有效性和應用性。

2) 本文提出的單機級別的有效慣量估計方法相比于轉子釋放動能方法更能表征風機實際慣量響應支撐能力。且減載運行狀態下,不僅能預留有功功率,還能改善慣量響應能力,提高慣量支撐水平。

3) 場站級別有效慣量估計方法考慮了各機組機端風速和運行狀態的差異,差異化評估方法貼合風電場慣量水平分布不均的特性。評估結果更符合風電場實際慣量水平,在95%高置信度情境下,評估結果越限率僅為2%,具有良好的準確度。

附錄A

基于非參數核密度估計的邊緣概率分布函數構造方法如下,設{zt|t=1,2,…,T}為樣本空間,相應的概率密度函數為u(z),則利用非參數核密度估計的概率密度函數u(z)為:

(A1)

(A2)

式中:Ww表示函數窗寬;K(γ)表示自變量γ的高斯核密度函數。

附錄B

風能利用系數CP(λ,β)與葉尖速比、槳距角的關系展開式見式(B1),繪制的三維關聯如圖B1所示。具有以下特性:當槳距角固定不變時,存在唯一的風能利用系數最大值;對于任意λ,隨著β的增大,CP明顯減小。

(B1)

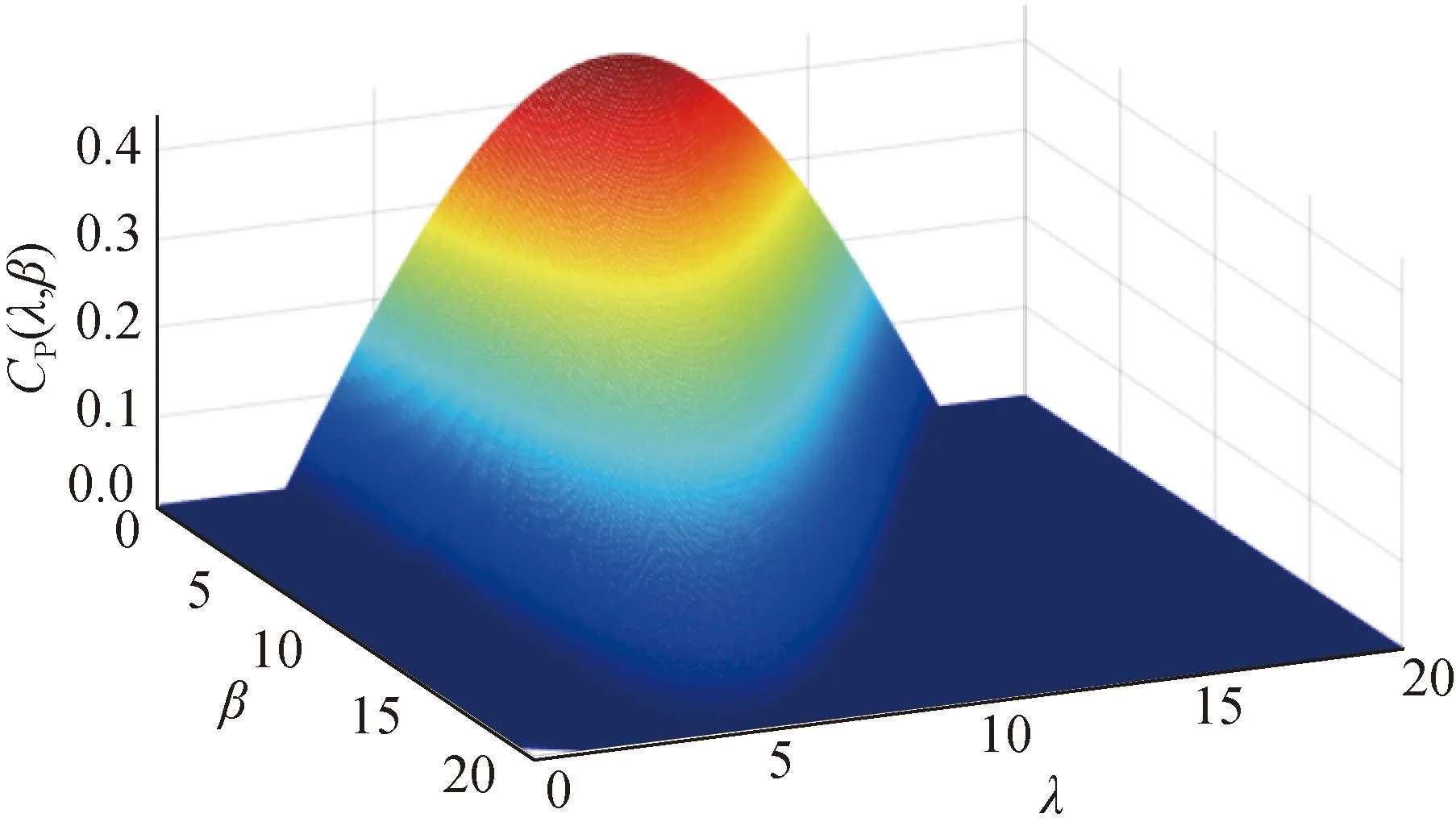
圖B1 風機風能利用系數三維曲面圖Fig.B1 Three-dimensional surface diagram of wind energy utilization coefficient of fan

附錄C

有效慣量展開解析式如式(C1)所示:

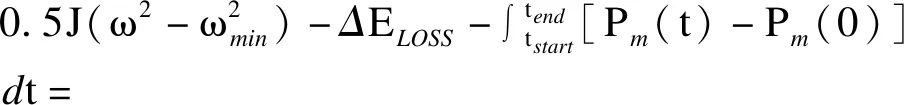
(C1)

式中能量轉化損失ΔELOSS需要通過實驗測得,而每次實驗轉子動能大小不同,轉子動能轉化為有效慣量的過程中的能量損失也不同,為避免每次計算都要進行實驗,通過經驗總結發現轉化能量損失與轉化能量大小有關,近似為線性比例關系,由此可通過多次實驗獲取平均比例系數k。則能量轉化損失可轉化為轉子釋放動能的k倍。

變槳調節控制下風能利用系數修正為下式:

(C2)

附錄D

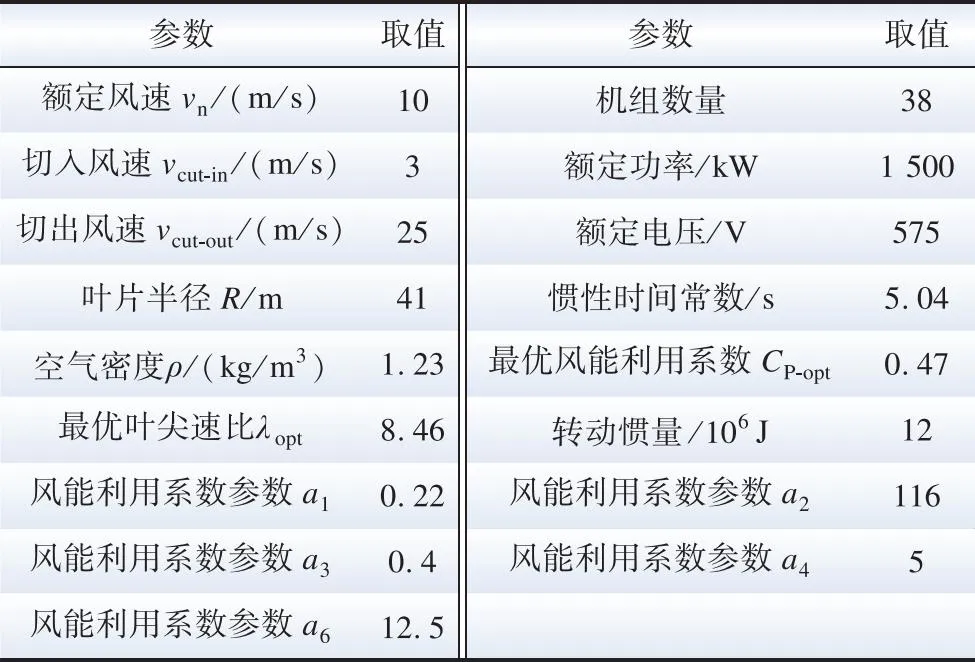
表D1 仿真算例參數Table D1 The parameters are verified by simulation and examples

附錄E

經驗Copula函數及歐式距離定義:

定義1(經驗Copula函數):經驗Copula函數由原始數據觀察得到。設隨機變量X和Y由S組數據構成,且其經驗分布函數分別為FS(x)和HS(y),則經驗Copula函數的定義式如式(E1)。

(E1)

式中:u,v∈[0,1];中間量H為判定函數,當FS(xi)≤u成立時,I[FS(xi)≤u]=1,否則I[FS(xi)≤u]=0。I[HS(yi)≤v]的判定原理同上。

定義2(歐氏距離):各類Copula函數Cp(ui,vi)與經驗Copula函數間的歐式距離dC表達式如式(E2)。

(E2)

式中:p表示Copula函數的類型。不同類型Copula函數中,dC值越小說明擬合原始數據的效果越好。