考慮風電時空特性和相對波動率的平衡成本分攤方法

何義瓊,李鑫,賈海清,劉長璽,劉茹,谷旭東,雷霞

(1.內蒙古東部電力交易中心有限公司,呼和浩特市 010000;2.西華大學電氣與電子信息學院,成都市 610039)

0 引 言

“十三五”以來,全國風電發展迅速,棄風限電情況逐年改善明顯。2021年全國風電新增并網裝機容量4 757 kW,同比增長16.6%;風電年發電量6 526億kW·h,占全部電源總發電量的7.8%;年棄風電量208.8億kW·h,棄風率下降至3.1%。“十四五”是電力低碳轉型的關鍵期,大力發展風電依舊是主旋律,現階段更為積極的目標應是在提升風電消納能力的基礎上,進一步完善電力交易機制和價格激勵方式,促進風電和電網的可持續發展[1-2]。目前,我國現貨市場建設如火如荼,其通過短時間尺度的快速交易及與中長期市場的配合,可進一步緩解風電波動對電網運行的影響并減少棄風,這也對挖掘短時間尺度的風電成本提出了更高要求。此外,風電仍以平準化度電成本為基準報價,其并網產生的成本在市場交易中未量化體現,這不利于系統對風電的接納。只有全面厘清與現貨交易時間尺度一致的風電分時段真實成本,才能保證新能源現貨市場交易的公平性,并促進系統精準調度方案的制定。

風電作為清潔能源對于節能減排具有正向價值,但風力發電易受環境和自然資源影響,具有波動性和不確定性,因此,風電并網后需要常規機組或儲能的啟停、調節、預留備用等一系列操作來確保電力系統的實時有功平衡[3],由此帶來的系統額外運行成本即為“平衡成本”[4]。針對風電平衡成本計算方法與定性分析的問題,國內外學者進行了大量的研究工作。文獻[5]對大規模風電并網的美國德州電力市場進行了研究,指出在該市場環境下,風電并網會對市場其他參與者產生影響,評估風電價值不能忽視風電與其他電源之間的影響關系;文獻[6]研究了英國風力發電對系統平衡成本的影響,結果表明風電并網容量增大時,系統平衡成本顯著增加;文獻[7]研究了風電并網時平衡成本的量化方法,基于線性回歸和隨機規劃的方法對不同風電滲透率下的平衡成本進行了計算;文獻[8]結合電力系統優化調度分析了風電波動對電網運行的影響,提出應構造無風電平衡成本的等效場景,使風電能源價值從平衡成本中剝離,在等效時將風電出力處理為恒值出力;文獻[9]研究了定量分析風電平衡成本的計算思路,并分季節對不同風電接納量系統的平衡成本進行了測算分析;文獻[10]基于波形相似理論度量風電場實際出力曲線和等效出力曲線的波動整體性差異,兼顧風電場裝機容量的影響,確定各風電場因未能有效跟蹤負荷波動而承擔的風電波動成本份額;文獻[11]研究了基于平衡成本的調峰補償成本測算方法,并在其基礎上提出了風電分段調峰補償機制,結果表明棄風段的風電因平衡成本過高而交易價值較低。以上研究工作主要針對風電在較長時間段或調度周期內總的平衡成本進行定量和定性分析,難以滿足現貨市場短時間尺度交易的需要,因此,有必要對風電功率短時間尺度的波動特性及其量化評估方法進行研究。

目前已有很多針對風電波動特性方面的研究。文獻[12]提出一種考慮最優核函數帶寬選擇的改進型非參數核密度估計法,建立了風力發電隨機分布模型,從不同時間尺度分析了不同區域間的風電出力概率特性差異;文獻[13]提出了一種基于混合尺度參數和位置參數的t分布模型對風電功率波動變化率進行擬合,該方法基于統計原理,在對風電功率波動的研究過程中消除了時序特征;文獻[14]研究了在不同裝機容量和不同差分尺度下的風電功率波動特性,結果表明風電功率波動在時間尺度分布上具有趨勢性;文獻[15]研究了風電功率波動在不同時間、空間尺度上的分布特性,研究結果表明,隨著風電場群空間分布廣度的增大會使得風電功率的波動出現平緩效應,但并未對波動進行定量的刻畫;文獻[16]研究了不同時間分辨率下各時段風電功率波動的統計特性,實現了具有時序特征的風電功率波動特性的定量分析;文獻[17]提出了分析風電功率時間序列波動性與預測誤差關系的方法,對風電功率波動的時序特征進行了較為準確地描述。上述關于風電功率波動性的研究,對其功率時間序列的演進變換特征進行定量刻畫的方法主要運用統計學模型,對數據要求過高,從而降低了在風電波動成本分攤中應用的實用性。

針對上述問題,本文從對風電功率波動特性的分析出發,提出一種考慮風電時空特性和相對波動率的平衡成本分攤方法。首先,構造“等電量-順負荷”場景,考慮風電每日的出力特性,對一天的系統運行進行優化調度,對比預測場景和等效場景優化調度的系統總運行成本計算得到調度周期內總的風電平衡成本[9-10];其次,兼顧風電場的空間分布和容量對平衡成本分攤的影響,提出風電平衡成本的空間分布分攤方法。隨后,提出一種用于刻畫風電功率波動時序特性的指標即分時段三角系數,在此基礎上進一步定義用于量化風電功率分時段波動的分時段波動率,以及反映風電相對負荷波動程度的指標即分時段相對波動率;最后,以各時段相對波動率指標為依據對風電平衡成本進行逐時段的分攤,即得到風電分時波動成本。最后以某地區含高比例風電接入的網架結構進行數值仿真分析,驗證所提方法的有效性。

1 風電相對波動性及平衡成本分析

波動性是一種描述物質運動規律的物理學概念,強調的是物質的時變特性,只要事物處于持續變化的狀態,就一定存在波動。據此,風電的波動性則指風電的輸出功率隨時間的持續變化狀態。風電波動性產生的根本原因在于風機的動力元素——風能受天氣和地勢等多種不可抗拒的自然因素影響,且目前風電機組控制功率波動的能力有限,因此波動性是風電的固有特性。即使風電預測具有很高的準確度,甚至不存在預測誤差,風電出力仍然會表現出波動性。

風電作為電源,難以像水電、火電等常規機組那樣“完美”地跟蹤負荷,而且其呈現的波動性及反調峰特性使得風電出力與負荷的變化趨勢難以同步[18-20],因此從調度資源來看,風電既具有電源特性也具有負荷特性[21]。本文將風電與負荷的持續相對運動形式定義為風電相對波動性,將其認為是風電出力中的電源異質性,呈現的是風電的負荷同質性,是平衡成本產生的根源。

隨著風電并網規模的逐步增大,風電相對波動性會對系統的運行特性造成影響[22-23]。一方面,系統凈負荷的峰谷差及變化率會因風電相對負荷的波動而改變,此時,常規機組調節自身出力不僅需要實現負荷的實時匹配,還要平抑因風電并網可能導致的更大凈負荷峰谷差及變化率,這勢必會使得其啟停等調節成本大大增加;另一方面,風電并網使系統轉動慣量減少,降低了電網的耐頻能力,需要預留一定的旋轉備用以確保系統的安全穩定運行,使得系統預留備用容量的費用也進一步增加。因此,為了保證系統的供需平衡和安全穩定,系統需對各機組啟停、出力和旋轉備用等進行調節,這部分額外的系統響應成本即為風電的平衡成本。

2 風電分時段平衡成本計算

風電平衡成本的產生源于風電的相對波動性,需要由系統調度常規機組來進行平抑,因此其量化可利用電力系統運行的優化調度模型完成。求解風電分時段平衡成本的關鍵在于:1)將常規機組平衡風電波動的調度成本與平衡負荷波動的調度成本剝離;2)根據各風電場的容量大小及其波動特性對系統平衡成本的影響程度,將剝離出的調度成本分攤至各風電場;3)精準刻畫在各調度時段風電出力相對負荷波動功率的時序演進特征,探尋風電平衡成本合理分攤至各時段的依據和方法。由于構成風電平衡成本的主體是常規火電機組,為平抑風電相對負荷波動而實施啟停、調用出力及提供旋轉備用而產生的成本,且各調度時段平衡成本的產生并不孤立,而是存在著必然的耦合因素,因此,計算分時段平衡成本不能簡單地僅基于各時段系統局部優化調度結果進行求解,而應該先求解系統調度周期內總的平衡成本,再遵循合理原則對平衡成本進行時段分攤。

風電分時段平衡成本的計算框架如圖1所示。

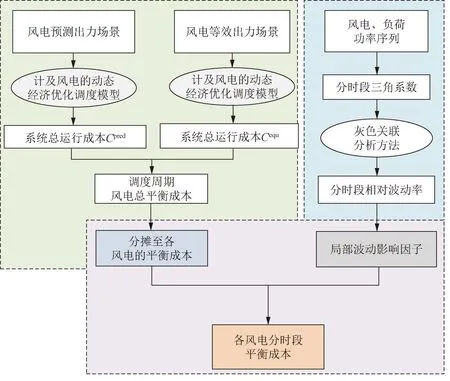
圖1 風電分時段平衡成本計算框架Fig.1 The proposed calculation method flowchart of time-segment balance cost of wind power

首先對風電預測出力場景進行等效,得到零風電平衡成本的風電等效出力場景,分別計算2種場景下的系統總運行成本,二者之差即為調度周期風電總平衡成本;通過分時段三角系數對風電相對負荷波動功率序列的時序演進特征進行定量提取,基于灰色關聯分析方法在一定時間窗口內(本文取15 min)篩選分時段三角系數的次優解,歸一化處理后得到逐時段描述風電相對負荷局部波動程度典型狀態的分時段相對波動率;以各時段風電相對負荷波動功率的局部典型狀態對整個調度周期風電相對負荷功率的宏觀波動特征的影響(即局部波動影響因子)大小為依據,對調度周期內風電總平衡成本逐時段分攤,即得到15 min時間尺度的風電分時段平衡成本。

2.1 調度周期風電總平衡成本計算方法

針對上述思路的關鍵點1,本文利用文獻[9-10]提出的“等電量-順負荷”方法構造了一個零風電平衡成本場景,將風電等效為調度周期內輸出功率能夠始終跟蹤負荷的等效替代電源。基于系統優化調度,通過計算風電預測出力場景和風電等效出力場景下系統總運行成本差異,得到風電調度周期內的總平衡成本。

圖2 風電等效替代電源構造示意Fig.2 Equivalent alternative power supply construction diagram of wind power

風電等效替代電源構造方法為:

(1)

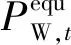
2.2 計及風電的動態經濟優化調度模型

本文構建的計及風電的動態經濟優化調度模型的目標是在滿足負荷及系統安全運行約束的前提下同時優化火電機組出力、火電機組啟停及旋轉備用優化配置,使調度周期內的系統總運行成本最小。

目標函數為:

minCTOC=min(CG+CSU+CSR+CW)

(2)

式中:CTOC為系統的總運行成本;CG、CSU、CSR分別為火電機組的發電成本、啟停成本、預留旋轉備用成本;CW為風電運維成本。

1)火電機組發電成本。

(3)

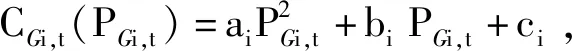
2)火電機組啟停成本。

(4)

(5)

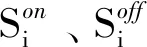
3)風電的運維成本。

(6)

式中:kW為風電場的單位運維成本;PWj,t為風電場j在t時刻的計劃出力;NW為風電場數。

4)火電機組預留旋轉備用的成本。

(7)

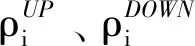
約束條件包含以下部分:

1)系統有功功率平衡約束。

(8)

式中:PL,t為t時刻總的負荷預測功率。

2)機組出力約束。

(9)

(10)

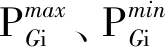
3)火電機組爬坡約束。

(11)

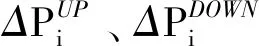
4)最小啟停時間約束。

(12)

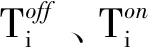
5)旋轉備用約束。

(13)

(14)

6)線路有功潮流約束。

本文中潮流約束考慮直流潮流模型,各支路有功潮流通過發電機輸出功率轉移分布因子矩陣Gln計算得到。

(15)

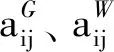
為第l條線路的有功傳輸上限。

將火電機組發電成本分段線性化處理后,利用上述混合整數線性規劃模型分別得到調度周期內風電預測出力場景下的系統總平衡成本Cpred和風電等效出力場景下的系統總平衡成本Cequ,再由式(16)計算可得一個調度周期內風電總的平衡成本Ctot。

Ctot=Cpred-Cequ

(16)

2.3 風電平衡成本的空間分布分攤方法

實際系統中往往存在多個風電場并網,如果單獨計算各自產生的平衡成本,則忽略了風電場之間的集群效應。本文綜合考慮各風電場容量和對系統運行的影響大小,將總平衡成本分攤至各風電場,以解決關鍵點2。

風電平衡成本的空間分攤方法如下所示:

1)計算各風電場的單一平衡成本。在計算第j個風電場的單一平衡成本時,將其余風電場預測出力按前文所述等效處理,保留第j個風電場的原預測出力。計算第j個風電場原預測出力下的調度成本與風電場全部等效出力的調度成本差值,以該差值作為風電場j的單一平衡成本Cj。

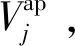
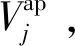
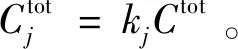
2.4 分時段相對波動率

針對關鍵點3,本文提出基于分時段三角系數的定量提取風電相對負荷波動功率時序演進特征的指標——分時段相對波動率。分時段三角系數與傳統評估風電波動的一階差分形式指標[24-25]側重點各有不同。后者模型簡單易懂且已經在衡量各種能量波動的研究中得到廣泛的應用,其重點在于描述相鄰時刻波動功率的變化;前者為了與逐時段合理分攤風電平衡成本的目標相契合,更著重于捕捉風電相對負荷波動功率序列在各時段內的持續波動特征。為了與現貨交易時間尺度保持一致性,本文將風電相對波動率的時段定為15 min。

圖3為風電相對負荷波動功率序列的15 min三角系數求解示意圖,圖中標注了個別功率極值點、非極值點、功率三角形的幅值U及相角θ。通過不同功率三角形的幅值U和相角θ可對該時段風電相對負荷功率的持續波動狀態進行定量描述。

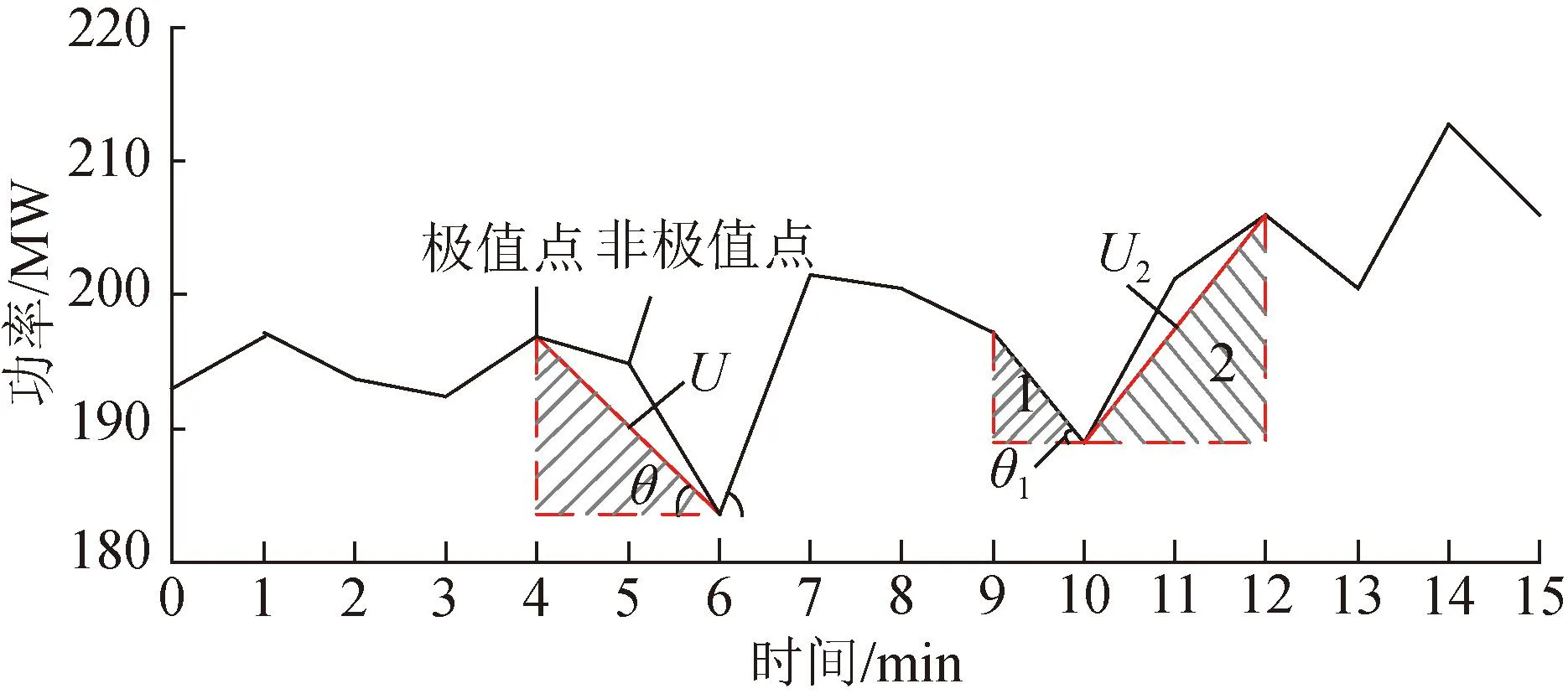
圖3 功率序列分時三角系數示意圖Fig.3 Diagram of time-sharing triangle coefficient of power sequence

1)逐小時輸入1 min時間尺度風電相對負荷波動功率序列PW-L(1),PW-L(2),…,PW-L(k),…,PW-L(15)。

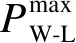
(17)

(18)

3)忽略功率序列中的非極值點,形成新的功率序列P′W-L,序列中相鄰2個數據點間連線與垂直和水平方向相交后形成功率三角形,如圖3中陰影部分所示。

4)計算功率序列P′W-L中各功率三角形的幅值和相角,二者共同構成分時三角系數。

在每15 min內的風電相對負荷功率序列中,如果某時段的風電相對負荷波動劇烈,則該段時間的波動功率序列變化過程應呈現變化時間快、波動幅度大的特征,即該時段的三角系數應同時滿足幅值最大和相角最大2個條件。但上述2個條件難以同時滿足,如圖3所示,功率三角形1具有最大相角θ1,而功率三角形2具有最大幅值U2,在該時間段內,最大相角和最大幅值并未同時出現,故采用灰色關聯分析法這一多屬性決策方法以尋求此15 min內幅值和相角的次優解。

灰色關聯決策提供了一種衡量不同因素間關聯程度大小的重要量化處理方法,該方法能夠找出理想最優方案對應的效果評價向量,由決策問題中各個方案的效果評價向量與最優方案效果評價向量之間的灰色關聯度大小確定問題的最優解決方案和優劣排序[26-28]。通過灰色關聯分析方法可挖掘代表風電相對負荷波動功率序列各時段波動程度典型狀態的分時段三角系數,具體步驟如下:

1)根據事件集A={a1,a2,···,an}和對策集B={b1,b2,···,bm}構造局勢集S={sij=(ai,bj)|ai∈A,bj∈B}。本文中以各時段風電相對負荷的持續波動狀態為事件集A={a1,a2,···,a12},分時段三角系數的幅值和相角作為對策集B={U,θ}。

2)確定決策目標k,k=1,2,···,s。

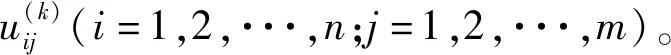
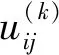
(19)

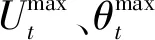
(20)

依據式(20)提取的各調度時段風電相對負荷局部波動程度特征量(即分時段相對波動率),對完整調度周期內風電相對負荷宏觀波動狀態的影響(即局部波動影響因子)大小,將調度周期內各風電場分攤的平衡成本逐時段進行分攤,即得到風電分時段平衡成本。

(21)

(22)

式中:Cj,t為風電場j在t時刻的風電分時段平衡成本;φj,t為風電場j在t時刻相對波動率的局部波動影響因子。

3 算例分析

3.1 算例參數概述

本文采用某地區32節點含高比例風電接入的網架結構作為計算調度周期內風電分時平衡成本進行仿真分析,系統拓撲結構如圖4所示,調度時間尺度設置為15 min。

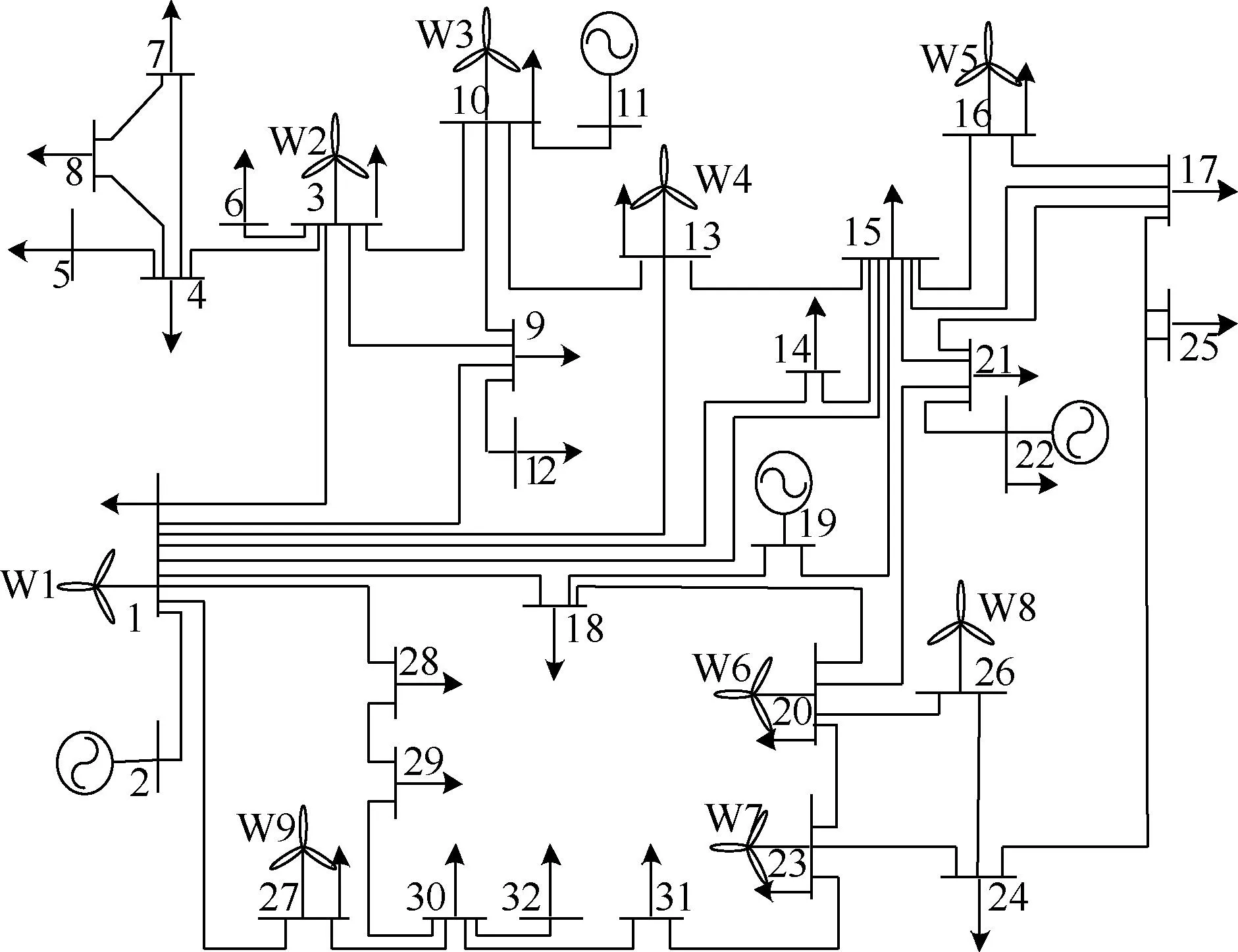
圖4 某地區32節點網架結構Fig.4 32-node grid structure in a certain area

該系統包含4臺火電機組,參數見表1,9個風電場,風電出力和負荷功率數據采用該地區的歷史數據。其中火電裝機容量為2 000 MW,占比28.6%;風電裝機容量為5 000 MW,新能源發電占比71.4%。火電機組旋轉備用成本為120元/(MW·h),棄風懲罰成本為160元/(MW·h)。求解各風電場出力相對于負荷的分時段波動率時,選取時間尺度為1 min的風電、負荷預測功率序列。

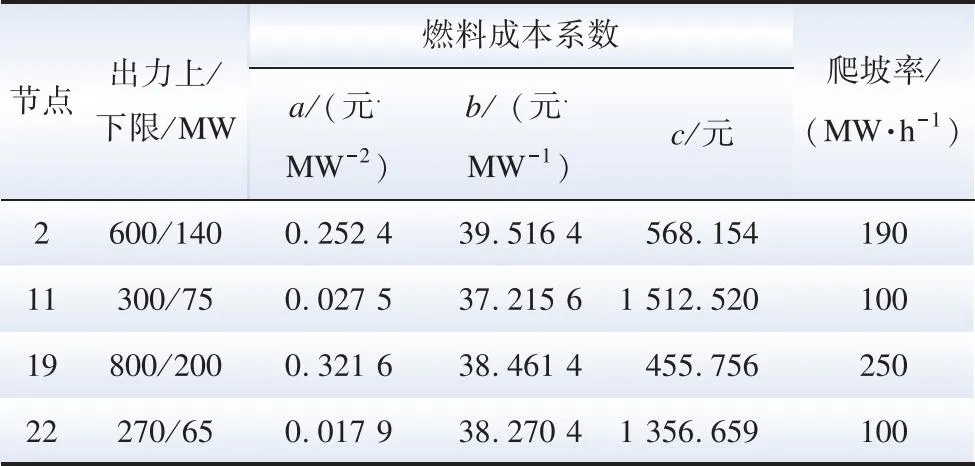
表1 火電機組運行參數Table 1 Operation parameters of thermal power units

3.2 算例結果及分析

3.2.1 風電場平衡成本分攤結果

根據本文所提風電場平衡成本分攤方法,計算出某典型日的總平衡成本為10 822.4元,其中9個風電場的分攤成本如表2所示。

表2 風電平衡成本分攤Table 2 Balance cost allocation of wind power

表2反映了9個風電場的分攤系數及各自的分攤成本。由表2可知,W1的單位平衡成本為中等水平,但由于其容量遠大于其他風電,對系統產生的影響最大,因此分攤到的平衡成本最多;W3并網下單位容量引起的平衡成本最小,且其容量也較小,因此分攤系數最小,分攤到的平衡成本最少;W8雖然容量最小,但由于其波動特性對系統安全運行影響較大,所以其分攤的平衡成本比較大。

3.2.2 風電的空間分布對平衡成本分攤的影響分析

為分析風電的空間分布對平衡成本分攤的影響,本文將W7、W8的容量相易,同時不改變其出力預測曲線的波動趨勢,再根據本文所提風電場平衡成本分攤方法重新進行計算,計算得到某典型日的總平衡成本為11 351.70元。各風電場的分攤成本如表3所示。

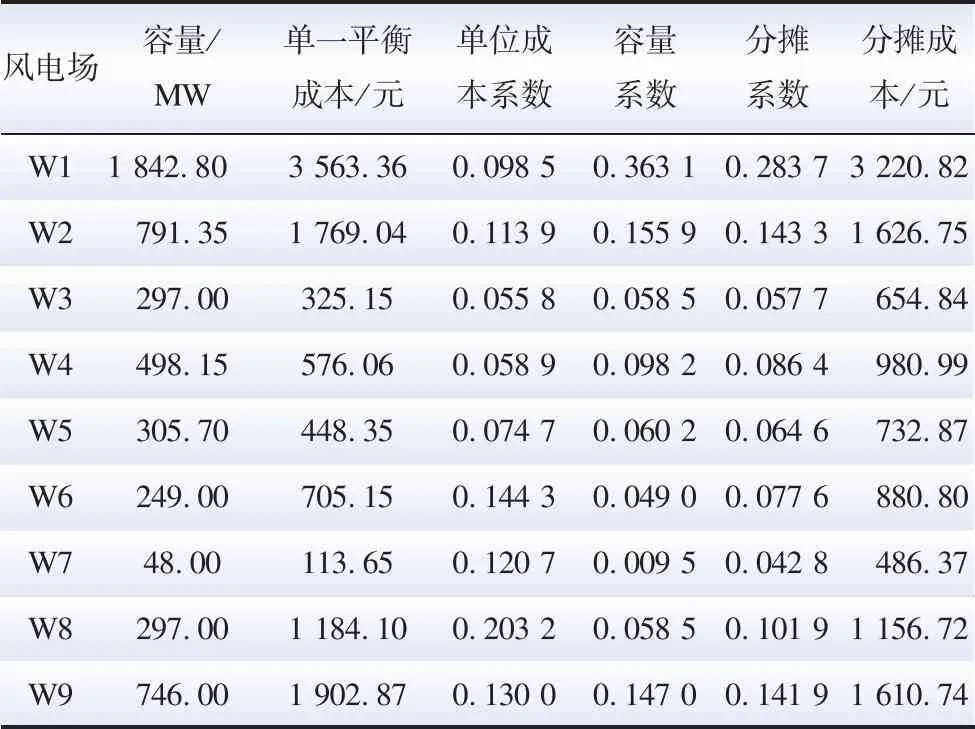
表3 W6、W7容量相易后風電平衡成本分攤Table 3 Balance cost allocation of wind power after capacity conversion of W6 and W7

在W7和W8容量相易,出力預測曲線波動趨勢不變的情況下,系統的總平衡成本是略微有所增加的,對比表2和表3中W7和W8的單位成本系數可知,系統總平衡成本的增加是由于相對負荷波動程度更大的W8的容量增大引起的。對比表2和表3中W7和W8的分攤成本可知,在機組容量變化、出力預測曲線波動趨勢不變的情況下,各機組的并網容量發生改變會影響其分攤到的平衡成本。對比表3中容量相同的W3和W8機組可知,在容量相同的情況下,風電場的單位成本系數更高,則其分攤到的平衡成本更大。這說明風電場相對負荷波動程度的大小會影響到平衡成本的分攤。

由以上結果分析,風電場在系統中所處的空間位置將會影響其并網產生的平衡成本,這是由于風電場所處的地理位置不同,其風力資源也不同,進而導致其風電的出力特性不同。同時,在同一地理位置,若風電場的容量增大,則其對系統的影響也將增大。本文所提風電平衡成本的空間分布分攤方法在進行系統總平衡成本分攤時,同時考慮了風電場容量及其相對負荷波動程度對系統總平衡成本分攤的影響。

3.2.3 風電波動程度對分時段平衡成本的影響分析

為分析風電出力波動程度對分時段平衡成本的影響,本文選取表2中容量相近且分攤成本基本相同的風電場W6、W7進行分析。圖5為W6、W7的凈負荷曲線以及其分時段平衡成本。通過對比分析不同風電波動程度下風電分時段平衡成本的差異和變化來確定其影響關系。

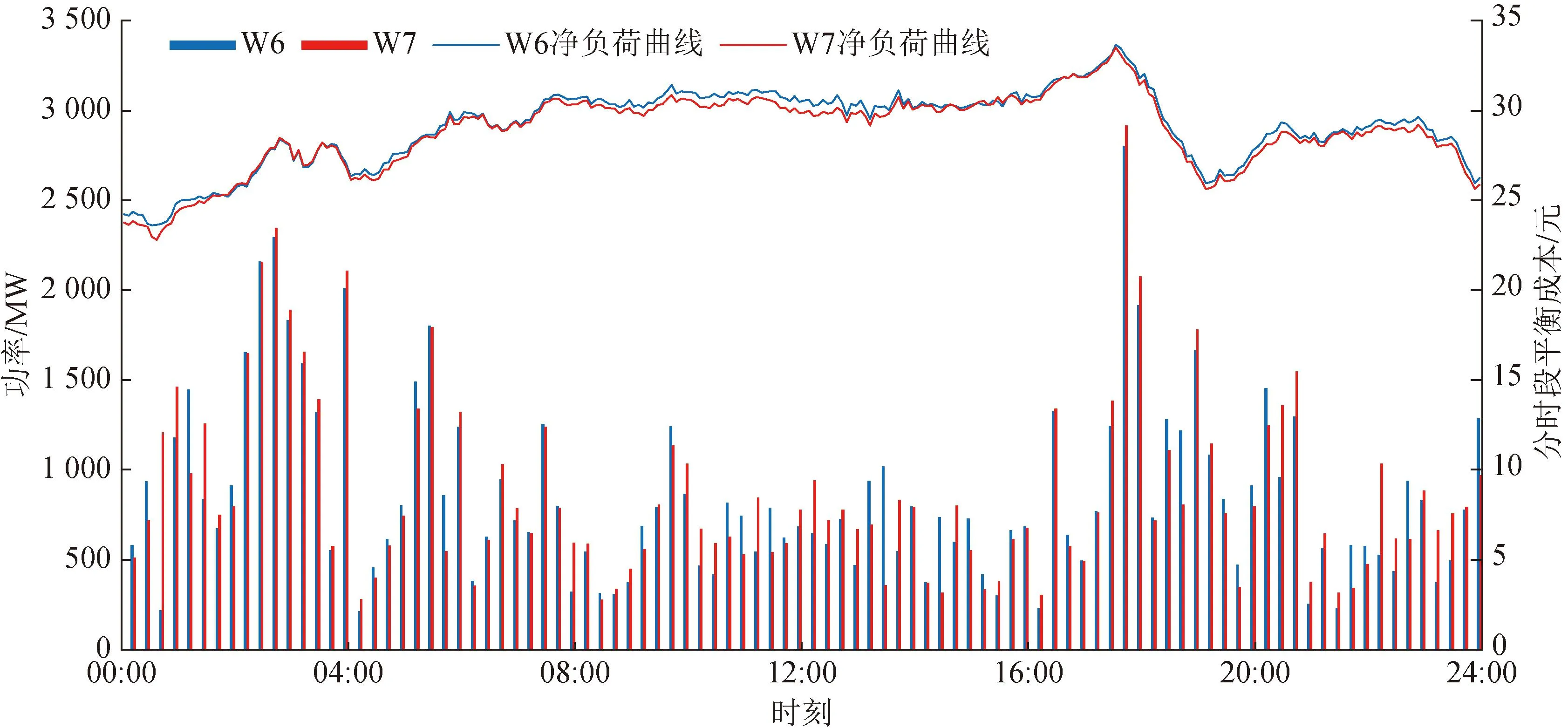
圖5 W6、W7凈負荷曲線及分時段平衡成本對比Fig.5 Comparison of net load curves and time-segment balance costs of W6 and W7

結合圖5可知,各時段的平衡成本大小與風電場的凈負荷曲線的波動程度呈正相關,風電場凈負荷曲線的波動程度體現了風電場追蹤負荷的能力。在凈負荷曲線波動較劇烈的時候,表明風電追蹤負荷的能力較差,該時段的平衡成本就較高,如圖5中17:00—20:00所示。反之,凈負荷曲線波動較平穩的時候,表明風電追蹤負荷的能力較好,該時段的平衡成本較低,如圖5中08:00—16:00所示。在圖5中,W6、W7的凈負荷曲線整體趨勢大體相近,但各個時段內的波動率存在差別,這也導致了兩者在各個時段內的分時段平衡成本有所差異。本文所提的分時段相對波動率為風電總平衡成本進行逐時段分攤提供了量化依據。

4 結 論

為解決新能源現貨市場的定價問題,針對風電接入電網后其固有的波動性給常規機組帶來的額外調節成本,本文結合日前優化調度模型,研究了一種基于風電相對負荷波動功率特性分析的風電分時段平衡成本計算方法。提出了定量描述風電相對負荷波動功率序列時序演進特征的指標即相對波動率,并基于相對波動率獲取局部波動影響因子對風電調度周期總平衡成本進行了逐時段分攤,通過算例仿真驗證了模型的有效性,得到不同風電并網容量、不同風電波動程度下的分時段平衡成本計算結果。從算例結果可以看出,風電并網容量越大,其對系統平衡成本產生的影響也就越大;風電在某時段內相對于負荷波動越劇烈,則在該時段對應的平衡成本也越高。且風電的平衡成本是一個動態值,會隨著風電功率、負荷需求的實時波動及系統靈活調節能力的改變而持續變化。本文所提的風電分時段平衡成本計算方法,一是對風電場在某地理位置的容量規劃有一定的指導意義;二是對后續建立健全現貨市場風電交易機制和價格激勵方式具有一定的實際價值,亦可為風電消納的輔助服務市場價值研究提供理論分析基礎。