NPC/H橋逆變器調制策略及其中點電位控制

朱玉振

（國網山東省電力公司菏澤供電公司，山東 菏澤 274000）

0 引言

多電平逆變器拓撲結構主要有中點鉗位（neutral point clamped，NPC）型、飛跨電容型和H 橋級聯型［1-2］。H 橋級聯型又包括2H 橋和3H 橋，3H 橋即中點鉗位型H（neutral point clamped H，NPC/H）橋［3］。NPC/H 橋級聯型多電平逆變器兼具NPC 型多電平逆變器和2H 橋級聯型多電平逆變器的優點，相比NPC 型多電平拓撲，鉗位二極管的數量減少，電容中點電位控制方法簡單；相比2H 橋級聯型多電平拓撲，無需過多的獨立直流電源［4-5］。

多電平逆變器調制策略中，相比載波脈寬調制策略，空間矢量脈寬調制（space vector pulse width modulation，SVPWM）策略具有直流側利用率高、輸出畸變低、算法靈活等顯著優點［6］。SVPWM 策略同樣存在需要解決的問題：隨電平數增加，其算法的計算量呈指數增加，程序代碼冗長，精度和實時性降低；傳統SVPWM 算法采用七段式開關序列，在低開關頻率工況下，冗余的電平跳變使輸出畸變更大。因此，針對多電平逆變器SVPWM 算法復雜性的簡化以及輸出性能的優化，具有較大的現實意義［7-8］。

NPC 型逆變器的電平數越多，直流側電容電壓波動問題越復雜［9-11］。與NPC 型逆變器相比，文中研究的NPC/H 橋型逆變器每相由一個NPC/H 橋功率單元構成，電容電壓平衡方法較易實現。一是從硬件上實現平衡，每個均壓電容采用獨立直流源，但增加裝置成本［12］；二是在調制環節中增加控制算法達到平衡電容電壓目的［13-14］。如文獻［15］提出一種新型三相嵌套式中點鉗位型四電平逆變器，根據電容電壓偏差和電流方向合理選擇中間兩個電平對應的冗余開關狀態，從而控制懸浮電容電壓。

文中以NPC/H 橋五電平逆變器為研究對象，分析其主電路工作原理、電容電壓不平衡原因，研究其SVPWM 策略以及中點電位平衡方法。

1 NPC/H橋逆變器主電路分析

圖1 為NPC/H 橋五電平逆變器拓撲結構，三相電路均為二極管鉗位型三電平全橋結構；帶三相負載；每相均有一個獨立直流源，由兩個均壓電容分壓。開關器件VxR1、VxR2、VxR3、VxR4串聯構成右橋臂，右上、右下橋臂中點分別通過鉗位二極管DxR1、DxR2與電容中點連接；開關器件VxL1、VxL2、VxL3、VxL4串聯構成左橋臂，左上、左下橋臂中點分別通過鉗位二極管DxL1、DxL2與電容中點連接，直流側電壓為Udc，均壓電容為Cx1、Cx2，其中x∈｛A，B，C｝，o為三相逆變器的中性點。為避免橋臂直通，每個半橋的開關管驅動脈沖互補，如VxR1與VxR3互補，VxR2與VxR4互補。理想狀態下均壓電容電壓為Udc/2，每相輸出五種電平Udc、Udc/2、0、-Udc/2、-Udc，對應9 種開關狀態［16-17］。

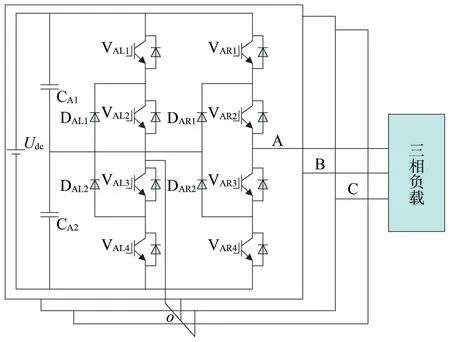
圖1 NPC/H橋五電平逆變器拓撲結構Fig.1 The topology of NPC/H bridge five-level inverter

多電平逆變器調制過程中，需要將各相輸出電平狀態解碼為各開關管的導通狀態。NPC/H 橋模塊的五種電平對應9 種開關狀態，即有解碼方式1×2 × 3×2×1=12 種。文中解碼方式的選擇考慮兩個約束條件：

1）NPC/H 橋模塊輸出狀態切換時，應避免左、右橋臂電平的跳變，優化動作開關次數。

2）合理分配開關切換方式，優化開關器件損耗均衡及電容電壓平衡。

為滿足以上兩個約束條件，表1、表2 分別給出兩種最優NPC/H 橋模塊解碼方式Ⅰ、Ⅱ。由于各器件開關狀態互補的情況，表1、表2 中僅給出了左橋臂VxL3、VxL4和右橋臂VxR1、VxR2的導通狀態。SxL、SxR為左、右橋臂電平狀態，Sx為x相輸出狀態，Sx=SxR-SxL，表1、表2 中器件開關狀態“1”為導通，“0”為關斷。

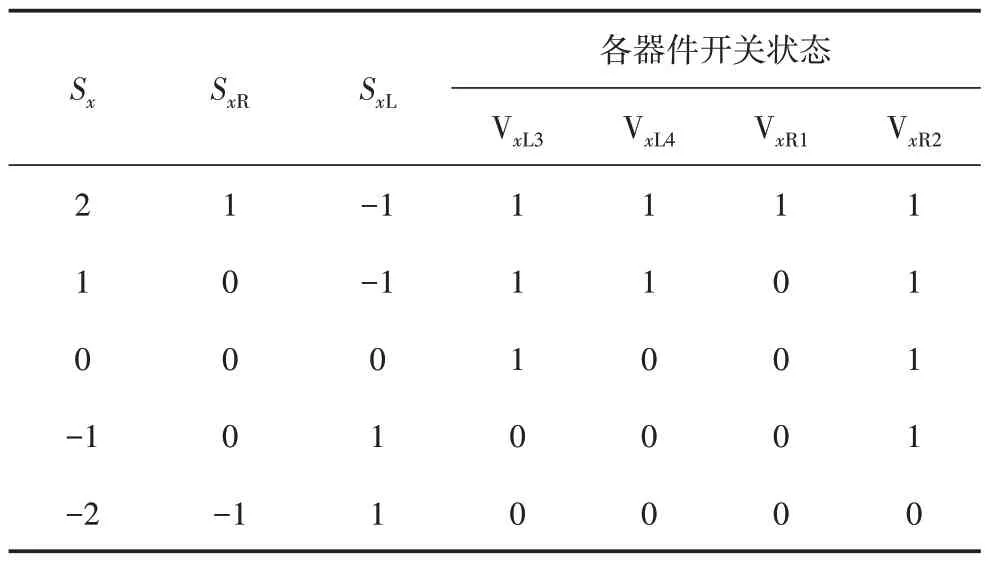
表1 NPC/H橋模塊的解碼方式ⅠTable 1 The decoderⅠfor NPC/H bridge module

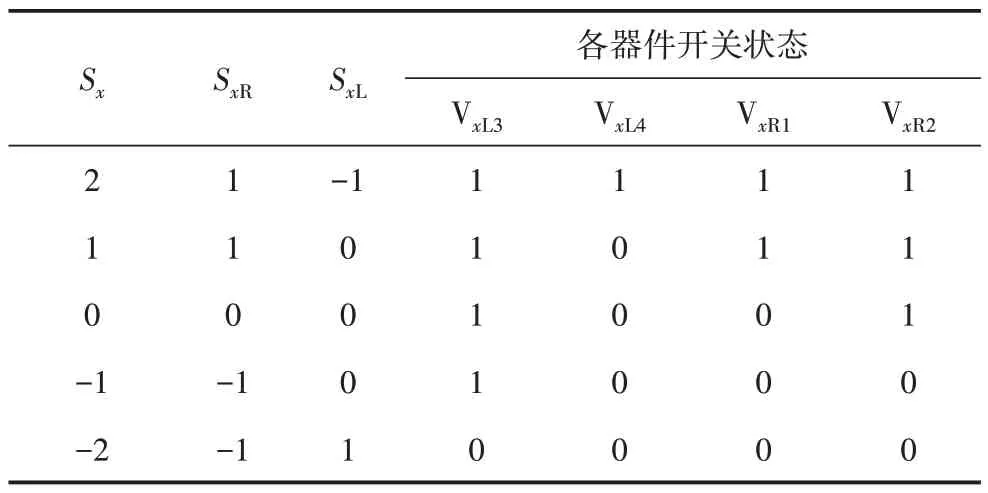
表2 NPC/H橋模塊的解碼方式ⅡTable 2 The decoderⅡfor NPC/H bridge module

2 基于g-h坐標系的三段式SVPWM算法

文獻［18-19］采用一種基于60°g-h坐標系的簡化調制算法，可以避免大量三角函數的計算。針對NPC/H 橋五電平逆變器，文中設計一種基于g-h坐標系的三段式SVPWM 算法。與七段式開關序列相比，在相同逆變器等效開關頻率下，三段式的平均開關次數更少，開關器件損耗更低。

2.1 坐標變換

非正交60°坐標系又稱g-h坐標系，g軸與三相坐標系abc的a軸重合，g軸逆時針旋轉60°為h軸。參考矢量在三相坐標系abc中的坐標分量為va、vb、vc，在g-h坐標系中的坐標分量設為vg、vh。根據兩種坐標系之間的幾何關系，可得坐標變換公式為

將abc坐標系中五電平電壓矢量的坐標經式（1）變換后，可得g-h坐標系下電壓矢量坐標，圖2為g-h坐標系中第Ⅰ扇區電壓矢量的坐標分量。圖2 中，在g-h坐標系下各基矢量的坐標值均為整數，便于計算，Vr為參考矢量，VE、VF、VP、VQ為距離參考矢量最近的四個基矢量，r、E、F、P、Q分別為參考矢量和四個基矢量在g-h坐標系中的終點。

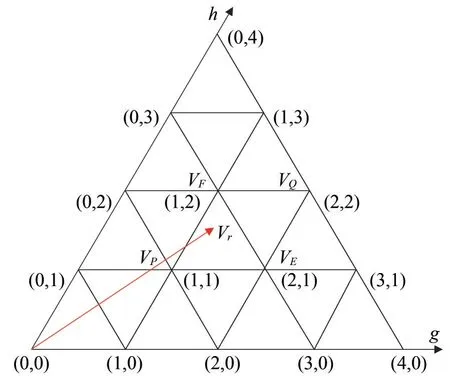
圖2 基于g-h坐標系第Ⅰ扇區電壓矢量的坐標分量Fig.2 The components of voltage vector in the first sector based on the g-h coordinate

2.2 確定基矢量

將坐標分量vg、vh向上取整或向下取整，可得到距離參考矢量最近的四個基矢量坐標，圖2 中參考矢量Vr對應的四個基矢量VE、VF、VP、VQ的坐標如式（2）所示。

式中：ceil（·）、floor（·）為函數，對括號內變量進行向上、向下取整。

VE、VF必定是距離Vr最近的兩個基矢量，第三個最近基矢量與Vr的終點位于對角線EF的同一側。為選擇VP或VQ，定義l=vg+vh-ceil(vg)-floor(vh)，l=0 時，參考矢量的終點在對角線EF上。當l≥0 時，選擇基矢量VQ；l＜0 時，選擇基矢量VP。以圖2 中參考矢量為例，求得最近的三個基矢量坐標分別為（2，1）、（1，2）、（1，1）。

根據距離Vr最近的三個基矢量的坐標值，可以獲得各基矢量對應的開關狀態。對于五電平逆變器，由式（3）獲得基矢量的開關狀態[SA,SB,SC]。

式中：Ug、Uh為基矢量的g-h坐標分量。

如圖2 所示，基矢量VP坐標為（1，1），共對應［2，1，0］，［1，0，-1］，［0，-1，-2］三種開關狀態，它們輸出電壓矢量的幅值和相位均一致。冗余開關狀態的存在，就需要選擇開關狀態和優化開關序列。

2.3 計算作用時間

已知合成Vr的三個基矢量后，可列其伏秒平衡方程，如式（4）所示。

式中：V1=VE、V2=VF、V3=VP或V3=VQ；d1、d2、d3分別為基矢量V1、V2、V3的占空比。

當V3=VP時，將參考矢量分別投影在g軸和h軸上，展開式（4），并與式（2）聯立可得

當V3=VQ時，同理可得

將占空比乘以開關周期即是基矢量的作用時間。

2.4 三段式開關序列

SVPWM 的三個頻率概念［20］：1）采樣頻率fsp等于采樣周期的倒數；2）器件平均開關頻率fda等于每秒全部開關管的開關次數除以器件數；3）逆變器等效開關頻率fcvt等于線電壓頻譜的第一邊帶諧波中心頻率，可以評估SVPWM 算法的諧波性能。

如圖2 參考矢量位于△EFP中，將△EFP稱為位矢三角形。在單個采樣周期1/fsp內，七段式SVPWM 采用四個開關狀態分成七段式開關序列，如圖3（a）所示；三段式SVPWM 采用三個開關狀態構成三段式開關序列，如圖3（b）所示。

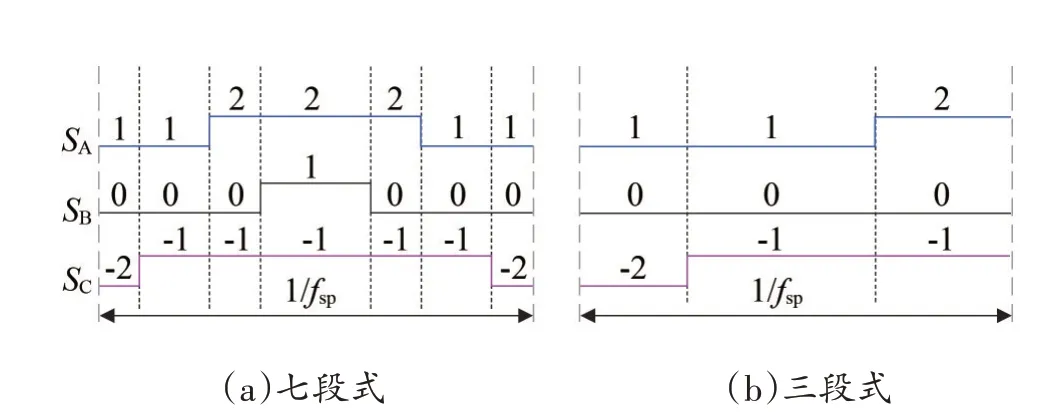
圖3 七段式和三段式開關序列Fig.3 7-segment and 3-segment switching sequences

根據圖3 可推測出逆變器的器件理想平均開關頻率fdai。單個采樣周期內，七段式開關序列中三相均有一次上升電平動作和一次下降電平動作，每相電平動作需要互補的2 個開關管動作（1 個導通、1個關斷）。開關管的導通和關斷合稱為1 次完整開關動作，NPC/H 橋五電平逆變器三相共有24 個開關器件，則七段式開關序列器件理想平均開關頻率fdai_7為

在單個采樣周期內，三段式開關序列只有兩相存在電平動作，如圖3（b）中A、C 相電平上升，B 相不變。動作相僅涉及一個開關器件導通和與其互補的開關器件關斷，則三段式開關序列的器件理想平均開關頻率為fdai_3。

由于相鄰采樣周期之間的開關狀態存在額外動作，器件實際平均開關頻率fdaa通常大于理想平均開關頻率fdai。

在單個采樣周期內，七段式開關序列每相含有一個完整的離散采樣，逆變器等效開關頻率fcvt_7為

三段式開關序列兩個采樣周期內有一次完整的離散采樣，其等效開關頻率fcvt_3為

理想狀態下，由式（9）和式（10）可見，器件平均開關頻率相等時，三段式的逆變器等效開關頻率比七段式高50%，負載諧波性能更好；同理，當逆變器等效開關頻率相同時，三段式的器件平均開關頻率比七段式低50%，器件開關損耗更低。

三段式開關序列選擇原理如下。考慮兩個相鄰采樣周期的狀態變化，定義第一個采樣周期的開關序列為［SA1，SB1，SC1］→［SA2，SB2，SC2］→［SA3，SB3，SC3］，第二個采樣周期的開關序列為［SA1'，SB1'，SC1'］→［SA2'，SB2'，SC2'］→［SA3'，SB3'，SC3'］。顯然，當第二個開關序列的首發狀態［SA1'，SB1'，SC1'］與第一個開關序列的末尾狀態［SA3，SB3，SC3］不同時，將產生額外開關動作。為減少額外開關動作，需要減小首發狀態［SA1'，SB1'，SC1'］與末尾狀態［SA3，SB3，SC3］的差異。根據上一采樣周期的末尾狀態［SA3，SB3，SC3］靈活選擇下一首發狀態［SA1'，SB1'，SC1'］，三段式開關序列的詳細設計方法如下。

1）選擇首發狀態。

定義任意開關狀態［SA，SB，SC］的狀態值S為

定義兩個表示開關狀態變化的參數，ΔS為三相開關狀態總變化值，δS為最大單相開關狀態變化值。

第二個采樣周期的首發狀態［SA1'，SB1'，SC1'］通過以下原則選擇：第1 步從可選擇開關狀態中，選擇ΔS最小的狀態，該原則可有效降低額外的開關動作，若存在多個狀態符合要求，則執行下一步；第2步選擇δS最小的開關狀態，該原則可抑制電平級數變化從而避免波形中不合理的電壓跳變，若仍有多個可選開關狀態，則執行下一步；第3 步選擇狀態值S最小的狀態完成首發狀態的選擇。

圖4（a）給出了一個根據上一末尾狀態選擇下一首發狀態的示例，TZ1至TZ16代表第Ⅰ扇區內16 個三角形區域，兩個相鄰采樣周期參考矢量從三角形TZ2移動至三角形TZ6。情況1：三角形TZ2中，三段式開關序列末尾狀態為［2，0，-1］，由第1 步可直接選出［2，1，-1］為三角形TZ6中的首發狀態。情況2：三角形TZ2的末尾狀態為［2，-1，-2］，由第1 步可選出［2，1，-2］、［1，0，-2］，進而根據第2 步可選出［1，0，-2］作為三角形TZ6的首發狀態。

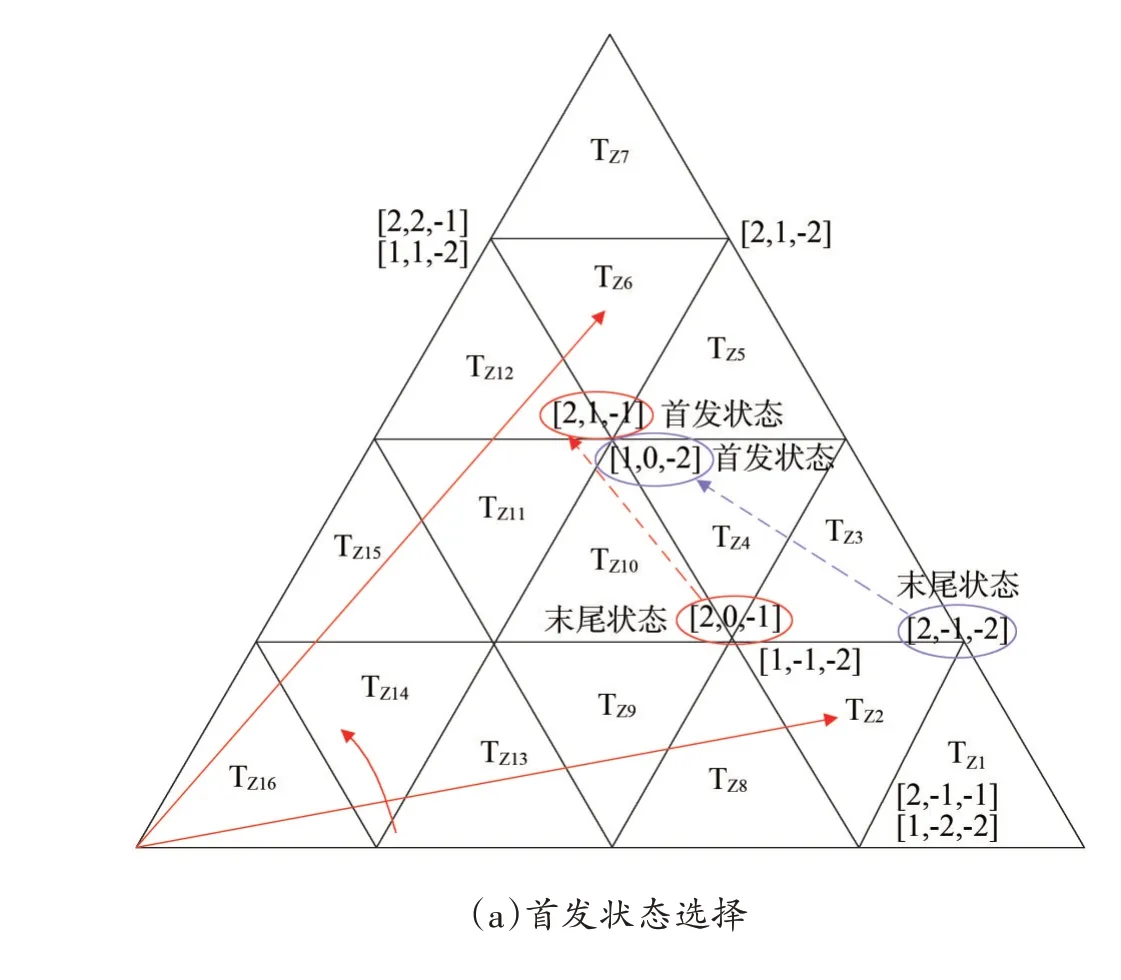
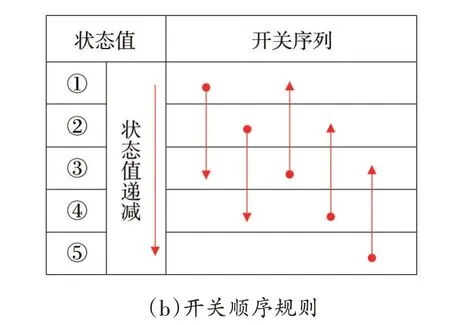
圖4 三段式開關序列的選擇原理Fig.4 The selecting principle of 3-segment switching sequence

2）安排開關順序。

根據狀態值S的大小，對三角形的開關狀態按照降序標記，標號為①—④或①—⑤（如三角形TZ1有四種狀態，三角形TZ2有五種狀態）。如圖4（a）中的三角形TZ2，狀態①對應［2，0，-1］，狀態⑤對應［1，-2，-2］。

圖4（b）為開關順序安排規則，圖中圓點為首發狀態［SA1，SB1，SC1］，箭頭穿過三個開關狀態，構成三段式開關序列。

如圖5 所示，以第Ⅰ扇區為例，當參考矢量經過最外層每個小三角形均有一個采樣點時，根據三段式開關序列選擇原理，各三角形的開關序列如下。

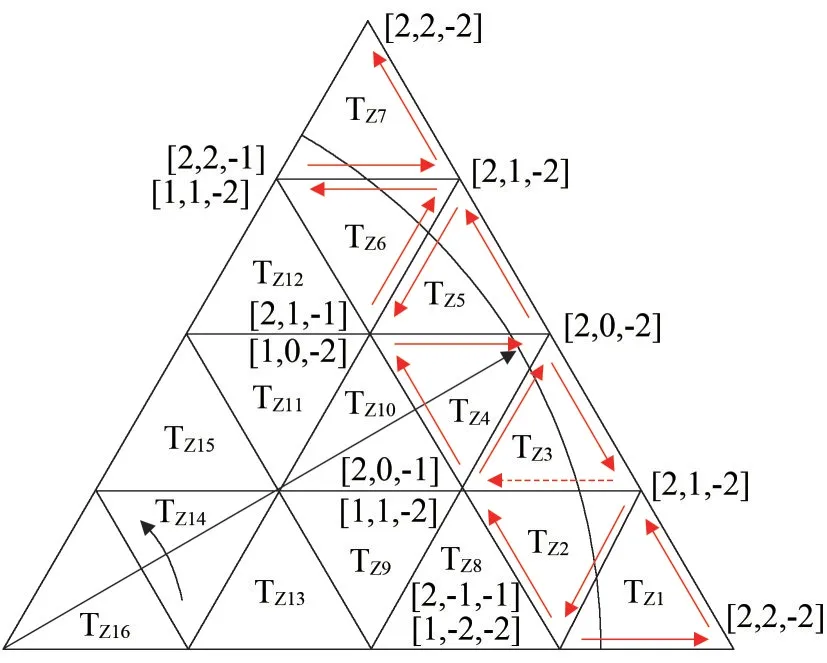
圖5 三段式開關序列示例Fig.5 Example of 3-segment switching sequences

三角形TZ1：［1，-2，-2］→［2，-2，-2］→［2，-1，-2］；

三角形TZ2：［2，-1，-2］→［2，-1，-1］→［2，0，-1］；

三角形TZ3：［2，0，-1］→［2，0，-2］→［2，-1，-2］；

三角形TZ4：［1，-1，-2］→［1，0，-2］→［2，0，-2］；

三角形TZ5：［2，0，-2］→［2，1，-2］→［2，1，-1］；

三角形TZ6：［2，1，-1］→［2，1，-2］→［1，1，-2］；

三角形TZ7：［1，1，-2］→［2，1，-2］→［2，2，-2］。

由圖5 可見，參考矢量在三角形邊界切換時，僅在三角形TZ3與三角形TZ4間切換時產生額外的開關動作（虛線箭頭狀態［2，-1，-2］切換至［1，-1，-2］存在電平變化），其他三角形間切換時無額外開關動作。

3）解碼開關狀態。

因為開關序列為數字編碼，需要根據表1、表2 中NPC/H 橋模塊的解碼方式將開關狀態解碼為各開關器件的導通或關斷信號，從而控制逆變器的輸出。

2.5 仿真分析

采用基于g-h坐標系的三段式SVPWM 算法，搭建NPC/H 橋五電平逆變器Simulink 仿真模型，以驗證該算法的有效性。仿真參數如表3 所示，圖6 為調制度m=0.9 時，三段式SVPWM 的仿真波形，圖中THD為總諧波畸變率（total harmonic distortion，THD）。

《意見稿》規定，寄件人有以下情形的，智能快件箱運營企業應當不予提供寄遞服務：未按照規定完成實名信息采集或未通過身份查驗的；未依法提供快遞運單有關信息的；未按照規定在寄遞記錄專用區域進行交寄操作的。

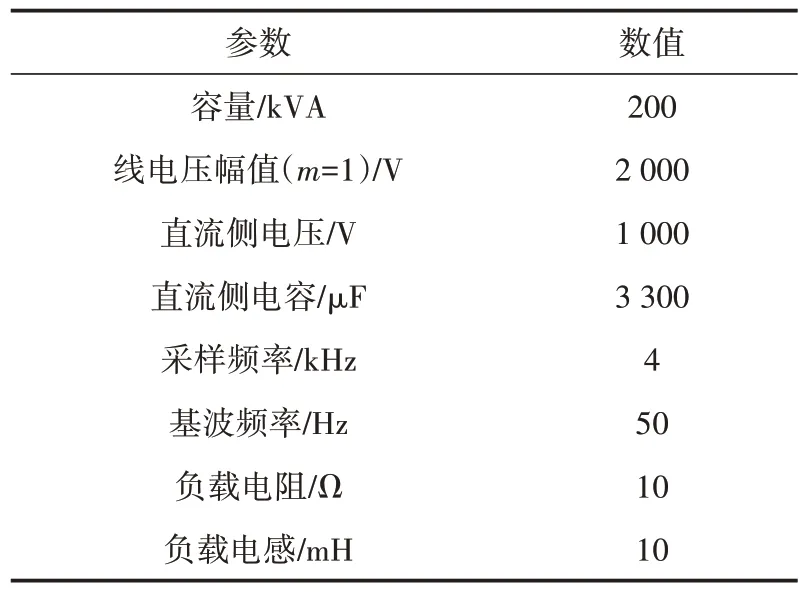
表3 仿真參數Table 3 The simulation parameters

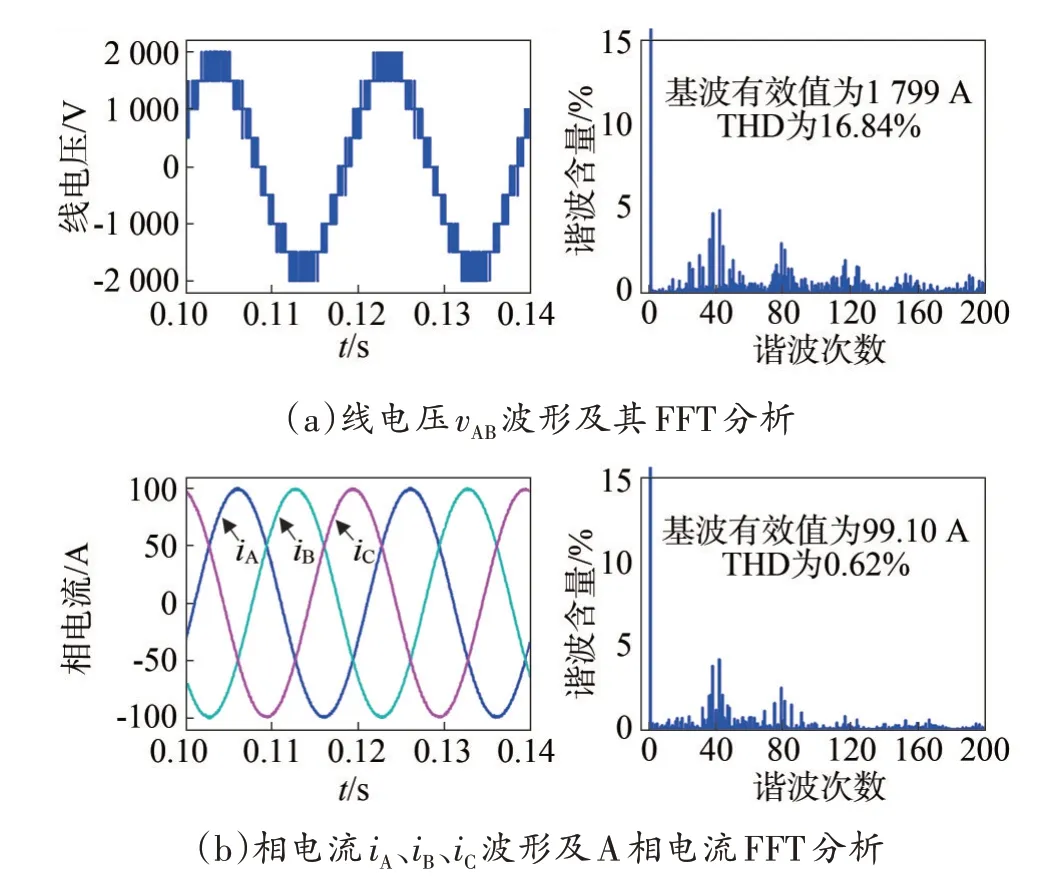
圖6 三段式SVPWM的仿真波形Fig.6 The simulation waveforms of 3-segment SVPWM

由圖6 中線電壓和相電流的快速傅里葉變換（fast fourier transformation，FFT）分析可知，逆變器的等效開關頻率為2 kHz，即為0.5fsp。三段式SVPWM線電壓和相電流的基波幅值分別為1 799 V、99.10 A，相電流的THD 為0.62%，逆變器的輸出能力較強，波形質量較好。

圖7 為不同調制度下三段式SVPWM 與七段式SVPWM 的器件實際平均開關頻率fdaa之間對比。逆變器等效開關頻率為2 kHz 時，三段式和七段式的器件理想平均開關頻率fdai分別為333 Hz、500 Hz。從圖7 可知，大部分調制區域內，兩種調制策略的fdaa均比fdai更大，該現象由三角形邊緣切換時的額外開關動作導致。三段式的fdaa比七段式低50%，驗證了三段式的開關損耗更低。

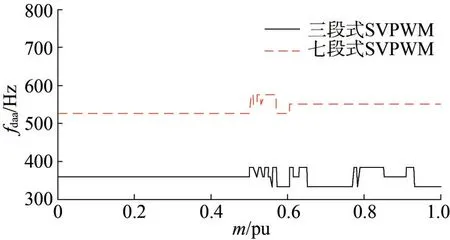
圖7 不同調制度下三段式SVPWM與七段式SVPWM的fdaa對比Fig.7 The comparison of fdaa between 3-segment SVPWM and 7-segment SVPWM

為驗證低開關頻率下三段式SVPWM 輸出THD較低的效果，圖8、圖9 分別給出了逆變器等效開關頻率fcvt為1 000 Hz、500 Hz 的仿真結果。

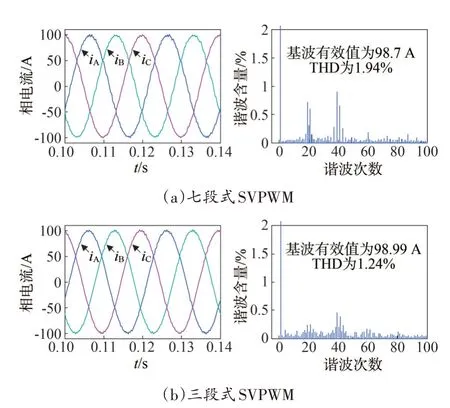
圖8 fcvt=1 000 Hz時相電流及其頻譜分析Fig.8 The phase currents and spectrum analysis of 3-seg and 7-seg SVPWM when fcvt=1 000 Hz

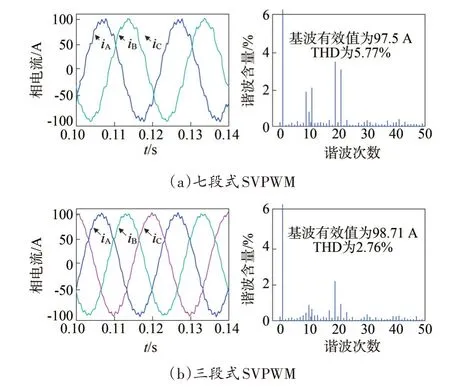
圖9 fcvt=500 Hz時相電流及其頻譜分析Fig.9 The phase currents and spectrum analysis of 3-seg and 7-seg SVPWM when fcvt=500 Hz

根據圖8、圖9 的仿真結果，可知開關頻率越低，七段式的輸出電流畸變越嚴重；三段式輸出電流波形仍具有較高的正弦度，波形質量優化較明顯。因此，低開關頻率工況下，逆變器適合采用三段式開關序列。

逆變器等效開關頻率fcvt為500 Hz 時，調制度m在0.1～1 變化，三段式SVPWM 與七段式SVPWM 相電流的THD 對比如圖10 所示，不同調制度下，三段式的相電流諧波質量均比七段式更好，調制度越高，優化效果越明顯。

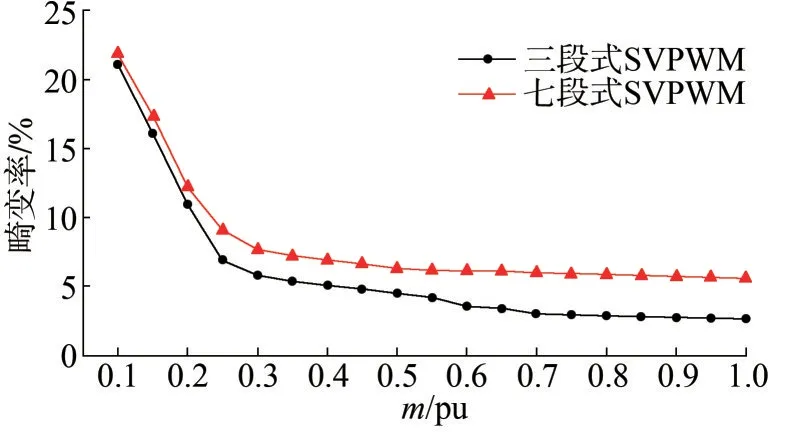
圖10 不同調制度下三段式與七段式SVPWM的相電流總畸變率對比Fig.10 The comparison of the phase current THD between 3-seg and 7-seg SVPWM

3 中點電位控制

關于NPC/H 橋五電平逆變器的中點電位平衡問題，需要根據電流方向和電容電壓差，在逆變器輸出電平為±Udc/2 時，合理選擇SxL、SxR組合，從而抑制電容電壓偏移，平衡中點電位。

以A 相為例，詳細分析vAo=Udc/2 時不同開關狀態和電流方向對電容電壓的影響，如圖11 所示。

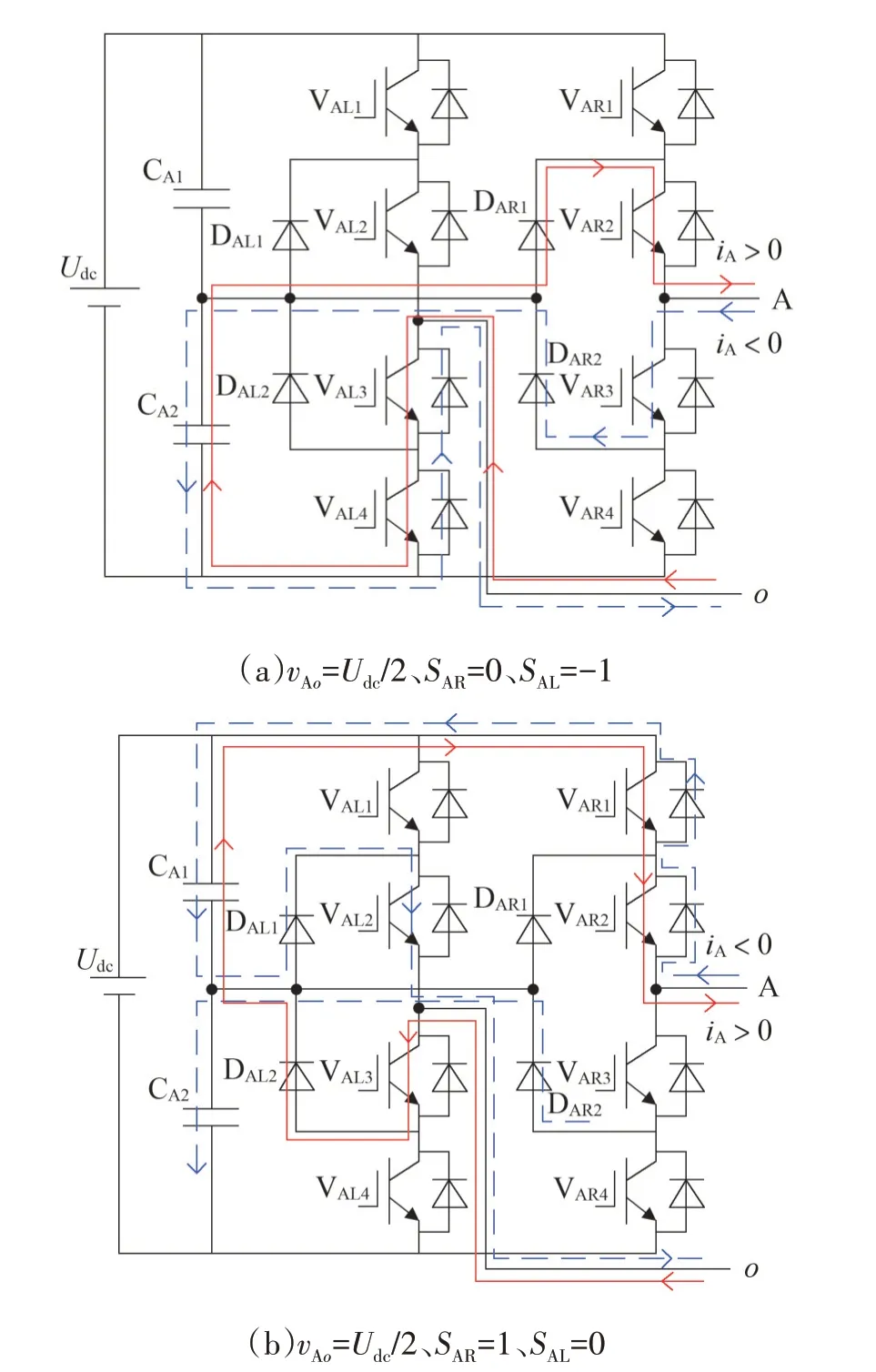
圖11 vAo=Udc/2 時不同開關狀態和電流方向對電容電壓的影響Fig.11 Impactsofdifferentswitchingstatesandthedirections ofphasecurrentoncapacitorvoltageswhen vAo=Udc/2

圖11（a）中，vAo=Udc/2、SAR=0、SAL=-1，器件VAR2、VAR3、VAL3、VAL4導通。當iA＞0 時，電流路徑為：o點→VAL3、VAL4→CA2→DAR1→VAR2→A 相負載，則電容CA2放電，由于直流側為恒壓源，相應的CA1充電。當iA＜0時，電流路徑為：A 相負載→VAR3→DAR2→CA2→VAL3、VAL4的反并聯二極管→o點，則電容CA2充電，相應的CA1放電。

與vAo=Udc/2 時同理分析，可知vAo=-Udc/2 時不同開關狀態和電流方向對電容電壓的影響。總結以上分析，當逆變器輸出±Udc/2 時，左、右橋臂采用不同開關組合及電流方向對兩電容電壓的影響，如表4。由表4 可知，直流側兩均壓電容電壓波動，僅與單個NPC/H 模塊輸出±Udc/2 時左、右橋臂開關狀態和模塊電流方向有關，調制度和功率因素的變化不會影響NPC/H 橋電容中點控制方法的效果。

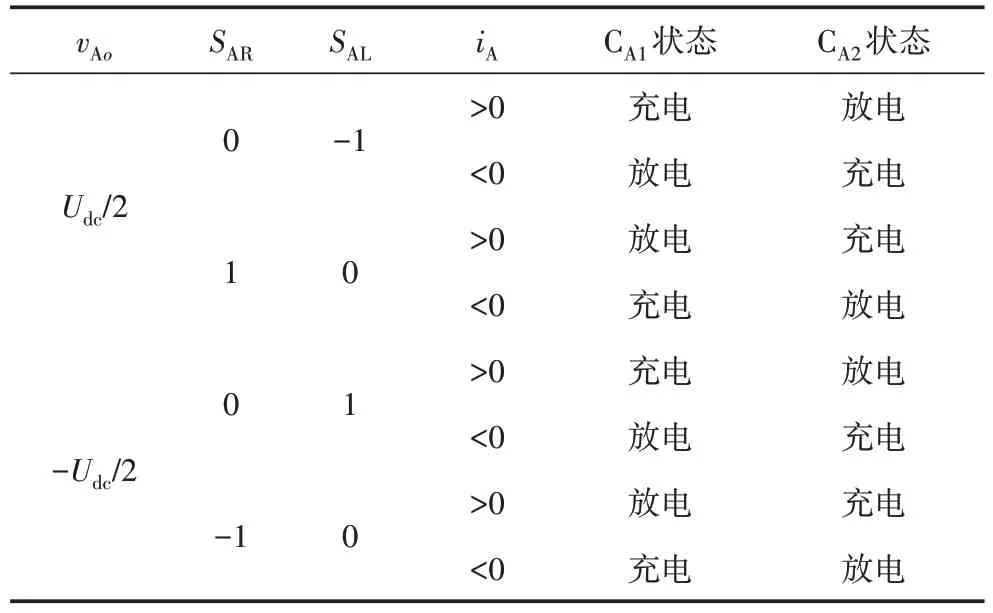
表4 不同開關狀態和電流方向下電容電壓的變化Table 4 The behaviors of capacitor voltages under different switching states and the directions of current

若不對直流側電容電壓進行控制，中點電位將發生偏移。為控制電容電壓，首先定義電容電壓差ΔUC為

式中：UCA1、UCA2為電容CA1、CA2的電壓。

為平衡中點電位，需要控制ΔUC趨于零。若ΔUC＞0，需要電容CA1放電，電容CA2充電；若ΔUC＜0，需要電容CA1充電，電容CA2放電。根據表4 可知，當iA＞0 時，若逆變器輸出vAo=Udc/2，左、右橋臂狀態選擇SAL=0、SAR=1 利于中點電位平衡；若逆變器輸出vAo=-Udc/2，左、右橋臂狀態選擇SAL=0、SAR=-1 利于中點電位平衡。該選擇與表2 解碼方式Ⅱ中Sx=±1 時，左、右橋臂SxL、SxR組合相同，因此ΔUC＞0 且iA＞0 時，NPC/H 橋模塊選擇解碼方式Ⅱ解碼。同理，其他情況下，平衡電容電壓解碼方式選擇如表5所示。

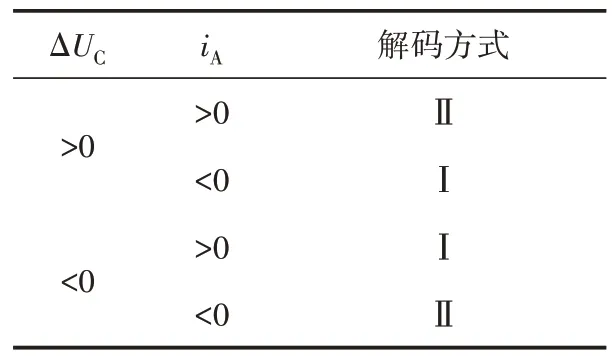
表5 平衡電容電壓解碼方式選擇表Table 5 The decoding schemes table for balancing capacitor voltages

基于SVPWM 算法搭建仿真模型驗證中點電位控制策略的有效性，仿真參數同表3，調制度m=0.9。圖12 為加入中點電位控制前后直流側電容電壓波形。從圖12（a）可見，控制前，三相六個直流側電容的電壓均在470～530 V 之間波動；加入控制后，電容電壓很快穩定。圖12（b）為A 相兩電容電壓波形局部放大圖，可見控制前UCA1波形基本在UCA2的下面，中點電位存在偏移；加入控制后，電壓UCA1與UCA2的波形基本重合，中點電位平衡。

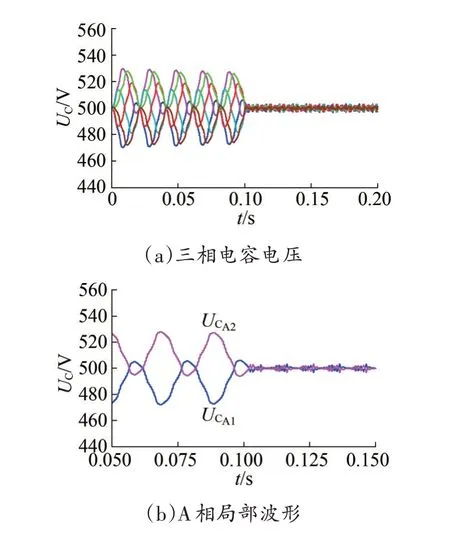
圖12 直流側電容電壓仿真結果Fig.12 The simulation results of DC capacitor voltages

4 實驗分析

基于數字信號處理器和現場可編程門陣列（digital singnal processor and field-programmable gate array，DSP&FPGA）聯合控制結構搭建NPC/H 橋五電平逆變器實驗平臺，硬件電路為串聯型12 脈波不控整流器和NPC/H 橋五電平逆變器構成的交直交變頻系統，逆變器帶三相對稱阻感負載，實驗參數如表6 所示。

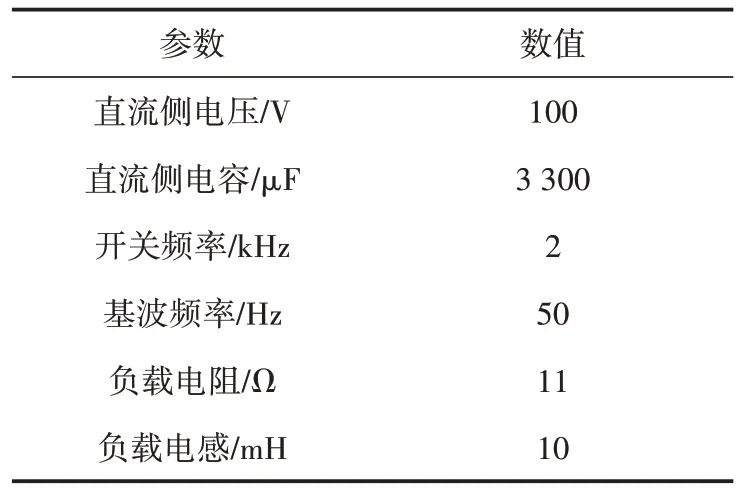
表6 實驗參數Table 6 The experimental parameters

為驗證三段式SVPWM 在低開關頻率下的優勢，選取等效開關頻率fcvt為1 000 Hz、500 Hz，調制度m=0.85 時，逆變器A 相輸出電流波形及其頻譜分析如圖13、圖14 所示。

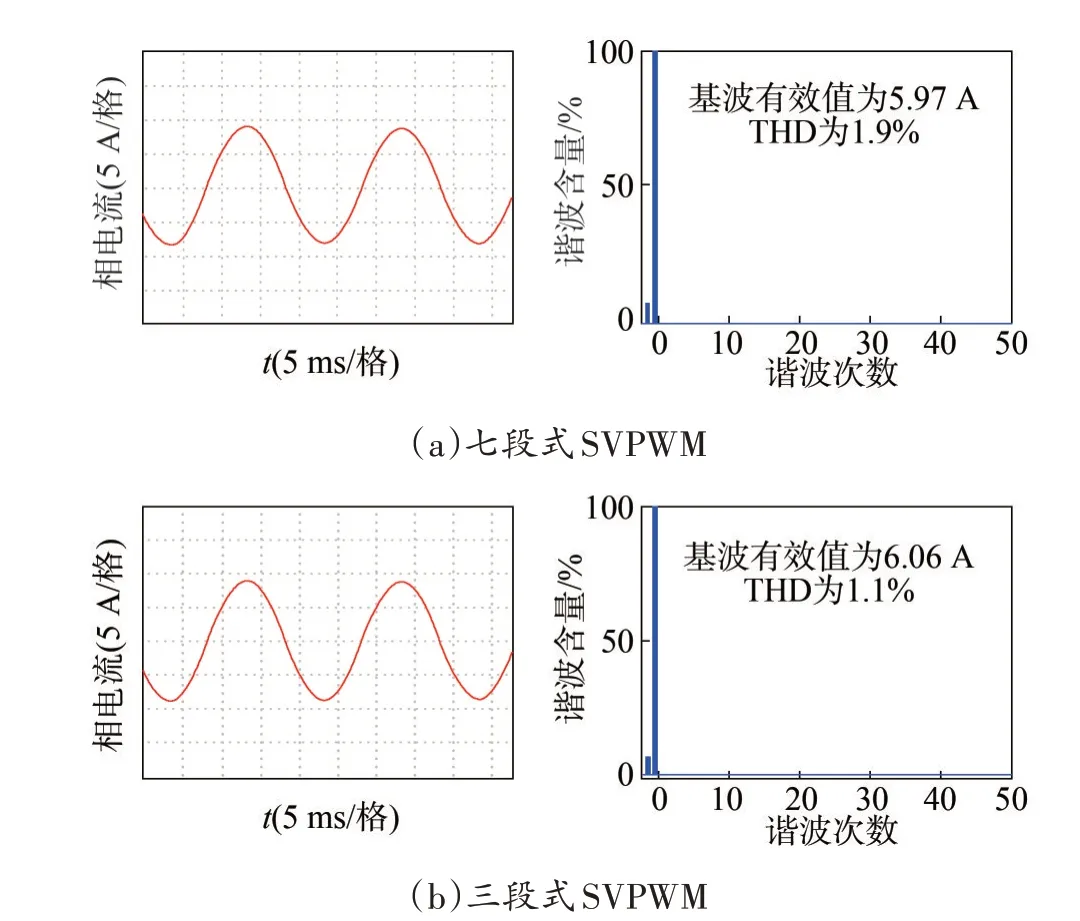
圖13 fcvt=1 000 Hz時七段式、三段式SVPWM相電流及其頻譜圖Fig.13 The phase currents and spectrum of 3-seg and 7-seg SVPWM when fcvt=1 000 Hz

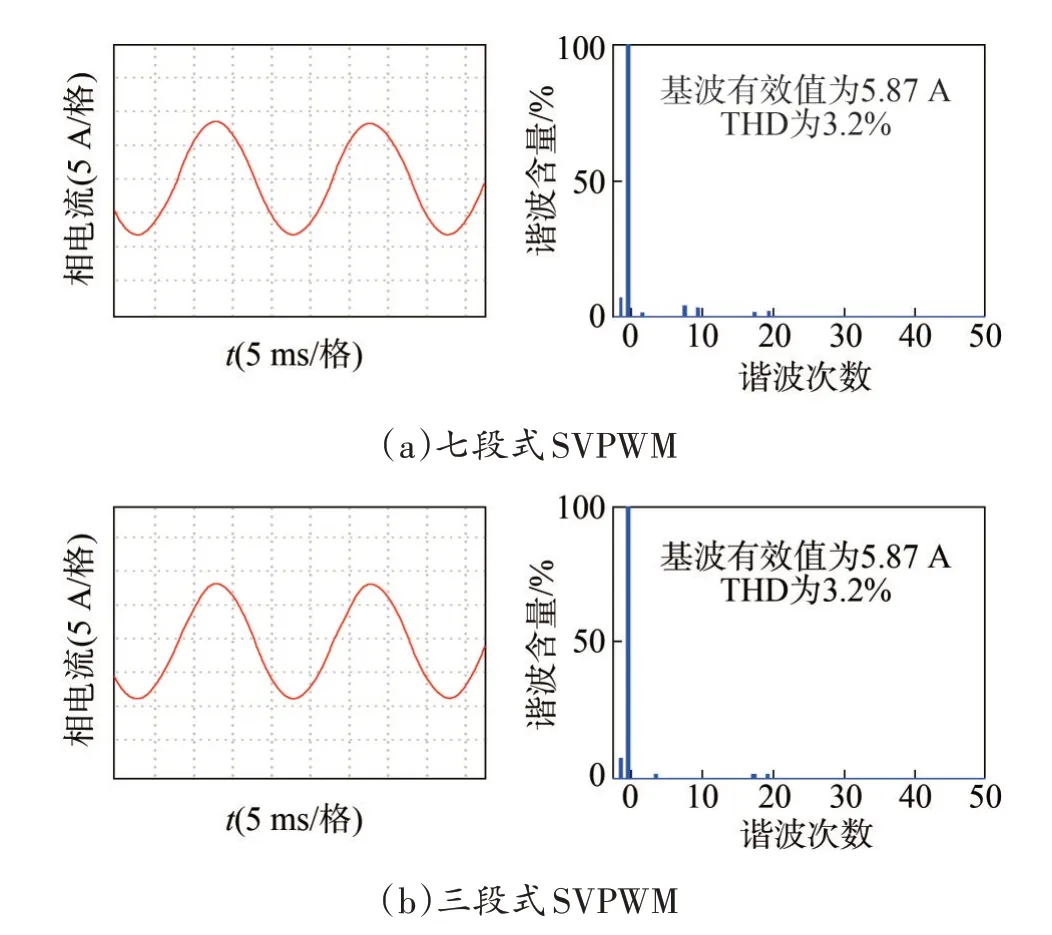
圖14 fcvt=500 Hz時七段式、三段式SVPWM相電流及其頻譜圖Fig.14 The phase currents and spectrum of 3-seg and 7-seg SVPWM when fcvt=500 Hz

圖13 中，等效開關頻率fcvt=1 000 Hz 時，七段式SVPWM 輸出相電流的基波有效值為5.97 A、THD 為1.9%；三段式SVPWM 輸出相電流的基波有效值升高為6.06 A、THD 降低為1.1%。圖14 中，等效開關頻率fcvt=500 Hz 時，七段式SVPWM 輸出相電流波形可以看到明顯畸變；三段式SVPWM 的相電流波形正弦性較好，電流的基波有效值由5.72 A 升至5.87 A、THD 由5.3%降至3.2%。

實驗分析可知，等效開關頻率相同時，三段式SVPWM 的逆變器輸出電流能力更高，諧波性能也更好。驗證了三段式SVPWM 在低開關頻率的運行狀態下優勢明顯。

為驗證基于SVPWM 算法的中點電位平衡控制的有效性，以A 相為例，在運行一段時間后，加入中點電位控制，直流側兩電容電壓實驗波形如圖15 所示。波形圖上半部分為UCA1、UCA2電壓波形，下半部分為ΔUC=UCA1-UCA2。由實驗波形可見，中點控制前，兩電容電壓波形上下交替，兩電容電壓之差ΔUC在-5～5 V 波動；加入中點控制后，中點電位很快穩定在50 V 附近，兩電容電壓波形基本重合，兩電容電壓之差ΔUC在-1～1 V 波動。實驗結果驗證了根據電壓偏差和電流方向合理選擇左、右橋臂開關狀態平衡中點電位方法的有效性。

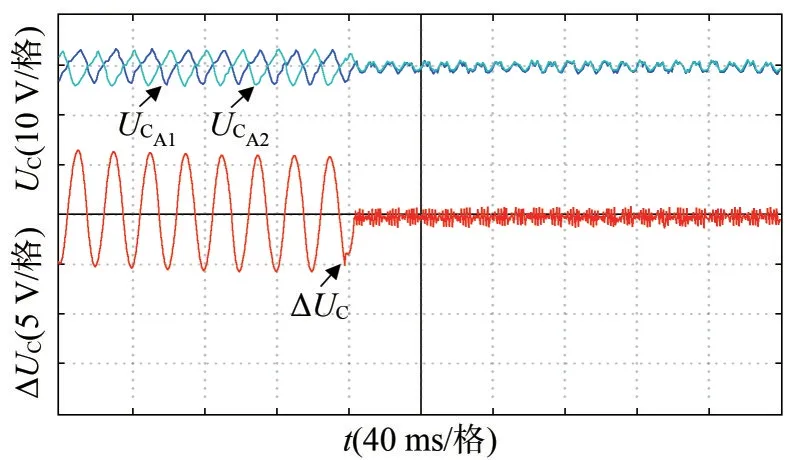
圖15 直流側電容電壓實驗波形Fig.15 The experimental waveform of DC capacitor voltages

5 結束語

針對NPC/H 橋五電平逆變器，基于g-h坐標系設計一種三段式SVPWM 開關序列，相同等效開關頻率的情況下，三段式開關序列比七段式的器件平均開關頻率低，輸出能力更高，諧波性能更好。進一步分析了NPC/H 橋模塊的直流側電容電壓波動原因，基于三段式SVPWM 算法，根據電流方向和電容電壓差，合理選擇NPC/H 橋模塊解碼方式，平衡直流側電容中點電位。通過仿真和實驗平臺驗證了三段式SVPWM 和中點電位控制方法的有效性。