基于廣義諧振理論的輸電線路無源干擾諧振頻率求解

漆 照，劉傳彬，李丹丹，沈 浩，馬國慶

（1.山東中實易通集團有限公司，山東 濟南，250003；2.國網山東省電力公司電力科學研究院，山東 濟南，250003；3.國網山東省電力公司，山東 濟南，250000）

0 引言

在國家新基礎設施建設的背景下，輸電線路對周邊無線電臺站的無源干擾現象越來越嚴重［1-2］。根據現有研究成果，獲取干擾諧振頻率，從而制定防護距離是解決輸電線路無源干擾的關鍵［3-5］。然而，由于環境和特高壓輸電線路路徑的復雜性，加之無線電臺站允許的干擾水平不一致，很難通過實驗方法確定諧振頻率。

輸電線路無源干擾問題主要研究模型為電場積分方程［6-7］，由于電場積分方程涉及大量積分運算，主要采用矩量法［8-10］對其進行離散求解。1996年，IEEE 在Trueman C.W.和Tilston M.A.等人［11-12］的研究基礎上，根據天線理論［13］，提出中波頻段（0.535～1.705 MHz）輸電線路無源干擾水平極值的預測方法，即“整數倍波長回路諧振頻率”和“四分之一波長諧振頻率”，上述方法忽略了鐵塔的細節，僅以細導線代替鐵塔整體。當頻率超過1.7 MHz 時，根據文獻［3，14］研究結論，鐵塔的角鋼、輔材都將影響輸電線路在外界激勵下的電磁散射，即鐵塔細節變得不可忽略。因此，IEEE 明確指出其方法僅適用于1.7 MHz 以下頻率的無源干擾諧振頻率預測。文獻［15］基于矩量法研究輸電線路的無源干擾，證實在1.7 MHz 以上仍然存在明顯的干擾諧振現象。然而，由于缺乏相應的理論，針對1.7 MHz 無源干擾諧振問題，截至當前，仍只能依靠矩量法進行掃頻計算，從而獲得觀測點處的無源干擾極值。采用矩量法掃頻計算確定干擾極值時，必須改變計算條件多次進行計算，從而造成計算量過大等問題。

針對上述問題，采用系統函數的思想，研究輸電線路與無線電臺站構成系統整體的電磁散射特性，從而將研究多天線系統的廣義諧振理論［16-17］引入大尺寸的輸電線路無源干擾研究中。通過少量頻點的散射場強信息即可構建出系統整體的系統函數，并求解輸電線路無源干擾的諧振頻率。

1 輸電線路無源干擾產生機理及其諧振頻率求解方法

1.1 輸電線路無源干擾產生機理

廣域空間下的輸電線路輸電距離長達幾十到幾百千米不等，在某些情況下，將不可避免地穿越各類無線電臺站信號所覆蓋的區域。此時，無線電臺站發射的入射電磁波與輸電線路金屬結構中的帶電粒子相互作用，從而在輸電線路表面產生與入射電磁波同頻的感應電流，使輸電線路被動地向附近空間輻射電磁波。該輻射電磁波與原入射電磁波疊加，改變原入射波的幅值和相位，對無線電臺站的信號發射或接收產生干擾，即無源干擾。輸電線路對無線電臺站無源干擾如圖1 所示。

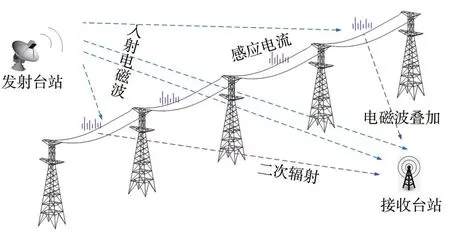
圖1 輸電線路對無線電臺站無源干擾Fig.1 Schematic diagram of passive interference from power transmission lines to radio stations

1.2 現有的諧振頻率求解方法

輸電線路無源干擾計算主要采用矩量法。計算輸電線路無源干擾的簡化模型如圖2 所示。圖中有2 個坐標系，即直角坐標系(x,y,z) 和球坐標系(r,θ,φ)，電磁波Ei以入射角(θi,φi)照射到輸電線路上；Es為觀測點P處的散射場強。為獲取輸電線路表面的感應電流，而后獲取任意觀測點的散射場強，須建立聯系輸電線路表面感應電流和入射場強之間的電場積分方程。

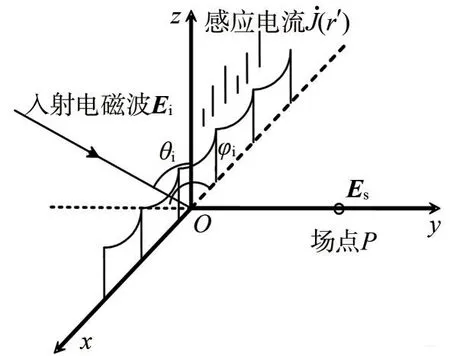
圖2 輸電線路無源干擾求解模型Fig.2 Passive interference solution model for power transmission lines

根據電磁場的基本理論，空間任意一點的散射場強可表示為

式中：ω為入射電磁波角頻率；μ為磁導率；k=為自由空間的波數，其中，ε 為自由空間的介電常數；?為哈密頓算子；為格林函數，其中，r'和r分別為源點和場點所在的位置；(r')為感應電流；Sd為輸電線路表面積分域。

由理想金屬導體表面切向電場為0 的邊界條件，可得

式中：“tan”表示取切向分量。

將式（1）代入式（2）可得

式（3）即為聯系輸電線路表面感應電流與入射電場的電場積分方程，由于式（3）涉及大量積分運算，感應電流(r')的求解過程困難。一般采用矩量法，將輸電線路劃分為若干單元，即對感應電流作離散處理，從而將式（3）的積分方程轉化為矩陣方程。根據每個剖分單元的感應電流在觀測點處散射場強的疊加，即可獲取任意位置的散射場強Es(r)。

求解干擾極值的過程中，在無線電臺站工作頻段內，通常先選定若干固定的θi值，而后在［0°，360°］等間隔改變φi取值，從而改變Ei的入射方向，以獲取圖2 中觀測點P處散射場強Es(r)的最大值。顯然，此方法為離散化求解，需要進行大量的掃頻計算。當入射電磁波頻率更高或線路結構更復雜時，消耗的計算資源更多，甚至出現無法求解的情況，且該方法只停留在定性分析無源干擾水平階段。

2 基于廣義諧振的輸電線路無源干擾諧振頻率求解

2.1 輸電線路無源干擾的廣義諧振頻率及Q值

文獻［16-17］在對飛機、船舶等電大尺寸散射體進行研究時，發現在某些特定頻率下，存在目標散射體的電磁散射突然增強的現象，將其定義為廣義諧振；從傳輸線理論、廣義諧振腔理論等方面對其進行深入研究，推導出廣義Foster 定理［18］與廣義諧振條件的計算公式。該理論針對的是以線天線為對象的多天線系統在近場區的諧振現象，但可將其理論方法和相關結論發展到同樣處于開放空間的輸電線路無源干擾諧振頻率研究中。

由坡印廷定理可知，對于任意封閉曲面S所包圍的空間體積為V的電磁系統，假設其外法線單位向量為，可得系統的復功率平衡表達式為

式中：σ為電導率，為空間函數；α為衰減因子；E為遠場區的電場場強；E*為遠場區電場場強的共軛；H為遠場區的磁場場強；H*為遠場區磁場場強的共軛。

考慮輸電線路和無線電臺站組成的電磁開放系統如圖3 所示。圖3 中，Sp為第p個天線覆蓋區域的表面積，vp為第p個天線覆蓋區域表面所包圍的區域，N為天線總個數，v'為輸電線路表面Sd所包圍的區域。

假設輸電線路和無線電臺站構成封閉曲面Se，曲面Se包含的空間體積為Ve，如圖3 所示。在無源區（Sd區），采用坡印廷定理有如下表達式：

在空間無窮遠處，即Ve=V∞時，坡印廷矢量虛部為零，則從電磁能量的角度可以認為式（4）和式（5）具有相同的物理含義。因此，可將輸電線路金屬陣列、無線電臺站視為統一整體，引入系統函數的概念，從而應用系統函數的零極點來預測系統的諧振頻率。當系統諧振時，式（5）中等式右邊最后一項為零。

輸電線路構成的金屬陣列，可以看作有耗的電磁系統，設其損耗為Ploss，根據復頻率理論，引入復頻率=ω0(1+jδ)，其中，ω0為系統的諧振頻率，δ為損耗因子，根據系統中能量的衰減特征，其損耗為

式中：W為t時刻系統諧振時存儲的平均能量。

諧振系統品質因數Q值為

可得

通過以上推導，能夠將輸電線路無源干擾諧振頻率與Q值一一對應起來。根據文獻［16］中的結論，當諧振頻率所對應得Q值足夠大時，輸電線路無源干擾才表現出較強的諧振，即干擾水平較高，可據此篩選掉不明顯的諧振極點。

2.2 輸電線路無源干擾的系統函數及諧振頻率求解

上文中，基于廣義諧振理論，引入輸電線路無源干擾系統函數的概念。假設系統函數為E(s)，并在復頻域中展開。

式中：O(s)、I(s)分別為系統函數在復頻域對應的輸入與輸出；E(s)為觀測點處的散射場強的復數表示形式，即E(s)=| |Es(r) ejφ(r)，其中，φ(r)為Es(r)對應的相位；a0、a1、a2、…am和b0、b1、b2、…bn分別為將系統函數在復頻域用Padé 有理函數展開后分子和分母多項式的系數；s=jωˉ為復頻率；m和n分別為系統函數E(s)分子分母的最高次項，決定待求系數a、b數量。上述系數可由模型參數估計［19-20］插值計算方法獲得。在MATLAB 中采用roots 函數直接求解系統函數分母多項式的根，即為系統函數對應的極點。其中穩定的極點（在復頻域左半部分的極點）對應于輸電線路可能的無源干擾諧振頻率。

2.3 算例分析

2.3.1 廣播天線激勵下的無源干擾

基于IEEE 提供的0.535～1.705 MHz 頻段廣播天線激勵的9 基鐵塔輸電線路的無源干擾模型，本文在電磁仿真軟件FEKO 中建立考慮鐵塔細節的仿真模型，如圖4 所示。其中，輸電線路鐵塔高為50.9 m，檔距為274 m。

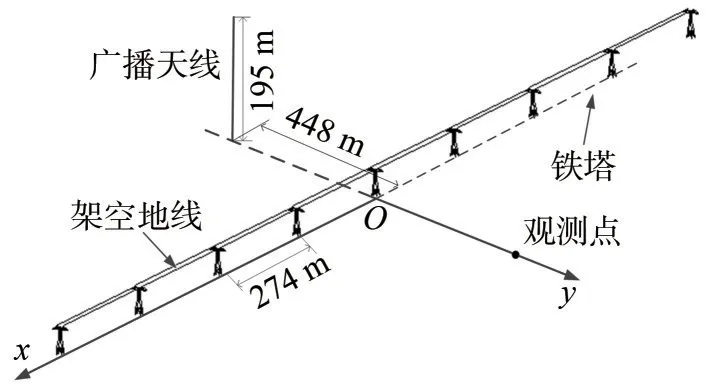
圖4 輸電線路無源干擾仿真模型Fig.4 Simulation model of passive interference for power transmission lines

廣播天線高為195 m，距離輸電線路中心448 m。天線饋電電壓為1 V，位于地面上。仿真頻率范圍為［0.53 MHz，3.20 MHz］，采樣點間隔為0.12 MHz，共有采樣點23 個。采用矩量法計算觀測點P（0，2 000 m，0）處的場強信息。

根據采樣點的場強信息，包括場強幅值和相位，通過模型參數估計插值方法計算式（9）中的系數a0、a1、a2…、am和b0、b1、b2…、bn，從而獲取系統函數，并計算其極點。根據廣義諧振理論獲取諧振頻率及Q值。在初步移除不穩定極點后，相關參數如表1 所示。

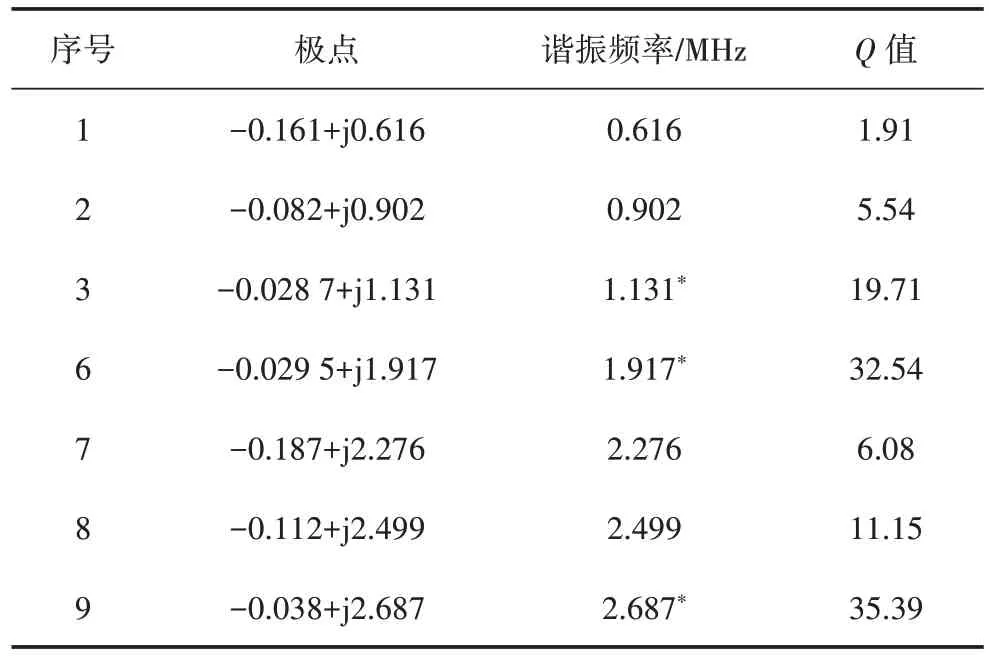
表1 無源干擾諧振頻率計算結果Table 1 Calculation results of passive interference under different resonance frequencies

根據廣義諧振理論，只有當Q值足夠大時，才有較強的諧振特性。因此，可以確定頻率為1.131 MHz、1.917 MHz、2.687 MHz，即第3 個、第6 個和第9 個極點對應輸電線路的無源干擾諧振頻率，如表1 中的“*”所示。

為驗證方法的準確性，將本文方法的預測結果與IEEE 模型的預測值進行比較。在考慮地線的情況下，IEEE 諧振頻率為［11］

式中：c為光速；h為塔高；d為檔距；M為正整數。

在0.535～1.7 MHz 頻段內，根據式（10）計算的諧振頻率為0.431 MHz、0.862 MHz、1.293 MHz。與表1 中本文方法預測的諧振頻率對比，可以發現，在1.7 MHz 以下，本文方法僅在1.131 MHz 時出現干擾諧振，且與IEEE 的預測結果有一定偏差。這可歸因于仿真中采用了更精細的模型，并從能量角度消除了不明顯的諧振點（即忽略了0.606 MHz 與0.902 MHz 的諧振頻率）。

在0.535～3.2 MHz 頻帶內，本文方法預測的結果與矩量法掃頻計算結果如圖5 所示。顯然，兩者的結果一致，第2 個干擾峰值處的最大偏差約為3%。

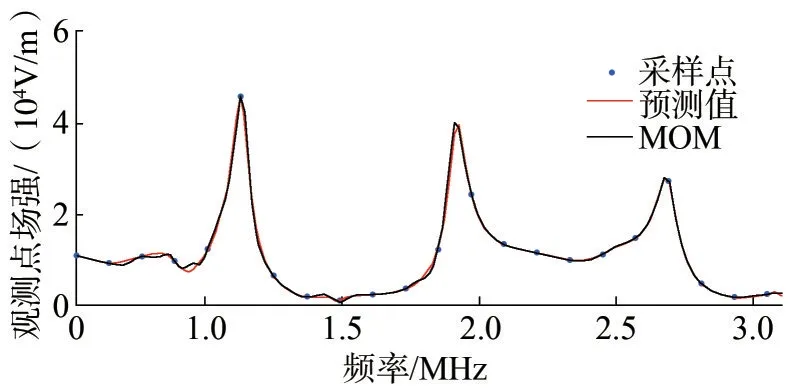
圖5 廣播天線激勵下散射場強Fig.5 Scattering field strength excited by broadcast antenna

為了分析采樣點對預測結果的影響，選擇17 個采樣點，即采樣間隔為0.15 MHz，預測無源干擾諧振頻率，相關參數如表2 所示。

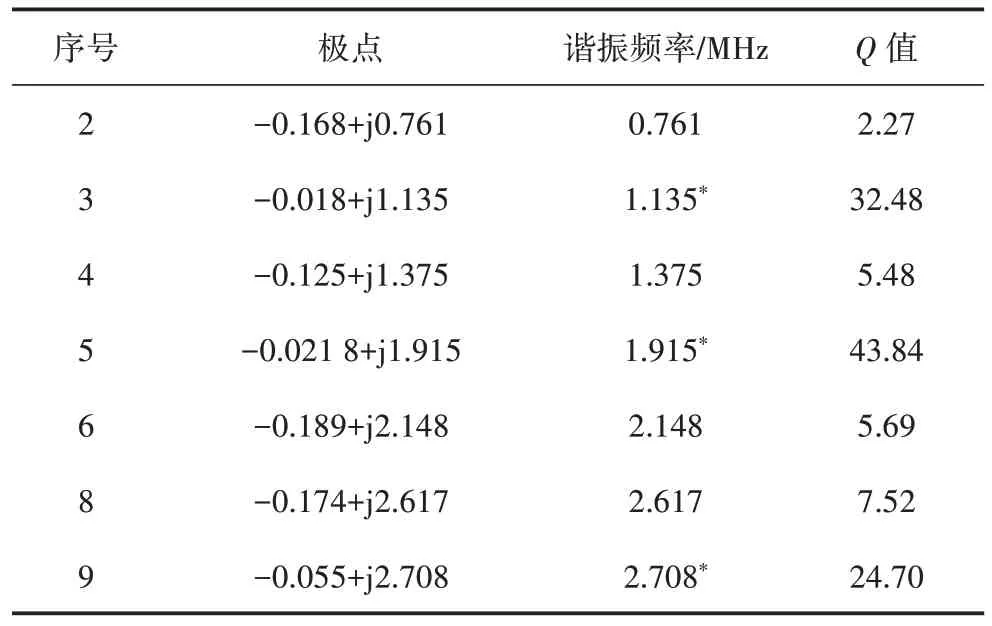
表2 無源干擾諧振頻率計算結果Table 2 Calculation results of passive interference under different resonance frequencies 單位：MHz

與表1 中的計算結果相比，可以發現采樣點的變化導致計算結果有一定偏差，但可以保證系統的真實諧振頻率不變。因此，通過適當選擇采樣點，可以較準確地獲得無源干擾的諧振頻率。

為了更直觀地展示輸電線路在廣播天線照射下的近場分布情況，繪制3 個諧振頻率下的輸電線路近場云圖如圖6 所示，繪制3 個非諧振頻率下的輸電線路近場云圖如圖7 所示。

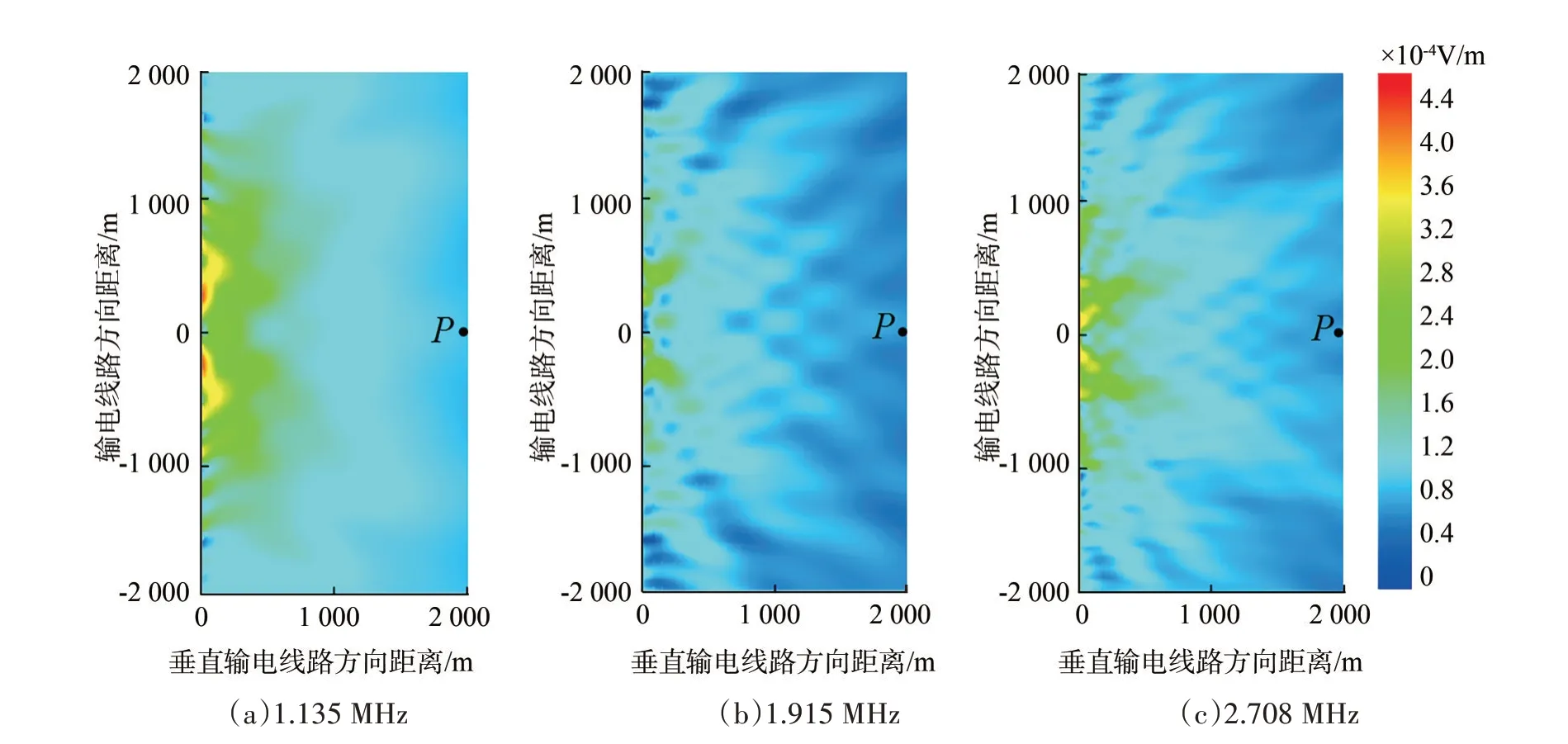
圖6 諧振頻率下的輸電線路近場云圖Fig.6 Near-field nephogram of power transmission lines at resonance frequency

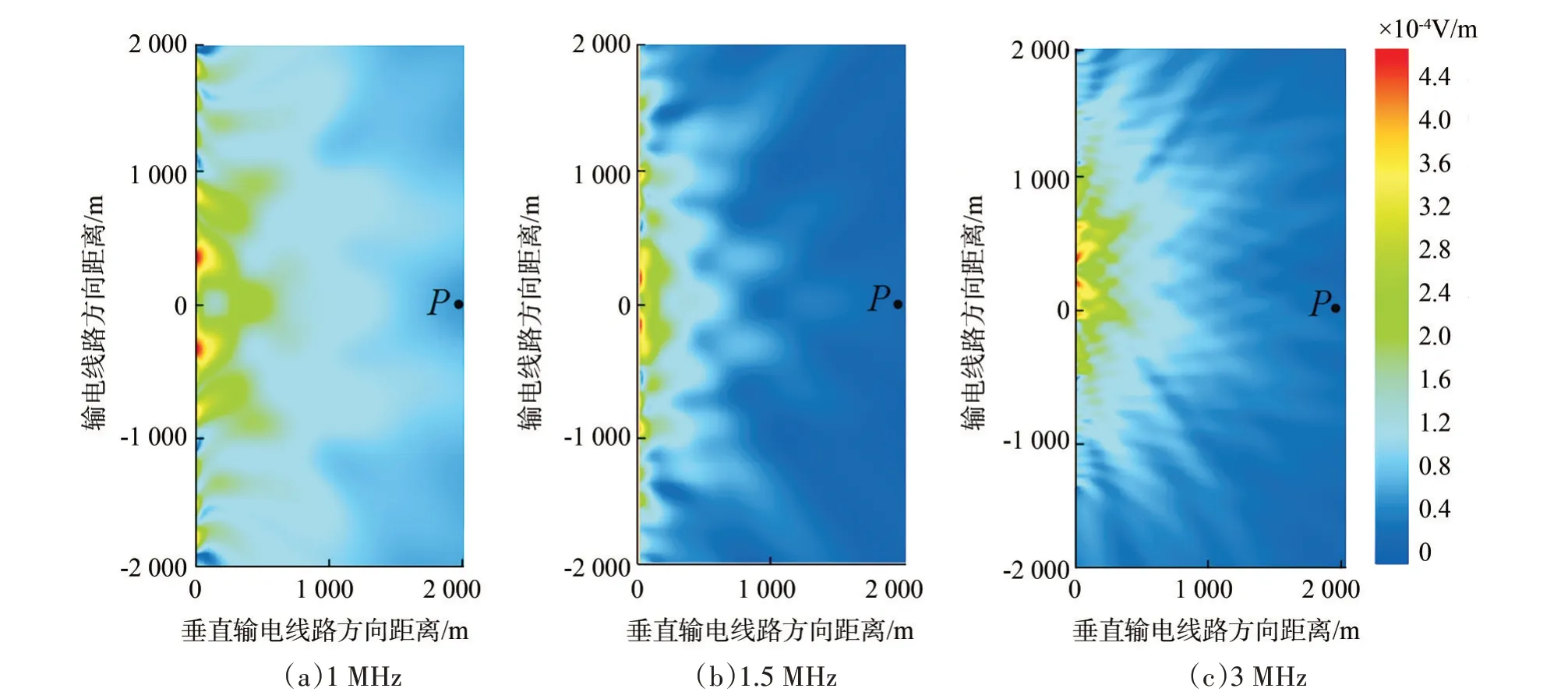
圖7 非諧振頻率下的輸電線路近場云圖Fig.7 Near-field nephogram of power transmission lines at non-resonant frequency

顯然，相同位置處，諧振頻率下的散射場強遠高于非諧振頻率下的散射場強。同時值得注意的是，越靠近輸電線路，散射場強越強，即散射場強隨空間距離的增加而衰減，該現象可由式（1）解釋。文中仿真實驗觀測點P的位置依據實際情況（輸電線路和廣播臺站的位置關系）選定。因此，本文輸電線路無源干擾諧振頻率的預測方法準確可行。

2.3.2 垂直極化平面波激勵下的無源干擾

為了驗證該方法對不同激勵的適用性，將圖2中的廣播天線替換為垂直極化平面波，入射場強為1V/m。可以發現用垂直極化平面波作為激勵時，散射場強會有所增大，但不會影響輸電線路無源干擾的諧振特性分析。選擇Q值較高的前3 個極點，其對應的參數列于表3。當與圖8 所示的矩量法結果進行比較時，前2 個諧振頻率非常一致。但第3 個諧振頻率的偏差約為0.5 MHz。

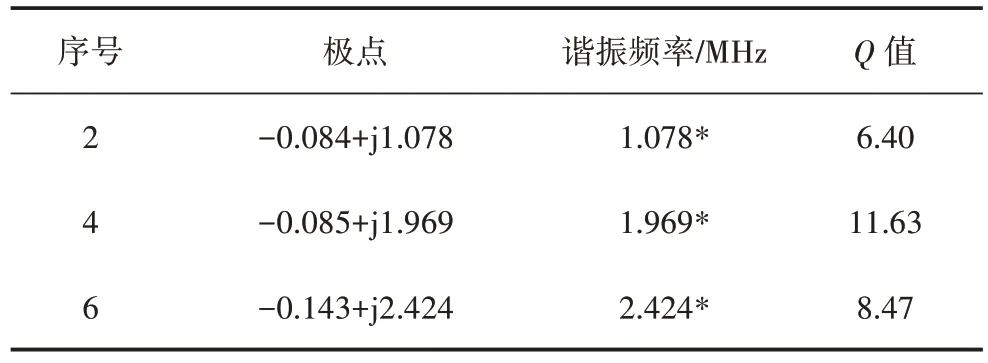
表3 前3個高Q值無源干擾諧振頻率Table 3 The first three high Q and resonance frequencies of passive interference

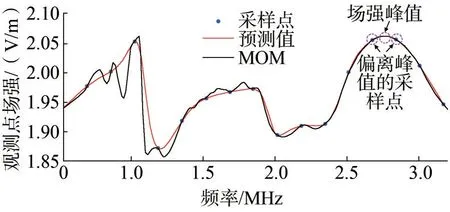
圖8 垂直極化平面波激勵下散射場強Fig.8 Scattering field strength excited by vertically polarized plane wave

通過仿真分析發現，較大的偏差主要由采樣點位置造成。由于本文采用等間隔頻率的采樣點，不可避免地獲得偏離場強峰值場強信息。若存在過多偏離峰值的采樣點，將直接導致由式（9）求解得到的系統函數的零極點發生偏移，從而使得預測的諧振頻率發生偏差。圖8 中，第3 個諧振點恰好位于兩個采樣點之間）（如紫色虛線框所示的3 個位置），直接導致偏差的出現，而前兩個諧振點沒有出現類似的情況，因而預測的諧振頻率較準確。初步建議應選擇更多的采樣點，且采樣點應盡量靠近場強較高的頻點，或者引入自適應的采樣方法。

3 結論

1）將廣義諧振理論引入到中波段輸電線路的無源干擾研究中，提出了基于廣義諧振理論的輸電線路無源干擾諧振頻率求解方法，實現了整個中波頻段的輸電線路無源干擾預測，彌補了IEEE 標準的頻率限制。仿真實驗表明，該方法不受外界激勵源的限制。當采樣點合適時，諧振頻率預測的最大偏差約為3%。

2）在獲取諧振頻率時，十分依賴構建系統函數的采樣點的位置和數量。理論上，采樣點越多，采樣點的位置越靠近真實的干擾極值，構建的系統函數越能反映系統的電磁特性，預測的諧振頻率也就越準確。但過多的采樣點，同樣會帶來較大的計算量，且干擾極值實際獲取也較為困難。因此，研究自適應的采樣方法，從而優化系統函數的構建，最終實現跟準確的無源干擾諧振頻率預測是下一步研究的重點。