24p階群的構造

陳松良,李 斌,莫貴圈

(貴州師范學院數學與大數據學院,貴州 貴陽 550018)

有限群的同構分類,一直是人們關心的問題。設p,q是不同的素數,文[1]與[2]分別確定了p3q階群和p3q2階群的構造。當p,q是不同的奇素數時,文[3]完成了p3q3階群的同構分類。文[4]分析了無三次因子階群的結構信息并給出了在同構意義上構造這類群的一個算法,文[5]對無三次因子階群的結構信息給出了更細致準確的描述和刻畫,文[6]對無四次因子階群的結構信息給出了描述和刻畫。當p>3為奇素數時,本文研究了階為24p的有限群G的同構分類,得到了G的各種互不同構的類型,從而推廣了文[7]、[8]的結果,并指出了文[7]、[8]中存在的錯誤。

在本文中,Cn表示n階循環群,Epn表示pn階初等交換群,A∶B表示群A被群B的半直積,|G|,|g|分別表示群G與元素g的階,記xg=g-1xg,其他符號的意義請讀者參看文獻[9-11]。此外,為簡化敘述,當一個群中兩個生成元交換時,在生成關系中,不再加以說明。

1 主要結果

定理1 設p是奇素數且p>3但p≠5或7,G是24p階群,那么:(i)當p≡1(mod 24)時,G共有64個互不同構的類型;(ii)當p≡13(mod 24)時,G共有61個互不同構的類型;(iii)當p≡17(mod 24)時,G共有46個互不同構的類型;(iv)當p≡11,23(mod 24)時,G共有39個互不同構的類型;(v)當p≡7,19(mod 24)但p≠7時,G共有54個互不同構的類型;(vi)當p≡5(mod 24)但p≠5時,G共有44個互不同構的類型。

2 定理1的證明

以下恒設p是奇素數且p>3但p≠5或7,G是24p階群。

引理1 不存在階為 264=24·11 的單群。

證明:見文獻[9]第78頁例5.15。

引理2 設H是24階群,則H必同構于下列15種類型之一[12]:

(a)H1=a||a|=24;

(b)H2=a,b||a|=12,|b|=2,ab=a;

(c)H3=a,b,c||a|=6,|b|=|c|=2,ab=ac=a,bc=b;

(d)H4=a,b||a|=3,|b|=8,ab=a-1;

(e)H5=a,b,c||a|=3,|b|=4,|c|=2,ab=a-1,ca=cb=c;

(f)H6=a,b,c||a|=3,|b|=2,|c|=4,ab=a-1,ca=cb=c;

(g)H7=(a:b)×c×d,其中|a|=3,|b|=|c|=|d|=2,ab=a-1;

(h)H8=a,b||a|=6,|b|=4,ba=b-1;

(i)H9=a,b,c||a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1;

(j)H10=a,b||a|=12,|b|=2,ab=a-1;

(k)H11=b,c||b|=|c|=4,b2=c2,bc=b-1×a||a|=3;

(l)H12=a,b,c||a|=3,|b|=|c|=4,b2=c2,ab=a,ac=a-1,bc=b-1;

(m)H13=a,b,c||a|=3,|b|=|c|=4,b2=c2,bc=b-1,ba=c,ca=bc;

(n)H14=a,b,c||a|=3,|b|=|c|=2,ba=c,ca=bc×d||d|=2

(o)H15=a,b,c,d||a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b.

引理3 設G是264=24·11階群,則G的 Sylow 11-子群是G的正規子群。

證明:若G的Sylow 11-子群P不正規,則由Sylow定理[10]39可知,G的Sylow 11-子群的個數是12,從而NG(P)是22階群。又由引理1知G的極小正規子群N是3階循環群或階不大于8的初等交換2-群,于是再由Sylow定理[10]39可知P?NP,因而N?NG(P)。但NG(P)是22階群,所以必有|N|=2。 由此又易知NG(P)是交換群,從而由Burnside定理[11]169知,G有正規11-補K,且顯然|K|=24。 又由引理2不難推出,任何24階群都不可能有11階的自同構,因而P只能平凡作用在K上,從而P?G,矛盾。

顯然,由Sylow定理及其推論知,當p>11時,G的Sylowp-子群P必正規。從而在本文討論的范圍內,G的Sylowp-子群P總是正規的,且G總是可解群。于是再由Schur-Zassenhaus定理[10]246知,P在G中有補子群H。顯然H是24階群,而由引理2得H有15種互不同構的類型,因此對群G可作如下討論:

引理4 設p是奇素數,且p>3但p≠5或7,σ為模p的一個原根。如果24p階群G的Sylowp-子群P=x||x|=p的補子群H是交換群:H1、H2、H3,那么:

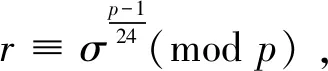
G恰有20個互不同構的類型:

G1=x||x|=24p;

G2=x×y,其中|x|=12p,|y|=2;

G3=x×y×z,其中|x|=6p,|y|=

|z|=2;

G4=x:a,其中|x|=p,|a|=24,

xa=x-1;

G5=x:a,其中|x|=p,|a|=24,

xa=xr8;

G6=x:a,其中|x|=p,|a|=24,

xa=xr6;

G7=x:a,其中|x|=p,|a|=24,

xa=xr4;

G8=x:a,其中|x|=p,|a|=24,

xa=xr3;

G9=x:a,其中|x|=p,|a|=24,

xa=xr2;

G10=x:a,其中|x|=p,|a|=24,

xa=xr;

G11=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr2;

G12=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr4;

G13=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr6;

G14=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=xr8;

G15=(x:a)×b,其中|x|=p,|a|=12,|b|=2,xa=x-1;

G16=(x:b)×a,其中|x|=p,|a|=12,|b|=2,xb=x-1;

G17=x:(a×b),其中|x|=p,|a|=12,|b|=2,xa=xr8,xb=x-1;

G18=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr4;

G19=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr8;

G20=(x:a)×b×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=x-1.

(ii) 當p≡13(mod 24)時,則G恰有18個互不同構的類型,即(i)中除了G8和G10外的其余18種構造。

(iii)當p≡17(mod 24)時,則G恰有10個互不同構的類型,即(i)中的G1、G2、G3、G4、G6、G8、G13、G15、G16、G20。

(iv)當p≡7,19(mod 24)時,則G恰有14個互不同構的類型,即(i)中除了G6、G8、G9、G10、G11和G13外的其余14種構造。

(v)當p≡5(mod 24)時,則G恰有9個互不同構的類型,即(i)中的G1、G2、G3、G4、G6、G13、G15、G16、G20。

(vi)當p≡11,23(mod 24)時,則G恰有7個互不同構的類型,即(i)中的G1、G2、G3、G4、G15、G16、G20。

證明 (i)如果G是交換群,那么容易得到G有3種互不同構的類型:G1、G2、G3。 如果G不是交換群,那么G=P∶H,且H非平凡作用在P上,即H/CH(P)同構于Aut(P)的一個非單位子群。設σ是模p的一個原根,則Aut(P)=σ是p-1階循環群,所以H/CH(P)是一個不等于1的循環群。

1)當H?H1時,CH(P)可取為a2、a3、a4、a6、a8、a12、1,由此可得G的7個互不同構的非交換群:G4、G5、…、G10。

2)當H?H2時,CH(P)可取為b、a6,b、a4,b、a3,b、a2,b、a、a3,它們分別同構于:C2、C2×C2、C3×C2?C6、C4×C2、C6×C2、C12、C4,由此可得G的7個構造:G11、G12、…、G17。 顯然,這7個群的中心互不同構,所以它們是互不同構的7個24p階群。

3)當H?H3時,CH(P)可取為b,c、a3,c、a3,b,c、a2,b,c、a,c。但b,c?C2×C2?a3,c、a3,b,c?C2×C2×C2?E8、a2,b,c?C6×C2,所以當CH(P)分別取為b,c、a3,b,c、a2,b,c時,可得G的3個互不同構的非交換群:G18、G19、G20。

如果取CH(P)=a,c,那么必有xb=x-1,于是得G的構造為:

G=(x:b)×a×c,其中|x|=p,|a|=6,|b|=|c|=2,xb=x-1。

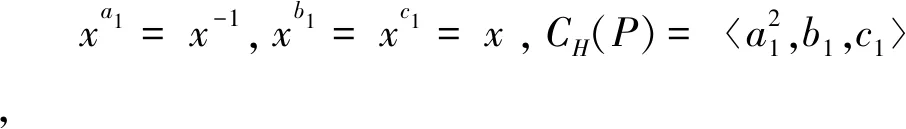
如果取CH(P)=a3,c,那么可設xa=xr8,xb=x-1,于是得G的構造為:

G=(x:(a×b))×c,其中|x|=p,|a|=6,|b|=|c|=2,xa=xr8,xb=x-1。

在上述構造中,若令a1=a5b,b1=a3,c1=c,則xa1=xr4,xb1=xc1=x,CH(P)=b1,c1,由此不難看出上述構造與G18同構。

(ii)當p≡13(mod 24)時,H/CH(P)不可能是24或8階循環群,因此這時G沒有(i)中的構造G8和G10,從而G恰有18個互不同構的類型。

(iii)當p≡17(mod 24)時,H/CH(P)不可能是24、12、6或3階循環群,因此這時G沒有(i)中的構造G5、G7、G9～G12、G14、G17、G18和G19,從而G恰有10個互不同構的類型。

(iv)當p≡7,19(mod 24)時,H/CH(P)不可能是24、12、8或4階循環群,因此這時G沒有(i)中的構造G6、G8、G9、G10、G11和G13,從而G恰有14個互不同構的類型。

(v)當p≡5(mod 24)時,H/CH(P)不可能是24、12、8、6或3階循環群,因此這時G沒有(i)中的構造G5、G7～G12、G14、G17、G18和G19,則G恰有9個互不同構的類型。

(vi)當p≡11,23(mod 24)時,H/CH(P)只可能是1或2階循環群,因此這時G沒有(i)中的構造G5～G14、G17～G19,則G恰有7個互不同構的類型。

引理5 設p是奇素數,且p>3但p≠5或7,σ為模p的一個原根。 如果24p階群G的Sylowp-子群P=x||x|=p的補子群H是非交換群:H4、H5、H6、H7,那么:

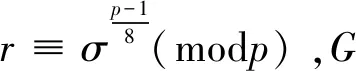
G1=x×(a:b),其中|x|=p,|a|=3,|b|=8,ab=a-1;

G2=x×(a:b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1;

G3=x×(a:b)×c,其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1;

G4=x×(a:b)×c×d,其中

|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1;

G5=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=xr;

G6=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=xr2;

G7=(x×a):b,其中|x|=p,|a|=3,|b|=8,ab=a-1,xb=x-1;

G8=((x×a):b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,xb=xr2;

G9=((x×a):b)×c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,xb=x-1;

G10=(x:c)×(a:b),其中|x|=p,

|a|=3,|b|=4,|c|=2,ab=a-1,xc=x-1;

G11=((x×a):b)×c,其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1,xb=x-1;

G12=(x:c)×(a:b),其中|x|=p,

|a|=3,|b|=2,|c|=4,ab=a-1,xc=xr2;

G13=(x:c)×(a:b),其中|x|=p,

|a|=3,|b|=2,|c|=4,ab=a-1,xc=x-1;

G14=(x×a):(b×c),其中|x|=p,|a|=3,|b|=2,|c|=4,ab=a-1,ac=a,xb=xc=x-1;

G15=((x×a):b)×c×d,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1,xb=x-1;

G16=(x:d)×(a:b)×c,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ab=a-1,xd=x-1.

(ii)當p≡5,13(mod 24)時,則G恰有15個互不同構的類型,即(i)中除了G5外的其余15種構造。

(iii)當p≡7,11,19,23(mod 24)時,則G恰有12個互不同構的類型,即(i)中的G1、G2、G3、G4、G7、G9、G10、G11、G13、G14、G15、G16。

證明 (i)如果H平凡作用在群P上,那么容易得到G有4種互不同構的類型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,即H/CH(P)同構于Aut(P)的一個非單位子群。設σ是模p的一個原根,則Aut(P)=σ是p-1階循環群,所以H/CH(P)是一個不等于1的循環群。

1)當H?H4時,CH(P)可取為a、a,b4、a,b2,由此可得G的3個互不同構的構造:G5、G6、G7。

2)當H?H5時,CH(P)可取為a,c、a,b2,c、a,b,且易知a,c?C6、a,b2,c?C6×C2、a,b?C3:C4是非交換群。 于是a,c、a,b2,c、a,b是兩兩互不同構的,從而得G的3個互不同構的構造:G8、G9、G10。

3)當H?H6時,CH(P)可取為a,c、a,b、a,b,c2、a,bc,且易知a,c?C12、a,b?C3:C2?S3、a,b,c2?S3×C2、a,bc?C3:C4。 于是a,c、a,b、a,b,c2、a,bc是兩兩互不同構的,從而得G的4個互不同構的構造:G11、G12、G13、G14。

4)當H?H7時,CH(P)可取為a,c,d、a,b,c,而a,c,d?C6×C2,a,b,c?S3×C2,由此可得G的2個互不同構的構造:G15、G16。

(ii)當p≡5,13(mod 24)時,H/CH(P)不可能是8階循環群,因此這時G沒有(i)中的構造G5,從而G恰有15個互不同構的類型。

(iii)當p≡7,11,19,23(mod 24)時,H/CH(P)不可能是8階或4階循環群,因此這時G沒有(i)中的構造G5、G6、G8、G12,從而G恰有12個互不同構的類型。

引理6 設p是奇素數,且p>3但p≠5或7,σ為模p的一個原根。如果24p階群G的Sylowp-子群P=x||x|=p的補子群H是非交換群:H8、H11、H13、H14,那么:

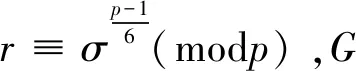
G1=x×a×b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,bc=b-1;

G2=x×a×b,c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1;

G3=x×(b,c:a),|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ba=c,ca=bc;

G4=x×((b×c):a)×d,其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc;

G5=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=xr,ba=b-1;

G6=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=xr2,ba=b-1;

G7=(x×b):a,其中|x|=p,|a|=6,|b|=4,xa=x-1,ba=b-1;

G8=x:(b:a),其中|x|=p,|a|=6,|b|=4,ba=b-1,xa=x,xb=x-1;

G9=x:(b:a),其中|x|=p,|a|=6,|b|=4,ba=b-1,xa=xr2,xb=x-1;

G10=x:(a×b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,xa=xr2,xb=x,xc=x-1;

G11=(x:a)×b,c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,xa=xr2;

G12=(x×a×b):c,其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,xc=x-1,ac=a,bc=b-1;

G13=(x×b,c):a,其中|x|=p,|a|=3,|b|=2,|c|=4,b2=c2,bc=b-1,xa=xr2,ba=b,ca=c;

G14=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xr2,xb=xc=x,xd=x-1;

G15=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xr2,xb=xc=xd=x;

G16=x:(((b×c):a)×d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,xa=xb=xc=x,xd=x-1.

(ii)當p≡5,11,17,23(mod 24)時,則G恰有8個互不同構的類型,即(i)中的G1、G2、G3、G4、G7、G8、G12、G16。

證明 (i)如果H平凡作用在群P上,那么容易得到G有4種互不同構的類型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,即H/CH(P)同構于Aut(P)的一個非單位子群。設σ是模p的一個原根,則Aut(P)=σ是p-1階循環群,所以H/CH(P)是一個不等于1的循環群。

1)當H?H8時,為了使H/CH(P)成為非單位的循環群,只要CH(P)取為b、a2,b、a3,b、a,b2、a3,b2。 不難看出這5個群是互不同構的,所以由此可得G的5個互不同構的構造:G5、G6、G7、G8、G9。

2)當H?H11時,CH(P)取為b、b,c、a,b,可使H/CH(P)分別為6,3,2階循環群,從而得G的3個互不同構的構造:G10、G11、G12。

3)當H?H13時,CH(P)只能取為b,c,使H/CH(P)是一個3階循環群,從而得G的構造:G13。

4)當H?H14時,CH(P)取為b,c、b,c,d、a,b,c可使H/CH(P)分別為6,3,2階循環群,由此得G的3個不同構的構造:G14、G15、G16。

(ii)當p≡5,11,17,23(mod 24)時,H/CH(P)只可能是2階循環群,因此這時G沒有(i)中的構造G5、G6、G9、G10、G11、G13、G14、G15,從而G恰有8個互不同構的類型。

引理7 設p是奇素數,且p>3但p≠5或7。如果24p階群G的Sylowp-子群P=x||x|=p的補子群H是非交換群:H9、H10、H12、H15,那么G恰有12個互不同構的類型:

G1=x×(a:b,c),其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1;

G2=x×(a:b),其中|x|=p,|a|=12,|b|=2,ab=a-1;

G3=x×(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1;

G4=x×(((b×c):a):d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b;

G5=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x,xc=x-1;

G6=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x-1,xc=x;

G7=(x×a):b,c,其中|x|=p,|a|=3,|b|=4,|c|=2,ab=a-1,ac=a,bc=b-1,xb=x-1,xc=x-1;

G8=(x×a):b,其中|x|=p,|a|=12,|b|=2,ab=a-1,xb=x-1;

G9=x:(a:b),其中|x|=p,|a|=12,|b|=2,ab=a-1,xa=x-1,xb=x;

G10=x:(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1,xa=xb=x,xc=x-1;

G11=x:(a:b,c),其中|x|=p,|a|=3,|b|=|c|=4,b2=c2,bc=b-1,ab=a,ac=b-1,xa=xc=x,xb=x-1;

G12=x:(((b×c):a):d),其中|x|=p,|a|=3,|b|=|c|=|d|=2,ba=c,ca=bc,ad=a-1,bd=c,cd=b,xa=xb=xc=x,xd=x-1.

證明 如果H平凡作用在群P上,那么容易得到G有4種互不同構的類型:G1、G2、G3、G4。 如果H非平凡作用在群P上,那么G=P∶H,且H/CH(P)同構于Aut(P)的一個2階循環群。

1)當H?H9時,CH(P)可取為a,b、a,b2,c或a,b2,bc,從而可得G的3種構造:G5、G6、G7。 由于a,b?C3:C4、a,b2,c?C3×C2×C2、a,b2,bc?(C3:C2)×C2,所以a,b、a,b2,c與a,b2,bc兩兩互不同構的,故G5、G6、G7是3個互不同構的24p階群。

2)當H?H10時,CH(P)取為a、a2,b、a2,ab,可使H/CH(P)為2階循環群。令CH(P)=a或a2,b,分別得G的2個互不同構的構造:G8、G9。 若令CH(P)=a2,ab,則因為ab與b在H10中的地位是相同的,因而所得到的群G與G9同構。

3)當H?H12時,CH(P)可為a,b或a,c。 又a,b和a,c是不同構的,因而得G的2個不同構的構造:G10、G11。

4)當H?H15時,CH(P)只有取為a,b,c才能使H/CH(P)為2階循環群,由此得G的構造:G12。

由引理4至引理7,易知定理1成立。

注:必須指出,文[7]中引理2遺漏了兩種不同的類型,引理3的表述不對,證明過程是不嚴謹的;文[8]中引理2和3的證明存在錯誤。[7]中引理2的正確表述是:當Sylow 7-子群正規時,168階群共有54種互不同構的類型(在本文的引理4至7中,令p=7即得);[7]中引理3的正確表述是:當Sylow 7-子群不正規時,168階群只有3種互不同構的類型,其中僅有一種是不可解的,另外兩種分別是Sylow 3-子群與Sylow 2-子群都正規時的1種和 Sylow 3-子群不正規而Sylow 2-子群正規時的1種(限于篇幅,我們在此不再詳證此結論)。